Спиновая волна

Эта статья включает список общих ссылок , но в ней отсутствуют соответствующие встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Декабрь 2013 ) ( Узнайте, как и когда удалять это сообщение )

В физике конденсированного состояния спиновая волна представляет собой распространяющееся возмущение в упорядочении магнитного материала. Эти низколежащие коллективные возбуждения возникают в магнитных решетках с непрерывной симметрией . С эквивалентной квазичастичной точки зрения спиновые волны известны как магноны , которые являются бозонными модами спиновой решетки , которые примерно соответствуют фононным возбуждениям ядерной решетки. При повышении температуры тепловое возбуждение спиновых волн уменьшает спонтанную намагниченность ферромагнетика . Энергии спиновых волн обычно составляют всего мкэВ в соответствии с типичными точками Кюри при комнатной температуре и ниже.

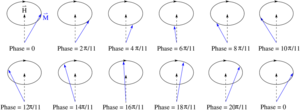
Самый простой способ понять спиновые волны — рассмотреть гамильтониан для ферромагнетика Гейзенберга :${\displaystyle {\mathcal {H}}}$

${\displaystyle {\mathcal {H}}=-{\frac {1}{2}}J\sum _{i,j}\mathbf {S} _{i} \cdot \mathbf {S} _{j}-g\mu _ {\rm {B}}\sum _{i}\mathbf {H} \cdot \mathbf {S} _{i}}$

где J - обменная энергия , операторы S представляют спины в точках решетки Бравэ , g - g -фактор Ланде , μ _B - магнетон Бора , а H - внутреннее поле, которое включает внешнее поле плюс любое "молекулярное" поле. Обратите внимание, что в классическом случае континуума и в 1 + 1 измерениях уравнение ферромагнетика Гейзенберга имеет вид

${\displaystyle \mathbf {S} _{t}=\mathbf {S} \times \mathbf {S} _{xx}.}$

В измерениях 1 + 1, 2 + 1 и 3 + 1 это уравнение допускает несколько интегрируемых и неинтегрируемых расширений, таких как уравнение Ландау-Лифшица , уравнение Ишимори и т. д. Для ферромагнетика J > 0 и основное состояние гамильтониана — это то, в котором все спины выровнены параллельно полю H. Это собственное состояние можно проверить, переписав его в терминах операторов повышения и понижения спина, заданных как:${\displaystyle |0\rangle }$${\displaystyle |0\rangle }$${\displaystyle {\mathcal {H}}}$

${\displaystyle S^{\pm }=S^{x}\pm iS^{y}}$

в результате чего

${\displaystyle {\mathcal {H}}=-{\frac {1}{2}}J\sum _{i,j}S_{i}^{z}S_{j}^{z}-g\mu _{\rm {B}}H\sum _{i}S_{i}^{z}-{\frac {1}{4}}J\sum _{i,j}(S_{i}^{+}S_{j}^{-}+S_{i}^{-}S_{j}^{+})}$

где z было взято как направление магнитного поля. Оператор понижения спина S ⁻ уничтожает состояние с минимальной проекцией спина вдоль оси z , в то время как оператор повышения спина S ⁺ уничтожает основное состояние с максимальной проекцией спина вдоль оси z . Поскольку

${\displaystyle S_{i}^{z}|0\rangle =s|0\rangle }$

для максимально выровненного состояния мы находим

${\displaystyle {\mathcal {H}}|0\rangle =\left(-Js^{2}-g\mu _{\rm {B}}Hs\right)N|0\rangle }$

где N — общее число узлов решетки Бравэ. Подтверждено предположение о том, что основное состояние является собственным состоянием гамильтониана.

Можно предположить, что первое возбужденное состояние гамильтониана имеет один случайно выбранный спин в позиции i, повернутый таким образом, что

${\displaystyle S_{i}^{z}|1\rangle =(s-1)|1\rangle,}$

но на самом деле это расположение спинов не является собственным состоянием. Причина в том, что такое состояние преобразуется операторами повышения и понижения спина. Оператор увеличит z -проекцию спина в позиции i обратно к его низкоэнергетической ориентации, но оператор понизит z -проекцию спина в позиции j . Таким образом, объединенный эффект двух операторов заключается в распространении повернутого спина в новое положение, что является намеком на то, что правильное собственное состояние - это спиновая волна , а именно суперпозиция состояний с одним уменьшенным спином. Штраф обменной энергии, связанный с изменением ориентации одного спина, уменьшается за счет распространения возмущения по большой длине волны. Степень разориентации любых двух близкорасположенных спинов тем самым минимизируется. Из этого объяснения можно понять, почему модель магнита Изинга с дискретной симметрией не имеет спиновых волн: понятие распространения возмущения в спиновой решетке по большой длине волны не имеет смысла, когда спины имеют только две возможные ориентации. Существование низкоэнергетических возбуждений связано с тем, что в отсутствие внешнего поля спиновая система имеет бесконечное число вырожденных основных состояний с бесконечно мало различающимися ориентациями спина. Существование этих основных состояний можно увидеть из того факта, что состояние не имеет полной вращательной симметрии гамильтониана , явление, которое называется спонтанным нарушением симметрии .${\displaystyle S_{i}^{+}}$${\displaystyle S_{j}^{-}}$${\displaystyle |0\rangle }$${\displaystyle {\mathcal {H}}}$

В этой модели намагничивание

${\displaystyle M={\frac {N\mu _{\rm {B}}gs}{V}}}$

где V — объем. Распространение спиновых волн описывается уравнением движения Ландау-Лифшица:

${\displaystyle {\frac {d\mathbf {M} }{dt}}=-\gamma \mathbf {M} \times \mathbf {H} - {\frac {\lambda \mathbf {M} \times (\mathbf {M} \times \mathbf {H})}{M^{2}}}}$

где γ — гиромагнитное отношение, а λ — константа затухания. Перекрестные произведения в этом устрашающе выглядящем уравнении показывают, что распространение спиновых волн регулируется моментами, создаваемыми внутренними и внешними полями. (Эквивалентной формой является уравнение Ландау-Лифшица-Гильберта , которое заменяет последний член на более «просто выглядящий» эквивалентный.)

Первый член в правой части уравнения описывает прецессию намагниченности под влиянием приложенного поля, тогда как вышеупомянутый последний член описывает, как вектор намагниченности «закручивается» по спирали к направлению поля с течением времени. В металлах силы затухания, описываемые константой λ, во многих случаях определяются вихревыми токами.

Одно важное различие между фононами и магнонами заключается в их дисперсионных соотношениях . Дисперсионное соотношение для фононов является линейным в первом порядке по волновому вектору k , а именно ώ = ck , где ω — частота, а c — скорость звука. Магноны имеют параболическое дисперсионное соотношение: ώ = Ak ² , где параметр A представляет собой « спиновую жесткость ». Форма k ² является третьим членом разложения Тейлора косинусного члена в выражении энергии, происходящем от скалярного произведения S _i ⋅ S _j . Основная причина различия в дисперсионных соотношениях заключается в том, что параметр порядка (намагниченность) для основного состояния в ферромагнетиках нарушает симметрию обращения времени . Два соседних спина в твердом теле с постоянной решетки a , которые участвуют в моде с волновым вектором k, имеют угол между ними, равный ka .

Спиновые волны наблюдаются четырьмя экспериментальными методами: неупругое рассеяние нейтронов , неупругое рассеяние света ( рассеяние Мандельштама — Бриллюэна , комбинационное рассеяние и неупругое рассеяние рентгеновских лучей ), неупругое рассеяние электронов ( спектроскопия потерь энергии электронов со спиновым разрешением ) и спин-волновой резонанс ( ферромагнитный резонанс ).

• При неупругом рассеянии нейтронов измеряется потеря энергии пучка нейтронов, возбуждающих магнон, как правило, как функция вектора рассеяния (или эквивалентно переданному импульсу), температуры и внешнего магнитного поля. Измерения неупругого рассеяния нейтронов могут определить дисперсионную кривую для магнонов так же, как и для фононов . Важные объекты неупругого рассеяния нейтронов присутствуют в источнике нейтронов ISIS в Оксфордшире, Великобритания, в Институте Лауэ-Ланжевена в Гренобле , Франция, в высокопоточном изотопном реакторе в Национальной лаборатории Оук-Ридж в Теннесси, США, и в Национальном институте стандартов и технологий в Мэриленде, США.
• Рассеяние Бриллюэна аналогичным образом измеряет потерю энергии фотонов (обычно на удобной видимой длине волны), отраженных от магнитного материала или прошедших через него. Спектроскопия Бриллюэна похожа на более широко известное рассеяние Рамана , но исследует более низкую энергию и имеет превосходное энергетическое разрешение, чтобы иметь возможность обнаружить энергию магнонов в мэВ.
• Ферромагнитный (или антиферромагнитный) резонанс вместо этого измеряет поглощение микроволн , падающих на магнитный материал, спиновыми волнами, как правило, как функцию угла, температуры и приложенного поля. Ферромагнитный резонанс является удобным лабораторным методом для определения влияния магнитокристаллической анизотропии на дисперсию спиновых волн. Одна группа в Институте физики микроструктур Макса Планка в Галле, Германия, доказала, что с помощью спектроскопии потери энергии спин-поляризованных электронов (SPEELS) можно возбуждать поверхностные магноны очень высокой энергии. Эта техника позволяет исследовать дисперсию магнонов в сверхтонких ферромагнитных пленках. Первый эксперимент был проведен для пленки Fe толщиной 5 ML. ^[1] С разрешением по импульсу дисперсия магнонов была исследована для пленки fcc Co толщиной 8 ML на Cu(001) и пленки hcp Co толщиной 8 ML на W(110) соответственно. ^[2] Максимальная энергия магнонов на границе поверхностной зоны Бриллюэна составила 240 мэВ.

При работе магнитоэлектронных устройств на высоких частотах генерация спиновых волн может быть важным механизмом потери энергии. Генерация спиновых волн ограничивает ширину линий и, следовательно, добротность Q ферритовых компонентов , используемых в микроволновых устройствах. Обратная величина наименьшей частоты характерных спиновых волн магнитного материала дает временную шкалу для переключения устройства на основе этого материала.

• Магноника
• Преобразование Гольштейна – Примакова.
• Спиновая инженерия

• Спиновые волны - Фейнмановские лекции по физике
• Список лабораторий, выполняющих измерения рассеяния Мандельштама-Бриллюэна.