Электрофоретическое рассеяние света

Для проверки этой статьи нужны дополнительные цитаты . Помогите улучшить эту статью , добавив ссылки на надежные источники . Материалы без ссылок могут быть оспорены и удалены. Найти источники:  "Электрофоретическое рассеяние света" – новости  · газеты  · книги  · ученый  · JSTOR ( сентябрь 2017 г. ) ( Узнайте, как и когда удалять это сообщение )

Электрофоретическое рассеяние света (также известное как лазерный доплеровский электрофорез и фазовый анализ рассеяния света ) основано на динамическом рассеянии света . Сдвиг частоты или фазовый сдвиг падающего лазерного луча зависит от подвижности диспергированных частиц . При динамическом рассеянии света броуновское движение вызывает движение частиц. При электрофоретическом рассеянии света эту функцию выполняет осциллирующее электрическое поле .

Метод используется для измерения электрофоретической подвижности , из которой затем можно рассчитать дзета-потенциал . Приборы для применения метода имеются в продаже у нескольких производителей. Последний набор расчетов требует информации о вязкости и диэлектрической проницаемости дисперсионной среды ; также требуется соответствующая теория электрофореза . Разбавление образца часто необходимо для устранения многократного рассеяния падающего лазерного луча и/или взаимодействия частиц.

Лазерный луч проходит через ячейку электрофореза, облучает диспергированные в ней частицы и рассеивается частицами. Рассеянный свет обнаруживается фотоумножителем после прохождения через два отверстия. Существует два типа оптических систем: гетеродинная и полосатая. Уэр и Флайгар ^[1] разработали прибор ELS гетеродинного типа, который был первым прибором этого типа. В приборе ELS с полосатой оптикой ^[2] лазерный луч разделяется на два луча. Они пересекаются внутри ячейки электрофореза под фиксированным углом, создавая рисунок полос. Рассеянный свет от частиц, который мигрирует внутри полосы, модулируется по интенсивности. Частотные сдвиги от обоих типов оптики подчиняются одним и тем же уравнениям. Наблюдаемые спектры похожи друг на друга. Ока и др. разработали прибор ELS с оптикой гетеродинного типа ^[3] , который теперь доступен в продаже. Его оптика показана на рис. 3.

Если частоты пересекающихся лазерных лучей одинаковы, то невозможно определить направление движения мигрирующих частиц. Вместо этого можно определить только величину скорости (т. е. скорость). Следовательно, знак дзета-потенциала не может быть установлен. Это ограничение можно преодолеть, сдвинув частоту одного из лучей относительно другого. Такое смещение можно назвать частотной модуляцией или, более разговорно, просто модуляцией. Модуляторы, используемые в ELS, могут включать пьезоэлектрические зеркала или акустооптические модуляторы. Эта схема модуляции также используется в методе гетеродинного рассеяния света.

Фазовый анализ рассеяния света (PALS) — это метод оценки дзета-потенциала, в котором анализируется скорость изменения фазы интерференции между светом, рассеянным образцом, и модулированным опорным лучом. Эта скорость сравнивается с математически сгенерированной синусоидой, предопределенной частотой модулятора. ^[4] Применение больших полей, которые могут привести к нагреву образца и разрушению коллоидов, больше не требуется. Но любая нелинейность модулятора или любое изменение характеристик модулятора со временем будет означать, что сгенерированная синусоида больше не будет отражать реальные условия, и полученные измерения дзета-потенциала станут менее надежными.

Дальнейшим развитием техники PALS является так называемая техника «непрерывно контролируемого PALS» (cmPALS), которая решает проблему нелинейности модуляторов. Дополнительный модулятор обнаруживает интерференцию между модулированным и немодулированным лазерным светом. Таким образом, его частота биений является исключительно частотой модуляции и, следовательно, не зависит от электрофоретического движения частиц. Это приводит к более быстрым измерениям, более высокой воспроизводимости даже при низких приложенных электрических полях, а также более высокой чувствительности измерения. ^[5]

Частота света, рассеянного частицами, подвергающимися электрофорезу, смещена на величину эффекта Доплера относительно частоты падающего света, : . Сдвиг может быть обнаружен с помощью гетеродинной оптики, в которой рассеиваемый свет смешивается с опорным светом. Автокорреляционная функция интенсивности смешанного света, , может быть приближенно описана следующей затухающей косинусоидальной функцией [7].${\displaystyle \upsilon _{D}\,}$${\displaystyle \upsilon \,}$${\displaystyle g(\тау)\,}$

${\displaystyle g(\tau )=A+B\exp(-\Gamma \tau )\cos(2\pi \upsilon _{o})+C\exp(-2\Gamma \tau )\,\qquad (1)}$

где — константа распада, а A, B и C — положительные константы, зависящие от оптической системы.${\displaystyle \Гамма \,}$

Частота затухания — это наблюдаемая частота, представляющая собой разницу частот между рассеянным и опорным светом.${\displaystyle \upsilon _{o}\,}$

${\displaystyle \upsilon _{o}=|\upsilon _{s}-\upsilon _{r}|=|(\upsilon _{i}+\upsilon _{D})-(\upsilon _{i} +\upsilon _{M})|\qquad (2)}$

где — частота рассеянного света, частота опорного света, частота падающего света (лазерного света) и частота модуляции.${\displaystyle \upsilon _{s}\,}$${\displaystyle \upsilon _{r}\,}$${\displaystyle \upsilon _{i}\,}$${\displaystyle \upsilon _{M}\,}$

Спектр мощности смешанного света, а именно преобразование Фурье , дает пару функций Лоренца, имеющих полуширину на половине максимума.${\displaystyle g(\тау)\,}$${\displaystyle \pm \Delta \upsilon \,}$${\displaystyle \Gamma /2\pi \,}$

В дополнение к этим двум, последний член в уравнении (1) дает еще одну функцию Лоренца при${\displaystyle \upsilon =0\,}$

Доплеровский сдвиг частоты и постоянная затухания зависят от геометрии оптической системы и выражаются соответственно уравнениями.

${\displaystyle \upsilon _{D}={\frac {Vq}{2\pi }}\qquad (3)}$

и

${\displaystyle \Гамма =D|q|^{2}\qquad (4)}$

где — скорость частиц, — амплитуда вектора рассеяния, — константа поступательной диффузии частиц.${\displaystyle \ V\,}$${\displaystyle \ д\,}$${\displaystyle \ D\,}$

Амплитуда вектора рассеяния определяется уравнением${\displaystyle \ д\,}$

${\displaystyle \ |q|={\frac {4\pi n}{\lambda _{0}}}\sin \left({\frac {\theta }{2}}\right)\qquad (5)}$

Поскольку скорость пропорциональна приложенному электрическому полю, кажущаяся электрофоретическая подвижность определяется уравнением${\displaystyle \ V\,}$${\displaystyle \ E\,}$${\displaystyle \ \mu _{obs}\,}$

${\displaystyle \ {\vec {V}}=\mu _{obs}{\vec {E}}\qquad (6)}$

Наконец, связь между частотой доплеровского сдвига и подвижностью дается для случая оптической конфигурации рис. 3 уравнением

${\displaystyle \upsilon _{D}=\mu _{obs}{\frac {nE}{\lambda _{0}}}\sin \theta \qquad (7)}$

где - напряженность электрического поля, показатель преломления среды, , длина волны падающего света в вакууме и угол рассеяния. Знак является результатом векторного расчета и зависит от геометрии оптики.${\displaystyle \ E\,}$${\displaystyle \ н\,}$${\displaystyle \ \lambda _{0}\,}$${\displaystyle \ \тета \,}$${\displaystyle \ v_{D}\,}$

Спектральную частоту можно получить по уравнению (2). Когда , уравнение (2) модифицируется и выражается как${\displaystyle \ |\upsilon _{M}|>|\upsilon _{D}|\,}$

${\displaystyle \upsilon _{p}=\upsilon _{o}=\pm (\upsilon _{D}-|\upsilon _{M}|)\qquad (8)}$

Частоту модуляции можно получить как частоту затухания без приложения электрического поля.${\displaystyle \upsilon _{M}\,}$

Диаметр частицы получается, если предположить, что частица имеет сферическую форму. Это называется гидродинамическим диаметром, .${\displaystyle \ d_{H}\,}$

${\displaystyle \ d_{H}={\frac {k_{B}T}{3\pi \eta D}}\qquad (10)}$

где — коэффициент Больцмана , — абсолютная температура, — динамическая вязкость окружающей жидкости.${\displaystyle \ k_{B}\,}$${\displaystyle \ Т\,}$${\displaystyle \ \эта \,}$

На рисунке 4 показаны два примера гетеродинных автокорреляционных функций рассеянного света от раствора сульфата полистирола натрия (NaPSS; MW 400 000; 4 мг/мл в 10 мМ NaCl). Осциллирующая корреляционная функция, показанная на рисунке 4a, является результатом интерференции между рассеянным светом и модулированным опорным светом. Биение на рисунке 4b дополнительно включает вклад от изменений частоты света, рассеянного молекулами PSS под действием электрического поля 40 В/см.

На рисунке 5 показаны спектры мощности гетеродина, полученные с помощью преобразования Фурье автокорреляционных функций, показанных на рисунке 4.

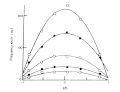
На рисунке 6 показаны графики частот доплеровского сдвига, измеренные на различной глубине ячейки и напряженности электрического поля, где образцом является раствор NaPSS. Эти параболические кривые называются профилями электроосмотического потока и указывают на то, что скорость частиц изменяется на разной глубине. Поверхностный потенциал стенки клетки создает электроосмотический поток. Поскольку камера для электрофореза представляет собой закрытую систему, в центре ячейки создается обратный поток. Тогда наблюдаемая подвижность или скорость из уравнения (7) является результатом комбинации осмотического потока и электрофоретического движения.

Анализ электрофоретической подвижности изучался Мори и Окамото [16], которые учли эффект электроосмотического потока на боковой стенке.

Профиль скорости или подвижности в центре ячейки приблизительно задается уравнением (11) для случая, когда k>5.

${\displaystyle \ U_{a}(z)=AU_{0}(z/b)^{2}+\Delta U_{0}(z/b)+(1-A)U_{0}+U_{ p}\qquad (11)}$

где

${\displaystyle \ z=\,}$ глубина ячейки

${\displaystyle \ U_{a}(z)=\,}$ кажущаяся электрофоретическая скорость частицы в позиции z.

${\displaystyle \ U_{p}=\,}$ истинная электрофоретическая скорость частиц.

${\displaystyle \ z/b=\,}$толщина ячейки

${\displaystyle \ U_{0}=\,}$средняя скорость осмотического потока в верхней и нижней стенке клетки.

${\displaystyle \Delta U_{0}=\,}$разница между скоростями осмотического потока в верхней и нижней стенке клетки.

${\displaystyle \ A={\frac {1}{(2/3)-(0.420166/k)}}\qquad (12)}$

${\displaystyle \ k=a/b\,}$, отношение длин двух сторон прямоугольного поперечного сечения.

Параболическая кривая сдвига частоты, вызванного электроосмотическим потоком, показанная на рис. 6, соответствует уравнению (11) с применением метода наименьших квадратов.

Поскольку подвижность пропорциональна сдвигу частоты света, рассеянного частицей, и скорости перемещения частицы, как указано в уравнении (7), все сдвиги скорости, подвижности и частоты выражаются параболическими уравнениями. Тогда была получена истинная электрофоретическая подвижность частицы, электроосмотическая подвижность на верхней и нижней стенках клетки. Сдвиг частоты, вызванный только электрофорезом частиц, равен кажущейся подвижности на неподвижном слое.

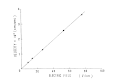
Скорость электрофоретической миграции, полученная таким образом, пропорциональна электрическому полю, как показано на рис. 7. Сдвиг частоты увеличивается с увеличением угла рассеяния, как показано на рис. 8. Этот результат согласуется с теоретическим уравнением (7).

• 
  Рис.4 а и б; Корреляционная функция с электрическим полем и без него. Образец: раствор NaPSS (молекулярная масса: 400 000) 4 мг/мл в 10 мМ NaCl. Приложенное электрическое поле: (а) 0 В/см; (б) 40 В/см. Угол рассеяния 7,0 градусов, температура 25 +-0,3
• 
  Рис. 5. Спектры мощности гетеродина, полученные с помощью БПФ корреляционных функций.
• 
  Рис. 6. Частотные сдвиги, наблюдаемые на различной глубине ячеек.
• 
  Рис. 7. Зависимость скорости от электрического поля в неподвижном слое.
• 
  Рис. 8. Сдвиг частоты в зависимости от угла рассеяния.

Электрофоретическое рассеяние света (ELS) в основном используется для характеристики поверхностных зарядов коллоидных частиц , таких как макромолекулы или синтетические полимеры (например, полистирол ^[6] ) в жидких средах в электрическом поле. В дополнение к информации о поверхностных зарядах, ELS также может измерять размер частиц белков ^[7] и определять распределение дзета-потенциала .

ELS полезен для характеристики информации о поверхности белков. Уэр и Флайгар (1971) продемонстрировали, что электрофоретические методы можно комбинировать с лазерной спектроскопией биений, чтобы одновременно определять электрофоретическую подвижность и коэффициент диффузии бычьего сывороточного альбумина . ^[8] Ширина спектра света с допплеровским сдвигом , который рассеивается из раствора макромолекул, пропорциональна коэффициенту диффузии . ^[9] Допплеровский сдвиг пропорционален электрофоретической подвижности макромолекулы. ^[10] Из исследований, в которых этот метод применялся к поли (L-лизину) , считается, что ELS контролирует подвижности флуктуаций в присутствии растворителей с различными концентрациями солей. ^[11] Также было показано, что данные об электрофоретической подвижности можно преобразовать в значения дзета-потенциала , что позволяет определять изоэлектрическую точку белков и количество электрокинетических зарядов на поверхности. ^[12]

Другие биологические макромолекулы, которые можно анализировать с помощью ELS, включают полисахариды . Значения pKa хитозанов можно рассчитать из зависимости значений электрофоретической подвижности от pH и плотности заряда. ^[13] Как и белки, размер и дзета-потенциал хитозанов можно определить с помощью ELS. ^[14]

ELS также применялся к нуклеиновым кислотам и вирусам. Метод может быть расширен для измерения электрофоретической подвижности крупных молекул бактерий при низкой ионной силе. ^[15]

Метод ELS использовался для характеристики полидисперсности , нанодисперсности и стабильности однослойных углеродных нанотрубок в водной среде с поверхностно-активными веществами. ^{[ необходима ссылка ]} Метод можно использовать в сочетании с динамическим рассеянием света для измерения этих свойств нанотрубок во многих различных растворителях.

(1) Surfactant Science Series, редактор-консультант Martin J. Schick Consultant New York, том 76 Электрические явления на интерфейсах Второе издание, Основы, измерения и приложения, второе издание, исправленное и расширенное. Под ред. Хироюки Ошимы, Кунио Фурусавы. 1998. К. Ока и К. Фурусава, Глава 8 Электрофорез, стр. 152–223. Marcel Dekker, Inc.,

(7) BR Ware и DD Haas, в книге «Быстрый метод в физической биохимии и клеточной биологии» (под ред. RI Sha'afi и SM Fernandez), Elsevier, Нью-Йорк, 1983, гл. 8.

(9) Ware, BR; Flygare, WH (1972). «Рассеяние света в смесях BSA, димеров BSA и фибриногена под влиянием электрических полей». Журнал коллоидной и интерфейсной науки . 39 (3). Elsevier BV: 670–675. doi :10.1016/0021-9797(72)90075-6. ISSN  0021-9797.

(10) Йозефович, Дж.; Халлетт, Ф. Р. (1975-03-01). «Гомодинное электрофоретическое рассеяние света сферами полистирола с помощью корреляции интенсивности поперечного лазерного луча». Прикладная оптика . 14 (3). Оптическое общество: 740–742. doi :10.1364/ao.14.000740. ISSN  0003-6935. PMID  20134959.

(11) К. Ока, В. Отани, К. Камеяма, М. Кидай и Т. Такаги, Appl. Теор. Электрофор. 1: 273-278 (1990).

(12) К. Ока, В. Отани, Ю. Кубо, Ю. Засу и М. Акаги, заявка на патент США. 465, 186: Япония. Патент H7-5227 (1995 г.).

(16) С. Мори и Х. Окамото, Flotation 28: 1 (1980). (на японском языке): Fusen 28(3): 117 (1980).

(17) М. Смолуховский, в Handbuch der Electrizitat und des Magnetismus. (Л. Грейц. Ред.). Барт, Лерипциг, 1921, стр. 379.

(18) П. Уайт, Phil. Mag. S 7, 23, № 155 (1937).

(19) С. Комагат, Res. Electrotech. Lab. (Япония) 348, март 1933 г.

(20) Y. Fukui, S. Yuu и K. Ushiki, Power Technol. 54: 165 (1988).