Сигмовидная функция
Математическая функция, имеющая характерную S-образную кривую или сигмовидную кривую.

Логистическая кривая
График функции ошибки

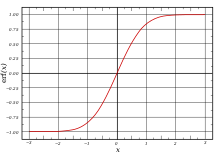
Сигмовидная функция — это любая математическая функция , график которой имеет характерную S-образную или сигмоидальную кривую .

Распространенным примером сигмоидальной функции является логистическая функция , которая определяется формулой: [1]

σ ( х ) = 1 1 + е − х = е х 1 + е х = 1 − σ ( − х ) . {\displaystyle \сигма (x)={\frac {1}{1+e^{-x}}}={\frac {e^{x}}{1+e^{x}}}=1-\сигма (-x).}

Другие сигмоидальные функции приведены в разделе Примеры. В некоторых областях, особенно в контексте искусственных нейронных сетей , термин «сигмоидальная функция» используется как синоним «логистической функции».

Частные случаи сигмоидальной функции включают кривую Гомпертца (используется в системах моделирования, которые насыщаются при больших значениях x) и кривую Ogee (используется в водосбросах некоторых плотин ). Сигмоидальные функции имеют область определения всех действительных чисел , при этом возвращаемое значение (отклик) обычно монотонно увеличивается, но может и уменьшаться. Сигмоидальные функции чаще всего показывают возвращаемое значение (ось y) в диапазоне от 0 до 1. Другой часто используемый диапазон — от −1 до 1.

В качестве функции активации искусственных нейронов использовались самые разные сигмоидальные функции, включая логистическую и гиперболическую тангенсную . Сигмоидальные кривые также распространены в статистике как кумулятивные функции распределения (которые идут от 0 до 1), такие как интегралы логистической плотности , нормальной плотности и функции плотности вероятности Стьюдента t . Логистическая сигмоидальная функция обратима, и ее обратная функция — логит- функция.

Определение

Сигмоидальная функция — это ограниченная , дифференцируемая , действительная функция, которая определена для всех действительных входных значений и имеет неотрицательную производную в каждой точке [1] [2] и ровно одну точку перегиба .


Характеристики

В общем случае сигмоидальная функция монотонна и имеет первую производную , которая имеет форму колокола . Наоборот, интеграл любой непрерывной, неотрицательной, колоколообразной функции (с одним локальным максимумом и без локального минимума, если только она не вырождена ) будет сигмоидальным. Таким образом, кумулятивные функции распределения для многих распространенных распределений вероятностей являются сигмоидальными. Одним из таких примеров является функция ошибок , которая связана с кумулятивной функцией распределения нормального распределения ; другим является функция arctan , которая связана с кумулятивной функцией распределения распределения Коши .

Сигмоидальная функция ограничена парой горизонтальных асимптот : . х → ± ∞ {\displaystyle x\rightarrow \pm \infty }

Сигмоидальная функция является выпуклой для значений, меньших определенной точки, и вогнутой для значений, больших этой точки: во многих приведенных здесь примерах эта точка равна 0.

Примеры

Сравнение некоторых сигмоидных функций. На рисунке все функции нормализованы таким образом, что их наклон в начале координат равен 1.
  • Логистическая функция ф ( х ) = 1 1 + е − х {\displaystyle f(x)={\frac {1}{1+e^{-x}}}}
  • Гиперболический тангенс (смещенная и масштабированная версия логистической функции, представленной выше) ф ( х ) = танг ⁡ х = е х − е − х е х + е − х {\displaystyle f(x)=\tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}
  • Функция арктангенса ф ( х ) = арктан ⁡ х {\displaystyle f(x)=\arctan x}
  • Функция Гудермана ф ( х ) = боже мой ⁡ ( х ) = ∫ 0 х г т дубинка ⁡ т = 2 арктан ⁡ ( танг ⁡ ( х 2 ) ) {\displaystyle f(x)=\operatorname {gd} (x)=\int _{0}^{x}{\frac {dt}{\cosh t}}=2\arctan \left(\tanh \left({\frac {x}{2}}\right)\right)}
  • Функция ошибки ф ( х ) = ерф ⁡ ( х ) = 2 π ∫ 0 х е − т 2 г т {\displaystyle f(x)=\operatorname {erf} (x)={\frac {2}{\sqrt {\pi }}}\int _{0}^{x}e^{-t^{2}}\,dt}
  • Обобщенная логистическая функция ф ( х ) = ( 1 + е − х ) − α , α > 0 {\displaystyle f(x)=\left(1+e^{-x}\right)^{-\альфа},\quad \альфа >0}
  • Функция Smoothstep ф ( х ) = { ( ∫ 0 1 ( 1 − ты 2 ) Н г ты ) − 1 ∫ 0 х ( 1 − ты 2 ) Н   г ты , | х | ≤ 1 знак ⁡ ( х ) | х | ≥ 1 Н ∈ З ≥ 1 {\displaystyle f(x)={\begin{cases}{\displaystyle \left(\int _{0}^{1}\left(1-u^{2}\right)^{N}du\right)^{-1}\int _{0}^{x}\left(1-u^{2}\right)^{N}\ du},&|x|\leq 1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\quad N\in \mathbb {Z} \geq 1}
  • Некоторые алгебраические функции , например ф ( х ) = х 1 + х 2 {\displaystyle f(x)={\frac {x}{\sqrt {1+x^{2}}}}}
  • и в более общем виде [3] ф ( х ) = х ( 1 + | х | к ) 1 / к {\displaystyle f(x)={\frac {x}{\left(1+|x|^{k}\right)^{1/k}}}}
  • С точностью до сдвигов и масштабирования многие сигмоиды являются частными случаями, где — обратное отрицательному преобразованию Бокса–Кокса значение , а и — параметры формы. [4] ф ( х ) = φ ( φ ( х , β ) , α ) , {\displaystyle f(x)=\varphi (\varphi (x,\beta),\alpha),} φ ( х , λ ) = { ( 1 − λ х ) 1 / λ λ ≠ 0 е − х λ = 0 {\displaystyle \varphi (x,\lambda )={\begin{cases}(1-\lambda x)^{1/\lambda }&\lambda \neq 0\\e^{-x}&\lambda =0\\\end{cases}}} α < 1 {\displaystyle \альфа <1} β < 1 {\displaystyle \бета <1}
  • Функция плавного перехода [5], нормализованная к (-1,1):

ф ( х ) = { 2 1 + е − 2 м х 1 − х 2 − 1 , | х | < 1 знак ⁡ ( х ) | х | ≥ 1 = { танг ⁡ ( м х 1 − х 2 ) , | х | < 1 знак ⁡ ( х ) | х | ≥ 1 {\displaystyle {\begin{align}f(x)&={\begin{cases}{\displaystyle {\frac {2}{1+e^{-2m{\frac {x}{1-x^{2}}}}}}-1},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\\&={\begin{cases}{\displaystyle \tanh \left(m{\frac {x}{1-x^{2}}}\right)},&|x|<1\\\\\operatorname {sgn}(x)&|x|\geq 1\\\end{cases}}\end{align}}} с использованием гиперболического тангенса, упомянутого выше. Здесь, — свободный параметр, кодирующий наклон в точке , который должен быть больше или равен , поскольку любое меньшее значение приведет к функции с несколькими точками перегиба, которая, следовательно, не является истинной сигмоидой. Эта функция необычна, поскольку она фактически достигает предельных значений -1 и 1 в пределах конечного диапазона, что означает, что ее значение постоянно при -1 для всех и при 1 для всех . Тем не менее, она гладкая (бесконечно дифференцируемая, ) всюду , включая . м {\displaystyle м} х = 0 {\displaystyle x=0} 3 {\displaystyle {\sqrt {3}}} х ≤ − 1 {\displaystyle x\leq -1} х ≥ 1 {\displaystyle x\geq 1} С ∞ {\displaystyle C^{\infty}} х = ± 1 {\displaystyle x=\pm 1}

Приложения

Перевернутая логистическая S-образная кривая для моделирования связи между урожайностью пшеницы и засоленностью почвы

Многие естественные процессы, такие как кривые обучения сложных систем , демонстрируют прогрессию от небольших начал, которая ускоряется и приближается к кульминации с течением времени. Когда отсутствует конкретная математическая модель, часто используется сигмоидальная функция. [6]

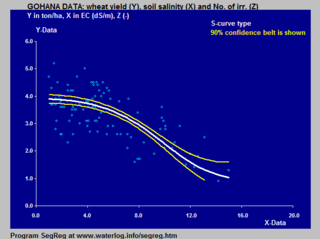
Модель Ван Генухтена–Гупты основана на перевернутой S-образной кривой и применяется к реакции урожайности сельскохозяйственных культур на засоление почвы .

Примеры применения логистической S-образной кривой к реакции урожайности сельскохозяйственных культур (пшеницы) на засоление почвы и глубину залегания грунтовых вод в почве показаны в разделе «Моделирование реакции сельскохозяйственных культур в сельском хозяйстве» .

В искусственных нейронных сетях иногда для повышения эффективности используются негладкие функции; они известны как жесткие сигмоиды .

В обработке аудиосигналов сигмоидальные функции используются в качестве передаточных функций формирователя волн для имитации звука ограничения аналоговых схем . [7]

В биохимии и фармакологии уравнения Хилла и Хилла–Ленгмюра являются сигмоидальными функциями.

В компьютерной графике и рендеринге в реальном времени некоторые сигмоидальные функции используются для плавного смешивания цветов или геометрии между двумя значениями, без видимых швов или разрывов.

Кривые титрования между сильными кислотами и сильными основаниями имеют сигмоидальную форму из-за логарифмического характера шкалы pH .

Логистическую функцию можно эффективно рассчитать, используя Unums типа III . [8]

Была построена иерархия сигмоидальных моделей роста с возрастающей сложностью (числом параметров) [9] с основной целью повторного анализа кинетических данных, так называемых кривых Nt, из экспериментов по гетерогенному зародышеобразованию [10] , в электрохимии . В настоящее время иерархия включает три модели с 1, 2 и 3 параметрами, если не считать максимального числа зародышей N max , соответственно — модель на основе tanh 2 под названием α 21 [11], первоначально разработанная для описания ограниченного диффузией роста кристаллов (не агрегации!) в 2D, модель Джонсона-Меля-Аврами-Колмогорова (JMAKn) [12] , и модель Ричардса [13] . Было показано, что для конкретной цели подходит даже самая простая модель, и, таким образом, подразумевалось, что рассмотренные эксперименты являются примером двухэтапного зародышеобразования, где первым этапом является рост метастабильной фазы, в которой образуются зародыши стабильной фазы [9] .

Смотрите также

На Викискладе есть медиафайлы по теме «Сигмовидные функции» .

Ссылки

  1. ^ ab Han, Jun; Morag, Claudio (1995). "Влияние параметров сигмоидальной функции на скорость обучения методом обратного распространения". В Mira, José; Sandoval, Francisco (ред.). От естественных к искусственным нейронным вычислениям . Lecture Notes in Computer Science. Vol. 930. pp. 195–201. doi :10.1007/3-540-59497-3_175. ISBN 978-3-540-59497-0.
  2. ^ Ling, Yibei; He, Bin (декабрь 1993 г.). «Энтропический анализ моделей биологического роста». IEEE Transactions on Biomedical Engineering . 40 (12): 1193– 2000. doi :10.1109/10.250574. PMID  8125495.
  3. ^ Даннинг, Эндрю Дж.; Кенслер, Дженнифер; Кудевиль, Лоран; Байе, Фабрис (28.12.2015). «Некоторые расширения в непрерывных методах для иммунологических коррелятов защиты». BMC Medical Research Methodology . 15 (107): 107. doi : 10.1186/s12874-015-0096-9 . PMC 4692073. PMID  26707389 . 
  4. ^ "grex --- Growth-curve Explorer". GitHub . 2022-07-09. Архивировано из оригинала 2022-08-25 . Получено 2022-08-25 .
  5. ^ EpsilonDelta (2022-08-16). «Функция плавного перехода в одном измерении | Серия «Функция плавного перехода», часть 1». 13:29/14:04 – через www.youtube.com.
  6. ^ Гиббс, Марк Н.; Маккей, Д. (ноябрь 2000 г.). «Вариационные гауссовские классификаторы процессов». Труды IEEE по нейронным сетям . 11 (6): 1458– 1464. doi :10.1109/72.883477. PMID  18249869. S2CID  14456885.
  7. ^ Смит, Джулиус О. (2010). Физическая обработка аудиосигнала (ред. 2010 г.). W3K Publishing. ISBN 978-0-9745607-2-4. Архивировано из оригинала 2022-07-14 . Получено 2020-03-28 .
  8. ^ Густафсон, Джон Л .; Йонемото, Айзек (12.06.2017). «Победа над числами с плавающей точкой в ​​их собственной игре: арифметика Posit» (PDF) . Архивировано (PDF) из оригинала 14.07.2022 . Получено 28.12.2019 .
  9. ^ ab Kleshtanova, Viktoria и Ivanov, Vassil V и Hodzhaoglu, Feyzim и Prieto, Jose Emilio и Tonchev, Vesselin (2023). "Гетерогенные подложки изменяют неклассические пути зародышеобразования: повторный анализ кинетических данных электроосаждения ртути на платине с использованием иерархии моделей сигмоидального роста". Кристаллы . 13 (12). MDPI: 1690. Bibcode : 2023Cryst..13.1690K. doi : 10.3390/cryst13121690 .{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  10. ^ Марков, И. и Стойчева, Е. (1976). «Плотность зародышей насыщения при электроосаждении металлов на инертных электродах II. Экспериментально». Тонкие твердые пленки . 35 (1). Elsevier: 21– 35. doi :10.1016/0040-6090(76)90109-7.{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
  11. ^ Иванов, В. В. и Тилеманн, К. и Аврамова, К. и Рейнш, С. и Тончев, В. (2023). «Моделирование кристаллизации: когда нормальная скорость роста зависит от пересыщения». Журнал физики и химии твердого тела . 181. Elsevier: 111542. doi : 10.1016/j.jpcs.2022.111542 (неактивен 2025-01-28).{{cite journal}}: CS1 maint: DOI inactive as of January 2025 (link) CS1 maint: multiple names: authors list (link)
  12. ^ Фанфони, М. и Томеллини, М. (1998). «Модель Джонсона-Мейла-Аврами-Кохногорова: краткий обзор». Il Nuovo Cimento D. 20. Springer : 1171– 1182. doi :10.1007/s002690050098.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  13. ^ Тьёрве, Э. и Тьёрве, К. М. Ц. (2010). «Унифицированный подход к семейству моделей Ричардса для использования в анализе роста: почему нам нужны только две формы моделей». Журнал теоретической биологии . 267 (3). Elsevier: 417– 425. doi :10.1016/j.jtbi.2010.02.027.{{cite journal}}: CS1 maint: multiple names: authors list (link)

Дальнейшее чтение

  • Митчелл, Том М. (1997). Машинное обучение . WCB McGraw–Hill . ISBN 978-0-07-042807-2.. (NB. В частности, см. «Главу 4: Искусственные нейронные сети» (в частности, стр. 96–97), где Митчелл использует слова «логистическая функция» и «сигмоидальная функция» как синонимы – эту функцию он также называет «сжимающей функцией» – а сигмоидальная (или логистическая) функция используется для сжатия выходных данных «нейронов» в многослойных нейронных сетях.)
  • Хамфрис, Марк. "Непрерывный вывод, сигмовидная функция". Архивировано из оригинала 2022-07-14 . Получено 2022-07-14 .(Примечание. Свойства сигмоиды, включая то, как она может смещаться вдоль осей и как может трансформироваться ее область определения.)
  • "Подгонка логистических S-кривых (сигмоидов) к данным с использованием SegRegA". Архивировано из оригинала 2022-07-14.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Sigmoid_function&oldid=1273059335"