Модифицированный гиперболический тангенс Соболевой
Математическая функция активации в анализе данных

Модифицированный гиперболический тангенс Соболевой , также известный как (параметрическая) функция активации модифицированного гиперболического тангенса Соболевой ([P]SMHTAF), [примечание 1] представляет собой специальную S-образную функцию , основанную на гиперболическом тангенсе , заданную формулой

УравнениеУправление левым хвостомУправление правым хвостом
что-то ⁡ х = е а х − е − б х е с х + е − г х . {\displaystyle \operatorname {smht} x={\frac {e^{ax}-e^{-bx}}{e^{cx}+e^{-dx}}}.}

История

Эта функция была первоначально предложена как «модифицированный гиперболический тангенс» [nb 1] украинским ученым Еленой В. Соболевой ( Елена В. Соболева ) в качестве функции полезности для многокритериальной оптимизации и моделирования выбора при принятии решений . [1] [ 2] [3]

Практическое использование

С тех пор эта функция была введена в теорию и практику нейронных сетей . [4]

Он также использовался в экономике для моделирования потребления и инвестиций, [5] для аппроксимации вольт-амперных характеристик полевых транзисторов и светодиодов , [6] для проектирования антенных фидеров , [7] [ prezident publisher ] и анализа температур и плотностей плазмы в области дивертора термоядерных реакторов . [8]

Чувствительность к параметрам

Производная функции определяется по формуле:

что-то ′ ⁡ ( х ) ≐ а е а х + б е − б х е с х + е − г х − что-то ⁡ ( х ) с е с х − г е − г х е с х + е − г х {\displaystyle \operatorname {smht} '(x)\doteq {\frac {ae^{ax}+be^{-bx}}{e^{cx}+e^{-dx}}}-\operatorname {smht} (x){\frac {ce^{cx}-de^{-dx}}{e^{cx}+e^{-dx}}}}

Следующие условия сохраняют функцию ограниченной по оси y : a ≤ c , b ≤ d .

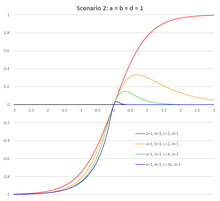
Было изучено семейство рекуррентно-генерируемых параметрических функций активации модифицированного гиперболического тангенса Соболевой (NPSMHTAF, FPSMHTAF) с параметрами a  = c и b  = d . [9] Стоит отметить, что в этом случае функция не чувствительна к перестановке параметров левой и правой сторон:

УравнениеРаспространенность левыхРаспространенность права
е а х − е − б х е а х + е − б х = е б х − е − а х е б х + е − а х {\displaystyle {\frac {e^{ax}-e^{-bx}}{e^{ax}+e^{-bx}}} = {\frac {e^{bx}-e^{-ax}}{e^{bx}+e^{-ax}}}}

Функция чувствительна к соотношению коэффициентов знаменателя и часто используется без коэффициентов в числителе:

УравнениеБазовая схемаМасштабируемая функция
тссс ⁡ х = е х − е − х е α х + е − β х . {\displaystyle \operatorname {ssht} x={\frac {e^{x}-e^{-x}}{e^{\alpha x}+e^{-\beta x}}}.}

Экстремальные оценки: х мин = 1 2 вн ⁡ β − 1 β + 1 ; {\displaystyle x_{\min }={\frac {1}{2}}\ln {\frac {\beta -1}{\beta +1}};} х макс = 1 2 вн ⁡ α + 1 α − 1 . {\displaystyle x_{\max }={\frac {1}{2}}\ln {\frac {\alpha +1}{\alpha -1}}.}

При параметрах a  = b  = c  = d  = 1 модифицированная функция гиперболического тангенса сводится к обычной функции tanh ( x ), тогда как при a  = b  = 1 и c  = d  = 0 этот член становится равным sinh ( x ).

Смотрите также

Примечания

  1. ^ ab Соболева предложила название «модифицированный гиперболический тангенс» (mtanh, mth), но поскольку другие авторы использовали это название также для других функций, некоторые авторы стали называть эту функцию «модифицированным гиперболическим тангенсом Соболевой».

Ссылки

  1. ^ Соболева, Елена Владимировна; Бескоровайный, Владимир Валентинович (2008). Функция полезности в задачах структурной оптимизации распределенных объектов Функция для оценки полезности альтернатива в задачах структурной оптимизации распределенных объектов. Четвертая научная конференция Харьковского университета имени Ивана Кожедуба, 16–17 квітня 2008 г. (Четвертая научная конференция Харьковского университета Воздушных Сил имени Ивана Кожедуба, 16–17 апреля 2008 г.) (на русском языке). Харьков, Украина: Харьковский университет воздушных сил (ХУПС/ХУПС). п. 121.
  2. ^ Соболева, Елена Владимировна (2009). S-образная функция полезности частных измерений для многофакторной оценки проектных решений[ S-образная функция полезности отдельных критериев для многокритериального принятия решений в дизайне ]. Материалы XIII Международного молодежного форума «Радиоэлектро-ника и молодежь в XXI веке» (Материалы 13-го международного молодежного форума «Радиоэлектроника и молодежь в XXI веке») (на русском языке). Харьков, Украина: Харьковский национальный университет радиоэлектроники (ХНУРЭ/ХНУРЕ). п. 247.
  3. ^ Бескоровайный, Владимир Валентинович; Соболева, Елена Владимировна (2010). ИДЕНТИФИКАЦИЯ ЧАСТНОЙ ПОЛЕЗНОСТИ МНОГОФАКТОРНЫХ АЛЬТЕРНАТИВ С ПОМОЩЬЮ С-ОБРАЗНЫХ ФУНКЦИЙ (PDF) . Проблемы бионики: Республиканский Межведомственный Научно-Технический Сборник БИОНИКА ИНТЕЛЛЕКТА[ Бионика интеллекта ] (на русском языке). Том 72, № 1. Харьковский национальный университет радиоэлектроники (ХНУРЭ/ХНУРЭ). С.  50–54 . ISSN  0555-2656. УДК 519.688: 004.896. Архивировано (PDF) из оригинала 21.06.2022 . Получено 19.06.2020 .(5 страниц) [1]
  4. ^ Малинова, Анна; Голев, Ангел; Илиев, Антон; Кюркчиев, Николай (август 2017 г.). "Семейство рекуррентных генерирующих активационных функций на основе функции Гудермана" (PDF) . Международный журнал инженерных исследований и исследований управления . 4 (8). Факультет математики и информатики, Университет Пловдива "Паисий Хилендарский", Пловдив, Болгария: 38– 48. ISSN  2394-7659. Архивировано (PDF) из оригинала 2022-07-14 . Получено 2020-06-19 .(11 страниц) [2]
  5. ^ Орландо, Джузеппе (2016-07-01). «Дискретная математическая модель для хаотической динамики в экономике: модель Калдора для бизнес-цикла». Математика и компьютеры в моделировании . 8-й семинар СТРУКТУРНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ: вычислительные аспекты; под редакцией Николетты Дель Буоно, Роберто Гарраппы и Джулии Спалетты и нестандартные приложения компьютерной алгебры (ACA'2013); под редакцией Франциско Ботана, Антонио Эрнандо, Эухенио Роанес-Лозано и Майкла Дж. Вестера. 125 : 83– 98. doi :10.1016/j.matcom.2016.01.001. ISSN  0378-4754.
  6. ^ Туев, Василий И.; Ужанин, Максим В. (2009). ПРИМЕНЕНИЕ МОДИФИЦИРОВАННОЙ ФУНКЦИИ ГИПЕРБОЛИЧЕСКОГО ТАНГЕНСА ДЛЯ АППРОКСИМАЦИИ ВОЛЬТАМПЕРНЫХ ХАРАКТЕРИСТИК ПОЛЕВЫХ ТРАНЗИСТОРОВ . Томск, Россия: Томский политехнический университет (ТПУ/ТПУ). С.  135–138 . № 4/314. Архивировано из оригинала 15 августа 2017 г. Проверено 5 ноября 2015 г.(4 страницы) [3]
  7. ^ Голев, Ангел; Джамийков, Тодор; Кюркчиев, Николай (2017-11-23) [2017-10-09, 2017-08-19]. "Сигмоидальные функции в антенно-фидерной технике" (PDF) . Международный журнал чистой и прикладной математики . 116 (4). Факультет математики и информатики, Университет Пловдива "Паисий Хилендарский", Пловдив, Болгария / Технический университет Софии , София, Болгария: Academic Publications, Ltd.: 1081– 1092. doi :10.12732/ijpam.v116i4.23 (неактивен 2024-11-01). ISSN  1311-8080. Архивировано (PDF) из оригинала 2020-06-19 . Получено 2020-06-19 .{{cite journal}}: CS1 maint: DOI неактивен по состоянию на ноябрь 2024 г. ( ссылка )(12 страниц)
  8. ^ Рубино, Джулио (15 января 2018 г.) [14 января 2018 г.]. Анализ данных о выхлопных газах и моделирование усовершенствованной конфигурации дивертора (Диссертация). Докторская степень по совместным исследованиям в области термоядерной науки и техники XXX (на английском, итальянском и португальском языках). Падуя, Италия: Centro Ricerche Fusione (CRF), Университет Падуи / Университет Неаполя Федерико II / Высший технический институт (IST), Университет Лиссабона . п. 84. ID 10811. Архивировано из оригинала 19 июня 2020 г. Проверено 19 июня 2020 г.{{cite book}}: CS1 maint: bot: original URL status unknown (link)(2+viii+3*iii+102 страницы)
  9. ^ Голев, Ангел; Илиев, Антон; Кюркчиев, Николай (июнь 2017 г.). "Заметка о функции активации модифицированного гиперболического тангенса Соболева" (PDF) . Международный журнал инновационной науки, техники и технологий (JISET) . 4 (6). Факультет математики и информатики, Университет Пловдива "Паисий Хилендарский", Пловдив, Болгария: 177– 182. ISSN  2348-7968. Архивировано (PDF) из оригинала 2020-06-19 . Получено 2020-06-19 .(6 страниц) [4]

Дальнейшее чтение

  • Илиев, Антон; Кюркчиев, Николай; Марков, Светослав (2017). "Заметка о новой функции активации типа Гомпертца". Biomath Communications . 4 (2). Факультет математики и информатики, Университет Пловдива "Паисий Хилендарский", Пловдив, Болгария / Институт математики и информатики, Болгарская академия наук , София, Болгария: Biomath Forum (BF). doi : 10.11145/10.11145/bmc.2017.10.201 . ISSN  2367-5233. Архивировано из оригинала 20.06.2020 . Получено 19.06.2020 .(20 страниц) [5]
Retrieved from "https://en.wikipedia.org/w/index.php?title=Soboleva_modified_hyperbolic_tangent&oldid=1254972439"