Тессеракты с руническими завитками

Тессеракт	Тессеракт Runcinated (16-ячеечный Runcinated)	16-ячеечный
Тессеракт Runcitucated (Runcicantellated 16-cell)	Тессеракт усеченный ранцитовый (Runcicantellated tesseract)	Усеченный тессеракт (Усеченный 16-ячейковый)
Ортогональные проекции в плоскости Коксетера B 4

В четырехмерной геометрии ранцинированный тессеракт ( или ранцинированный 16-ячейник ) — это выпуклый однородный 4-мерный многогранник , являющийся ранцинацией (усечением 3-го порядка) правильного тессеракта .

Существует 4 варианта выполнения тессеракта, включая перестановки, усечения и сокращения.

Тессеракт Runcinated
Диаграмма Шлегеля с 16 тетраэдрами
Тип	Однородный 4-многогранник
Символ Шлефли	т 0,3 {4,3,3}
Диаграммы Коксетера
Клетки	80	16 3.3.3 32 3.4.4 32 4.4.4
Лица	208	64 {3} 144 {4}
Края	192
Вершины	64
Вершинная фигура	Равносторонний треугольный антиподий
Группа симметрии	B 4 , [3,3,4], порядок 384
Характеристики	выпуклый
Единый индекс	14 15 16

Тессеракт с рутинными гранями или (малый) диспризматотессерактигексадекахорон имеет 16 тетраэдров , 32 куба и 32 треугольные призмы . Каждая вершина делится между 4 кубами, 3 треугольными призмами и одним тетраэдром.

Runcinated tesseract может быть построен путем расширения ячеек тессеракта радиально и заполнения пробелов тетраэдрами (вершинными фигурами), кубами (гранными призмами) и треугольными призмами (реберными призмами). Тот же процесс, примененный к 16-ячейке, также дает ту же самую фигуру.

Декартовы координаты вершин тессеракта с длиной ребра 2 являются перестановками:

${\displaystyle \left(\pm 1,\ \pm 1,\ \pm 1,\ \pm (1+{\sqrt {2}})\right)}$

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График
Диэдральная симметрия	[12/3]	[4]

Диаграммы Шлегеля

Каркас

Каркас из 16 тетраэдров .

Каркас с 32 треугольными призмами .

Восемь кубических ячеек соединены с другими 24 кубическими ячейками через все 6 квадратных граней. Другие 24 кубические ячейки соединены с первыми 8 ячейками только через две противоположные квадратные грани; оставшиеся 4 грани соединены с треугольными призмами. Треугольные призмы соединены с тетраэдрами через свои треугольные грани.

Тессеракт с рутинными гранями можно разбить на 2 кубических купола и ромбокубооктаэдрическую призму между ними. Это разбиение можно рассматривать как аналог разбиения трехмерного ромбокубооктаэдра на два квадратных купола и центральную восьмиугольную призму .

кубический купол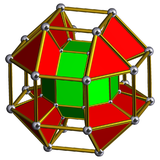

ромбокубооктаэдрическая призма

Ортографическая проекция куба-первого тессеракта runcinated в трехмерное пространство имеет (маленькую) ромбокубооктаэдрическую оболочку. Изображения ее ячеек располагаются внутри этой оболочки следующим образом:

• Ближайший и самый дальний куб от точки обзора 4d проецируется в кубический объем в центре оболочки.
• Шесть кубоидальных объемов соединяют этот центральный куб с 6 осевыми квадратными гранями ромбокубооктаэдра. Это изображения 12 кубических ячеек (каждая пара кубов разделяет изображение).
• 18 квадратных граней оболочки являются изображениями других кубических ячеек.
• 12 клиновидных объемов, соединяющих ребра центрального куба с неосевыми квадратными гранями оболочки, являются изображениями 24 треугольных призм (по паре ячеек на изображение).
• 8 треугольных граней оболочки являются изображениями оставшихся 8 треугольных призм.
• Наконец, 8 тетраэдрических объемов, соединяющих вершины центрального куба с треугольными гранями оболочки, являются изображениями 16 тетраэдров (опять же, по паре ячеек на изображение).

Эта схема ячеек в проекции аналогична схеме граней (маленького) ромбокубооктаэдра при проекции на 2 измерения. Ромбокубооктаэдр также построен из куба или октаэдра аналогичным образом, что и тессеракт runcinated. Следовательно, тессеракт runcinated можно рассматривать как 4-мерный аналог ромбокубооктаэдра.

Runcitucated тессеракт
Диаграмма Шлегеля, центрированная на усеченном кубе, с кубооктаэдрическими ячейками.
Тип	Однородный 4-многогранник
Символ Шлефли	т 0,1,3 {4,3,3}
Диаграммы Коксетера
Клетки	80	8 3.4.4 16 3.4.3.4 24 4.4.8 32 3.4.4
Лица	368	128 {3} 192 {4} 48 {8}
Края	480
Вершины	192
Вершинная фигура	Прямоугольная пирамида
Группа симметрии	B 4 , [3,3,4], порядок 384
Характеристики	выпуклый
Единый индекс	18 19 20

Тессеракт с усечённой вершиной , 16-ячейковый рунцикантеллированный или призматоромбатированный гексадекахорон ограничен 80 ячейками: 8 усечёнными кубами , 16 кубооктаэдрами , 24 восьмиугольными призмами и 32 треугольными призмами .

Тессеракт runciturcated может быть построен из усеченного тессеракта путем расширения ячеек усеченного куба наружу радиально и вставки восьмиугольных призм между ними. В процессе тетраэдры расширяются в кубооктаэдры, а треугольные призмы заполняют оставшиеся промежутки.

Декартовы координаты вершин усеченного тессеракта с длиной ребра 2 задаются всеми перестановками:

${\displaystyle \left(\pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+{\sqrt {2}}),\ \pm (1+2{\sqrt {2}})\right)}$

В первой параллельной проекции усеченного куба усеченного тессеракта в трехмерное пространство проекционное изображение выглядит следующим образом:

• Проекционная оболочка представляет собой неоднородный (маленький) ромбокубооктаэдр с 6 квадратными гранями и 12 прямоугольными гранями.
• Две ячейки усеченного куба проецируются на усеченный куб в центре проекционной оболочки.
• Шесть восьмиугольных призм соединяют этот центральный усеченный куб с квадратными гранями оболочки. Это изображения 12 ячеек восьмиугольной призмы, по две ячейки на каждое изображение.
• Оставшиеся 12 восьмиугольных призм проецируются на прямоугольные грани оболочки.
• Шесть квадратных граней оболочки являются изображениями оставшихся шести ячеек усеченного куба.
• Двенадцать прямоугольных треугольных призм соединяют внутренние восьмиугольные призмы. Это изображения 24 ячеек треугольной призмы. Остальные 8 треугольных призм проецируются на треугольные грани оболочки.
• Оставшиеся 8 объемов, лежащих между треугольными гранями оболочки и внутренним усеченным кубом, являются изображениями 16 кубооктаэдрических ячеек, по паре ячеек на каждое изображение.

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График
Диэдральная симметрия	[12/3]	[4]

Стереографическая проекция со 128 синими треугольными гранями и 192 зелеными четырехугольными гранями.

Runcitucated 16-ячеечный
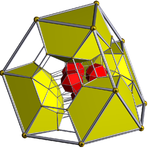Диаграммы Шлегеля, центрированные на ромбокубооктаэдре и усеченном тетраэдре
Тип	Однородный 4-многогранник
Символ Шлефли	т 0,1,3 {3,3,4}
Диаграмма Коксетера
Клетки	80	8 3.4.4.4 16 3.6.6 24 4.4.4 32 4.4.6
Лица	368	64 {3} 240 {4} 64 {6}
Края	480
Вершины	192
Вершинная фигура	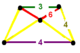Трапециевидная пирамида
Группа симметрии	B 4 , [3,3,4], порядок 384
Характеристики	выпуклый
Единый индекс	19 20 21

Ранцикантеллированный 16-ячеечный тессеракт , ранцикантеллированный тессеракт или призматоромбатированный тессеракт ограничен 80 ячейками : 8 ромбокубооктаэдрами , 16 усеченными тетраэдрами , 24 кубами и 32 шестиугольными призмами .

Runciturcated 16-ячейка может быть построена путем сжатия малых ромбокубооктаэдрических ячеек кантеллированного тессеракта радиально и заполнения пространства между ними кубами. В процессе октаэдрические ячейки расширяются в усеченные тетраэдры (половина их треугольных граней расширяется в шестиугольники путем растягивания ребер), а треугольные призмы расширяются в шестиугольные призмы (каждая со своими тремя исходными квадратными гранями, соединенными, как и прежде, с малыми ромбокубооктаэдрами, и своими тремя новыми квадратными гранями, соединенными с кубами).

Вершины усеченного 16-клеточного графа с длиной ребра 2 задаются всеми перестановками следующих декартовых координат :

${\displaystyle \left(\pm 1,\ \pm 1,\ \pm (1+{\sqrt {2}}),\ \pm (1+2{\sqrt {2}})\right)}$

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График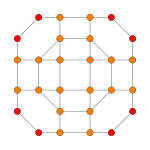
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График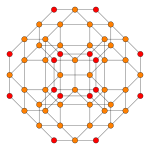
Диэдральная симметрия	[12/3]	[4]

Малые ромбокубооктаэдрические ячейки соединены своими 6 осевыми квадратными гранями с кубическими ячейками и соединены своими 12 неосевыми квадратными гранями с шестиугольными призмами. Кубические ячейки соединены с ромбокубооктаэдрами через 2 противоположные грани и соединены с шестиугольными призмами через оставшиеся 4 грани. Шестиугольные призмы соединены с усеченными тетраэдрами через их шестиугольные грани, а с ромбокубооктаэдрами через 3 их квадратных грани каждая, и с кубами через другие 3 квадратных грани. Усеченные тетраэдры соединены с ромбокубооктаэдрами через их треугольные грани, а с шестиугольными призмами через их шестиугольные грани.

Ниже приведена схема ячеек усеченного 16-ячеечного многогранника в параллельной проекции, сначала малого ромбокубооктаэдра, в трехмерное пространство:

• Проекционная оболочка представляет собой усеченный кубооктаэдр .
• Шесть малых ромбокубооктаэдров проецируются на 6 восьмиугольных граней этой оболочки, а два других проецируются на малый ромбокубооктаэдр, лежащий в центре этой оболочки.
• Шесть кубоидальных объемов, соединяющих осевые квадратные грани центрального малого ромбокубооктаэдра с центром восьмиугольников, соответствуют изображению 12 кубических ячеек (каждая пара из двенадцати имеет одно и то же изображение).
• Оставшиеся 12 кубических ячеек проецируются на 12 квадратных граней большой ромбокубооктаэдрической оболочки.
• 8 объемов, соединяющих шестиугольники оболочки с треугольными гранями центрального ромбокубооктаэдра, являются изображениями 16 усеченных тетраэдров.
• Оставшиеся 12 пространств, соединяющих неосевые квадратные грани центрального малого ромбокубооктаэдра с квадратными гранями оболочки, являются изображениями 24 шестиугольных призм.
• Наконец, последние 8 шестиугольных призм проецируются на шестиугольные грани оболочки.

Такое расположение ячеек похоже на расположение граней большого ромбокубооктаэдра при проекции в 2-мерное пространство. Следовательно, усеченный 16-ячейник можно рассматривать как один из 4-мерных аналогов большого ромбокубооктаэдра. Другим аналогом является усеченный тессеракт .

Всеусеченный тессеракт
Диаграмма Шлегеля , в центре которой усеченный кубооктаэдр, показаны усеченные октаэдрические ячейки.
Тип	Однородный 4-многогранник
Символ Шлефли	т 0,1,2,3 {3,3,4}
Диаграмма Коксетера
Клетки	80	8 4.6.8 16 4.6.6 24 4.4.8 32 4.4.6
Лица	464	288 {4} 128 {6} 48 {8}
Края	768
Вершины	384
Вершинная фигура	Хиральный разносторонний тетраэдр
Группа симметрии	B 4 , [3,3,4], порядок 384
Характеристики	выпуклый
Единый индекс	20 21 22

Всеусеченный тессеракт , всеусеченный 16-ячейниковый или большой диспризматотессерактигексадекахорон ограничен 80 ячейками : 8 усеченными кубооктаэдрами , 16 усеченными октаэдрами , 24 восьмиугольными призмами и 32 шестиугольными призмами .

Омнитусечённый тессеракт может быть построен из кантитусечённого тессеракта путём радиального смещения усечённых кубооктаэдрических ячеек так, чтобы между их восьмиугольными гранями можно было вставить восьмиугольные призмы. В результате треугольные призмы расширяются в шестиугольные призмы, а усечённые тетраэдры расширяются в усечённые октаэдры.

Декартовы координаты вершин всеусеченного тессеракта с длиной ребра 2 задаются всеми перестановками координат и знаками:

${\displaystyle \left(1,\ 1+{\sqrt {2}},\ 1+2{\sqrt {2}},\ 1+3{\sqrt {2}}\right)}$

Ячейки усеченных кубооктаэдров соединены с восьмиугольными призмами через их восьмиугольные грани, усеченные октаэдры через их шестиугольные грани, а шестиугольные призмы через их квадратные грани. Восьмиугольные призмы соединены с шестиугольными призмами и усеченными октаэдрами через их квадратные грани, а шестиугольные призмы соединены с усеченными октаэдрами через их шестиугольные грани.

В матрице конфигурации показаны все подсчеты инцидентности между элементами. Диагональные числа f-вектора выводятся с помощью построения Витхоффа , разделяющего полный групповой порядок подгруппового порядка путем удаления одного зеркала за раз. Края существуют в 4 позициях симметрии. Квадраты существуют в 3 позициях, шестиугольники в 2 позициях и восьмиугольники в одной. Наконец, существуют 4 типа ячеек, центрированных на 4 углах фундаментального симплекса. ^[1]

Б 4		к -лицо	ф к	ф 0	ф 1				ф 2						ф 3				к -цифра	Примечания
		( )	ф 0	384	1	1	1	1	1	1	1	1	1	1	1	1	1	1	4.( )	В 4 = 384
А 1		{ }	ф 1	2	192	*	*	*	1	1	1	0	0	0	1	1	1	0	3.( )	В4 / А1 = 192
А 1		{ }		2	*	192	*	*	1	0	0	1	1	0	1	1	0	1		В4 / А1 = 192
А 1		{ }		2	*	*	192	*	0	1	0	1	0	1	1	0	1	1		В4 / А1 = 192
А 1		{ }		2	*	*	*	192	0	0	1	0	1	1	0	1	1	1		В4 / А1 = 192
А 2		{6}	ф 2	6	3	3	0	0	64	*	*	*	*	*	1	1	0	0	{ }	В4 / А2 = 64
А 1 А 1		{4}		4	2	0	2	0	*	96	*	*	*	*	1	0	1	0		Б 4 /А 1 А 1 = 96
А 1 А 1		{4}		4	2	0	0	2	*	*	96	*	*	*	0	1	1	0		Б 4 /А 1 А 1 = 96
А 2		{6}		6	0	3	3	0	*	*	*	64	*	*	1	0	0	1		В4 / А2 = 64
А 1 А 1		{4}		4	0	2	0	2	*	*	*	*	96	*	0	1	0	1		Б 4 /А 1 А 1 = 96
Б 2		{8}		8	0	0	4	4	*	*	*	*	*	48	0	0	1	1		В4 / В2 = 48
А 3		тр{3,3}	ф 3	24	12	12	12	0	4	6	0	4	0	0	16	*	*	*	( )	В4 / А3 = 16
А 2 А 1		{6}×{ }		12	6	6	0	6	2	0	3	0	3	0	*	32	*	*		В 4 /А 2 А 1 = 32
Б 2 А 1		{8}×{ }		16	8	0	8	8	0	4	4	0	0	2	*	*	24	*		В 4 /В 2 А 1 = 24
Б 3		тр{4,3}		48	0	24	24	24	0	0	0	8	12	6	*	*	*	8		В4 / В3 = 8

В первой параллельной проекции усеченного кубооктаэдра всеусеченного тессеракта в трех измерениях изображения его ячеек располагаются следующим образом:

• Проекционная оболочка имеет форму неоднородного усеченного кубооктаэдра.
• Два усеченных кубооктаэдра проецируются в центр проекционной оболочки.
• Оставшиеся 6 усеченных кубооктаэдров проецируются на (неправильные) восьмиугольные грани оболочки. Они соединены с центральным усеченным кубооктаэдром через 6 восьмиугольных призм, которые являются изображениями ячеек восьмиугольной призмы, по паре на каждое изображение.
• Восемь шестиугольных граней оболочки являются изображениями восьми шестиугольных призм.
• Оставшиеся шестиугольные призмы проецируются на 12 изображений нерегулярных шестиугольных призм, лежащих там, где были бы ребра куба. Каждое изображение соответствует двум ячейкам.
• Наконец, 8 объемов между шестиугольными гранями проекционной оболочки и шестиугольными гранями центрального усеченного кубооктаэдра являются изображениями 16 усеченных октаэдров, по две ячейки на каждое изображение.

Эта схема ячеек в проекции похожа на схему усеченного 16-ячеечного ранцитаэдра , которая аналогична схеме граней в проекции октаэдра-первого октагона усеченного кубооктаэдра в 2 измерениях. Таким образом, усеченный тессеракт можно рассматривать как еще один аналог усеченного кубооктаэдра в 4 измерениях.

ортографические проекции

самолет Коксетера	Б 4	Б 3 / Д 4 / А 2	Б 2 / Д 3
График
Диэдральная симметрия	[8]	[6]	[4]
самолет Коксетера	Ф 4	А 3
График
Диэдральная симметрия	[12/3]	[4]

Перспективные проекции
Перспективная проекция, центрированная на одной из усеченных кубооктаэдрических ячеек, выделенных желтым цветом. Шесть окружающих восьмиугольных призм показаны синим цветом, а оставшиеся ячейки — зеленым. Ячейки, скрытые с точки зрения 4D, отброшены для ясности.	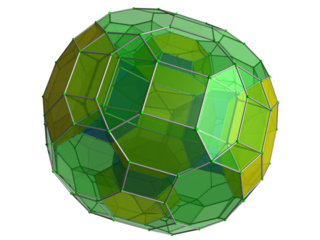Перспективная проекция, центрированная на одной из усеченных октаэдрических ячеек, выделенных желтым цветом. Четыре из окружающих шестиугольных призм показаны синим цветом, а еще 4 усеченных октаэдра на другой стороне этих призм также показаны желтым цветом. Ячейки, скрытые с точки зрения 4D, отброшены для ясности. Некоторые из других шестиугольных и восьмиугольных призм также можно различить на этом виде.
Стереографические проекции
В центре усеченный кубооктаэдр	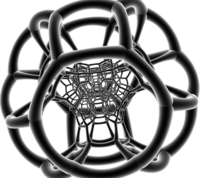В центре усеченный октаэдр

Сеть

Всеусеченный тессеракт

Двойственный к усеченному тессеракту

Полный плосконосый тессеракт или омнисконосый тессеракт , определяемый как чередование всеусеченного тессеракта, нельзя сделать однородным, но ему можно придать диаграмму Коксетера, и симметрия [4,3,3] ⁺ , и построен из 8 плосконосых кубов , 16 икосаэдров , 24 квадратных антипризм , 32 октаэдров (как треугольные антипризмы) и 192 тетраэдров , заполняющих пробелы в удаленных вершинах. Он имеет 272 ячейки, 944 грани, 864 ребра и 192 вершины. ^[2]

Биальтернатосноб 16-ячеечный или рунциковый снопистый выпрямленный 16-ячеечный , построенный путем удаления чередующихся длинных прямоугольников из восьмиугольников, также не является однородным. Как и омнисноб тессеракт, он имеет самую высокую конструкцию симметрии порядка 192 с 8 ромбокубооктаэдрами (с симметрией T _h ), 16 икосаэдрами (с симметрией T ), 24 прямоугольными трапециями (топологически эквивалентными кубу , но с симметрией D _2d ), 32 треугольными призмами , с 96 треугольными призмами (как клинья с симметрией C _s ), заполняющими промежутки. ^[3]

Вариант с правильными икосаэдрами и однородными треугольными призмами имеет две длины ребер в соотношении 1 : 2 и встречается как вершинная огранка чешуевидного рунического курносого 24-ячейника .

Многогранники симметрии B4
Имя	тессеракт	выпрямленный тессеракт	усеченный тессеракт	тессеракт с кантеллированными углами	рунический тессеракт	битусеченный тессеракт	усеченный тессеракт	бежатьусеченныйтессеракт ​	омниусеченный тессеракт
Диаграмма Коксетера		=				=
Символ Шлефли	{4,3,3}	т 1 {4,3,3} р{4,3,3}	т 0,1 {4,3,3} т{4,3,3}	т 0,2 {4,3,3} рр{4,3,3}	т 0,3 {4,3,3}	т 1,2 {4,3,3} 2т{4,3,3}	т 0,1,2 {4,3,3} тр{4,3,3}	т 0,1,3 {4,3,3}	т 0,1,2,3 {4,3,3}
Диаграмма Шлегеля
Б 4
Имя	16-ячеечный	выпрямленный 16-элементный	усеченный 16-клеточный	кантеллированный 16-ячеечный	16 -клеточный	усеченный 16-ячеечный	кантит-усеченный 16-клеточный	runcitucated 16-ячеечный	усеченный 16-ячеечный
Диаграмма Коксетера	=	=	=	=		=	=
Символ Шлефли	{3,3,4}	т 1 {3,3,4} р{3,3,4}	т 0,1 {3,3,4} т{3,3,4}	т 0,2 {3,3,4} рр{3,3,4}	т 0,3 {3,3,4}	т 1,2 {3,3,4} 2т{3,3,4}	т 0,1,2 {3,3,4} тр{3,3,4}	т 0,1,3 {3,3,4}	т 0,1,2,3 {3,3,4}
Диаграмма Шлегеля
Б 4

• Т. Госсет : О правильных и полуправильных фигурах в пространстве n измерений , Вестник математики, Макмиллан, 1900
• HSM Коксетер :
  • Коксетер, Правильные многогранники , (3-е издание, 1973), издание Дувра, ISBN 0-486-61480-8 , стр. 296, Таблица I (iii): Правильные многогранники, три правильных многогранника в n-мерности (n≥5) 
  • HSM Coxeter, Regular Polytopes , 3-е издание, Dover New York, 1973, стр. 296, Таблица I (iii): Regular Polytopes, три regular polytopes в n-мерностях (n≥5)
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] 
    • (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
    • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 409: Гемикубы: 1 _n1 ) 
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
• 2. Выпуклая однородная полихора на основе тессеракта (8-ячейковая) и гексадекахорона (16-ячейковая) - модели 15, 19, 20 и 21, Георгий Ольшевский.
• http://www.polytope.de/nr17.html
• Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».х3о3о4х - сидпит, х3о3х4х - прох, х3х3о4х - прит, х3х3х4х - гидпит

• H4 однородные многогранники с координатами: t03{4,3,3} t013{3,3,4} t013{4,3,3} t0123{4,3,3}