Подсчет стержней
| Часть серии статей о |
| Системы счисления |
|---|
| List of numeral systems |

| Подсчет стержней | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| китайское имя | |||||||||
| Традиционный китайский | 算籌 | ||||||||
| Упрощенный китайский | 算筹 | ||||||||
| |||||||||
| Альтернативное китайское название | |||||||||
| китайский | 算子 | ||||||||
| |||||||||
| вьетнамское имя | |||||||||
| вьетнамский алфавит | que tính / тоан тру | ||||||||
| Хан-Ном | 𣠗併 / 算籌 | ||||||||
| корейское имя | |||||||||
| Хангыль | 산가지 / 산목 | ||||||||
| Ханджа | Переводчик Google / Google | ||||||||
| |||||||||
| японское имя | |||||||||
| Кандзи | Переводчик Google | ||||||||
| Хирагана | さんぎ / さんちゅう | ||||||||
| |||||||||
Счетные палочки (筭) — это небольшие бруски, обычно длиной 3–14 см (от 1 до 6 дюймов), которые использовались математиками для вычислений в древней Восточной Азии . Они размещаются горизонтально или вертикально для представления любого целого или рационального числа .
Основанные на них письменные формы называются стержневыми цифрами . Они представляют собой настоящую позиционную систему счисления с цифрами для 1–9 и пробелом для 0, начиная с периода Воюющих царств (около 475 г. до н. э.) [1] и до XVI века.
История
Китайские арифметики использовали счетные палочки более двух тысяч лет назад.
В 1954 году в могиле № 15 Чу Цзуцзягуншань (左家公山) в Чанше , провинция Хунань , было найдено более сорока счетных стержней периода Воюющих царств (V в. до н. э. — 221 г. до н. э.). [2] [3] [ проверка не удалась ]
В 1973 году археологи обнаружили несколько деревянных письмен из гробницы в Хубэе, датируемых периодом династии Хань (206 г. до н. э. — 220 г. н. э.). На одном из деревянных письмен было написано: «当利二月定算𝍥». [ необходима цитата ] Это один из самых ранних примеров использования счетных палочек в письме.
Квадратная лакированная шкатулка, датируемая примерно 168 г. до н. э., содержащая квадратную шахматную доску с узорами TLV, шахматные фигуры, счетные палочки и другие предметы, была найдена в 1972 г. при раскопках Мавандуй M3, Чанша, провинция Хунань. [4] [5]
В 1976 году в уезде Цяньян в Шэньси была обнаружена связка счетных палочек из костей эпохи Западной Хань (202 г. до н. э. — 9 г. н. э.) . [6] [7] Использование счетных палочек должно было предшествовать этому; Суньцзы ( ок. 544 — ок. 496 г. до н. э.), военный стратег конца периода Весны и Осени с 771 г. до н. э. по 5 в. до н. э., упоминает об их использовании для выполнения расчетов, чтобы выиграть войну перед тем, как идти в бой; [8] Лао-цзы (умер в 531 г. до н. э.), писавший в период Воюющих царств, сказал: «хороший калькулятор не использует счетные палочки». [9] В « Книге Хань» (законченной в 111 г. н. э.) записано: «они считают с помощью бамбука, диаметром один фен, длиной шесть цуней, собранного в шестиугольную связку из двухсот семидесяти одной части». [10]
Сначала счетные стержни имели круглое сечение, но ко времени правления династии Суй (581–618 гг. н. э.) математики стали использовать треугольные стержни для представления положительных чисел и прямоугольные стержни для представления отрицательных чисел . [ необходима ссылка ]

После расцвета счетов [ когда? ] счетные палочки были заброшены, за исключением Японии, где палочные цифры превратились в символическую запись для алгебры .
Использование счетных палочек




Счетные стержни представляют цифры по количеству стержней, а перпендикулярный стержень представляет пять. Чтобы избежать путаницы, вертикальные и горизонтальные формы используются попеременно. Обычно вертикальные стержневые числа используются для положения единиц, сотен, десятков тысяч и т. д., в то время как горизонтальные стержневые числа используются для десятков, тысяч, сотен тысяч и т. д. В «Суньцзы суаньцзин» написано, что «один — вертикальный, десять — горизонтальный». [11]
Красные стержни представляют положительные числа , а черные стержни представляют отрицательные числа . [12] Древние китайцы ясно понимали отрицательные числа и ноль (оставляя для него пустое место), хотя у них не было символа для последнего. «Девять глав о математическом искусстве» , которые были в основном составлены в первом веке н. э., гласили: «(при использовании вычитания) вычитайте числа с одинаковыми знаками, сложите числа с разными знаками, вычтите положительное число из нуля, чтобы получить отрицательное число, и вычтите отрицательное число из нуля, чтобы получить положительное число». [13] [14] Позже для обозначения нуля иногда использовался камень го .
Это чередование вертикальной и горизонтальной формы стержневой цифры очень важно для правильного понимания письменной транскрипции стержневых цифр в рукописях. Например, в Licheng suanjin 81 было транскрибировано как , а 108 было транскрибировано как ; ясно, что последнее явно имело пустой ноль на «счетной доске» (т. е. полу или коврике), хотя в письменной транскрипции пробела не было. В той же рукописи 405 было транскрибировано как , с пустым пространством между ними по очевидным причинам, и никоим образом не могло быть интерпретировано как «45» . Другими словами, транскрибированные стержневые цифры могут не быть позиционными, но на счетной доске они позиционны. является точным изображением счетного стержневого числа 405 на столе или полу.









Место значения
Значение числа зависит от его физического положения на счетной доске. 9 в крайней правой позиции на доске означает 9. Перемещение партии стержней, представляющих 9, на одну позицию влево (т. е. на позицию десятков) дает 9[] или 90. Сдвиг влево на третью позицию (на позицию сотен) дает 9[][] или 900. Каждый раз, когда мы сдвигаем число на одну позицию влево, оно умножается на 10. Каждый раз, когда мы сдвигаем число на одну позицию вправо, оно делится на 10. Это применимо к однозначным или многозначным числам.
Математик династии Сун Цзя Сянь использовал рукописные китайские десятичные порядки 步十百千萬 в качестве разрядного значения стержневого числа, о чем свидетельствует факсимиле со страницы энциклопедии Юнлэ . Он аранжировал 七萬一千八百二十四 как
- Не забудьте про это
- Переводчик Google
Он рассматривал китайские порядковые номера как маркеры разрядных значений, и 七一八二四 стал разрядным десятичным числом. Затем он записал стержневые цифры в соответствии с их разрядным значением:
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 萬 | 千 | 百 | 十 | 步 |
 |  |  |  |  |
В Японии математики помещали счетные палочки на счетную доску, лист ткани с сетками, и использовали только вертикальные формы, опираясь на сетки. В японской книге по математике XVIII века есть диаграмма счетной доски с шашечками, с символами порядка величины "千百十一分厘毛" (тысяча, сто, десять, единица, десятая, сотая, тысячная). [15]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный |  |  |  |  |  |  |  |  |  | |
| Горизонтальный |  |  |  |  |  |  |  |  |  |
| 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | −9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный |  |  |  |  |  |  |  |  |  | |
| Горизонтальный |  |  |  |  |  |  | 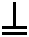 |  | 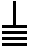 |
Примеры:
| 231 |  |  |  | |
|---|---|---|---|---|
| 5089 |  |  |  | |
| −407 |  |  | ||
| −6720 |  |  |  |
Стержневые цифры
Стержневые цифры — это позиционная система счисления, созданная из форм счетных стержней. Положительные числа пишутся так, как они есть, а отрицательные числа пишутся с наклонной чертой у последней цифры. Вертикальная черта в горизонтальных формах 6–9 рисуется короче, чтобы иметь одинаковую высоту символов.
Круг (〇) используется для обозначения 0. Многие историки считают, что он был заимствован из индийских цифр Гаутамой Сиддхой в 718 году [13] , но некоторые считают, что он был создан на основе китайского символа заполнения пробелов в тексте «□», а другие полагают, что индийцы заимствовали его из Китая, поскольку он напоминает конфуцианский философский символ, означающий «ничего». [16]
В XIII веке математики Южной Сун изменили цифры для 4, 5 и 9, чтобы сократить количество штрихов. [16] Новые горизонтальные формы в конечном итоге трансформировались в цифры Сучжоу . Японцы продолжали использовать традиционные формы.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный |  |  |  |  |  |  |  |  |  |  |
| Горизонтальный |  |  |  |  |  |  |  | 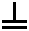 |  |  |
| 0 | −1 | −2 | −3 | −4 | −5 | −6 | −7 | −8 | −9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный |  |  |  | 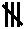 |  | 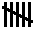 |  |  |  | 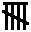 |
| Горизонтальный |  |  |  |  |  |  |  |  |  |  |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Вертикальный |  |  |  |  | 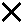 | 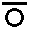 |  |  |  | 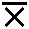 |
| Горизонтальный |  |  |  |  | 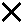 |  |  | 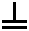 |  |  |
Примеры:
| Традиционный | Южная песня | |
|---|---|---|
| 231 |    |    |
| 5089 |     |     |
| −407 |    | 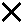   |
| −6720 |     |     |
В Японии Сэки Такакадзу развил стержневые цифры в символическую запись для алгебры и радикально улучшил японскую математику . [13] После его периода была разработана позиционная система счисления с использованием китайских цифровых иероглифов , а стержневые цифры использовались только для знаков плюс и минус .
| Западный | Секи | После Секи |
|---|---|---|
| х + у + 246 |   甲乙 甲乙   |   甲乙 甲乙 二四六 二四六 |
| 5 х − 6 лет |   甲乙 甲乙 |  五甲 五甲 六乙 六乙 |
| 7 ху |  甲乙 甲乙 |  Продолжить чтение Продолжить чтение |
| 8 х / у | Н/Д | 乙 八甲[ сомнительно – обсудить ] 八甲[ сомнительно – обсудить ] |
Дроби

Дробь выражалась с помощью стержневых цифр в виде двух стержневых цифр, расположенных одна над другой (без какого-либо другого символа, например, современной горизонтальной черты). [ необходима ссылка ]
Стержневое исчисление
Метод использования счетных стержней для математических вычислений назывался стержневым вычислением или стержневым исчислением (筹算). Стержневое исчисление может использоваться для широкого спектра вычислений, включая нахождение значения π , нахождение квадратных корней , кубических корней или корней более высокого порядка , а также решение систем линейных уравнений .
До введения письменного нуля пробел использовался для указания отсутствия единиц, а поворот символа в последующем столбце единиц на 90° был принят, чтобы помочь уменьшить неоднозначность в значениях записи, рассчитанных на стержнях. [17] Например, 107 (𝍠 𝍧) и 17 (𝍩𝍧) будут различаться поворотом, хотя несколько нулевых единиц могли привести к неоднозначности, например, 1007 (𝍩 𝍧) и 10007 (𝍠 𝍧). После того, как письменный ноль вошел в игру, стержневые цифры стали независимыми, и их использование действительно пережило счетные стержни после его замены на абак . Одна из разновидностей горизонтальных стержневых цифр, сучжоуские цифры, все еще используются для ведения бухгалтерского учета и в рецептах на травяную медицину в китайских кварталах в некоторых частях мира.
Юникод
Unicode 5.0 включает счетные стержневые цифры в их собственном блоке в Дополнительной многоязычной плоскости (SMP) от U+1D360 до U+1D37F. Кодовые точки для горизонтальных цифр 1–9 — от U+1D360 до U+1D368, а для вертикальных цифр 1–9 — от U+1D369 до U+1D371. Первые называются цифрами единиц , а вторые — цифрами десятков , [18] [19] что противоположно описанному выше соглашению. Стандарт Unicode гласит, что ориентация символов Unicode следует соглашению династии Сун, которое отличается от практики династии Хань, которая представляла цифры в виде вертикальных линий, а десятки — в виде горизонтальных линий. [20] Ноль должен быть представлен как U+3007 (〇, идеографическое число ноль), а отрицательный знак должен быть представлен как U+20E5 (объединяя наложение обратной косой черты). [21] Поскольку они были недавно добавлены в набор символов и включены в SMP, поддержка шрифтов все еще может быть ограничена.
| Счетные стержневые цифры [1] [2] Официальная таблица кодов Консорциума Unicode (PDF) | ||||||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | А | Б | С | Д | Э | Ф | |
| У+1Д36х | 𝍠 | 𝍡 | 𝍢 | 𝍣 | 𝍤 | 𝍥 | 𝍦 | 𝍧 | 𝍨 | 𝍩 | 𝍪 | 𝍫 | 𝍬 | 𝍭 | 𝍮 | 𝍯 |
| У+1Д37х | 𝍰 | 𝍱 | 𝍲 | 𝍳 | 𝍴 | 𝍵 | 𝍶 | 𝍷 | 𝍸 | |||||||
Примечания
| ||||||||||||||||
Смотрите также
Ссылки
- ^ Лэй-Йонг, Лам (1986). «Концептуальные истоки нашей системы счисления и символическая форма алгебры». Архив истории точных наук . 36 (3): 183– 195. ISSN 0003-9519.
- ^ 中国独特的计算工具, заархивировано из оригинала 21 ноября 2007 г. , получено 16 декабря 2007 г.1954 год, 考古学家在位于长江中游地区的湖南省长沙左家公山发掘了一座距今两千一百多年的战国时期楚墓。墓中出土了一个竹筒,里面盛放着戥秤、砝码、毛笔以及四十余根长度约为十二厘米的竹片。这是最早发现也是最古的算筹实物。In Русский-В 1954 году археологи обнаружили гробницу династии Чу периода Воюющих царств, которой более 2100 лет, на горе Цзоцзягун в Чанше, провинция Хунань, в среднем течении реки Янцзы. В гробнице была обнаружена бамбуковая трубка, в которой находились весы, гири, щетка и более 40 бамбуковых кусков длиной около 12 см. Это самые ранние и самые старые обнаруженные счеты.
- ^ Математика Древнего Китая. Архивировано 26 января 2011 г. на Wayback Machine – Авторские права © 2010 – TutorVista.com, Все права защищены.
- ^ ВОНГ, Пуй Инь Марианна (март 2006 г.). «Силинг (четыре главных животных) в изобразительном искусстве Хань — том 1» (PDF) . SOAS : 370, 416.
- ^ "Блог BabelStone: Потерянная игра Любо. Часть 4: Игровые доски и оборудование". www.babelstone.co.uk . Получено 05.08.2020 .
- ^ Ред. У Вэньцзюнь, Большая серия истории китайской математики, т. 1, стр. 371
- ^ Лам, Лэй Юн; Анг, Тянь Сэ (2004). Мимолетные шаги: отслеживание концепции арифметики и алгебры в Древнем Китае. World Scientific. ISBN 978-981-256-725-3.
- ^ 孫子: 夫未戰而廟算勝者,得算多也
- ^ 老子: 善數者不用籌策。
- ^ Чжу, Ивэнь (2018). «Как западные письменные вычисления были введены в Китай? — Анализ «Тунвэнь суаньчжи» (Руководство по арифметике на общем языке, 1613)». ResearchGate . Получено 05.08.2020 .
- ^ Китайский викиисточник 孫子算經: 先識其位,一從十橫,百立千僵,千十相望,萬百相當。
- ^ Китайский Wikisource, 夢溪筆談: 如算法用赤籌、黑籌,以別正負之數。
- ^ abc Wáng, Qīngxiáng (1999), Sangi o koeta otoko (Человек, который превзошел счетные стержни) , Токио: Toyō Shoten, ISBN 4-88595-226-3
- ^ Китайский Wikisource 正負術曰:同名相除, 異名相益, 正無入負之, 負無入正之.其異名相除, 同名相益, 正無入正之, 負無入負之.
- ^ Карл Меннингер , Числовые слова и числовые символы, стр. 369, MIT Press, 1970
- ^ Аб Цянь, Баокун (1964), Чжунго Шусюэ Ши (История китайской математики) , Пекин: Кексюэ Чубанше
- ^ "Китайские цифры". История математики . Получено 28.04.2024 .
- ^ Кристофер Каллен и Джон Х. Дженкинс, Предложение добавить китайские счетные палочки в Unicode и ISO/IEC 10646, 2004
- ^ Стандарт Unicode, версия 5.0 – Электронное издание (PDF) , Unicode, Inc., 2006, стр. 558
- ^ Стандарт Unicode, версия 15.0 – Электронное издание (PDF) , Unicode , Inc., 2022, стр. 869–870
- ^ Стандарт Unicode, версия 5.0 – Электронное издание (PDF) , Unicode , Inc., 2006, стр. 499–500
Внешние ссылки
Для ознакомления с древними счетными палочками и получения дополнительных объяснений вы можете посетить сайты
- https://web.archive.org/web/20010217175749/http://www.math.sfu.ca/histmath/China/Beginning/Rod.html
- http://mathforum.org/library/drmath/view/52557.html
- Подсчет палочек в Китае (на китайском) ( Перевод на английский: Google, Bing, Yandex)
- Подсчет стержней и камней го японского математика около 1872 года (на японском языке) ( Перевод на английский: Google, Bing, Yandex)