Модель Рэмси – Касса – Купманса

Часть серии статей о
Макроэкономика
Основные понятия Совокупный спрос Совокупное предложение Деловой цикл CAGR Дефляция Demand shock Disinflation Effective demand Expectations Adaptive Rational Financial crisis Growth Inflation Demand-pull Cost-push Interest rate Investment Liquidity trap Measures of national income and output GDP GNI NNI Microfoundations Money Endogenous Money creation Demand for money Liquidity preference Money supply National accounts SNA Nominal rigidity Price level Recession Shrinkflation Stagflation Supply shock Saving Unemployment
Policies Fiscal Monetary Commercial Central bank Universal basic income
Models IS–LM AD–AS Keynesian cross Multiplier Accelerator Phillips curve Arrow–Debreu Harrod–Domar Solow–Swan Ramsey–Cass–Koopmans Overlapping generations General equilibrium DSGE Endogenous growth Matching theory Mundell–Fleming Overshooting NAIRU
Related fields Econometrics Economic statistics Monetary economics Development economics Evolutionary economics International economics
Schools Mainstream Keynesian Neo- New Monetarism New classical Real business-cycle theory Stockholm New neoclassical synthesis Saltwater and freshwater Heterodox Austrian Chartalism Modern monetary theory Ecological Post-Keynesian Circuitism Disequilibrium Marxian Market monetarism Supply-side
People François Quesnay Adam Smith Thomas Robert Malthus Karl Marx Léon Walras Knut Wicksell Irving Fisher Wesley Clair Mitchell John Maynard Keynes Alvin Hansen Michał Kalecki Gunnar Myrdal Simon Kuznets Joan Robinson Friedrich Hayek John Hicks Richard Stone Hyman Minsky Milton Friedman Paul Samuelson Lawrence Klein Edmund Phelps Robert Lucas Jr. Edward C. Prescott Peter Diamond William Nordhaus Joseph Stiglitz Thomas J. Sargent Paul Krugman N. Gregory Mankiw
See also Macroeconomic model Publications in macroeconomics Economics Applied Microeconomics Political economy Mathematical economics
Money portal Business portal
v t e

Модель Рэмси–Касса–Купманса , или модель роста Рэмси , является неоклассической моделью экономического роста, основанной в первую очередь на работе Фрэнка П. Рэмси 1928 года ^[1] со значительными расширениями Дэвида Касса и Тьяллинга Купманса в 1965 году. ^{[2] [3]} Модель Рэмси–Касса–Купманса отличается от модели Солоу–Свона тем, что выбор потребления явно микрообоснован в определенный момент времени и, таким образом, эндогенизирует норму сбережений . В результате, в отличие от модели Солоу–Свона, норма сбережений может не быть постоянной при переходе к долгосрочному устойчивому состоянию . Другим следствием модели является то, что результат является оптимальным по Парето или эффективным по Парето . ^{[примечание 1]}

Первоначально Рэмси определил модель как проблему социального планировщика по максимизации уровней потребления в течение последующих поколений. ^[4] Только позже модель была принята Кассом и Купмансом как описание децентрализованной динамической экономики с репрезентативным агентом . Модель Рэмси–Касса–Купманса нацелена только на объяснение долгосрочного экономического роста, а не колебаний делового цикла, и не включает в себя источники нарушений, такие как несовершенство рынка, неоднородность среди домохозяйств или экзогенные шоки . Последующие исследователи расширили модель, допустив государственные закупки, изменения занятости и другие шоки, в частности, в теории реального делового цикла .

В обычной установке время непрерывно, начинаясь, для простоты, в и продолжаясь вечно. По предположению, единственными производительными факторами являются капитал и труд , оба должны быть неотрицательными. Предполагается, что рабочая сила, которая составляет все население, растет с постоянной скоростью , т. е . , подразумевая, что при начальном уровне в . Наконец, пусть обозначает совокупное производство и обозначает совокупное потребление. ${\displaystyle t=0}$${\displaystyle K}$${\displaystyle L}$${\displaystyle n}$${\displaystyle {\dot {L}}={\tfrac {\mathrm {d} L}{\mathrm {d} t}}=nL}$${\displaystyle L=L_{0}e^{nt}}$${\displaystyle L_{0}>0}$${\displaystyle t=0}$${\displaystyle Y}$${\displaystyle C}$

Переменные, которые модель Рэмси-Касса-Купманса в конечном итоге стремится описать, — это потребление на душу населения (или, точнее, на труд ): и интенсивность капитала : Она делает это, связывая накопление капитала , записанное в нотации Ньютона , с потреблением , описывая компромисс между потреблением и инвестициями. Более конкретно, поскольку существующий основной капитал уменьшается по норме амортизации (предполагаемой постоянной), требуются инвестиции в объем производства текущего периода . Таким образом,$${\displaystyle c={\frac {C}{L}}}$$$${\displaystyle k={\frac {K}{L}}}$$${\displaystyle {\dot {K}}={\tfrac {\mathrm {d} K}{\mathrm {d} t}}}$${\displaystyle C}$${\displaystyle \delta }$${\displaystyle Y}$$${\displaystyle {\dot {K}}=Y-\delta K-cL}$$

Связь между производственными факторами и совокупным выпуском описывается совокупной производственной функцией , . Обычным выбором является производственная функция Кобба–Дугласа , но, как правило, допустима любая производственная функция, удовлетворяющая условиям Инады . Важно, однако, что требуется, чтобы была однородной степени 1 , что экономически подразумевает постоянную отдачу от масштаба . При таком предположении мы можем повторно выразить совокупный выпуск в расчете на душу населения . Например, если мы используем производственную функцию Кобба–Дугласа с , то .${\displaystyle Y=F(K,L)}$ ${\displaystyle F(K,L)=AK^{1-\alpha }L^{\alpha }}$${\displaystyle F}$$${\displaystyle F(K,L)=L\cdot F\left({\frac {K}{L}},1\right)=L\cdot f(k)}$$${\displaystyle A=1,\alpha =0.5}$${\displaystyle f(k)=k^{0.5}}$

Чтобы получить первое ключевое уравнение модели Рэмси–Касса–Купманса, динамическое уравнение для основного капитала должно быть выражено в терминах на душу населения . Отмечая правило частного для , мы имеем${\displaystyle {\tfrac {\mathrm {d} }{\mathrm {d} t}}\left({\tfrac {K}{L}}\right)}$

Нелинейное дифференциальное уравнение, родственное модели Солоу–Суона , но включающее эндогенное потребление 𝑐, отражающее микроосновы модели.

Если мы игнорируем проблему распределения потребления, то норма полезности является функцией совокупного потребления. То есть, . Чтобы избежать проблемы бесконечности, мы экспоненциально дисконтируем будущую полезность по ставке дисконтирования . Высокая отражает высокое нетерпение .${\displaystyle U}$${\displaystyle U=U(C,t)}$ ${\displaystyle \rho \in (0,\infty )}$${\displaystyle \rho }$

Задача социального планировщика — максимизация функции общественного благосостояния. Предположим, что экономика населена идентичными бессмертными индивидуумами с неизменными функциями полезности ( репрезентативный агент ), так что общая полезность равна: Предполагается, что функция полезности строго возрастает (т. е. нет точки блаженства ) и вогнута в , причем , ^{[примечание 2]} где — предельная полезность потребления . Таким образом, у нас есть задача социального планировщика:$${\displaystyle U_{0}=\int _{0}^{\infty }e^{-\rho t}U(C,t)\,\mathrm {d} t}$$${\displaystyle u(c)}$$${\displaystyle U(C,t)=Lu(c)=L_{0}e^{nt}u(c)}$$${\displaystyle c}$${\displaystyle \lim _{c\to 0}u_{c}=\infty }$${\displaystyle u_{c}}$${\displaystyle {\tfrac {\partial u}{\partial c}}}$

${\displaystyle \max _{c}\int _{0}^{\infty }e^{-(\rho -n)t}u(c)\,\mathrm {d} t}$

${\displaystyle {\text{subject to}}\quad c=f(k)-(n+\delta )k-{\dot {k}}}$

где задан начальный ненулевой капитальный запас . Чтобы гарантировать, что интеграл хорошо определен, мы накладываем . ${\displaystyle k(0)=k_{0}>0}$${\displaystyle \rho >n}$

Решение, обычно находимое с помощью функции Гамильтона , ^{[примечание 3] [примечание 4]} представляет собой дифференциальное уравнение, описывающее оптимальную эволюцию потребления,

Правило Кейнса -Рэмси . ^[5]

Термин , где — предельный продукт капитала , отражает предельную доходность чистых инвестиций с учетом амортизации капитала и дисконтирования по времени.${\displaystyle f_{k}(k)-\delta -\rho }$${\displaystyle f_{k}=\partial _{k}f}$

Вот эластичность межвременного замещения (EIS), определяемая как Она формально эквивалентна обратной величине относительного неприятия риска . Величина отражает кривизну функции полезности и указывает, насколько репрезентативный агент желает сгладить потребление с течением времени. Если у агента высокое относительное непринятие риска, у него низкий EIS, и поэтому он будет более склонен сглаживать потребление с течением времени.${\displaystyle \sigma (c)}$$${\displaystyle \sigma (c)=-{\frac {u_{c}(c)}{c\cdot u_{cc}(c)}}=-{\frac {d\ln c}{d\ln(u'(c))}}}$$

Часто предполагается, что строго монотонно возрастает и вогнута, таким образом . В частности, если полезность логарифмическая, то она постоянна: Мы можем переписать правило Рамсея как , где мы интерпретируем как «скорость задержки потребления», указывающую скорость, с которой текущее потребление откладывается в пользу будущего потребления. Более высокое значение подразумевает, что агент отдает приоритет сбережению, а не потреблению сегодня, тем самым откладывая потребление на более позднее время.${\displaystyle u}$${\displaystyle \sigma >0}$$${\displaystyle u(c)=u_{0}\ln c\implies \sigma (c)=1}$$$${\displaystyle \underbrace {{\frac {d}{dt}}\ln c} _{\text{consumption delay rate}}=\underbrace {\sigma (c)} _{{\text{EIS at current consumption level}}\quad }\underbrace {[f_{k}(k)-\delta -\rho ]} _{\text{marginal return on net investment}}}$$${\displaystyle {\frac {d}{dt}}\ln c}$

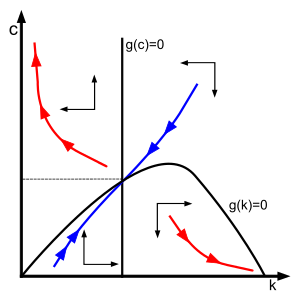
Два связанных дифференциальных уравнения для и образуют динамическую систему Рамсея–Касса–Купманса .${\displaystyle k}$${\displaystyle c}$

Устойчивое состояние системы находится путем установки и равным нулю. Существует три решения:${\displaystyle (k^{\ast },c^{\ast })}$${\displaystyle {\dot {k}}}$${\displaystyle {\dot {c}}}$

${\displaystyle f_{k}\left(k^{\ast }\right)=\delta +\rho \quad {\text{and}}\quad c^{\ast }=f\left(k^{\ast }\right)-(n+\delta )k^{\ast }}$

${\displaystyle (0,0)}$

${\displaystyle f(k^{*})=(n+\delta )k^{*}{\text{ with }}k^{*}>0,c^{*}=0}$

Первое — единственное решение внутри верхнего квадранта. Это седловая точка (как показано ниже). Второе — отталкивающая точка. Третье — вырожденное устойчивое равновесие. Первое решение подразумевается по умолчанию, хотя два других важно отслеживать.

Любая оптимальная траектория должна следовать динамической системе. Однако, поскольку переменная является управляющей переменной , при каждой интенсивности капитала , чтобы найти ее соответствующую оптимальную траекторию, нам все еще нужно найти ее начальную норму потребления . Как оказывается, оптимальная траектория является единственной, которая сходится к внутренней точке равновесия. Любая другая траектория либо сходится к всесберегающему равновесию с , либо расходится к , что означает, что экономика расходует весь свой капитал за конечное время. Оба достигают более низкой общей полезности, чем траектория к внутренней точке равновесия.${\displaystyle c}$${\displaystyle k}$${\displaystyle c(0)}$${\displaystyle k^{*}>0,c^{*}=0}$${\displaystyle k\to 0,c\to \infty }$

Качественное утверждение об устойчивости решения требует линеаризации полиномом Тейлора первого порядка.${\displaystyle (k^{\ast },c^{\ast })}$

${\displaystyle {\begin{bmatrix}{\dot {k}}\\{\dot {c}}\end{bmatrix}}\approx \mathbf {J} (k^{\ast },c^{\ast }){\begin{bmatrix}(k-k^{\ast })\\(c-c^{\ast })\end{bmatrix}}}$

где матрица Якоби оценивается в устойчивом состоянии, ^{[примечание 5]} задается формулой${\displaystyle \mathbf {J} (k^{\ast },c^{\ast })}$

${\displaystyle \mathbf {J} \left(k^{\ast },c^{\ast }\right)={\begin{bmatrix}\rho -n&-1\\{\frac {1}{\sigma }}f_{kk}(k)\cdot c^{\ast }&0\end{bmatrix}}}$

который имеет определитель, так как , является положительным по предположению, и поскольку является вогнутым (условие Инады). Поскольку определитель равен произведению собственных значений , собственные значения должны быть действительными и противоположными по знаку. ^[6]${\displaystyle \left|\mathbf {J} \left(k^{\ast },c^{\ast }\right)\right|={\frac {1}{\sigma }}f_{kk}(k)\cdot c^{\ast }<0}$${\displaystyle c^{*}>0}$${\displaystyle \sigma }$${\displaystyle f_{kk}<0}$${\displaystyle f}$

Следовательно, по теореме об устойчивом многообразии равновесие является седловой точкой , и существует единственный устойчивый рукав, или «седловой путь», который сходится к равновесию, обозначенному синей кривой на фазовой диаграмме.

Система называется «устойчивой седловой траекторией», поскольку все неустойчивые траектории исключаются условием «отсутствия схемы Понци »: ^[7]

${\displaystyle \lim _{t\to \infty }k\cdot e^{-\int _{0}^{t}\left(f_{k}-n-\delta \right)\mathrm {d} s}\geq 0}$

подразумевая, что текущая стоимость основного капитала не может быть отрицательной. ^{[примечание 6]}

This section has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. Find sources: "Ramsey–Cass–Koopmans model" – news · newspapers · books · scholar · JSTOR (December 2017) (Learn how and when to remove this message) This section possibly contains original research. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (December 2017) (Learn how and when to remove this message) This section may lend undue weight to certain ideas, incidents, or controversies. Please help improve it by rewriting it in a balanced fashion that contextualizes different points of view. (December 2017) (Learn how and when to remove this message) (Learn how and when to remove this message)

Спир и Янг пересматривают историю оптимального роста в 1950-х и 1960-х годах, ^[8] уделяя особое внимание правдивости заявленной одновременной и независимой разработки работы Касса «Оптимальный рост в агрегированной модели накопления капитала» (опубликованной в 1965 году в Review of Economic Studies ) и работы Тьяллинг Купмана «О концепции оптимального экономического роста» (опубликованной в Study Week on the Econometric Approach to Development Planning, 1965, Рим: Папская академия наук).

За всю свою жизнь ни Касс, ни Купманс никогда не предполагали, что их результаты, характеризующие оптимальный рост в модели роста с одним сектором и непрерывным временем, были чем-то иным, кроме как «одновременными и независимыми». Приоритетный вопрос стал предметом обсуждения, поскольку в опубликованной версии работы Купманса он процитировал главу из диссертации Касса, которая позже стала статьей RES . В своей статье Купманс в сноске утверждает, что Касс независимо получил условия, похожие на те, что он находит. Касс также рассматривает в своей статье предельный случай, когда ставка дисконтирования стремится к нулю. Со своей стороны, Касс отмечает, что «после того, как была завершена первоначальная версия этой статьи, наше внимание привлек очень похожий анализ Купманса. Мы опираемся на его результаты при обсуждении предельного случая, когда эффективная социальная ставка дисконтирования стремится к нулю». В интервью, которое Касс дал журналу Macroeconomic Dynamics , он приписывает Купмансу указание на предыдущую работу Фрэнка Рэмси, утверждая, что ему было стыдно не знать о ней, но не говорит ничего, что могло бы развеять основное утверждение о том, что его работа и работа Купманса были независимы.

Спир и Янг оспаривают эту историю, основываясь на ранее упущенной рабочей версии статьи Купманса, ^[9] которая была основой для часто цитируемой презентации Купманса на конференции, проведенной Папской академией наук в октябре 1963 года. ^[10] В этой статье обсуждения Коулза есть ошибка. Купманс утверждает в своем основном результате, что уравнения Эйлера являются как необходимыми, так и достаточными для характеристики оптимальных траекторий в модели, поскольку любые решения уравнений Эйлера, которые не сходятся к оптимальному стационарному состоянию, достигли бы либо нулевой границы потребления, либо нулевого капитала за конечное время. Эта ошибка была представлена ​​на конференции в Ватикане, хотя ни один участник не прокомментировал проблему во время презентации Купманса. Это можно вывести, поскольку обсуждение после каждой презентации статьи на конференции в Ватикане дословно приводится в томе конференции.

В обсуждении тома Ватикана после презентации статьи Эдмона Малинво этот вопрос действительно возникает из-за явного включения Малинво так называемого «условия трансверсальности» (которое Малинво называет Условием I) в свою статью. В конце презентации Купманс спрашивает Малинво, не гарантирует ли Условие I, что решения уравнений Эйлера, которые не сходятся к оптимальному стационарному состоянию, достигают границы за конечное время. Малинво отвечает, что это не так, и предлагает Купмансу рассмотреть пример с функциями логарифмической полезности и производственными функциями Кобба-Дугласа.

В этот момент Купманс осознает, что у него есть проблема. Однако, основываясь на запутанном приложении к более поздней версии статьи, выпущенной после Ватиканской конференции, он, похоже, не может решить, как справиться с вопросом, поднятым в Условии I Малинво.

Из интервью с Кассом в журнале Macroeconomic Dynamics становится ясно, что Купманс встречался с научным руководителем Касса Хирофуми Удзавой на зимних заседаниях Эконометрического общества в январе 1964 года, где Удзава сообщил ему, что его студент [Касс] уже решил эту проблему. Удзава, должно быть, затем предоставил Купмансу копию главы диссертации Касса, которую он послал под видом Технического отчета IMSSS, на который Купманс ссылался в опубликованной версии своей статьи. Слово «под видом» здесь уместно, поскольку номер TR, указанный в цитате Купманса, указал бы дату выпуска отчета на начало 1950-х годов, чего не было.

В опубликованной версии статьи Купманса он вводит новое Условие Альфа в дополнение к уравнениям Эйлера, утверждая, что единственной допустимой траекторией среди тех, которые удовлетворяют уравнениям Эйлера, является та, которая сходится к оптимальному стационарному равновесию модели. Этот результат выведен в статье Касса посредством наложения условия трансверсальности, которое Касс вывел из соответствующих разделов книги Льва Понтрягина . ^[11] Спир и Янг предполагают, что Купманс выбрал этот путь, потому что он не хотел показаться «заимствовавшим» технологию трансверсальности Малинво или Касса.

Основываясь на этом и других исследованиях вклада Малинво в 1950-х годах, в частности, на его интуитивном понимании важности условия трансверсальности, Спир и Янг предполагают, что неоклассическую модель роста лучше было бы назвать моделью Рэмси–Малинво–Касса, а не устоявшимся почетным наименованием Рэмси–Касса–Купманса.

• Асемоглу, Дарон (2009). «Неоклассическая модель роста». Введение в современный экономический рост . Принстон: Princeton University Press. стр.  287–326 . ISBN 978-0-691-13292-1.
• Барро, Роберт Дж.; Сала -и-Мартин, Ксавье (2004). «Модели роста с оптимизацией потребителей». Экономический рост (второе изд.). Нью-Йорк: McGraw-Hill. С.  85–142 . ISBN 978-0-262-02553-9.
• Бенасси, Жан-Паскаль (2011). «Модель Рамсея». Макроэкономическая теория . Нью-Йорк: Oxford University Press. С.  145–160 . ISBN 978-0-19-538771-1.
• Бланшар, Оливье Жан ; Фишер, Стэнли (1989). «Потребление и инвестиции: базовые модели с бесконечным горизонтом». Лекции по макроэкономике . Кембридж: MIT Press. стр.  37–89 . ISBN 978-0-262-02283-5.
• Мяо, Цзяньцзюнь (2014). «Неоклассические модели роста». Экономическая динамика в дискретном времени . Кембридж: MIT Press. стр.  353–364 . ISBN 978-0-262-02761-8.
• Новалес, Альфонсо; Фернандес, Эстер; Руис, Хесус (2009). «Оптимальный рост: непрерывный анализ времени». Экономический рост: теория и численные методы решения . Берлин: Springer. С.  101–154 . ISBN 978-3-540-68665-1.
• Ромер, Дэвид (2011). «Модели бесконечного горизонта и перекрывающихся поколений». Advanced Macroeconomics (четвертое изд.). Нью-Йорк: McGraw-Hill. С.  49–77 . ISBN 978-0-07-351137-5.

• Обсуждение оригинальной статьи Рэмси Орацио Аттанасио на YouTube