Подключение (основной пучок)

В математике , и особенно в дифференциальной геометрии и калибровочной теории , связность — это устройство, которое определяет понятие параллельного переноса на расслоении; то есть способ «соединить» или идентифицировать волокна над близлежащими точками. Главная G -связность на главном G-расслоении над гладким многообразием — это особый тип связности, совместимый с действием группы .${\displaystyle P}$ ${\displaystyle М}$${\displaystyle G}$

Главную связность можно рассматривать как частный случай понятия связности Эресмана , и иногда ее называют главной связностью Эресмана . Она порождает (Эресмановы) связности на любом расслоении волокон, связанном с посредством конструкции связанного расслоения . В частности, на любом связанном векторном расслоении главная связность индуцирует ковариантную производную — оператор, который может дифференцировать сечения этого расслоения вдоль касательных направлений в базовом многообразии. Главные связности обобщают на произвольные главные расслоения концепцию линейной связности на расслоении рамок гладкого многообразия .${\displaystyle P}$

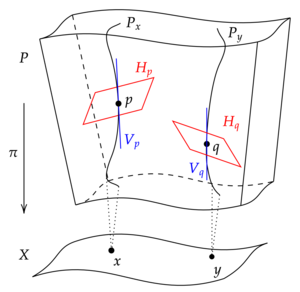
Пусть — гладкое главное G -расслоение над гладким многообразием . Тогда главная -связность на — это дифференциальная 1-форма на со значениями в алгебре Ли , которая является -эквивариантной и воспроизводит генераторы алгебры Ли фундаментальных векторных полей на .${\displaystyle \pi :P\to M}$ ${\displaystyle М}$ ${\displaystyle G}$${\displaystyle P}$${\displaystyle P}$ ${\displaystyle {\mathfrak {g}}}$${\displaystyle G}$${\displaystyle G}$${\displaystyle P}$

Другими словами, это элемент ω такой , что${\displaystyle \Omega ^{1}(P,{\mathfrak {g}})\cong C^{\infty }(P,T^{*}P\otimes {\mathfrak {g}})}$

1. ${\displaystyle {\hbox{Ad}}_{g}(R_{g}^{*}\omega )=\omega }$где обозначает правое умножение на , а — сопряженное представление на (явно, );${\displaystyle R_{g}}$${\displaystyle г}$${\displaystyle \operatorname {Ad} _{g}}$${\displaystyle {\mathfrak {g}}}$${\displaystyle \operatorname {Ad} _{g}X={\frac {d}{dt}}g\exp(tX)g^{-1}{\bigl |}_{t=0}}$
2. если и — векторное поле на P, связанное с ξ путем дифференцирования действия G на P , то (тождественно на ).${\displaystyle \xi \in {\mathfrak {g}}}$${\displaystyle X_{\xi }}$${\displaystyle \omega (X_{\xi })=\xi }$${\displaystyle P}$

Иногда термин «главная связь»${\displaystyle G}$ относится к паре и сам по себе называется формой связи или формой связи 1 главной связи.${\displaystyle (P,\omega )}$${\displaystyle \omega }$

Большинство известных нетривиальных вычислений главных -связностей выполняются с однородными пространствами из-за тривиальности (ко)касательного расслоения. (Например, пусть , будет главным -расслоением над .) Это означает, что 1-формы на тотальном пространстве канонически изоморфны , где - двойственная алгебра Ли, следовательно, -связности находятся во взаимной однозначности с .${\displaystyle G}$${\displaystyle G\to H\to H/G}$${\displaystyle G}$${\displaystyle H/G}$${\displaystyle C^{\infty }(H,{\mathfrak {g}}^{*})}$${\displaystyle {\mathfrak {g}}^{*}}$${\displaystyle G}$${\displaystyle C^{\infty }(H,{\mathfrak {g}}^{*}\otimes {\mathfrak {g}})^{G}}$

Главная -связность на определяет связность Эресмана на следующим образом. Сначала отметим, что фундаментальные векторные поля, порождающие действие на, обеспечивают изоморфизм расслоений (покрывающий тождество ) из расслоения в , где - ядро ​​касательного отображения , которое называется вертикальным расслоением . Отсюда следует, что однозначно определяет отображение расслоения , которое является тождеством на . Такая проекция однозначно определяется своим ядром, которое является гладким подрасслоением ( называемым горизонтальным расслоением ), таким что . Это связность Эресмана.${\displaystyle G}$${\displaystyle \omega }$${\displaystyle P}$${\displaystyle P}$${\displaystyle G}$${\displaystyle P}$${\displaystyle P}$ ${\displaystyle V}$${\displaystyle P\times {\mathfrak {g}}}$${\displaystyle V=\ker(d\pi )}$ ${\displaystyle {\mathrm {d} }\pi \colon TP\to TM}$${\displaystyle P}$${\displaystyle \omega }$${\displaystyle v:TP\rightarrow V}$${\displaystyle V}$${\displaystyle v}$${\displaystyle H}$${\displaystyle TP}$${\displaystyle TP=V\oplus H}$

Наоборот, связность Эресмана (или ) на определяет главную -связность тогда и только тогда, когда она является -эквивариантной в том смысле, что .${\displaystyle H\subset TP}$${\displaystyle v:TP\rightarrow V}$${\displaystyle P}$${\displaystyle G}$${\displaystyle \omega }$${\displaystyle G}$${\displaystyle H_{pg}=\mathrm {d} (R_{g})_{p}(H_{p})}$

Тривиализирующее сечение главного расслоения задается сечением s над открытым подмножеством . Тогда пулбэк s ^* ω главного соединения является 1-формой на со значениями в . Если сечение s заменить новым сечением sg , определяемым как ( sg )( x ) = s ( x ) g ( x ), где g : M → G — гладкое отображение, то . Главное соединение однозначно определяется этим семейством -значных 1-форм, и эти 1-формы также называются формами соединения или 1-формами соединения , особенно в старой или более ориентированной на физику литературе.${\displaystyle P}$${\displaystyle P}$${\displaystyle U}$${\displaystyle M}$ ${\displaystyle U}$${\displaystyle {\mathfrak {g}}}$${\displaystyle (sg)^{*}\omega =\operatorname {Ad} (g)^{-1}s^{*}\omega +g^{-1}dg}$${\displaystyle {\mathfrak {g}}}$

Группа действует на касательном расслоении правым переносом. Фактор-пространство TP / G также является многообразием и наследует структуру расслоения над TM , которое будет обозначаться dπ : TP / G → TM . Пусть ρ: TP / G → M — проекция на M . Слои расслоения TP / G при проекции ρ несут аддитивную структуру.${\displaystyle G}$ ${\displaystyle TP}$

Расслоение TP / G называется расслоением главных связностей (Kobayashi 1957). Сечение Γ dπ: TP / G → TM такое, что Γ : TM → TP / G является линейным морфизмом векторных расслоений над M , можно отождествить с главной связностью в P . Наоборот, главная связность, определенная выше, порождает такое сечение Γ TP / G .

Наконец, пусть Γ будет главной связностью в этом смысле. Пусть q : TP → TP / G будет фактор-картой. Горизонтальное распределение связности — это расслоение

${\displaystyle H=q^{-1}\Gamma (TM)\subset TP.}$Мы снова видим связь с горизонтальным пучком и, таким образом, связь Эресмана.

Если ω и ω ′ являются главными связями на главном расслоении P , то разность ω ′ − ω является -значной 1-формой на P , которая не только G -эквивариантна, но и горизонтальна в том смысле, что она обращается в нуль на любом сечении вертикального расслоения V расслоения P . Следовательно, она является базовой и поэтому определяется 1-формой на M со значениями в присоединенном расслоении${\displaystyle {\mathfrak {g}}}$

${\displaystyle {\mathfrak {g}}_{P}:=P\times ^{G}{\mathfrak {g}}.}$

Наоборот, любая такая форма определяет (посредством обратного образа) G -эквивариантную горизонтальную 1-форму на P , а пространство главных G -связностей является аффинным пространством для этого пространства 1-форм.

Для тривиального главного -расслоения , где , существует каноническая связность ^{[1] стр. 49}${\displaystyle G}$${\displaystyle \pi :E\to X}$${\displaystyle E=G\times X}$

${\displaystyle \omega _{MC}\in \Omega ^{1}(E,{\mathfrak {g}})}$

называется связью Маурера-Картана. Она определяется в точке${\displaystyle (g,x)\in G\times X}$

${\displaystyle (\omega _{MC})_{(g,x)}=(L_{g^{-1}}\circ \pi _{1})_{*}}$для${\displaystyle x\in X,g\in G}$

что является композицией

${\displaystyle T_{(g,x)}E\xrightarrow {\pi _{1*}} T_{g}G\xrightarrow {(L_{g^{-1}})_{*}} T_{e}G={\mathfrak {g}}}$

определение 1-формы. Обратите внимание, что

${\displaystyle \omega _{0}=(L_{g^{-1}})_{*}:T_{g}G\to T_{e}G={\mathfrak {g}}}$

— форма Маурера-Картана на группе Ли и .${\displaystyle G}$${\displaystyle \omega _{MC}=\pi _{1}^{*}\omega _{0}}$

Для тривиального главного -расслоения раздел идентичности, заданный как, определяет соответствие 1-1${\displaystyle G}$${\displaystyle \pi :E\to X}$${\displaystyle i:X\to G\times X}$${\displaystyle i(x)=(e,x)}$

${\displaystyle i^{*}:\Omega ^{1}(E,{\mathfrak {g}})\to \Omega ^{1}(X,{\mathfrak {g}})}$

между связями на и -значными 1-формами на ^{[1] стр. 53.} Для -значной 1-формы на существует единственная 1-форма на такая, что${\displaystyle E}$${\displaystyle {\mathfrak {g}}}$${\displaystyle X}$${\displaystyle {\mathfrak {g}}}$${\displaystyle A}$${\displaystyle X}$${\displaystyle {\tilde {A}}}$${\displaystyle E}$

1. ${\displaystyle {\tilde {A}}(X)=0}$для вертикального вектора${\displaystyle X\in T_{x}E}$
2. ${\displaystyle R_{g}^{*}{\tilde {A}}={\text{Ad}}(g^{-1})\circ {\tilde {A}}}$для любого${\displaystyle g\in G}$

Тогда, учитывая эту 1-форму, связь может быть построена путем взятия суммы${\displaystyle E}$

${\displaystyle \omega _{MC}+{\tilde {A}}}$

давая фактическое соединение на . Эта уникальная 1-форма может быть построена, сначала посмотрев на нее ограниченную для . Затем, определяется как , поскольку и мы можем получить , взяв${\displaystyle E}$${\displaystyle (e,x)}$${\displaystyle x\in X}$${\displaystyle {\tilde {A}}_{(e,x)}}$${\displaystyle A}$${\displaystyle T_{(x,e)}E=ker(\pi _{*})\oplus i_{*}T_{x}X}$${\displaystyle {\tilde {A}}_{(g,x)}}$

${\displaystyle {\tilde {A}}_{(g,x)}=R_{g}^{*}{\tilde {A}}_{(e,x)}={\text{Ad}}(g^{-1})\circ {\tilde {A}}_{(e,x)}}$

Аналогично, форма

${\displaystyle {\tilde {A}}_{(x,g)}={\text{Ad}}(g^{-1})\circ A_{x}\circ \pi _{*}:T_{(x,g)}E\to {\mathfrak {g}}}$

определяет 1-форму, дающую свойства 1 и 2, перечисленные выше.

Это утверждение можно уточнить ^{[1] стр. 55} еще больше для нетривиальных расслоений , рассмотрев открытое покрытие с тривиализациями и функциями перехода . Тогда существует соответствие 1-1 между связями на и наборами 1-форм${\displaystyle E\to X}$${\displaystyle {\mathcal {U}}=\{U_{a}\}_{a\in I}}$${\displaystyle X}$ ${\displaystyle \{\phi _{a}\}_{a\in I}}$${\displaystyle \{g_{ab}\}_{a,b\in I}}$${\displaystyle E}$

${\displaystyle \{A_{a}\in \Omega _{1}(U_{a},{\mathfrak {g}})\}_{a\in I}}$

которые удовлетворяют

${\displaystyle A_{b}=Ad(g_{ab}^{-1})\circ A_{a}+g_{ab}^{*}\omega _{0}}$

на пересечениях для формы Маурера-Картана на , в матричной форме.${\displaystyle U_{ab}}$${\displaystyle \omega _{0}}$${\displaystyle G}$${\displaystyle \omega _{0}=g^{-1}dg}$

Для главного расслоения множество связей в является аффинным пространством ^{[1] стр. 57} для векторного пространства , где — ассоциированное сопряженное векторное расслоение. Это подразумевает, что для любых двух связей существует форма такая, что${\displaystyle G}$${\displaystyle \pi :E\to M}$${\displaystyle E}$${\displaystyle \Omega ^{1}(M,E_{\mathfrak {g}})}$${\displaystyle E_{\mathfrak {g}}}$${\displaystyle \omega _{0},\omega _{1}}$${\displaystyle A\in \Omega ^{1}(M,E_{\mathfrak {g}})}$

${\displaystyle \omega _{0}=\omega _{1}+A}$

Обозначим набор связей как , или просто, если контекст ясен.${\displaystyle {\mathcal {A}}(E)}$${\displaystyle {\mathcal {A}}}$

Мы ^{[1] стр. 94} можем построить как главное -расслоение , где и - проекционное отображение${\displaystyle \mathbb {CP} ^{n}}$${\displaystyle \mathbb {C} ^{*}}$${\displaystyle \gamma :H_{\mathbb {C} }\to \mathbb {CP} ^{n}}$${\displaystyle H_{\mathbb {C} }=\mathbb {C} ^{n+1}-\{0\}}$${\displaystyle \gamma }$

${\displaystyle \gamma (z_{0},\ldots ,z_{n})=[z_{0},\ldots ,z_{n}]}$

Обратите внимание, что алгебра Ли — это просто комплексная плоскость. 1-форма определяется как${\displaystyle \mathbb {C} ^{*}=GL(1,\mathbb {C} )}$${\displaystyle \omega \in \Omega ^{1}(H_{\mathbb {C} },\mathbb {C} )}$

${\displaystyle {\begin{aligned}\omega &={\frac {{\overline {z}}^{t}dz}{|z|^{2}}}\\&=\sum _{i=0}^{n}{\frac {{\overline {z}}_{i}}{|z|^{2}}}dz_{i}\end{aligned}}}$

образует связь, которую можно проверить, проверив определение. Для любого фиксированного мы имеем${\displaystyle \lambda \in \mathbb {C} ^{*}}$

${\displaystyle {\begin{aligned}R_{\lambda }^{*}\omega &={\frac {{\overline {(z\lambda )}}^{t}d(z\lambda )}{|z\lambda |^{2}}}\\&={\frac {{\overline {\lambda }}\lambda {\overline {z}}^{t}dz}{|\lambda |^{2}\cdot |z|^{2}}}\end{aligned}}}$

и поскольку , то мы имеем -инвариантность. Это потому, что сопряженное действие тривиально, поскольку алгебра Ли абелева. Для построения расщепления, заметим, что для любого у нас есть короткая точная последовательность${\displaystyle |\lambda |^{2}={\overline {\lambda }}{\lambda }}$${\displaystyle \mathbb {C} ^{*}}$${\displaystyle z\in H_{\mathbb {C} }}$

${\displaystyle 0\to \mathbb {C} \xrightarrow {v_{z}} T_{z}H_{\mathbb {C} }\xrightarrow {\gamma _{*}} T_{[z]}\mathbb {CP} ^{n}\to 0}$

где определяется как${\displaystyle v_{z}}$

${\displaystyle v_{z}(\lambda )=z\cdot \lambda }$

поэтому он действует как масштабирование в волокне (которое ограничивается соответствующим -действием). Принимая, мы получаем${\displaystyle \mathbb {C} ^{*}}$${\displaystyle \omega _{z}\circ v_{z}(\lambda )}$

${\displaystyle {\begin{aligned}\omega _{z}\circ v_{z}(\lambda )&={\frac {{\overline {z}}dz}{|z|^{2}}}(z\lambda )\\&={\frac {{\overline {z}}z\lambda }{|z|^{2}}}\\&=\lambda \end{aligned}}}$

где второе равенство следует из того, что мы рассматриваем вертикальный касательный вектор, и . Обозначения несколько запутанны, но если мы разложим каждый член${\displaystyle z\lambda }$${\displaystyle dz(z\lambda )=z\lambda }$

${\displaystyle {\begin{aligned}dz&=dz_{0}+\cdots +dz_{n}\\z&=a_{0}z_{0}+\cdots +a_{n}z_{n}\\dz(z)&=a_{0}+\cdots +a_{n}\\dz(\lambda z)&=\lambda \cdot (a_{0}+\cdots +a_{n})\\{\overline {z}}&={\overline {a_{0}}}+\cdots +{\overline {a_{n}}}\end{aligned}}}$

становится более ясно (где ).${\displaystyle a_{i}\in \mathbb {C} }$

Для любого линейного представления W группы G существует ассоциированное векторное расслоение над M , и главная связность индуцирует ковариантную производную на любом таком векторном расслоении. Эту ковариантную производную можно определить, используя тот факт, что пространство сечений над M изоморфно пространству G -эквивариантных W -значных функций на P . В более общем случае пространство k -форм со значениями в отождествляется с пространством G -эквивариантных и горизонтальных W -значных k -форм на P . Если α является такой k -формой, то ее внешняя производная d α , хотя и G -эквивариантна, больше не является горизонтальной. Однако комбинация d α + ω Λ α является таковой. Это определяет внешнюю ковариантную производную d ^ω от -значных k -форм на M до -значных ( k +1) -форм на M . В частности, когда k = 0, мы получаем ковариантную производную на .${\displaystyle P\times ^{G}W}$${\displaystyle P\times ^{G}W}$ ${\displaystyle P\times ^{G}W}$${\displaystyle P\times ^{G}W}$${\displaystyle P\times ^{G}W}$${\displaystyle P\times ^{G}W}$

Форма кривизны главной G -связности ω — это -значная 2-форма Ω, определяемая соотношением${\displaystyle {\mathfrak {g}}}$

${\displaystyle \Omega =d\omega +{\tfrac {1}{2}}[\omega \wedge \omega ].}$

Он является G -эквивариантным и горизонтальным, следовательно, соответствует 2-форме на M со значениями в . Отождествление кривизны с этой величиной иногда называют вторым структурным уравнением (Картана) . ^[2] Исторически возникновение структурных уравнений обнаружено в развитии связности Картана . При транспонировании в контекст групп Ли структурные уравнения известны как уравнения Маурера–Картана : это те же самые уравнения, но в другой постановке и обозначении.${\displaystyle {\mathfrak {g}}_{P}}$

Мы говорим, что связность плоская, если ее форма кривизны . Существует полезная характеристика главных расслоений с плоскими связями; то есть, главное -расслоение имеет плоскую связность ^{[1] стр. 68} тогда и только тогда, когда существует открытое покрытие с тривиализациями, такое, что все функции перехода${\displaystyle \omega }$${\displaystyle \Omega =0}$${\displaystyle G}$${\displaystyle \pi :E\to X}$${\displaystyle \{U_{a}\}_{a\in I}}$${\displaystyle \left\{\phi _{a}\right\}_{a\in I}}$

${\displaystyle g_{ab}:U_{a}\cap U_{b}\to G}$

являются постоянными. Это полезно, поскольку дает рецепт построения плоских главных -расслоений над гладкими многообразиями; а именно, беря открытое покрытие и определяя тривиализации с постоянными функциями перехода.${\displaystyle G}$

Если главное расслоение P является расслоением рамок или (в более общем случае) если оно имеет форму припоя , то связь является примером аффинной связи , а кривизна не является единственным инвариантом, поскольку следует учитывать дополнительную структуру формы припоя θ , которая является эквивариантной R ⁿ -значной 1-формой на P. В частности, форма кручения на P является R ⁿ -значной 2-формой Θ, определяемой соотношением

${\displaystyle \Theta =\mathrm {d} \theta +\omega \wedge \theta .}$

Θ является G -эквивариантным и горизонтальным, и поэтому он спускается до касательнозначной 2-формы на M , называемой кручением . Это уравнение иногда называют первым структурным уравнением (Картана) .

Если X является схемой (или, в более общем смысле, стеком, производным стеком или даже предварительным стеком), мы можем связать с ней так называемый стек де Рама , обозначаемый X _dR . Он обладает тем свойством, что главное расслоение G над X _dR является тем же самым, что и расслоение G с *плоской* связностью над X .

• Кобаяси, Сёсичи (1957), «Теория связей», Ann. Mat. Pura Appl. , 43 : 119–194 , doi : 10.1007/BF02411907 , S2CID  120972987
• Кобаяси, Сёсичи; Номидзу, Кацуми (1996), Основы дифференциальной геометрии , т. 1 (новое издание), Wiley Interscience , ISBN 0-471-15733-3
• Коларж, Иван; Михор, Петер; Словак, Ян (1993), Естественные операции в дифференциальной геометрии (PDF) , Springer-Verlag, архивировано из оригинала (PDF) 2017-03-30 , извлечено 2008-03-25