Всеусеченный многогранник
В геометрии всеусеченный многогранник — это усеченный квазиправильный многогранник . При их чередовании получаются плосконосые многогранники .
Все всеусеченные многогранники рассматриваются как зоноэдры . Они имеют символ Витхоффа p qr | и вершинные фигуры 2p.2q.2r .
В более общем смысле, всеусеченный многогранник — это оператор скоса в нотации многогранников Конвея .
Список выпуклых всеусеченных многогранников
Существуют три выпуклые формы . Эти формы можно рассматривать как красные грани одного правильного многогранника, желтые или зеленые грани двойственного многогранника и синие грани в усеченных вершинах квазиправильного многогранника.
Символ Вайтхоффа pqr | | Всеусеченный многогранник | Правильные/квазиправильные многогранники |
|---|---|---|
| 3 3 2 | |  Усеченный октаэдр      |    Тетраэдр / Октаэдр / Тетраэдр |
| 4 3 2 | | 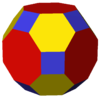 Усеченный кубооктаэдр      |    Куб / Кубооктаэдр / Октаэдр |
| 5 3 2 | |  Усеченный икосододекаэдр      |    Додекаэдр / Икосододекаэдр / Икосаэдр |
Список невыпуклых всеусеченных многогранников
Имеется 5 невыпуклых однородных всеусеченных многогранников.
Символ Вайтхоффа pqr | | Всеусеченный звездчатый многогранник | Символ Вайтхоффа pqr | | Всеусеченный звездчатый многогранник |
|---|---|---|---|
| Домены прямоугольного треугольника (r=2) | Общие треугольные домены | ||
| 3 4/3 2 | |  Большой усеченный кубооктаэдр        | 4 4/3 3 | |  Кубикоусеченный кубооктаэдр |
| 3 5/3 2 | |  Большой усеченный икосододекаэдр        | 5 5/3 3 | |  Икосекоративный додекододекаэдр |
| 5 5/3 2 | |  Усеченный додекадодекаэдр        | ||
Другие четносторонние невыпуклые многогранники
Существует 8 невыпуклых форм со смешанными символами Витхоффа p q (r s) | , и вершинными фигурами в форме галстука-бабочки , 2p.2q.-2q.-2p. Они не являются истинными всеусеченными многогранниками. Вместо этого истинные всеусеченные многогранники pqr | или pqs | имеют совпадающие 2 r -угольные или 2 s -угольные грани, которые должны быть удалены соответственно, чтобы сформировать правильный многогранник. Все эти многогранники являются односторонними, т. е. неориентируемыми . Вырожденные символы Витхоффа p q r | перечислены первыми, за ними следуют фактические смешанные символы Витхоффа.
| Всеусеченный многогранник | Изображение | Символ Витхоффа |
|---|---|---|
| Кубогемиоктаэдр |  | 3/2 2 3 | 2 3 (3/2 3/2) | |
| Малый ромбогексаэдр |  | 3/2 2 4 | 2 4 (3/2 4/2) | |
| Большой ромбогексаэдр |  | 4/3 3/2 2 | 2 4/3 (3/2 4/2) | |
| Малый ромбододекаэдр |  | 2 5/2 5 | 2 5 (3/2 5/2) | |
| Малый додекоикосаэдр |  | 3/2 3 5 | 3 5 (3/2 5/4) | |
| Ромбокосаэдр |  | 2 5/2 3 | 2 3 (5/4 5/2) | |
| Большой додекоикосаэдр |  | 5/2 5/3 3 | 3 5/3 (3/2 5/2) | |
| Большой ромбододекаэдр |  | 3/2 5/3 2 | 2 5/3 (3/2 5/4) | |
Общие обрезания (скосы)
Omnitruncations также называются cantitruncations или truncated rectifications (tr), и оператором Conway's bevel (b). При применении к нерегулярным многогранникам могут быть созданы новые многогранники, например, эти 2-однородные многогранники:
| Коксетер | trrC | тррД | trtT | trtC | trtO | trtI |
|---|---|---|---|---|---|---|
| Конвей | баО | плохой | бтТ | btc | бтО | бтИ |
| Изображение |  |  |  | 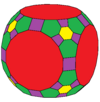 | 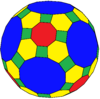 | 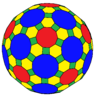 |
Смотрите также
Ссылки
- Коксетер, Гарольд Скотт Макдональд ; Лонге-Хиггинс, М.С.; Миллер, JCP (1954), «Однородные многогранники», Philosophical Transactions of the Royal Society of London. Серия A. Математические и физические науки , 246 (916): 401– 450, Bibcode : 1954RSPTA.246..401C, doi : 10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183
- Веннингер, Магнус (1974). Модели многогранников . Cambridge University Press. ISBN 0-521-09859-9.
- Скиллинг, Дж. (1975), «Полный набор однородных многогранников», Philosophical Transactions of the Royal Society of London. Серия A. Математические и физические науки , 278 (1278): 111– 135, Bibcode : 1975RSPTA.278..111S, doi : 10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333, S2CID 122634260
- Har'El, Z. Uniform Solution for Uniform Polyhedras., Geometriae Dedicata 47, 57-110, 1993. Zvi Har'El, программное обеспечение Kaleido, изображения, двойные изображения
- Мэдер Р.Э. Равномерные многогранники. Математика Дж. 3, 48–57, 1993.
| Семя | Усечение | Исправление | Бит-усечение | Двойной | Расширение | Omnitrcation (Обрезание) | Чередования | ||
|---|---|---|---|---|---|---|---|---|---|
     |      |      |      |      |      |      |      |      |      |
 |  |  |  |  |  |  |  |  |  |
| т 0 { п , д } { п , д } | т 01 { п , д } т { п , д } | т 1 { п , д } р { п , д } | т 12 { п , д } 2т { п , д } | т 2 { п , д } 2r{ п , д } | т 02 { п , д } рр{ п , д } | t012{p,q} tr{ p , q } | ht 0 { p , q } h{ q , p } | ht 12 { п , д } с { д , п } | ht 012 { п , д } ср { п , д } |