Электромагнитная реверберационная камера

Электромагнитная реверберационная камера (также известная как реверберационная камера (RVC) или камера с перемешиванием мод (MSC) ) — это среда для испытаний на электромагнитную совместимость (ЭМС) и других электромагнитных исследований. Электромагнитные реверберационные камеры были впервые представлены HA Mendes в 1968 году. [1] Реверберационная камера — это экранированное помещение с минимальным поглощением электромагнитной энергии . Благодаря низкому поглощению можно достичь очень высокой напряженности поля при умеренной входной мощности. Реверберационная камера — это объемный резонатор с высоким коэффициентом добротности . Таким образом, пространственное распределение напряженностей электрического и магнитного полей сильно неоднородно ( стоячие волны ). Для уменьшения этой неоднородности используются один или несколько тюнеров ( мешалок ). Тюнер — это конструкция с большими металлическими отражателями, которые можно перемещать в разных направлениях для достижения различных граничных условий . Самая низкая используемая частота (LUF) реверберационной камеры зависит от размера камеры и конструкции тюнера. Маленькие камеры имеют более высокий LUF, чем большие камеры.
Концепцию реверберационной камеры можно сравнить с микроволновой печью .
Глоссарий/обозначения
Предисловие
Обозначения в основном такие же, как в стандарте IEC 61000-4-21. [2] Для статистических величин, таких как средние и максимальные значения, используется более явное обозначение, чтобы подчеркнуть используемый домен. Здесь пространственный домен (индекс ) означает, что величины берутся для разных положений камеры, а ансамблевый домен (индекс ) относится к разным граничным или возбуждающим условиям (например, положениям тюнера).
Общий
- : Вектор электрического поля .
- : Вектор магнитного поля .
- : Общая напряженность электрического или магнитного поля , т. е. величина вектора поля .
- : Напряженность поля ( величина ) одной прямоугольной компоненты вектора электрического или магнитного поля .
- : Характеристическое сопротивление свободного пространства
- : Эффективность передающей антенны
- : Эффективность приемной антенны
- : Мощность бегущих вперед и назад волн .
- : Фактор качества .
Статистика
- : пространственное среднее для объектов (положений в пространстве).
- : среднее значение ансамбля для объектов (границ, т.е. положений тюнера).
- : эквивалентно . Это ожидаемое значение в статистике .
- : пространственный максимум для объектов (положений в пространстве).
- : максимум ансамбля для объектов (границ, т.е. положений тюнера).
- : эквивалентно .
- : отношение максимального значения к среднему в пространственной области.
- : отношение максимального значения к среднему в ансамблевой области.
Теория
Полостной резонатор
Реверберационная камера — это резонатор полости (обычно экранированная комната), который работает в сверхмодовой области. Чтобы понять, что это значит, нам нужно кратко рассмотреть резонаторы полости .
Для прямоугольных полостей резонансные частоты (или собственные частоты , или собственные частоты ) определяются как
где — скорость света , , и — длина, ширина и высота полости, а , , — неотрицательные целые числа (максимум одно из них может быть равно нулю ).
С помощью этого уравнения можно подсчитать количество мод с собственной частотой, меньшей заданного предела , . Это приводит к ступенчатой функции . В принципе, для каждой собственной частоты существуют две моды — поперечная электрическая мода и поперечная магнитная мода .
Поля в положении камеры определяются как
- для режимов ТМ ( )
- для TE-мод ( )
Из-за граничных условий для полей E и H некоторые моды не существуют. Ограничения следующие: [3]
- Для режимов TM: m и n не могут быть равны нулю, p может быть равен нулю
- Для TE-мод: m или n могут быть равны нулю (но не оба могут быть равны нулю), p не может быть равен нулю
Гладкая аппроксимация , , задается выражением
Главный член пропорционален объему камеры и третьей степени частоты . Этот член идентичен формуле Вейля .
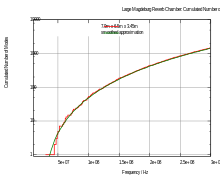
На основе плотности мод определяется выражением
Важной величиной является число мод в определенном частотном интервале , которое определяется выражением
Фактор качества
Фактор качества (или Q-фактор) является важной величиной для всех резонансных систем. Обычно Q-фактор определяется тем , где максимум и среднее значение берутся за один цикл, и является угловой частотой .
Фактор Q мод TE и TM можно рассчитать из полей. Сохраненная энергия определяется как
Потери происходят в металлических стенках. Если электропроводность стенки равна , а ее проницаемость равна , то поверхностное сопротивление равно
где - глубина проникновения материала стены.
Потери рассчитываются по формуле
Для прямоугольной полости следует [4]
- для TE-мод:
- для режимов ТМ:
Используя значения Q отдельных мод, можно вывести усредненный составной коэффициент качества : [5]
включает только потери из-за конечной проводимости стенок камеры и, следовательно, является верхним пределом. Другие потери — это диэлектрические потери, например, в опорных конструкциях антенны, потери из-за покрытий стен и потери утечки. Для нижнего диапазона частот доминирующие потери обусловлены антенной, используемой для связи энергии с помещением (передающая антенна, Tx) и для контроля полей в камере (приемная антенна, Rx). Эти потери антенны определяются как , где — количество антенн в камере.
Коэффициент качества, включающий все потери, представляет собой гармоническую сумму коэффициентов для всех отдельных процессов потерь:
В результате конечной добротности собственные моды расширяются по частоте, т.е. мода может быть возбуждена, даже если рабочая частота не совпадает точно с собственной частотой. Таким образом, для данной частоты возбуждается больше собственных мод в одно и то же время.
Q-полоса пропускания — это мера полосы пропускания частот, в которой коррелируются моды в реверберационной камере. Q реверберационной камеры можно рассчитать с помощью следующего:
Используя формулу, число возбужденных мод в результате будет равно
С коэффициентом качества камеры связана постоянная времени камеры :
Это постоянная времени релаксации свободной энергии поля камеры (экспоненциальный спад) при отключении входной мощности.
Смотрите также
Примечания
- ^ Мендес, HA: Новый подход к измерениям напряженности электромагнитного поля в экранированных корпусах. , Wescon Tech. Papers, Лос-Анджелес, Калифорния, август 1968 г.
- ^ IEC 61000-4-21: Электромагнитная совместимость (ЭМС) – Часть 4-21: Методы испытаний и измерений – Методы испытаний в реверберационной камере , Ред. 2.0, январь 2011 г. ([1])
- ^ Ченг, Д.К.: Полевые и волновые электромагнетики , Addison-Wesley Publishing Company Inc., издание 2, 1998. ISBN 0-201-52820-7
- ^ Чанг, К.: Справочник по микроволновым и оптическим компонентам , том 1, John Wiley & Sons Inc., 1989. ISBN 0-471-61366-5 .
- ^ Лю, Б. Х., Чанг, Д. К., Ма, М. Т.: Собственные моды и составной коэффициент качества реверберационной камеры , Техническая записка NBS 1066, Национальное бюро стандартов, Боулдер, Колорадо, август 1983 г.
Ссылки
- Кроуфорд, М. Л.; Кёпке, Г. Х.: Проектирование, оценка и использование реверберационной камеры для проведения измерений электромагнитной восприимчивости/уязвимости , Техническая записка NBS 1092, Национальное бюро стандартов, Боулдер, Колорадо, апрель 1986 г.
- Лэдбери, Дж. М.; Кёпке, Г. Х.: Взаимосвязи в реверберационной камере: исправления и улучшения, или три ошибки могут (почти) привести к истине , Электромагнитная совместимость, 1999 г., Международный симпозиум IEEE по теме, том 1, 1–6, 2–6 августа 1999 г.



















































































