календарь майя
Календарь, использовавшийся в доколумбовой Мезоамерике

Эта статья является частью серии статей на тему
цивилизация майя
Рисунок резьбы по камню майя с изысканным декором.
История
Испанское завоевание майя

Календарь майя — это система календарей, использовавшаяся в доколумбовой Мезоамерике и во многих современных общинах в горных районах Гватемалы , [1] Веракрусе , Оахаке и Чьяпасе , Мексика. [2]

Основы календаря майя основаны на системе, которая была в общем использовании во всем регионе, начиная с по крайней мере 5 века до н. э. Он разделяет многие аспекты с календарями, используемыми другими ранними цивилизациями Мезоамерики, такими как сапотеки и ольмеки , а также современными или более поздними, такими как календари миштеков и ацтеков . [3]

Согласно мифологической традиции майя , задокументированной в колониальных юкатекских источниках и реконструированной на основе позднеклассических и постклассических надписей, божество Ицамна часто приписывается предкам майя, принесшим им знание календарной системы, а также письменности в целом и других основополагающих аспектов культуры майя. [4]

Обзор

Календарь майя состоит из нескольких циклов или отсчетов разной длины. 260-дневный счет известен ученым как Tzolkin или Tzolkʼin . [5] Tzolkin был объединен с 365-дневным неопределенным солнечным годом, известным как Haabʼ, чтобы сформировать синхронизированный цикл, длящийся 52 Haabʼ, называемый Calendar Round . Calendar Round все еще используется многими группами в горных районах Гватемалы. [6]

Другой календарь использовался для отслеживания более длительных периодов времени и для записи календарных дат (т. е. для определения того, когда одно событие произошло по отношению к другим). Это Длинный счет . Это счет дней с мифологической отправной точки. [7] Согласно корреляции между Длинным счетом и западными календарями, принятой подавляющим большинством исследователей майя (известной как корреляция Гудмана-Мартинеса-Томпсона, или GMT), эта отправная точка эквивалентна 11 августа 3114 г. до н. э. в пролептическом григорианском календаре или 6 сентября в юлианском календаре (−3113 астрономический). Корреляция с GMT была выбрана Джоном Эриком Сидни Томпсоном в 1935 году на основе более ранних корреляций Джозефа Гудмена в 1905 году (11 августа), Хуана Мартинеса Эрнандеса в 1926 году (12 августа) и самого Томпсона в 1927 году (13 августа). [8] Благодаря своей линейной природе Длинный счет мог быть расширен для обозначения любой даты далеко в прошлом или будущем. Этот календарь включал использование позиционной системы обозначений, в которой каждая позиция обозначала увеличивающееся кратное количество дней. Система исчисления майя была по сути двадцатеричной (т. е. с основанием -20), и каждая единица данной позиции представляла собой 20-кратную единицу позиции, которая ей предшествовала. Важное исключение было сделано для разряда второго порядка, который вместо этого представлял 18 × 20, или 360 дней, более точно приближаясь к солнечному году, чем 20 × 20 = 400 дней. Циклы Длинного счета не зависят от солнечного года.

Многие надписи майя, написанные по методу Длинного счета, содержат дополнительную серию, которая содержит информацию о лунной фазе , номере текущего лунного месяца в серии из шести и о том, какой из девяти Владык Ночи правит.

Менее распространенные или плохо понятые циклы, комбинации и календарные прогрессии также отслеживались. 819-дневный счет засвидетельствован в нескольких надписях. Также известны повторяющиеся наборы из 9 дней (см. ниже «Девять владык ночи») [9] , связанные с различными группами божеств , животных и другими значимыми концепциями.

Цолькин

Tzolkʼin (в современной орфографии майя ; также обычно пишется tzolkin ) — название, которое исследователи майя обычно используют для обозначения Священного круга майя или 260-дневного календаря. Слово tzolkʼin — это неологизм, придуманный в юкатекском языке майя и означающий «счет дней» (Coe 1992). Различные названия этого календаря, используемые доколумбовыми майя, до сих пор являются предметом споров среди ученых. Эквивалент ацтекского календаря назывался Tōnalpōhualli на языке науатль .

Календарь цолкин объединяет двадцать названий дней с тринадцатью номерами дней, чтобы получить 260 уникальных дней. Он используется для определения времени религиозных и церемониальных событий, а также для гадания. Каждый последующий день нумеруется от 1 до 13, а затем снова начинается с 1. Отдельно от этого, каждому дню дается название в последовательности из списка из 20 названий дней:

Календарь Цолькин: названные дни и связанные с ними глифы

Номер последовательности 1		День
Имя 2
Пример глифа 3		16-й век
Юкатек 4		КичеРеконструированная
классическая майя 5
Номер последовательности 1		День
Имя 2
Пример глифа 3		16-й век
Юкатек 4		КичеРеконструированная
классическая майя 5
01ИмиксИмиксИмоксИмикс (?) / Ха' (?)11ЧувэньЧуэньБац(неизвестный)
02Ик'ИкIqʼИк'12Эб'ЭбЭ`(неизвестный)
03Акб'алАкбалАкабальАкб'ал (?)13Бен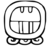БенАджC'klab [ требуется разъяснение ]
04К'анКанК'атКан (?)14ИксИксИкс, БаламХикс (?)
05ЧикчанЧикчанКан(неизвестный)15МужчиныМужчиныЦикинМужчины (?) [10]
06КимиЧимиКамеЧам (?)16Ки́бСибАджмак(неизвестный)
07МаникʼМаникКейМанич (?)17КабанКабанНо'джХаб (?)
08ЛаматЛаматQ'anilЭк (?)18ЭцнабЭцнабТиджакс(неизвестный)
09МулукМулукТодж(неизвестный)19КавакКауакКавок(неизвестный)
10ХорошоОкЦи(неизвестный)20АджоАхауАджпуАджо
ПРИМЕЧАНИЯ:
  1. Порядковый номер названного дня в календаре Цолькин
  2. Название дня недели в стандартизированной и пересмотренной орфографии Гватемальской академии языка майя [5]
  3. Пример глифа ( логограммы ) для названного дня. Обратите внимание, что для большинства из них записано несколько различных форм; те, что показаны здесь, типичны для резных монументальных надписей (это версии « картуша »)
  4. Название дня, записанное в записях майя-юкатеков XVI века , в основном Диего де Ланда ; эта орфография (до недавнего времени) широко использовалась
  5. В большинстве случаев фактическое название дня, как оно произносилось во времена классического периода (ок. 200–900), когда было сделано большинство надписей, неизвестно. Версии, приведенные здесь (на классическом языке майя , основном языке надписей), реконструированы на основе фонологических данных, если таковые имеются; символ «?» указывает на то, что реконструкция является предварительной. [11]

Некоторые системы начинали отсчет с 1 Imix, за которым следовали 2 Ikʼ, 3 Akʼbʼal и т. д. до 13 Bʼen. Затем номера дней снова начинаются с 1, в то время как последовательность названных дней продолжается, поэтому следующие дни в последовательности — 1 Ix, 2 Men, 3 Kʼibʼ, 4 Kabʼan, 5 Etzʼnabʼ, 6 Kawak и 7 Ajaw. При использовании всех двадцати названных дней они теперь начали повторять цикл, в то время как последовательность чисел продолжается, поэтому следующий день после 7 Ajaw — это 8 Imix. Таким образом, повторение этих взаимосвязанных 13- и 20-дневных циклов занимает 260 дней (то есть, чтобы каждая возможная комбинация числа/названного дня произошла один раз).

Самая ранняя известная надпись с цолкином — это ольмекская ушная катушка с 2 Ахау 3 Цех — 6.3.10.9.0, 2 сентября -678 г. (по юлианскому астрономическому календарю). [12]

Хааб

Месяцы Хааб : названия и глифы [13] в последовательности

Номер последовательности .		Юкатекское
название		Иероглиф
Классический период

знак глифа

Значение глифа
[14]		Реконструкция классических майя
1Поп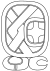𝋠к'анджало
2Woʼ𝋠икат
3Глоток𝋠чакат
4Соц𝋠летучая мышьсоц'
5Сек𝋠касиев
6Ксул𝋠чикин
7Якск'ин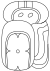𝋠yaxk'in
8Мол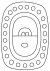𝋠моль
9Чэнь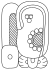𝋠черный [15]ик'сихо'м
10Якс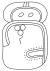𝋠зеленый [15]yaxsiho'm
11Сак𝋠белый [15]сакшихо'м
12Кех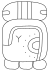𝋠красный [15]чаксихо'м
13Мак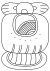𝋠мак
14Канкин𝋠униив
15Муван𝋠муван
16Пакс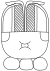𝋠паксиил
17Каяб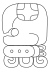𝋠к'анасий
18Кумку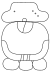𝋠охл
19Вайеб𝋠пять неудачных днейwayhaab

Хааб состоял из восемнадцати месяцев по двадцать дней каждый плюс период из пяти дней («безымянные дни») в конце года, известный как Вайеб (или Уайеб в орфографии XVI века). Пять дней Вайеба считались опасным временем. Фостер (2002) пишет: «Во время Вайеба порталы между миром смертных и подземным миром растворялись. Никакие границы не мешали злонамеренным божествам вызывать бедствия». Чтобы отогнать этих злых духов, у майя были обычаи и ритуалы, которые они практиковали во время Вайеба. Например, люди избегали выходить из домов и мыть или расчесывать волосы. Брикер (1982) подсчитал, что Хааб впервые использовался около 550 г. до н. э. с отправной точкой в ​​зимнее солнцестояние . [16]

Названия месяцев Хааб известны сегодня по их соответствующим названиям в колониальной эпохе юкатекских майя , как они были транскрибированы источниками 16-го века (в частности, Диего де Ландой и такими книгами, как Чилам Балам из Чумайеля). Фонематический анализ названий глифов Хааб в надписях доколумбовых майя показал, что названия для этих двадцатидневных периодов значительно различались от региона к региону и от периода к периоду, отражая различия в базовом языке(ах) и использовании в классическую и постклассическую эпохи, предшествовавшие их записи испанскими источниками. [17]

Каждый день в календаре Хаабʼ определялся номером дня в месяце, за которым следовало название месяца. Номера дней начинались с глифа, переводимого как «посадка» названного месяца, который обычно считается 0-м днем ​​этого месяца, хотя меньшинство считает его 20-м днем ​​месяца, предшествующего названному месяцу. В последнем случае посадка Попа приходится на 5-й день Вайебаʼ. Для большинства первым днем ​​года был 0 Поп (посадка Попа). За ним следовали 1 Поп, 2 Поп до 19 Поп, затем 0 Во, 1 Во и так далее.

Поскольку Хааб состоял из 365 дней, а тропический год составлял 365,2422 дня, дни Хааба не совпадали с тропическим годом.

Календарь Раунд

Дата Календарного Круга — это дата, которая дает и Цолькин, и Хааб. Эта дата повторится через 52 года Хааб или 18 980 дней, Календарный Круг. Например, текущее творение началось 4 Ахау 8 Кумку. Когда эта дата повторяется, это известно как завершение Календарного Круга.

Арифметически, продолжительность Календарного раунда является наименьшим общим кратным 260 и 365; 18 980 составляет 73 × 260 дней цолкин и 52 × 365 дней хааб. [18]

Не все возможные комбинации Цолкин и Хааб могут иметь место. Для дней Цолкин Имикс, Кими, Чувен и Киб день Хааб может быть только 4, 9, 14 или 19; для Ик, Маник, Эб и Кабан день Хааб может быть только 0, 5, 10 или 15; для Акб'аль, Ламат, Б'ен и Эц'наб день Хааб может быть только 1, 6, 11 или 16; для Кан, Мулук, Икс и Кавак день Хааб может быть только 2, 7, 12 или 17; и для Чикчан, Ок, Мен и Аджав день Хааб может быть только 3, 8, 13 или 18. [19]

Носитель года

«Носитель года» — это название дня Цолкин , которое приходится на 0  Pop, первый день Хааб . Поскольку существует 20 названий дней Цолкин, 365 дней в Хааб, и остаток от 365, деленный на 20, равен 5 ( 365 = 18×20 + 5 ), название дня Цолкин для каждого последующего 0  Pop будет на 5 позже в цикле названий дней Цолкин. Аналогично, поскольку существует 13 номеров дней Цолкин, и остаток от 365, деленный на 13, равен 1 ( 365 = 28×13 + 1 ), номер дня Цолкин для каждого последующего 0  Pop будет на 1 больше, чем раньше. Таким образом, последовательность дат Цолкин, соответствующих дате Хааб 0  Pop, выглядит следующим образом:

  • 1 Ик
  • 2 Маник
  • 3 Ebʼ
  • 4 Кабан
  • 5 Ик
  • ...
  • 12 Каб'ан
  • 13 Ик'
  • 1 Маник
  • ...

Таким образом, Хранители Года — это четыре названия дней Цолькина, которые появляются в этой последовательности: Ик, Маник, Эб и Кабан.

«Носитель года» буквально переводится как майянская концепция. [20] Его важность заключается в двух фактах. Во-первых, четыре года, возглавляемые Носителями года, названы в их честь и разделяют их характеристики; поэтому у них также есть свои собственные предсказания и божества-покровители. [21] Более того, поскольку Носители года географически идентифицируются с пограничными знаками или горами, они помогают определить местное сообщество. [22]

Классическая система Носителей Года, описанная выше, встречается в Тикале и в Дрезденском кодексе . В позднеклассический период в Кампече использовался другой набор Носителей Года. В этой системе Носителями Года были дни , совпадающие с 1 Pop. Это были Акб'аль, Ламат, Б'ен и Эзнаб. В постклассический период в Юкатане использовалась третья система. В этой системе Носителями Года были дни, совпадающие со 2 Pop: К'ан, Мулук, Икс и Кавак. Эта система встречается в Хронике Ошкуцкаба. Кроме того, как раз перед испанским завоеванием в Майяпане майя начали нумеровать дни Хааб' от 1 до 20. В этой системе Носители Года такие же, как и в системе 1 Pop – Кампече. Классическая система летосчисления до сих пор используется в горных районах Гватемалы [23], а также в Веракрусе, Оахаке и Чьяпасе, Мексика. [24]

Длинный счет

Восточная сторона Стелы C, Киригуа с мифической датой сотворения мира 13 бактунов, 0 катунов, 0 тунов, 0 уиналов, 0 кинов, 4 ахау, 8 кумуку – 11 августа 3114 г. до н.э. по пролептическому григорианскому календарю.

Поскольку даты Календарного Круга повторяются каждые 18 980 дней, примерно 52 солнечных года, цикл повторяется примерно один раз за всю жизнь, поэтому для точной записи истории требовался более совершенный метод датирования. Для указания дат за периоды, превышающие 52 года, жители Мезоамерики использовали календарь Длинного Счета.

Майя называли день kʼin . Двадцать таких kʼins известны как winal или uinal . Восемнадцать winal составляют один tun . Двадцать tun известны как kʼatun . Двадцать kʼatun составляют bʼakʼtun .

Календарь Длинного счета определяет дату, подсчитывая количество дней от даты сотворения мира майя 4 Ахав, 8 Кумку (11 августа 3114 г. до н. э. по пролептическому григорианскому календарю или 6 сентября по юлианскому календарю -3113 астрономического датирования). Но вместо использования десятичной ( десятичной ) схемы дни Длинного счета подсчитывались по модифицированной двадцатичной схеме. Таким образом, 0.0.0.1.5 равно 25, а 0.0.0.2.0 равно 40. Поскольку единица винал сбрасывается только после подсчета до 18, Длинный счет последовательно использует двадцатичную систему только в том случае, если основной единицей измерения считается тун, а не к'ин; при этом единицы к'ин и винал являются количеством дней в туне. Длинный счет 0.0.1.0.0 представляет 360 дней, а не 400 в чисто 20-ричной ( двадцатеричной ) системе исчисления.

Существуют также четыре редко используемых цикла высшего порядка: пиктун , калабтун , к'инчилтун и алаутун .

Поскольку даты Длинного счета недвусмысленны, Длинный счет был особенно хорошо приспособлен для использования на памятниках. Монументальные надписи включали не только 5 цифр Длинного счета, но также включали два символа цолкин, за которыми следовали два символа хааб.

Неправильная интерпретация месоамериканского календаря Длинного счета стала основой для популярного убеждения, что катаклизм произойдет 21 декабря 2012 года . 21 декабря 2012 года был просто днем, когда календарь перешел к следующему бактуну , в Длинном счете 13.0.0.0.0. Датой начала следующего бактуна (Длинный счет 14.0.0.0.0) является 26 марта 2407 года. Датой начала следующего пиктуна (полная серия из 20 бактунов), в Длинном счете 1.0.0.0.0.0, является 13 октября 4772 года.

Таблица единиц длинного счета

Единица длинного счета		Длинный
период счета		ДниПриблизительные
солнечные годы
1 К'ин 1 
1 Победа20 К'ин20 
1 тун18 Винал3601
1 Катун20 Тун7,20020
1 Бактун20 К'атун144,000394
1 Пиктун20 Бактун2,880,0007,885
1 Калабтун20 Пиктун57,600,000157,704
1 К'инчилтун20 Калабтун1,152,000,0003,154,071
1 Алаутун20 К'инчилтун23,040,000,00063,081,429

Дополнительная серия

Многие надписи классического периода включают серию глифов, известную как дополнительная серия. Принцип действия этой серии был в значительной степени разработан Джоном Э. Типлом . Дополнительная серия чаще всего состоит из следующих элементов:

Властелины ночи

Каждую ночь правил один из девяти владык подземного мира. Этот девятидневный цикл обычно записывался двумя глифами: глиф, который ссылался на Девять Владык как на группу, за которым следовал глиф для владыки, который будет править следующей ночью.

Лунная серия

Лунный ряд обычно записывается в виде пяти глифов, которые предоставляют информацию о текущей лунации , номере лунации в серии из шести, текущем правящем лунном божестве и продолжительности текущей лунации.

Возраст Луны

Майя считали количество дней в текущем лунном месяце. Они использовали две системы для нулевой даты лунного цикла: либо первая ночь, когда они могли видеть тонкий полумесяц, либо первое утро, когда они не могли видеть убывающую луну. [25] Возраст луны изображался набором глифов, которые майянисты называли глифами D и E:

  • Для обозначения нулевого дня лунного цикла использовался глиф новолуния.
  • Символы D использовались для обозначения лунного возраста с 1-го по 19-й день, а также количества дней, прошедших с момента новолуния.
  • Для лунных возрастов от 20 до 30 лет использовался глиф E с числом дней от 20.

Количество лунаций

Майя считали лунации. Этот цикл появляется в лунном ряду как два символа, которые современные ученые называют символами «C» и «X». Символ «C» мог иметь префикс в виде числа, указывающего на лунацию. Отсутствие префикса означало единицу, тогда как числа от двух до шести указывали на другие лунации. [26] [27] Также была часть символа «C», которая указывала, где это выпадало в большем цикле из 18 лунаций. Сопровождающий символ «C» был символом «X», который показывал похожую схему из 18 лунаций. [28] [29]

Длина лунации

Текущая эра лунного синодического периода составляет около 29.5305877 средних солнечных дней или около 29 дней 12 часов 44 минут и 2+ 7 / 9 секунд. Как целое число, количество дней в лунации будет либо 29, либо 30 дней, причем 30-дневные интервалы обязательно будут встречаться немного чаще, чем 29-дневные интервалы. Майя писали, был ли лунный месяц 29 или 30 дней, двумя глифами: глиф для длины лунации, за которым следовал либо глиф, состоящий из лунного глифа над связкой с суффиксом 9 для 29-дневной лунации, либо лунный глиф с суффиксом 10 для 30-дневной лунации. Поскольку майя не использовали дроби, лунации были приближены с помощью формулы, согласно которой 149 лунаций завершались за 4400 дней, что давало довольно короткий средний месяц, равный ровно 4400 / 149 = 29+ 79 / 149 дней = 29 дней 12 часов 43 минуты и 29+ 59 / 149 секунд, или около 29,5302 дня. [30]

819-дневный отсчет

Некоторые памятники майя включают глифы, которые фиксируют 819-дневный счет [31] в их начальной серии. Их также можно найти в Дрезденском кодексе . [32] Это описано у Томпсона. [33] Больше примеров этого можно найти у Келли. [34] Каждая группа из 819 дней была связана с одним из четырех цветов и основным направлением, с которым она была связана — черный соответствовал западу, красный — востоку, белый — северу, а желтый — югу.

Счет 819 дней можно описать несколькими способами: большинство из них упоминаются с помощью глифа «Y» и числа. Во многих также есть глиф для К'авилла — бога с дымящимся зеркалом в голове. Было высказано предположение, что К'авилл имеет связь с Юпитером. [35] В альманахе 59 Дрезденского кодекса есть чааки четырех цветов. Сопроводительные тексты начинаются с направляющего глифа и глагола для фраз счета 819 дней. Андерсон [36] дает подробное описание счета 819 дней.

Синодические периоды классических планет

 Луна: 1 x 819 + 8 дней = 28 (синодическое 29,53 дня) "28 месяцев" Луна: 4 x 819 + 2 дня = 111 (синодическое 29,53 дня) "111 месяцев" Луна: 15 x 819 + 0,3 дня = 416 (синодическое 29,53 дня) "416 месяцев"
 Драконический: 31 x 819 дней = 933 (драконический 27,21 дн.) «узловых месяца»
 Меркурий: 1 x 819 + 8 дней = 7 (синодический 115,88 дня) Меркурий: 15 x 819 + 2 дня = 106 (синодический 115,88 дня)
 Венера: 5 x 819 + 8 дней = 7 (синодический 583,9 дня)
 Солнце: 4 x 819 + 11 дней = 9 (синодическое 365,24 дня) "9 лет" Солнце: 33 x 819 + 1 день = 74 (синодическое 365,24 дня) "74 года"
 Марс: 20 x 819 + 2 дня = 21 (синодический 779,9 дня)
 Юпитер: 1 x 819 + 21 день = 2 (синодический 398,88 дня) Юпитер: 19 x 819 + 5 дней = 39 (синодический 398,88 дня)
 Сатурн: 6 x 819 - 1 день = 13 (синод 378,09 дня)

[37]

Короткий счет

В поздний классический период майя начали использовать сокращенный короткий счет вместо длинного счета. Пример этого можно найти на алтаре 14 в Тикале. [38] В королевствах постклассического Юкатана вместо длинного счета использовался короткий счет. Циклический короткий счет — это счет из 13 к'атунов (или 260 тунов), в котором каждый к'атун назывался в честь своего заключительного дня, Ахау («Господь»). 1 Имикс был выбран в качестве повторяющегося «первого дня» цикла, что соответствует 1 Чипактли в ацтекском счете дней. Цикл отсчитывался от катуна 11 Ахау до катуна 13 Ахау. Так как катун имеет длину 20 × 360 = 7200 дней, а остаток от 7200, деленный на 13, равен 11 ( 7200 = 553 × 13 + 11 ), то номер дня завершения каждого последующего катуна на 9 больше, чем раньше (переходя на 13, поскольку используются только 13 номеров дней). То есть, начиная с катуна, который начинается с 1  Imix, последовательность номеров дней завершения такова: 11, 9, 7, 5, 3, 1, 12, 10, 8, 6, 4, 2, 13, 11, ..., все они называются Ahau. За заключительным днем ​​13 Ahau следовал повторно входящий первый день 1 Imix. Это система, найденная в колониальных Книгах Чилам Балам . В характерной мезоамериканской манере эти книги проецируют цикл на ландшафт, где 13 «владений» Ахауобов делят землю Юкатана на 13 «королевств». [39]

Смотрите также

Примечания

  1. ^ Тедлок, Барбара, Время и горные майя, пересмотренное издание (1992 г., стр. 1) «Множество коренных общин Гватемалы, в основном говорящие на языках майя, известных как иксил, мам, покомчи и киче, придерживаются 260-дневного цикла, а во многих случаях и древнего солнечного цикла (глава 4)».
  2. ↑ Майлз, Сусанна В., «Анализ современных среднеамериканских календарей: исследование сохранения». В книге «Аккультурация в Америке». Под редакцией Сола Такса, стр. 273. Чикаго: Издательство Чикагского университета, 1952.
  3. ^ «Происхождение календаря майя: памятники, мифология и материализация времени».
  4. ↑ См. статью об Ицамне в книге Миллера и Таубе (1993), стр. 99–100.
  5. ^ ab Academia de las Lenguas Mayas de Guatemala (1988). Lenguas Mayas de Guatemala: Справочный документ по произношению новых официальных алфавитов . Город Гватемала: Национальный институт коренных народов.Подробную информацию и заметки об усыновлении в сообществе майянистов см. в работе Кеттунен и Хельмке (2020), стр. 7.
  6. ^ Тедлок (1992), стр. 1
  7. ^ «Мифологический» в том смысле, что Длинный счет был впервые придуман где-то в середине или конце доклассического периода, намного позже этой даты; см., например, Miller and Taube (1993, стр. 50).
  8. ^ Восс (2006, стр. 138)
  9. ↑ См. отдельную краткую статью в Википедии «Повелители ночи».
  10. ^ Стюарт, Дэвид (2024-04-19). "Day Sign Notes: Men / Tz'ikin". Расшифровка майя . Получено 2024-05-01 .
  11. ^ Реконструкции классической эпохи приведены в работе Кеттунена и Хельмке (2020), стр. 56–57.
  12. ^ Эдмонсон, Манро С. (1988). Книга года СРЕДНЕАМЕРИКАНСКИЕ КАЛЕНДРИАЛЬНЫЕ СИСТЕМЫ . Солт-Лейк-Сити: Издательство Университета Юты. стр. 20. ISBN 0-87480-288-1.
  13. ^ Кеттунен и Хельмке (2020), стр. 58–59.
  14. ^ Эти названия взяты из описания календаря де Ландой и широко используются майянистами, но классические майя не использовали эти фактические названия для знаков дня. Оригинальные названия неизвестны. См. Coe, Michael D. ; Mark L Van Stone (2005). Reading the Maya Glyphs. London: Thames & Hudson. p. 43. ISBN 978-0-500-28553-4.
  15. ^ abcd Ко, Майкл Д .; Марк Л. Ван Стоун (2005). Чтение иероглифов майя. Лондон: Thames & Hudson. стр. 43. ISBN 978-0-500-28553-4.
  16. ^ Zero Pop на самом деле выпал на тот же день, что и солнцестояние 12/27/−575, 12/27/−574, 12/27/−573 и 12/26/−572 ( астрономическая нумерация лет , всемирное время ), если не учитывать тот факт, что регион майя находится примерно в часовом поясе UT−6. См. сезоны IMCCE. Архивировано 23 августа 2012 г. на Wayback Machine
  17. ↑ Бут (2002), стр. 111–114.
  18. ↑ Более подробную информацию см. в Thompson 1966: 123–124.
  19. ^ Кеттунен и Хельмке (2020), с. 51
  20. ^ Томпсон 1966: 124
  21. ↑ Для более подробного изучения Носителей Года см. Tedlock 1992: 89–90; 99–104 и Thompson 1966.
  22. ↑ См. Коу 1965.
  23. ^ Тедлок 1992: 92
  24. ↑ Майлз, Сусанна В., «Анализ современных среднеамериканских календарей: исследование сохранения». В книге «Аккультурация в Америке». Под редакцией Сола Такса, стр. 273–284. Чикаго: Издательство Чикагского университета, 1952.
  25. ^ Томпсон, Дж. Эрик С. Иероглифическое письмо майя, 1950 г., стр. 236
  26. ↑ Типл 1931:53
  27. ^ Томпсон Иероглифическое письмо майя 1950:240
  28. ↑ Линден 1996:343–356.
  29. ^ Шеле, Грубе, Фазен 1992
  30. ↑ Типл 1931:67
  31. ^ "Мистический 819-дневный календарь майя" [The Mayan mystic 819-day calendar]. Мексиканские маршруты. 2024-12-26 . Получено 27 дек 2024 .
  32. ^ Грофе, Майкл Джон 2007 Серия «Змея»: Прецессия в Дрезденском кодексе майя, стр. 55, стр. 206
  33. ↑ Иероглифическое письмо майя 1971 стр. 212–217
  34. ↑ Дешифровка письменности майя, Дэвид Келли, 1973, стр. 56–57.
  35. ^ Звездные боги майя Сьюзен Милбрат 1999, Издательство Техасского университета
  36. ^ "Ллойд Б. Андерсон. 819-дневный счет майя и глиф "Y": вероятная связь с Юпитером". Домашняя страница Traditional High Cultures. Архивировано из оригинала 6 мая 2015 г. Получено 30 марта 2015 г.
  37. ^ 2023, Джон Х. Линден, Виктория Р. Брикер, 819-дневный счет майя и планетарная астрономия https://doi.org/10.1017/S0956536122000323
  38. ^ Ко, Уильям Р. «ТИКАЛ: справочник по древним руинам майя». Музей Пенсильванского университета, Филадельфия, Пенсильвания, 1967 г., стр. 114.
  39. ↑ Ройс 1967: 132, 184–185

Ссылки

  • Авени, Энтони Ф. (2001). Skywatchers (первоначально опубликовано как: Skywatchers of Ancient Mexico [1980], исправленное и обновленное издание). Остин: University of Texas Press . ISBN 0-292-70504-2. OCLC  45195586.
  • Бут, Эрик (2002). Предварительный классический майя-английский/англо-классический майяский словарь иероглифических чтений (PDF) . Mesoweb . Получено 10.11.2006 .
  • Брикер, Виктория Р. (февраль 1982 г.). «Происхождение солнечного календаря майя». Current Anthropology . 23 (1). Чикаго, Иллинойс: Издательство Чикагского университета , спонсируемое Фондом антропологических исследований Веннера-Грена : 101– 103. doi : 10.1086/202782. ISSN  0011-3204. OCLC  62217742. S2CID  143962107.
  • Чемберс, Дэвид Уэйд (1965). «Знали ли майя цикл Метона». Isis . 56 (3): 348– 351. doi :10.1086/350004. S2CID  145711182.
  • Ко, Майкл Д. (1965). «Модель структуры древнего сообщества майя в низинах майя». Southwestern Journal of Anthropology . 21. doi :10.1086/soutjanth.21.2.3629386. S2CID  130245359.
  • Ко, Майкл Д. (1987). Майя (4-е исправленное издание). Лондон и Нью-Йорк: Thames & Hudson . ISBN 0-500-27455-X. OCLC  15895415.
  • Ко, Майкл Д. (1992). Взлом кода майя. Лондон: Thames & Hudson . ISBN 0-500-05061-9. OCLC  26605966.
  • Фостер, Линн В. (2002). Справочник по жизни в древнем мире майя . с предисловием Питера Мэтьюза. Нью-Йорк: Факты в деле . ISBN 0-8160-4148-2. OCLC  50676955.
  • Иванофф, Пьер (1971). Mayan Enigma: The Search for a Lost Civilization . Элейн П. Гальперин (перевод) (перевод Découvertes chez les Mayas , англ. ред.). Нью-Йорк: Delacorte Press. ISBN 0-440-05528-8. OCLC  150172.
  • Джонс, Кристофер (1984). Расшифровка иероглифов майя . Карл П. Битц (илл.) (подготовлено для семинара выходного дня 7 и 8 апреля 1984 г., 2-е изд.). Филадельфия: Музей университета, Университет Пенсильвании . OCLC  11641566.
  • Кеттунен, Харри; Кристоф Хельмке (2020). Введение в иероглифы майя: 17-е издание (PDF) . Кувен, Бельгия: Вайеб . Проверено 6 октября 2020 г.
  • Линден, Джон Х. (1996). Варианты головы божества символа C. The Eight Palenque Round Table, 1993. С.  343–356 .
  • MacDonald, G. Jeffrey (27 марта 2007 г.). «Предсказывает ли календарь майя апокалипсис 2012 года?». USA Today . McLean, VA: Gannett Company . ISSN  0734-7456. Архивировано из оригинала 2008-03-16 . Получено 2009-05-28 .
  • Милбрат, Сьюзен (1999). Звездные боги майя: астрономия в искусстве, фольклоре и календарях . Серия Линды Шейл в майя и доколумбовых исследованиях. Остин: University of Texas Press . ISBN 0-292-75225-3. OCLC  40848420.
  • Миллер, Мэри ; Карл Таубе (1993). Боги и символы Древней Мексики и майя: Иллюстрированный словарь мезоамериканской религии. Лондон: Темза и Гудзон. ISBN 0-500-05068-6. OCLC  27667317.
  • Райс, Пруденс М., Происхождение календаря майя: памятники, мифология и материализация времени (Остин, Техас: Издательство Техасского университета, 2007).
  • Робинсон, Эндрю (2000). История письма: алфавиты, иероглифы и пиктограммы . Лондон и Нью-Йорк: Темза и Гудзон . ISBN 0-500-28156-4. OCLC  59432784.
  • Ройс, Ральф Л. (1967). Книга Чилама Балама из Чумайеля . Норман: Издательство Университета Оклахомы .
  • Schele, Linda ; David Freidel (1992). Лес королей: нерассказанная история древних майя (первоначально опубликовано New York: Morrow, 1990, pbk reprint ed.). New York: Harper Perennial . ISBN 0-688-11204-8. OCLC  145324300.
  • Шеле, Линда; Николай Грубе; Федерико Фасен (октябрь 1992 г.). «Лунная серия в классических надписях майя: новые наблюдения и интерпретации». Техасские заметки о доколумбовом искусстве, письме и культуре (29).
  • Тауб, Бен (19.04.2023). «Мы наконец-то знаем, как календарь майя совпадает с планетами». IFLScience .
  • Тедлок, Барбара (1992). Время и горные майя (ред. ред.). Альбукерке: Издательство Университета Нью-Мексико . ISBN 0-8263-0577-6. OCLC  7653289.
  • Типл, Джон Э. (ноябрь 1931 г.). «Астрономия майя» (PDF) . Вклад в американскую археологию . Том I (издание 403-е изд.). Вашингтон, округ Колумбия: Институт Карнеги в Вашингтоне. С.  29–116 .
  • Тедлок, Деннис , ред. (1985). Пополь Вух: окончательное издание майянской книги о заре жизни и славе богов и королей . Перевод Тедлока, Денниса. с комментариями, основанными на древних знаниях современных майя киче. Нью-Йорк: Simon & Schuster . ISBN 0-671-45241-X. OCLC  11467786.
  • Thomas, Cyrus (1897). «Day Symbols of the Maya Year». В JW Powell (ed.). Sixteenth Annual Report of the Bureau of American Ethnology to the Secretary of the Smithsonian Institution, 1894–1895 (электронная онлайн-репродукция). Вашингтон, округ Колумбия: Bureau of American Ethnology , Smithsonian Institution ; US Government Printing Office . стр.  199–266 . OCLC  14963920. Архивировано из оригинала 22 января 2007 г. – через Project Gutenberg .
  • Томпсон, Дж. Эрик С. (1971). Иероглифическое письмо майя: Введение, 3-е издание . Серия «Цивилизация американских индейцев», № 56 (3-е изд.). Норман: Издательство Университета Оклахомы . ISBN 0-8061-0447-3. OCLC  275252.
  • Тоззер, Альфред М. , изд. (1941). Relación de las cosas de Yucatán Ланды: перевод . Документы Музея американской археологии и этнологии Пибоди, Гарвардский университет, том. 18. Перевод Тоззера, Альфреда М. Чарльза П. Боудича и Ральфа Л. Рояса (дополнительный перевод) (перевод Relación de las cosas de Yucatán Диего де Ланды [оригинал около 1566 г.], с примечаниями, комментариями и приложения, включающие переведенные отрывки из произведений Гаспара Антонио Чи , Томаса Лопеса Меделя, Франциско Сервантес де Саласар и Антонио де Эррера-и-Тордесильяс , английское изд.). Кембридж, Массачусетс: Музей археологии и этнологии Пибоди . OCLC  625693.
  • Восс, Александр (2006). «Астрономия и математика». В Николае Грубе (ред.). Майя: Божественные короли дождевого леса . Ева Эггебрехт и Маттиас Зайдель (помощники редакторов). Кельн, Германия: Könemann. стр.  130–143 . ISBN 978-3-8331-1957-6. OCLC  71165439.
На Викискладе есть медиафайлы по теме «Календарь майя».
  • Символы дня года майя в проекте Гутенберг 1897 текст Сайруса Томаса
  • Конвертер дат в FAMSI Этот конвертер использует юлианский/григорианский календарь и включает 819-дневный цикл и лунный возраст.
  • Интерактивные календари майя


Взято с "https://en.wikipedia.org/w/index.php?title=Maya_calendar&oldid=1265667639"