Продукт (математика)

Арифметические операции в т е

Дополнение (+) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{term}}\,+\,{\text{term}}\\\scriptstyle {\text{summand}}\,+\,{\text{summand}}\\\scriptstyle {\text{addend}}\,+\,{\text{addend}}\\\scriptstyle {\text{augend}}\,+\,{\text{addend}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{сумма}}}$ Вычитание (−) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{term}}\,-\,{\text{term}}\\\scriptstyle {\text{minuend}}\,-\,{\text{subtrahend}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{разница}}}$ Умножение (×) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{factor}}\,\times \,{\text{factor}}\\\scriptstyle {\text{multiplier}}\,\times \,{\text{multiplicand}}\end{matrix}}\right\}\,=\,}$ product {\displaystyle \scriptstyle {\text{product}}} Division (÷) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{dividend}}}{\scriptstyle {\text{divisor}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{numerator}}}{\scriptstyle {\text{denominator}}}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle \left\{{\begin{matrix}\scriptstyle {\text{fraction}}\\\scriptstyle {\text{quotient}}\\\scriptstyle {\text{ratio}}\end{matrix}}\right.}$ Exponentiation (^) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{base}}^{\text{exponent}}\\\scriptstyle {\text{base}}^{\text{power}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{power}}}$ nth root (√) ${\displaystyle \scriptstyle {\sqrt[{\text{degree}}]{\scriptstyle {\text{radicand}}}}\,=\,}$ ${\displaystyle \scriptstyle {\text{root}}}$ Logarithm (log) ${\displaystyle \scriptstyle \log _{\text{base}}({\text{anti-logarithm}})\,=\,}$ ${\displaystyle \scriptstyle {\text{logarithm}}}$

v t e

В математике произведение — это результат умножения или выражение , которое определяет объекты (числа или переменные ), которые нужно умножить, называемые множителями . Например, 21 — это произведение 3 и 7 (результат умножения), а также является произведением и (указывающим на то, что два множителя следует умножить друг на друга). Когда один множитель — целое число , произведение называется кратным .${\displaystyle x\cdot (2+x)}$${\displaystyle x}$${\displaystyle (2+x)}$

Порядок, в котором умножаются действительные или комплексные числа, не влияет на результат; это известно как коммутативный закон умножения. Когда умножаются матрицы или члены различных других ассоциативных алгебр , результат обычно зависит от порядка множителей. Например, умножение матриц некоммутативно, как и умножение в других алгебрах в целом.

В математике существует множество различных видов произведений: помимо возможности умножать только числа, многочлены или матрицы, можно также определять произведения на многих различных алгебраических структурах .

Первоначально произведение было и остается результатом умножения двух или более чисел . Например, 15 является произведением 3 и 5. Основная теорема арифметики гласит, что каждое составное число является произведением простых чисел , которое уникально с точностью до порядка множителей.

С введением математической нотации и переменных в конце 15-го века стало обычным рассматривать умножение чисел, которые либо не указаны ( коэффициенты и параметры ), либо должны быть найдены ( неизвестные ). Эти умножения, которые не могут быть эффективно выполнены, называются произведениями . Например, в линейном уравнении термин обозначает произведение коэффициента и неизвестного${\displaystyle ax+b=0,}$${\displaystyle ax}$${\displaystyle a}$${\displaystyle x.}$

Позже, и по сути с 19-го века, были введены новые бинарные операции , которые вообще не связаны с числами и были названы произведениями ; например, скалярное произведение . Большая часть этой статьи посвящена таким нечисловым произведениям.

Оператор произведения для произведения последовательности обозначается заглавной греческой буквой пи Π (по аналогии с использованием заглавной сигмы Σ в качестве символа суммирования ). ^[1] Например, выражение представляет собой другой способ записи ⁠ ⁠ . ^[2]${\displaystyle \textstyle \prod _{i=1}^{6}i^{2}}$${\displaystyle 1\cdot 4\cdot 9\cdot 16\cdot 25\cdot 36}$

Произведение последовательности, состоящей только из одного числа, представляет собой само это число; произведение без каких-либо множителей называется пустым произведением и равно 1.

Коммутативные кольца имеют операцию произведения.

Остаточные классы в кольцах могут быть добавлены:${\displaystyle \mathbb {Z} /N\mathbb {Z} }$

${\displaystyle (a+N\mathbb {Z} )+(b+N\mathbb {Z} )=a+b+N\mathbb {Z} }$

и умножается:

${\displaystyle (a+N\mathbb {Z} )\cdot (b+N\mathbb {Z} )=a\cdot b+N\mathbb {Z} }$

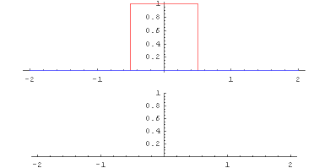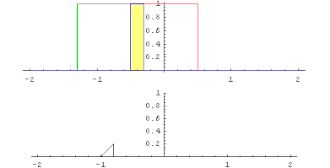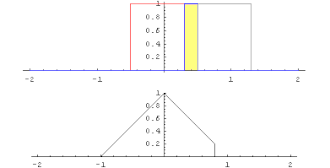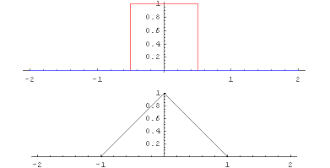
Две функции от действительных чисел к самим себе можно умножить другим способом, называемым сверткой .

Если

${\displaystyle \int \limits _{-\infty }^{\infty }|f(t)|\,\mathrm {d} t<\infty \qquad {\mbox{and}}\qquad \int \limits _{-\infty }^{\infty }|g(t)|\,\mathrm {d} t<\infty ,}$

тогда интеграл

${\displaystyle (f*g)(t)\;:=\int \limits _{-\infty }^{\infty }f(\tau )\cdot g(t-\tau )\,\mathrm {d} \tau }$

хорошо определена и называется сверткой.

При преобразовании Фурье свертка превращается в поточечное умножение функций.

Произведение двух многочленов определяется следующим образом:

${\displaystyle \left(\sum _{i=0}^{n}a_{i}X^{i}\right)\cdot \left(\sum _{j=0}^{m}b_{j}X^{j}\right)=\sum _{k=0}^{n+m}c_{k}X^{k}}$

с

${\displaystyle c_{k}=\sum _{i+j=k}a_{i}\cdot b_{j}}$

В линейной алгебре существует множество различных видов произведений. Некоторые из них имеют схожие названия ( внешнее произведение , внешнее произведение ) с очень разными значениями, в то время как другие имеют очень разные названия (внешнее произведение, тензорное произведение, произведение Кронекера), но при этом передают по сути одну и ту же идею. Их краткий обзор дан в следующих разделах.

По определению векторного пространства можно образовать произведение любого скаляра на любой вектор, получив отображение .${\displaystyle \mathbb {R} \times V\rightarrow V}$

Скалярное произведение — это билинейное отображение:

${\displaystyle \cdot :V\times V\rightarrow \mathbb {R} }$

при следующих условиях, что для всех .${\displaystyle v\cdot v>0}$${\displaystyle 0\not =v\in V}$

Из скалярного произведения можно определить норму , положив .${\displaystyle \|v\|:={\sqrt {v\cdot v}}}$

Скалярное произведение также позволяет определить угол между двумя векторами:

${\displaystyle \cos \angle (v,w)={\frac {v\cdot w}{\|v\|\cdot \|w\|}}}$

В -мерном евклидовом пространстве стандартное скалярное произведение (называемое скалярным произведением ) определяется по формуле:${\displaystyle n}$

${\displaystyle \left(\sum _{i=1}^{n}\alpha _{i}e_{i}\right)\cdot \left(\sum _{i=1}^{n}\beta _{i}e_{i}\right)=\sum _{i=1}^{n}\alpha _{i}\,\beta _{i}}$

Перекрестное произведение двух векторов в трехмерном пространстве — это вектор, перпендикулярный двум сомножителям, длина которого равна площади параллелограмма, образованного этими двумя сомножителями.

Перекрестное произведение также можно выразить как формальный определитель ^[a] :

${\displaystyle \mathbf {u\times v} ={\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\u_{1}&u_{2}&u_{3}\\v_{1}&v_{2}&v_{3}\\\end{vmatrix}}}$

Линейное отображение можно определить как функцию f между двумя векторными пространствами V и W с базовым полем F , удовлетворяющую ^[3]

${\displaystyle f(t_{1}x_{1}+t_{2}x_{2})=t_{1}f(x_{1})+t_{2}f(x_{2}),\forall x_{1},x_{2}\in V,\forall t_{1},t_{2}\in \mathbb {F} .}$

Если рассматривать только конечномерные векторные пространства, то

${\displaystyle f(\mathbf {v} )=f\left(v_{i}\mathbf {b_{V}} ^{i}\right)=v_{i}f\left(\mathbf {b_{V}} ^{i}\right)={f^{i}}_{j}v_{i}\mathbf {b_{W}} ^{j},}$

где b _V и b _W обозначают основания V и W , а ^v i _{обозначает} компонент v по b V i _, и применяется соглашение Эйнштейна о суммировании .

Теперь рассмотрим композицию двух линейных отображений между конечномерными векторными пространствами. Пусть линейное отображение f отображает V в W , а линейное отображение g отображает W в U . Тогда можно получить

${\displaystyle g\circ f(\mathbf {v} )=g\left({f^{i}}_{j}v_{i}\mathbf {b_{W}} ^{j}\right)={g^{j}}_{k}{f^{i}}_{j}v_{i}\mathbf {b_{U}} ^{k}.}$

Или в матричной форме:

${\displaystyle g\circ f(\mathbf {v} )=\mathbf {G} \mathbf {F} \mathbf {v} ,}$

в котором элемент i-й строки, j -го столбца матрицы F , обозначенный F _ij , равен f ^j _i , а G _ij =g ^j _i .

Композицию более чем двух линейных отображений можно аналогично представить цепочкой умножения матриц.

Даны две матрицы

${\displaystyle A=(a_{i,j})_{i=1\ldots s;j=1\ldots r}\in \mathbb {R} ^{s\times r}}$и${\displaystyle B=(b_{j,k})_{j=1\ldots r;k=1\ldots t}\in \mathbb {R} ^{r\times t}}$

их произведение дается выражением

${\displaystyle B\cdot A=\left(\sum _{j=1}^{r}a_{i,j}\cdot b_{j,k}\right)_{i=1\ldots s;k=1\ldots t}\;\in \mathbb {R} ^{s\times t}}$

Существует связь между композицией линейных функций и произведением двух матриц. Чтобы увидеть это, пусть r = dim(U), s = dim(V) и t = dim(W) будут (конечными) размерностями векторных пространств U, V и W. Пусть будет базисом U, будет базисом V и будет базисом W. В терминах этого базиса пусть будет матрицей, представляющей f : U → V, а будет матрицей, представляющей g : V → W. Тогда${\displaystyle {\mathcal {U}}=\{u_{1},\ldots ,u_{r}\}}$${\displaystyle {\mathcal {V}}=\{v_{1},\ldots ,v_{s}\}}$${\displaystyle {\mathcal {W}}=\{w_{1},\ldots ,w_{t}\}}$${\displaystyle A=M_{\mathcal {V}}^{\mathcal {U}}(f)\in \mathbb {R} ^{s\times r}}$${\displaystyle B=M_{\mathcal {W}}^{\mathcal {V}}(g)\in \mathbb {R} ^{r\times t}}$

${\displaystyle B\cdot A=M_{\mathcal {W}}^{\mathcal {U}}(g\circ f)\in \mathbb {R} ^{s\times t}}$

представляет собой матрицу .${\displaystyle g\circ f:U\rightarrow W}$

Другими словами: матричное произведение — это описание в координатах композиции линейных функций.

Для двух конечномерных векторных пространств V и W их тензорное произведение можно определить как (2,0)-тензор, удовлетворяющий:

${\displaystyle V\otimes W(v,m)=V(v)W(w),\forall v\in V^{*},\forall w\in W^{*},}$

где V ^* и W ^* обозначают двойственные пространства V и W . ^[4 ]

Для бесконечномерных векторных пространств также имеет место:

• Тензорное произведение гильбертовых пространств
• Топологическое тензорное произведение .

Тензорное произведение, внешнее произведение и произведение Кронекера передают одну и ту же общую идею. Различия между ними в том, что произведение Кронекера — это просто тензорное произведение матриц относительно заранее фиксированного базиса, тогда как тензорное произведение обычно дается в его внутреннем определении . Внешнее произведение — это просто произведение Кронекера, ограниченное векторами (вместо матриц).

В общем, когда есть два математических объекта , которые можно объединить таким образом, чтобы они вели себя как тензорное произведение линейной алгебры, то это можно наиболее обще понимать как внутреннее произведение моноидальной категории . То есть моноидальная категория точно передает смысл тензорного произведения; она точно передает идею того, почему тензорные произведения ведут себя именно так, а не иначе. Точнее, моноидальная категория — это класс всех вещей (заданного типа ), которые имеют тензорное произведение.

Другие виды произведений в линейной алгебре включают в себя:

• продукт Адамара
• продукт Кронекера
• Произведение тензоров :
  • Клиновое изделие или наружное изделие
  • Изделия для интерьера
  • Внешний продукт
  • Тензорное произведение

В теории множеств декартово произведение — это математическая операция , которая возвращает множество (или множество произведений ) из нескольких множеств. То есть, для множеств A и B декартово произведение A × B — это множество всех упорядоченных пар (a, b) —где a ∈ A и b ∈ B. ^[5]

Класс всех вещей (данного типа ), которые имеют декартовы произведения, называется декартовой категорией . Многие из них являются декартовыми замкнутыми категориями . Множества являются примером таких объектов.

Пустое произведение чисел и большинства алгебраических структур имеет значение 1 (элемент тождества умножения), точно так же, как пустая сумма имеет значение 0 (элемент тождества сложения). Однако концепция пустого произведения является более общей и требует специального рассмотрения в логике , теории множеств , компьютерном программировании и теории категорий .

Произведения над другими видами алгебраических структур включают:

• декартово произведение множеств
• прямое произведение групп , а также полупрямое произведение , вязаное произведение и сплетенное произведение
• свободный продукт групп
• произведение колец
• продукт идеалов
• произведение топологических пространств ^[1]
• произведение Вика случайных величин
• шапочка , чашка , Мэсси и наклонное произведение в алгебраической топологии
• произведение разбиения и сумма клина (иногда называемая произведением клина) в гомотопии

Некоторые из приведенных выше произведений являются примерами общего понятия внутреннего произведения в моноидальной категории ; остальные описываются общим понятием произведения в теории категорий .

Все предыдущие примеры являются частными случаями или примерами общего понятия продукта. Для общей трактовки понятия продукта см. продукт (теория категорий) , который описывает, как объединить два объекта некоторого вида, чтобы создать объект, возможно, другого вида. Но также в теории категорий есть:

• волокнистый продукт или обратный поток,
• категория продукта , категория, которая является продуктом категорий.
• ультрапродукт в теории моделей .
• внутреннее произведение моноидальной категории , которое отражает суть тензорного произведения.

• Интеграл произведения функции (как непрерывный эквивалент произведения последовательности или как мультипликативная версия нормального/стандартного/аддитивного интеграла). Интеграл произведения также известен как «непрерывное произведение» или «мультипликативный».
• Комплексное умножение , теория эллиптических кривых.

• Тензорное произведение Делиня абелевых категорий  – бельгийский математикPages displaying short descriptions of redirect targets
• Неопределенный продукт
• Бесконечное произведение
• Повторяющаяся бинарная операция  – повторное применение операции к последовательности.
• Умножение  – арифметическая операция

• Ярхов, Ганс (1981). Локально выпуклые пространства . Штутгарт: Б. Г. Тойбнер. ISBN 978-3-519-02224-4. OCLC  8210342.