Соединение (векторный пучок)
В математике , и особенно в дифференциальной геометрии и калибровочной теории , связность на расслоении волокон — это устройство, которое определяет понятие параллельного переноса на расслоении; то есть способ «соединить» или идентифицировать волокна над близлежащими точками. Наиболее распространенным случаем является линейная связность на векторном расслоении , для которой понятие параллельного переноса должно быть линейным . Линейная связность эквивалентно задается ковариантной производной , оператором, который дифференцирует сечения расслоения вдоль касательных направлений в базовом многообразии таким образом, что параллельные сечения имеют нулевую производную. Линейные связности обобщают на произвольные векторные расслоения связность Леви-Чивиты на касательном расслоении псевдориманова многообразия , что дает стандартный способ дифференцировать векторные поля. Нелинейные связности обобщают эту концепцию на расслоения, волокна которых не обязательно линейны.
Линейные связи также называются связями Кошуля в честь Жана-Луи Кошуля , который дал алгебраическую основу для их описания (Koszul 1950).
В этой статье определяется связь на векторном расслоении с использованием общей математической нотации, которая де-акцентирует внимание на координатах. Однако, другие нотации также регулярно используются: в общей теории относительности вычисления векторных расслоений обычно записываются с использованием индексированных тензоров; в калибровочной теории подчеркиваются эндоморфизмы волокон векторного пространства. Различные нотации эквивалентны, как обсуждалось в статье о метрических связях (комментарии, сделанные там, применимы ко всем векторным расслоениям).
Мотивация
Пусть M — дифференцируемое многообразие , например, евклидово пространство . Векторнозначную функцию можно рассматривать как сечение тривиального векторного расслоения. Можно рассмотреть сечение общего дифференцируемого векторного расслоения, и поэтому естественно задаться вопросом , можно ли дифференцировать сечение, как обобщение того, как дифференцируется функция на M.
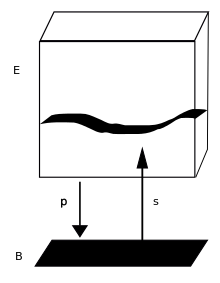
Модельный случай — дифференцировать функцию на евклидовом пространстве . В этой постановке производная в точке направления может быть определена стандартной формулой
Для каждого это определяет новый вектор
При переходе к секции векторного расслоения над многообразием мы сталкиваемся с двумя ключевыми проблемами этого определения. Во-первых, поскольку многообразие не имеет линейной структуры, термин не имеет смысла на . Вместо этого мы берем путь такой, что и вычисляем
Однако это все еще не имеет смысла, поскольку и являются элементами различных векторных пространств и Это означает, что вычитание этих двух членов не определено естественным образом.
Проблема решается введением дополнительной структуры связи в векторное расслоение. Существует по крайней мере три перспективы, из которых связи могут быть поняты. При точной формулировке все три перспективы эквивалентны.
- ( Параллельный перенос ) Соединение можно рассматривать как назначение каждому дифференцируемому пути линейного изоморфизма для всех Используя этот изоморфизм можно перенести в волокно и затем взять разность; явно, Для того чтобы это зависело только от и не от расширяющегося пути , необходимо наложить ограничения (в определении) на зависимость от Это не так просто сформулировать, и поэтому это понятие «параллельного переноса» обычно выводится как побочный продукт других способов определения соединений. Фактически, следующее понятие «связь Эресмана» есть не что иное, как инфинитезимальная формулировка параллельного переноса.
- ( Связность Эресмана ) Сечение можно рассматривать как гладкое отображение из гладкого многообразия в гладкое многообразие Таким образом, можно рассмотреть прямой образ , который является элементом касательного пространства В формулировке связности Эресмана выбирается способ назначения каждому и каждому разложения прямой суммы на два линейных подпространства, одно из которых является естественным вложением С этими дополнительными данными определяется путем проецирования , которое может быть оценено в Для того чтобы соблюдать линейную структуру векторного расслоения, накладываются дополнительные ограничения на то, как разложение прямой суммы движется при изменении e по слою.
- ( Ковариантная производная ) Стандартная производная в евклидовых контекстах удовлетворяет определенным зависимостям от и наиболее фундаментальной из них является линейность. Ковариантная производная определяется как любая операция , которая имитирует эти свойства вместе с формой правила произведения .
Если только база не нульмерна, всегда существует бесконечно много связей, которые существуют на данном дифференцируемом векторном расслоении, и поэтому всегда существует соответствующий выбор того, как дифференцировать сечения. В зависимости от контекста могут быть выделенные выборы, например, те, которые определяются путем решения определенных уравнений в частных производных . В случае касательного расслоения любая псевдориманова метрика (и в частности любая риманова метрика ) определяет каноническую связь, называемую связью Леви-Чивиты .
Формальное определение
Пусть — гладкое вещественное векторное расслоение над гладким многообразием . Обозначим пространство гладких сечений через . Ковариантная производная по — это одна из следующих эквивалентных структур:
- - линейное отображение , такое что правило произведения выполняется для всех гладких функций на и всех гладких сечений
- присвоение любому гладкому сечению s и каждому -линейного отображения , которое гладко зависит от x и такое, что для любых двух гладких сечений и любых действительных чисел и такое, что для каждой гладкой функции , связано с для любого и
За исключением использования канонического отождествления между векторным пространством и векторным пространством линейных отображений эти два определения идентичны и отличаются только используемым языком.
Обычно обозначают с неявным присутствием в При такой записи правило произведения во второй версии определения, данного выше, записывается
Замечание. В случае комплексного векторного расслоения приведенное выше определение все еще имеет смысл, но обычно его модифицируют, меняя "действительный" и " " везде, где они появляются, на "комплексный" и " " Это накладывает дополнительные ограничения, поскольку не каждое действительно-линейное отображение между комплексными векторными пространствами является комплексно-линейным. В этом различии есть некоторая двусмысленность, поскольку комплексное векторное расслоение можно также рассматривать как действительное векторное расслоение.
Индуцированные связи
Если дано векторное расслоение , то существует множество ассоциированных расслоений, к которым можно построить, например, дуальное векторное расслоение , тензорные степени , симметричные и антисимметричные тензорные степени и прямые суммы . Связь на индуцирует связь на любом из этих ассоциированных расслоений. Легкость перехода между связями на ассоциированных расслоениях более элегантно отражается теорией главных связей расслоений , но здесь мы представляем некоторые из основных индуцированных связей.
Двойное соединение
При наличии связи на индуцированная двойственная связь на определяется неявно как
Здесь — гладкое векторное поле, — сечение , а — сечение двойственного расслоения, и естественное спаривание между векторным пространством и его двойственным (происходящее на каждом волокне между и ), то есть . Обратите внимание, что это определение по сути обеспечивает, чтобы было соединение на , так что для спаривания выполняется правило естественного произведения .
Соединение тензорного продукта
Для заданных связностей на двух векторных расслоениях определите связность тензорного произведения по формуле
Здесь мы имеем . Обратите внимание, что это естественный способ объединения для обеспечения правила продукта для связности тензорного продукта. Повторным применением приведенной выше конструкции к тензорному продукту , также получаем связность тензорной мощности для любого и векторного расслоения .
Прямая сумма соединения
Прямая сумма связи определяется как
где .
Симметричные и внешние силовые соединения
Поскольку симметричная мощность и внешняя мощность векторного расслоения могут рассматриваться естественным образом как подпространства тензорной мощности, определение связности тензорного произведения применяется к этой настройке напрямую. Действительно, поскольку симметричная и внешняя алгебры находятся внутри тензорной алгебры как прямые слагаемые, а связь соблюдает это естественное расщепление, можно просто ограничиться этими слагаемыми. Явно, определить связность симметричного произведения следующим образом:
и внешнее соединение продукта
для всех . Повторное применение этих продуктов дает индуцированную симметричную мощность и внешние силовые соединения на и соответственно.
Эндоморфизм связи
Наконец, можно определить индуцированную связность на векторном расслоении эндоморфизмов , связность эндоморфизмов . Это просто связность тензорного произведения двойственной связности на и на . Если и , так что композиция также, то для связности эндоморфизмов выполняется следующее правило произведения:
Обратив это уравнение, можно определить эндоморфную связь как единственную связь, удовлетворяющую
для любого , что позволяет избежать необходимости сначала определять двойственную связность и связность тензорного произведения.
Любой связанный пакет
Если задано векторное расслоение ранга и любое представление в линейную группу , то существует индуцированная связь на ассоциированном векторном расслоении . Эта теория наиболее кратко излагается путем перехода к связи главного расслоения на расслоении фрейма и использования теории главных расслоений. Каждый из приведенных выше примеров можно рассматривать как частные случаи этой конструкции: двойственное расслоение соответствует обратному транспонированному (или обратному сопряженному) представлению, тензорное произведение — представлению тензорного произведения, прямая сумма — представлению прямой суммы и т. д.
Внешняя ковариантная производная и векторные формы
Пусть — векторное расслоение. -значная дифференциальная форма степени — это сечение расслоения тензорного произведения :
Пространство таких форм обозначается
где последнее тензорное произведение обозначает тензорное произведение модулей над кольцом гладких функций на .
-значная 0-форма — это всего лишь часть пакета . То есть,
В этой нотации связь на является линейным отображением
Тогда связь можно рассматривать как обобщение внешней производной на формы со значениями векторного расслоения. Фактически, если задана связь на , то существует единственный способ расширить ее до внешней ковариантной производной
Эта внешняя ковариантная производная определяется следующим правилом Лейбница, которое задано на простых тензорах вида и расширено линейно:
где так что , является разделом, и обозначает -форму со значениями в , определяемыми путем вклинивания с частью формы с одной формой . Обратите внимание, что для -значных 0-форм это восстанавливает нормальное правило Лейбница для соединения .
В отличие от обычной внешней производной, обычно имеет . Фактически, напрямую связана с кривизной соединения (см. ниже).
Аффинные свойства множества связей
Каждое векторное расслоение над многообразием допускает связь, что можно доказать с помощью разбиений единицы . Однако связи не являются уникальными. Если и являются двумя связями на , то их разность является -линейным оператором. То есть,
для всех гладких функций на и всех гладких сечений . Отсюда следует, что разность может быть однозначно идентифицирована с одной формой на со значениями в расслоении эндоморфизмов :
Наоборот, если есть соединение на и есть одноформа на со значениями в , то есть соединение на .
Другими словами, пространство связей на является аффинным пространством для . Это аффинное пространство обычно обозначается .
Отношение к принципалу и соединениям Эресмана
Пусть будет векторным расслоением ранга и пусть будет расслоением фрейма . Тогда (главная) связность на индуцирует связность на . Сначала отметим, что сечения находятся во взаимно однозначном соответствии с правыми эквивариантными отображениями . (Это можно увидеть, рассмотрев обратный образ над , который изоморфен тривиальному расслоению .) Для данного сечения пусть соответствующее эквивариантное отображение будет . Ковариантная производная на тогда задается как
где горизонтальная подъемная сила от до . (Напомним, что горизонтальная подъемная сила определяется связью с . )
И наоборот, связь на определяет связь на , и эти две конструкции являются взаимно обратными.
Связность на также эквивалентно определяется линейной связностью Эресмана на . Это обеспечивает один из методов построения соответствующей главной связи.
Индуцированные связи, обсуждаемые в #Индуцированные связи, могут быть построены как связи на других ассоциированных расслоениях с расслоением фрейма , используя представления , отличные от стандартного представления, использованного выше. Например, если обозначает стандартное представление на , то ассоциированное расслоение с представлением на является расслоением прямой суммы , а индуцированная связь — это именно то, что было описано выше.
Местное выражение
Пусть будет векторным расслоением ранга , и пусть будет открытым подмножеством над которым тривиализируется. Поэтому над множеством , допускает локальный гладкий фрейм сечений
Поскольку рамка определяет базис волокна для любого , можно разложить любой локальный участок в рамке как
для набора гладких функций .
При наличии связи на можно выразить через локальную систему сечений, используя правило характеристического произведения для связи. Для любой базовой секции величина может быть расширена в локальной системе сечений как
где — набор локальных однократных форм. Эти формы можно поместить в матрицу однократных форм, определяемую
называется локальной формой связи над . Действие на любой секции может быть вычислено с использованием правила произведения как
Если локальный раздел также записан в матричной записи как вектор-столбец, используя локальный фрейм в качестве основы,
то, используя обычное умножение матриц, можно записать
где — это сокращение для применения внешней производной к каждому компоненту как вектор-столбец. В этой нотации часто локально пишут, что . В этом смысле связь локально полностью определяется ее формой связи в некоторой тривиализации.
Как объясняется в #Аффинные свойства множества связей, любая связь отличается от другой эндоморфно-значной одноформой. С этой точки зрения одноформа связи — это именно эндоморфно-значная одноформа, такая, что связь на отличается от тривиальной связи на , которая существует, поскольку является тривиализующим множеством для .
Связь с символами Кристоффеля
В псевдоримановой геометрии связность Леви -Чивиты часто записывается в терминах символов Кристоффеля вместо связности one-form . Можно определить символы Кристоффеля для связности на любом векторном расслоении, а не только на касательном расслоении псевдориманова многообразия. Для этого предположим, что в дополнение к тому, что это тривиализирующее открытое подмножество для векторного расслоения , это также локальная карта для многообразия , допускающая локальные координаты .
В такой локальной карте существует выделенная локальная структура для дифференциальных одноформ, заданных как , и локальные одноформы связи могут быть расширены в этом базисе как
для набора локальных гладких функций , называемых символами Кристоффеля над . В случае, когда и является связностью Леви-Чивиты, эти символы в точности совпадают с символами Кристоффеля из псевдоримановой геометрии.
Выражение для того, как действует в локальных координатах, можно далее расширить с помощью локальной карты и символов Кристоффеля, получив его в виде
Свертывание этого выражения с касательным вектором локальной координаты приводит к
Это определяет набор локально определенных операторов.
с тем свойством, что
Изменение местной тривиализации
Предположим, что есть другой выбор локальной системы отсчета над тем же самым тривиализующим множеством , так что существует матрица гладких функций, связывающих и , определяемая как
Прослеживая построение локальной формы связи для фрейма , можно обнаружить, что одноформа связи для задается выражением
где обозначает обратную матрицу к . В матричной записи это можно записать
где — матрица единичных форм, полученная путем взятия внешней производной матрицы покомпонентно.
В случае, когда — касательное расслоение, а — якобиан преобразования координат , длинные формулы для преобразования символов Кристоффеля связности Леви-Чивиты можно восстановить из более кратких законов преобразования приведенной выше формы связности.
Параллельный перенос и голономия
Связность на векторном расслоении определяет понятие параллельного переноса на вдоль кривой в . Пусть будет гладким путем в . Участок вдоль называется параллельным , если
для всех . Эквивалентно, можно рассмотреть обратный пучок для . Это векторное расслоение над с волокном над . Соединение на тянет обратно к соединению на . Раздел из параллелен тогда и только тогда, когда .
Предположим , что есть путь от до в . Уравнение выше, определяющее параллельные секции, является обыкновенным дифференциальным уравнением первого порядка (ср. локальное выражение выше) и поэтому имеет единственное решение для каждого возможного начального условия. То есть, для каждого вектора в существует уникальная параллельная секция с . Определить карту параллельного переноса
Можно показать, что является линейным изоморфизмом , причем обратный задается путем выполнения той же процедуры с обратным путем от до .
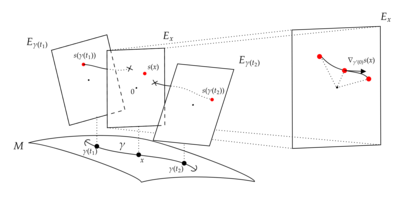
Параллельный перенос можно использовать для определения группы голономии соединения, основанного на точке в . Это подгруппа, состоящая из всех отображений параллельного переноса, исходящих из циклов, основанных на :
Группа голономии связности тесно связана с кривизной связности (AmbroseSinger 1953).
Связь может быть восстановлена из ее параллельных транспортных операторов следующим образом. Если — векторное поле и сечение, в точке выберите интегральную кривую для при . Для каждого мы запишем для параллельного транспортного отображения, движущегося вдоль от до . В частности, для каждого , мы имеем . Затем определяет кривую в векторном пространстве , которая может быть дифференцирована. Ковариантная производная восстанавливается как
Это показывает, что эквивалентное определение связи дается путем указания всех параллельных транспортных изоморфизмов между волокнами и принятия приведенного выше выражения в качестве определения .
Кривизна
Кривизна связности на является 2-формой на со значениями в расслоении эндоморфизмов . То есть,
Он определяется выражением
где и являются касательными векторными полями на и является сечением . Необходимо проверить, что является -линейным по обоим и и что он фактически определяет эндоморфизм расслоения .
Как упоминалось выше, ковариантная внешняя производная не обязательно должна быть равна нулю при действии на -значные формы. Однако оператор строго тензорен (т.е. -линейен). Это подразумевает, что он индуцируется из 2-формы со значениями в . Эта 2-форма является в точности формой кривизны, приведенной выше. Для -значной формы мы имеем
Плоское соединение — это соединение, форма кривизны которого тождественно равна нулю.
Локальная форма и структурное уравнение Картана
Форма кривизны имеет локальное описание, называемое структурным уравнением Картана . Если имеет локальную форму на некотором тривиализирующем открытом подмножестве для , то
на . Чтобы прояснить эту нотацию, заметим, что является эндоморфно-значной одноформой, и поэтому в локальных координатах принимает форму матрицы одноформ. Операция применяет внешнюю производную покомпонентно к этой матрице и обозначает матричное умножение, где компоненты вклиниваются, а не умножаются.
В локальных координатах на , если форма связи записана для набора локальных эндоморфизмов , то имеем
Дальнейшее расширение этого в терминах символов Кристоффеля приводит к знакомому выражению из римановой геометрии. А именно, если является сечением над , то
Здесь — полный тензор кривизны , а в римановой геометрии отождествляется с римановым тензором кривизны .
Можно проверить, что если мы определим как клиновидное произведение форм, но коммутатор эндоморфизмов, а не композицию, то и с этой альтернативной записью уравнение структуры Картана примет вид
Эта альтернативная нотация обычно используется в теории главных связностей расслоений, где вместо этого мы используем форму связности , -однозначную форму алгебры Ли , для которой нет понятия композиции (в отличие от случая эндоморфизмов), но есть понятие скобки Ли.
В некоторых источниках (см., например, (MadsenTornehave1997)) уравнение структуры Картана может быть записано со знаком минус:
Это другое соглашение использует порядок умножения матриц, который отличается от стандартной записи Эйнштейна в клиновом произведении матричнозначных единичных форм.
Идентичность Бьянки
Версия второго (дифференциального) тождества Бьянки из римановой геометрии справедлива для связности на любом векторном расслоении. Напомним, что связность на векторном расслоении индуцирует эндоморфную связность на . Эта эндоморфная связность сама по себе имеет внешнюю ковариантную производную, которую мы неоднозначно называем . Поскольку кривизна является глобально определенной -значной двумерной формой, мы можем применить к ней внешнюю ковариантную производную. Тождество Бьянки утверждает, что
- .
Это лаконично отражает сложные тензорные формулы тождества Бианки в случае римановых многообразий, и можно перейти от этого уравнения к стандартным тождествам Бианки, расширив связность и кривизну в локальных координатах.
В общем случае нет аналога первого ( алгебраического) тождества Бьянки для общей связности, поскольку это использует специальные симметрии связности Леви-Чивиты. А именно, используется то, что индексы векторного расслоения в тензоре кривизны могут быть заменены индексами кокасательного расслоения, полученными из после использования метрики для понижения или повышения индексов. Например, это позволяет определить условие отсутствия кручения для связности Леви-Чивиты, но для общего векторного расслоения -индекс относится к локальному базису координат , а -индексы - к локальной системе координат и полученными из расщепления . Однако в особых обстоятельствах, например, когда ранг равен размерности и выбрана форма пайки , можно использовать пайку для замены индексов и определения понятия кручения для аффинных связностей, которые не являются связностью Леви-Чивиты.
Калибровочные преобразования
Если даны две связи на векторном расслоении , естественно спросить, когда их можно считать эквивалентными. Существует четко определенное понятие автоморфизма векторного расслоения . Сечение является автоморфизмом, если обратимо в каждой точке . Такой автоморфизм называется калибровочным преобразованием , а группа всех автоморфизмов называется калибровочной группой , часто обозначаемой или . Группа калибровочных преобразований может быть аккуратно охарактеризована как пространство сечений заглавного A присоединенного расслоения каркасного расслоения векторного расслоения . Это не следует путать со строчной буквой a присоединенного расслоения , которое естественным образом отождествляется с самим собой. Расслоение является ассоциированным расслоением к главному каркасному расслоению посредством представления сопряжения на себе, , и имеет волокно той же общей линейной группы , где . Обратите внимание, что, несмотря на то же волокно, что и каркасное расслоение , и будучи ассоциированным с ним, не равно каркасному расслоению и даже самому главному расслоению. Калибровочная группа может быть эквивалентно охарактеризована как
Калибровочное преобразование действует на сечения , и, следовательно, действует на соединения сопряжением. Явно, если есть соединение на , то определяется как
для . Чтобы проверить, что это соединение, проверяется правило продукта
Можно проверить, что это определяет левое групповое действие на аффинном пространстве всех связей .
Так как является аффинным пространством, смоделированным на , должна существовать некоторая эндоморфно-значная одноформа такая, что . Используя определение эндоморфизма связи, индуцированного , можно увидеть, что
то есть сказать, что .
Говорят, что две связности калибровочно эквивалентны , если они отличаются действием калибровочной группы, а факторпространство является пространством модулей всех связностей на . В общем случае это топологическое пространство не является ни гладким многообразием, ни даже хаусдорфовым пространством , но содержит внутри себя пространство модулей связностей Янга–Миллса на , которое представляет значительный интерес в калибровочной теории и физике .
Примеры
- Классическая ковариантная производная или аффинная связность определяет связность на касательном расслоении M или, в более общем смысле, на любом тензорном расслоении, образованном взятием тензорных произведений касательного расслоения на себя и на свое двойственное .
- Соединение можно явно описать как оператор
- где внешняя производная вычисляется на векторнозначных гладких функциях и являются гладкими. Раздел может быть идентифицирован с картой
- а потом
- Если расслоение снабжено метрикой расслоения , внутренним произведением его векторных волокон, то метрическая связь определяется как связь, совместимая с метрикой расслоения.
- Связь Янга-Миллса — это специальная метрическая связь , которая удовлетворяет уравнениям движения Янга-Миллса .
- Риманова связность — это метрическая связность на касательном расслоении риманова многообразия .
- Связность Леви-Чивиты — это специальная риманова связность: совместимая с метрикой связность на касательном расслоении, которая также не имеет кручения . Она уникальна в том смысле, что для любой римановой связности всегда можно найти одну и только одну эквивалентную связность, которая не имеет кручения. «Эквивалентная» означает, что она совместима с той же метрикой, хотя тензоры кривизны могут быть разными; см. телепараллелизм . Разница между римановой связностью и соответствующей связностью Леви-Чивиты задается тензором конторсии .
- Внешняя производная является плоской связностью на (тривиальном линейном расслоении над M ).
- В более общем случае на любом плоском векторном расслоении (т.е. векторном расслоении, все функции перехода которого постоянны) существует каноническая плоская связность , которая задается внешней производной в любой тривиализации.
Смотрите также
Ссылки
- Черн, Шиинг-Шен (1951), Темы дифференциальной геометрии , Институт перспективных исследований, мимеографированные записи лекций
- Дарлинг, RWR (1994), Дифференциальные формы и соединения , Кембридж, Великобритания: Cambridge University Press, Bibcode : 1994dfc..book.....D, ISBN 0-521-46800-0
- Кобаяси, Сёсичи; Номидзу, Кацуми (1996) [1963], Основы дифференциальной геометрии, т. 1 , Библиотека классических произведений Wiley, Нью-Йорк: Wiley Interscience , ISBN 0-471-15733-3
- Кошул, Дж.Л. (1950), «Гомология и когомологии алгебр Ли», Bulletin de la Société Mathématique de France , 78 : 65–127, doi : 10.24033/bsmf.1410
- Уэллс, РО (1973), Дифференциальный анализ на комплексных многообразиях , Springer-Verlag, ISBN 0-387-90419-0
- Эмброуз, У.; Сингер, И.М. (1953), «Теорема о голономии», Труды Американского математического общества , 75 (3): 428–443, doi : 10.2307/1990721 , JSTOR 1990721
- Дональдсон, С. К. и Кронхаймер, П. Б., 1997. Геометрия четырехмерных многообразий. Oxford University Press.
- Ту, Л. В., 2017. Дифференциальная геометрия: связности, кривизна и характеристические классы (т. 275). Springer.
- Таубс, CH, 2011. Дифференциальная геометрия: расслоения, связности, метрики и кривизна (т. 23). OUP Oxford.
- Ли, Дж. М. (2018), Введение в римановы многообразия , Graduate Texts in Mathematics, т. 176, doi : 10.1007/978-3-319-91755-9, ISBN 978-3-319-91754-2
- Мэдсен, И. Х.; Торнехейв, Дж. (1997), От исчисления к когомологиям: когомологии де Рама и характеристические классы , Cambridge University Press



















































































































































































![{\displaystyle \gamma :[0,1]\to M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0066953642fb00abb394327531cea098815cd1c8)

![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)

![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)






















![{\displaystyle F_{\nabla }(X,Y)(s)=\nabla _{X} \nabla _{Y}s-\nabla _{Y}\nabla _{X}s-\nabla _{[ X,Y]}с}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f59042b065edd05300ca109d93fe0d5b9537b96d)










![{\displaystyle F_{\nabla}=\sum _{p,q=1}^{n}{\frac {1}{2}}\left({\frac {\partial A_{q}}{\partial x^{p}}}-{\frac {\partial A_{p}}{\partial x^{q}}}+[A_{p},A_{q}]\right)dx^{p}\wedge dx^{q}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45e8d584b3732866710e9d1a066d866c42bb633)




![{\displaystyle [А,А]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b8f9de22f28fafb483e8f47e20ca0046206b5e6)
![{\displaystyle A\wedge A={\frac {1}{2}}[A,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/793044c51a2a65137eaec786a1e6842bdc89b11c)
![{\displaystyle F_{\nabla }=dA+{\frac {1}{2}}[A,A].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a8d81a9efc378e6914d6e299fcfae517ec64c39)






































