Усеченная треугольная мозаика порядка 7

Усеченная треугольная мозаика порядка 7
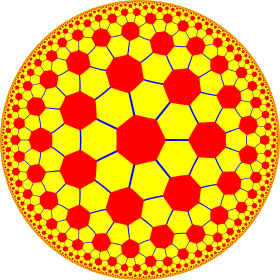Модель диска Пуанкаре гиперболической плоскости
Тип	Гиперболическая однородная мозаика
Конфигурация вершины	7.6.6
Символ Шлефли	т{3,7}
Символ Витхоффа	2 7 \| 3
Диаграмма Коксетера
Группа симметрии	[7,3], (*732)
Двойной	Гептакис — семиугольная мозаика
Характеристики	Вершинно-транзитивный

В геометрии усеченная треугольная мозаика порядка 7 , иногда называемая гиперболическим футбольным мячом , ^[1] является полуправильной мозаикой гиперболической плоскости. На каждой вершине есть два шестиугольника и один семиугольник , образуя узор, похожий на обычный футбольный мяч ( усеченный икосаэдр ) с семиугольниками вместо пятиугольников . Он имеет символ Шлефли t{3,7}.

Гиперболический футбольный мяч (футбол)

Эта мозаика называется гиперболическим футбольным мячом (футбольным мячом) из-за ее сходства с рисунком усеченного икосаэдра, используемым на футбольных мячах. Небольшие ее части как гиперболической поверхности могут быть построены в 3-мерном пространстве.

Усеченный икосаэдр как многогранник и шар	Эвклидова шестиугольная мозаика, раскрашенная как усеченная треугольная мозаика	Бумажная конструкция гиперболического футбольного мяча.

Двойная плитка

Двойственная мозаика называется гептакис-семиугольной мозаикой , названной так потому, что ее можно построить как семиугольную мозаику , в которой каждый семиугольник разделен центральной точкой на семь треугольников.

Связанные плитки

Эта гиперболическая мозаика топологически связана как часть последовательности однородных усеченных многогранников с конфигурациями вершин (n.6.6) и симметрией группы Кокстера [n,3].

* n 32 мутация симметрии усеченных мозаик: n .6.6 в т е
Сим. * н 42 [н,3]	Сферический				Евклид.	Компактный		Парак.	Некомпактный гиперболический
Сим. * н 42 [н,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i,3]	[9и,3]	[6i,3]
Усеченные фигуры
Конфигурация.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n-kis цифры
Конфигурация.	В2.6.6	В3.6.6	В4.6.6	В5.6.6	В6.6.6	В7.6.6	В8.6.6	В∞.6.6	V12i.6.6	V9i.6.6	V6i.6.6

Согласно построению Витхоффа, существует восемь гиперболических однородных мозаик , которые могут быть основаны на правильной семиугольной мозаике.

Если раскрасить плитки красным цветом на исходных гранях, желтым — на исходных вершинах и синим — вдоль исходных ребер, то получится 8 форм.

Однородные семиугольные/треугольные мозаики в т е
Симметрия: $[7,3], (*732)$							$[7,3] +, (732)$


${7,3}$	$т{7,3}$	$г{7,3}$	$т{3,7}$	${3,7}$	$рр{7,3}$	$тр{7,3}$	$ср{7,3}$
Равномерные дуалы


$В7 3$	$В3.14.14$	$В3.7.3.7$	$В6.6.7$	$В3 7$	$В3.4.7.4$	$В4.6.14$	$В3.3.3.3.7$

В популярной культуре

Такая мозаика занимает видное место в HyperRogue .

Смотрите также

Ссылки

^ КАК ПОСТРОИТЬ СВОЮ СОБСТВЕННУЮ МОДЕЛЬ ГИПЕРБОЛИЧЕСКОГО ФУТБОЛЬНОГО МЯЧА

Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 19, Гиперболические архимедовы мозаики)
"Глава 10: Регулярные соты в гиперболическом пространстве". Красота геометрии: Двенадцать эссе . Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

Внешние ссылки

Вайсштейн, Эрик В. "Гиперболическая мозаика". MathWorld .
Вайсштейн, Эрик В. "Гиперболический диск Пуанкаре". MathWorld .
Галерея гиперболических и сферических мозаик
KaleidoTile 3: Образовательное программное обеспечение для создания сферических, плоских и гиперболических мозаик
Гиперболические плоские мозаики, Дон Хэтч
Геометрические исследования гиперболического футбольного мяча Фрэнка Соттиле

[1] КАК ПОСТРОИТЬ СВОЮ СОБСТВЕННУЮ МОДЕЛЬ ГИПЕРБОЛИЧЕСКОГО ФУТБОЛЬНОГО МЯЧА