Кубогемиоктаэдр
| Кубогемиоктаэдр | |
|---|---|
 | |
| Тип | Однородный звездчатый многогранник |
| Элементы | F = 10, E = 24 V = 12 (χ = −2) |
| Лица по сторонам | 6{4}+4{6} |
| Диаграмма Коксетера |     (двойное покрытие) |
| Символ Витхоффа | 4/3 4 | 3 (двойное покрытие) |
| Группа симметрии | О , ч , [4,3], *432 |
| Индекс ссылок | У 15 , С 51 , Ж 78 |
| Двойной многогранник | Гексагемиооктакрон |
| Вершинная фигура |  4.6.4/3.6 |
| Акроним Bowers | Чо |
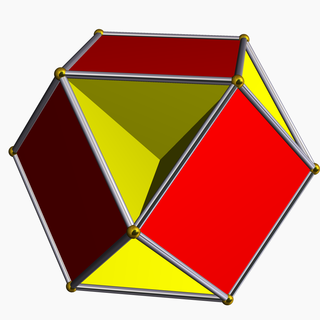
В геометрии кубогемиоктаэдр — невыпуклый однородный многогранник , индексируемый как U 15 . Он имеет 10 граней (6 квадратов и 4 правильных шестиугольника ), 24 ребра и 12 вершин. [1] Его вершинная фигура — скрещенный четырехугольник .
Ему присвоен символ Витхоффа 4 ⁄ 3 4 | 3 , хотя это двойное накрытие этой фигуры.
Невыпуклый многогранник имеет пересекающиеся грани, которые не представляют собой новые ребра или грани. На рисунке вершины обозначены золотыми сферами, а ребра — серебряными цилиндрами.
Это полумногогранник с 4 шестиугольными гранями, проходящими через центр модели. Шестиугольники пересекаются друг с другом, поэтому видны только треугольные части каждого.
Связанные многогранники
Он имеет такое же расположение вершин и ребер, как кубооктаэдр (имеющий общие квадратные грани) и октагемиоктаэдр (имеющий общие шестиугольные грани).
 Кубооктаэдр | Кубогемиоктаэдр |  Октагемиоктаэдр |
Тетрагексагональная мозаика
Кубогемиоктаэдр можно рассматривать как развертку на гиперболической тетрагексагональной мозаике с вершинной фигурой 4.6.4.6.
Гексагемиооктакрон
| Гексагемиооктакрон | |
|---|---|
 | |
| Тип | Звездчатый многогранник |
| Лицо | — |
| Элементы | F = 12, E = 24 V = 10 (χ = −2) |
| Группа симметрии | О , ч , [4,3], *432 |
| Индекс ссылок | ДУ 15 |
| двойной многогранник | Кубогемиоктаэдр |
Гексагемиооктакрон является дуальным кубогемиооктаэдром и одним из девяти дуальных гемиполиэдров . Он визуально неотличим от октагемиоктакрона .
Поскольку кубогемиоктаэдр имеет четыре шестиугольные грани, проходящие через центр модели, он является вырожденным и может рассматриваться как имеющий четыре вершины, удаленные на бесконечность.
В «Двойственных моделях » Магнуса Веннингера они представлены пересекающимися бесконечными призмами, проходящими через центр модели, обрезанными в определенной точке, удобной для создателя.
Смотрите также
- Полукуб - четыре вершины на бесконечности направленно соответствуют четырем вершинам этого абстрактного многогранника.
Ссылки
- ^ Мейдер, Роман. "15: кубогемиоктаэдр". MathConsult .
- Веннингер, Магнус (1983), Двойные модели , Cambridge University Press , doi : 10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, МР 0730208(Страница 101, Двойственные (девяти) полумногогранники)
Внешние ссылки
- Вайсштейн, Эрик В. «Гексахемиоктакрон». MathWorld .
- Вайсштейн, Эрик В. , «Кубогемиоктаэдр» («Однородный многогранник») на MathWorld .
- Однородные многогранники и двойственные им многогранники
 | Эта статья о многогранниках — заглушка . Вы можете помочь Википедии, расширив ее. |
