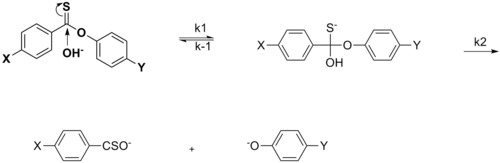
Уравнение Гаммета
В органической химии уравнение Гаммета описывает линейное соотношение свободной энергии, связывающее скорости реакции и константы равновесия для многих реакций с участием производных бензойной кислоты с мета- и пара -заместителями друг с другом всего с двумя параметрами: константой заместителя и константой реакции. [1] [2] Это уравнение было разработано и опубликовано Луисом Плаком Гамметом в 1937 году [3] как продолжение качественных наблюдений в его публикации 1935 года. [4]
Основная идея заключается в том, что для любых двух реакций с двумя ароматическими реагентами, отличающимися только типом заместителя, изменение свободной энергии активации пропорционально изменению свободной энергии Гиббса . [5] Это понятие не следует из элементарной термохимии или химической кинетики и было введено Гамметом интуитивно. [a]
Основное уравнение:
где
- = Справочная константа
- = Константа заместителя
- = Константа скорости реакции
связывающая константу равновесия , , для данной равновесной реакции с заместителем R и опорную константу , когда R является атомом водорода, с константой заместителя σ , которая зависит только от конкретного заместителя R, и константой скорости реакции ρ , которая зависит только от типа реакции, но не от используемого заместителя. [4] [3]
Уравнение справедливо также для скоростей реакции k ряда реакций с замещенными производными бензола:
В этом уравнении — опорная скорость реакции незамещенного реагента, а k — скорость замещенного реагента.
График зависимости для заданного равновесия от заданной скорости реакции со многими по-разному замещенными реагентами даст прямую линию.
Константы заместителей
Начальной точкой для сбора констант заместителей является химическое равновесие , для которого константа заместителя произвольно принимается равной 0, а константа реакции принимается равной 1: депротонирование бензойной кислоты или бензолкарбоновой кислоты (R и R' оба H) в воде при 25 °C.

| Заместитель | пара- эффект | мета- эффект |
|---|---|---|
| Диметиламино | −0,83 | −0,211 |
| Амино | −0,66 | −0,161 |
| Бутиламино | −0,51 | −0,34 |
| Гидрокси | −0,37 | +0,12 |
| Метокси | −0,268 | +0,115 |
| Этокси | −0,25 | +0,015 |
| Метил | −0,170 | −0,069 |
| Триметилсилил | −0,07 | −0,04 |
| Никто | 0.000 | 0.000 |
| Фтор | +0,062 | +0,337 |
| Хлоро | +0,227 | +0,373 |
| Бром | +0,232 | +0,393 |
| Иодо | +0,276 | +0,353 |
| Этоксикарбонил | +0,45 | +0,37 |
| Трифторметил | +0,54 | +0,43 |
| Циано | +0,66 | +0,56 |
| Нитро | +0,778 | +0,710 |
Получив значение для K 0 , теперь определяется ряд констант равновесия (K) на основе того же процесса, но теперь с изменением пара-заместителя — например, п-гидроксибензойной кислоты (R=OH, R'=H) или п-аминобензойной кислоты (R=NH 2 , R'=H) . Эти значения, объединенные в уравнении Гаммета с K 0 и учитывая, что ρ = 1, дают константы пара-заместителя, собранные в таблице 1 для амина , метокси , этокси , диметиламино , метила , фтора , брома , хлора , йода , нитро и циано -заместителей. Повторение процесса с мета-заместителями дает константы мета-заместителя . Эта обработка не включает орто-заместители , которые внесли бы стерические эффекты .
Значения σ, представленные в таблице выше, показывают определенные эффекты заместителей. При ρ = 1 группа заместителей с увеличивающимися положительными значениями — в частности, циано и нитро — приводит к увеличению константы равновесия по сравнению с водородным эталоном, что означает, что кислотность карбоновой кислоты (изображенной в левой части уравнения) увеличилась. Эти заместители стабилизируют отрицательный заряд на атоме кислорода карбоксилата посредством индуктивного эффекта оттягивания электронов (-I), а также посредством отрицательного мезомерного эффекта (-M).
Следующий набор заместителей — галогены , для которых эффект заместителя все еще положителен, но гораздо скромнее. Причина этого в том, что в то время как индуктивный эффект все еще отрицателен, мезомерный эффект положителен, вызывая частичную отмену. Данные также показывают, что для этих заместителей мета-эффект намного больше, чем пара-эффект, из-за того, что мезомерный эффект значительно снижен в мета-заместителе. В случае мета-заместителей атом углерода, несущий отрицательный заряд, находится дальше от группы карбоновой кислоты (структура 2b).
Этот эффект изображен на схеме 3 , где в паразамещенном арене 1a одна резонансная структура 1b представляет собой хиноид с положительным зарядом на заместителе X, высвобождая электроны и тем самым дестабилизируя заместитель Y. Этот дестабилизирующий эффект невозможен, когда X имеет мета-ориентацию.

Другие заместители, такие как метокси и этокси , могут даже иметь противоположные знаки для константы заместителя в результате противоположного индуктивного и мезомерного эффекта. Только алкильные и арильные заместители, такие как метил, являются электрон-высвобождающими в обоих отношениях.
Конечно, когда знак константы реакции отрицательный (следующий раздел), только заместители с такой же отрицательной константой замещения будут увеличивать константы равновесия.
Theσ п–иσ п+константы
Поскольку карбонильная группа не может служить источником электронов для групп -M (в отличие от доноров неподеленных пар, таких как OH), для реакций с участием исходных материалов фенола и анилина значения σ p для электроноакцепторных групп будут казаться слишком малыми. Для реакций, где ожидается, что резонансные эффекты будут иметь большое влияние, модифицированный параметр и модифицированный набор констант σ p – могут дать лучшее соответствие. Этот параметр определяется с использованием констант ионизации паразамещенных фенолов с помощью масштабного коэффициента для сопоставления значений σ p – со значениями σ p для «неаномальных» заместителей, чтобы поддерживать сопоставимые значения ρ: для ArOH ⇄ ArO – + H + мы определяем .
Аналогично, карбонильный углерод бензойной кислоты находится в узловом положении и не может служить стоком для групп +M (в отличие от карбокатиона в бензильном положении). Таким образом, для реакций с участием карбокатионов в α-положении значения σ p для электронодонорных групп будут казаться недостаточно отрицательными. Исходя из аналогичных соображений, набор констант σ p + дает лучшее соответствие для реакций с участием электронодонорных групп в пара -положении и образованием карбокатиона в бензильном положении. σ p + основаны на константах скорости реакции S N 1 кумилхлоридов в 90% ацетоне/воде: для ArCMe 2 Cl + H 2 O → ArCMe 2 OH + HCl мы определяем . Обратите внимание, что масштабный коэффициент отрицателен, поскольку электронодонорная группа ускоряет реакцию. Для реакции, для которой строится график Гаммета, может потребоваться проверка этих альтернативных констант Гаммета, чтобы увидеть, можно ли получить лучшую линейность.
Значение Rho
Зная константы заместителей, теперь можно получить константы реакции для широкого спектра органических реакций . Архетипической реакцией является щелочной гидролиз этилбензоата (R=R'=H) в смеси вода/этанол при 30 °C. Измерение скорости реакции k 0 в сочетании с измерением многих замещенных этилбензоатов в конечном итоге приводит к константе реакции +2,498. [3] [ требуется обновление ] [ необходим непервичный источник ]

Константы реакции известны для многих других реакций и равновесий. Вот выборка из них, предоставленная самим Хэмметом (со значениями в скобках):
- гидролиз замещенного эфира коричной кислоты в этаноле/воде (+1,267)
- ионизация замещенных фенолов в воде (+2,008)
- катализируемая кислотой этерификация замещенных бензойных эфиров в этаноле (-0,085)
- кислотно-катализируемое бромирование замещенных ацетофенонов ( галогенирование кетонов ) в уксусной кислоте /воде/ соляной кислоте (+0,417)
- гидролиз замещенных бензилхлоридов в ацетоне -воде при 69,8 °С (-1,875).
Константа реакции, или константа чувствительности, ρ , описывает восприимчивость реакции к заместителям по сравнению с ионизацией бензойной кислоты. Она эквивалентна наклону графика Гаммета. Информация о реакции и связанном с ней механизме может быть получена на основе полученного значения для ρ . Если значение:
- ρ>1 , реакция более чувствительна к заместителям, чем бензойная кислота, и в ходе реакции образуется отрицательный заряд (или теряется положительный заряд).
- 0<ρ<1 реакция менее чувствительна к заместителям, чем бензойная кислота, и образуется отрицательный заряд (или теряется положительный заряд).
- ρ=0 , чувствительность к заместителям отсутствует, заряд не накапливается и не теряется.
- ρ<0 , реакция создает положительный заряд (или теряет отрицательный заряд).
Эти соотношения можно использовать для выяснения механизма реакции. Поскольку значение ρ связано с зарядом на этапе определения скорости, на основе этой информации можно разработать механизмы. Если предполагается, что механизм реакции ароматического соединения происходит через один из двух механизмов, соединение можно модифицировать с помощью заместителей с различными значениями σ и провести кинетические измерения. После проведения этих измерений можно построить график Гаммета для определения значения ρ. Если один из этих механизмов включает образование заряда, это можно проверить на основе значения ρ . И наоборот, если график Гаммета показывает, что заряд не развивается, т. е. нулевой наклон, механизм, включающий создание заряда, можно отбросить.
Графики Гаммета не всегда могут быть идеально линейными. Например, кривая может показывать внезапное изменение наклона или значения ρ . В таком случае, вероятно, механизм реакции изменится при добавлении другого заместителя. Другие отклонения от линейности могут быть вызваны изменением положения переходного состояния. В такой ситуации некоторые заместители могут привести к тому, что переходное состояние появится раньше (или позже) в механизме реакции. [7] [ нужна страница ]
Доминирующие электронные эффекты
Преобладают 3 вида основного состояния или статических электрических воздействий:
- Резонансный (мезомерный) эффект
- Индуктивный эффект : электрическое влияние группы, которое передается в основном посредством поляризации связывающих электронов от одного атома к другому.
- Прямой электростатический (полевой) эффект: электрическое влияние полярного или диполярного заместителя , которое передается в первую очередь к реакционноспособной группе через пространство (включая растворитель , если таковой имеется) в соответствии с законами классической электростатики.
Последние два влияния часто рассматриваются вместе как составной эффект, но здесь они рассматриваются отдельно. Вестхаймер продемонстрировал, что электрические эффекты π-замещенных диполярных групп на кислотность бензойной и фенилуксусной кислот могут быть количественно коррелированы, предполагая только прямое электростатическое действие заместителя на ионизируемый протон карбоксильной группы . Обработка Вестхаймера работала хорошо, за исключением тех кислот с заместителями, которые имеют неподеленные электронные пары, такие как –OH и –OCH3, поскольку эти заместители сильно взаимодействуют с бензольным кольцом. [8] [ требуется непервичный источник ] [ требуется непервичный источник ] [9] [ требуется непервичный источник ] [ требуется обновление ] [ требуется непервичный источник ]
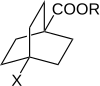
Робертс и Морленд изучали реакционную способность 4-замещенных бицикло[2.2.2]октан-1-карбоновых кислот и эфиров. В такой молекуле передача электрических эффектов заместителей через кольцо путем резонанса невозможна. Следовательно, это намекает на роль π-электронов в передаче эффектов заместителей через ароматические системы . [10] [ требуется непервичный источник ] [ требуется непервичный источник ]
Реакционная способность 4-замещенных бицикло[2.2.2]октан-1-карбоновых кислот и эфиров измерялась в 3 различных процессах, каждый из которых ранее использовался с производными бензойной кислоты. График log(k) против log(K A ) показал линейную зависимость. Такие линейные зависимости соответствуют линейным зависимостям свободной энергии, которые настоятельно подразумевают, что влияние заместителей проявляется через изменения потенциальной энергии и что стерические и энтропийные члены остаются почти постоянными на протяжении ряда. Линейная зависимость хорошо укладывается в уравнение Гаммета. Для 4-замещенных производных бицикло[2.2.2.]октан-1-карбоновой кислоты константы заместителя и реакции обозначены как σ' и ρ'.
Сравнение ρ и ρ'
| Реакция [ необходима ссылка ] | ρ' | ρ | Д е |
|---|---|---|---|
| Ионизация кислот | 1.464 | 1.464 | 54 |
| Щелочной гидролиз этиловых эфиров | 2.24 | 2.494 | 28 |
| Кислоты с дифенилдиазометаном | 0,698 | 0,937 | 24 |
Данные по реакционной способности указывают на то, что влияние групп заместителей на реакционную способность замещенных бензойных и бицикло[2.2.2.]-октан-1-карбоновых кислот сопоставимо. Это означает, что ароматические π-электроны не играют доминирующей роли в передаче электрических эффектов диполярных групп на ионизуемую карбоксильную группу. Разница между ρ и ρ' для реакций кислот с дифенилазометаном, вероятно, обусловлена обратной зависимостью от диэлектрической проницаемости растворителя D e
Сравнение σ и σ'
This section cites its sources but its page reference ranges are too broad or incorrect. (June 2015) |
| Заместитель | σ' [ необходима ссылка ] | σ пара c | σ мета с | σ пара − σ' [ необходима ссылка ] | σ мета − σ' [ необходима ссылка ] |
|---|---|---|---|---|---|
| ЧАС | 0 | 0 | 0 | 0 | 0 |
| ОЙ | 0,283 | −0,341 | 0,014 | −0,624 | −0,269 |
| CO2C2H5 | 0,297 | 0,402 | 0.334 | 0,105 | 0,037 |
| Бр | 0,454 | 0,232 | 0,391 | −0,222 | −0,063 |
| КН | 0,579 | 0,656 | 0,608 | 0,077 | 0,029 |
Для мета-направляющих групп ( электроноакцепторная группа или EWG ) σ мета и σ пара более положительны, чем σ'. (Верхний индекс, c, в таблице обозначает данные из Hammett, 1940. [11] [ нужна страница ] ) Для орто-пара-направляющих групп ( электронодонорная группа или EDG ) σ' более положительны, чем σ мета и σ пара . Разница между σ пара и σ' (σ пара – σ') больше, чем между σ мета и σ'(σ мета – σ'). Это ожидаемо, поскольку эффекты электронного резонанса ощущаются сильнее в p-положениях. Значения (σ – σ') можно принять в качестве разумной меры эффектов резонанса.
Нелинейность
This section may require cleanup to meet Wikipedia's quality standards. The specific problem is: the images in the section are too loosely tied to the text, e.g., there is no mention of sulfinate ester or imine hydrolysis, though this is what the schemes present, and there are no sources indicated for the schemes, violating either WP:OR or WP:VERIFY. (June 2015) |
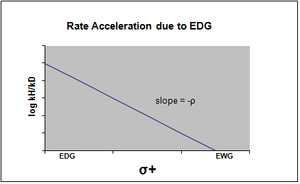
График уравнения Гаммета обычно рассматривается как линейный, с положительным или отрицательным наклоном, коррелирующим со значением rho. Однако нелинейность возникает на графике Гаммета, когда заместитель влияет на скорость реакции или изменяет определяющий скорость этап или механизм реакции. По причине первого случая были введены новые константы сигма, чтобы учесть отклонение от линейности, которое в противном случае наблюдалось бы в результате влияния заместителя. σ+ учитывает накопление положительного заряда, происходящее в переходном состоянии реакции. Следовательно, электронодонорная группа (EDG) ускорит скорость реакции за счет резонансной стабилизации и даст следующий график сигма с отрицательным значением rho. [12] [ требуется непервичный источник ] [ требуется непервичный источник ]
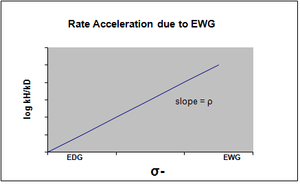
σ- обозначается в случае, когда в переходном состоянии происходит накопление отрицательного заряда, и скорость реакции, следовательно, ускоряется группами, оттягивающими электроны (EWG). EWG оттягивает электронную плотность посредством резонанса и эффективно стабилизирует образующийся отрицательный заряд. Соответствующий график покажет положительное значение rho.
В случае нуклеофильного ацильного замещения эффект заместителя X не уходящей группы может фактически ускорить скорость реакции нуклеофильного присоединения, когда X является EWG. Это объясняется резонансным вкладом EWG в отвод электронной плотности, тем самым увеличивая восприимчивость к нуклеофильной атаке на карбонильный углерод. Изменение скорости происходит, когда X является EDG, как это видно при сравнении скоростей между X = Me и X = OMe, и нелинейность наблюдается на графике Гаммета. [13] [ требуется непервичный источник ] [ требуется непервичный источник ]
Эффект заместителя может изменить скорость-определяющий шаг (rds) в механизме реакции. Определенный электронный эффект может ускорить определенный шаг так, что он больше не будет rds. [14] [ требуется непервичный источник ] [ требуется непервичный источник ]

Изменение механизма реакции также приводит к нелинейности на графике Гаммета. Обычно модель, используемая для измерения изменений скорости в этом случае, — это модель реакции SN2. [15] [ требуется непервичный источник ] [ требуется непервичный источник ] Однако было замечено, что в некоторых случаях реакции SN2 EWG не ускоряет реакцию, как можно было бы ожидать [16] [ требуется непервичный источник ] [ требуется непервичный источник ] и что скорость меняется в зависимости от заместителя. Фактически, знак заряда и степень его развития будут зависеть от заместителя в случае бензильной системы. [15] [ требуется непервичный источник ]

Например, заместитель может определять механизм как реакцию типа SN1 , а не как реакцию типа SN2 , и в этом случае полученный график Гаммета будет указывать на ускорение скорости из-за EDG, тем самым проясняя механизм реакции.
Другое отклонение от обычного уравнения Гаммета объясняется зарядом нуклеофила. [15] [ необходим непервичный источник ] Несмотря на нелинейность в бензильных реакциях SN2, электроноакцепторные группы могут либо ускорять, либо замедлять реакцию. Если нуклеофил отрицательно заряжен (например, цианид), электроноакцепторная группа увеличит скорость из-за стабилизации дополнительного заряда, который наносится на углерод в переходном состоянии. С другой стороны, если нуклеофил не заряжен (например, трифенилфосфин), электроноакцепторная группа замедлит реакцию за счет уменьшения электронной плотности на антисвязывающей орбитали уходящей группы в переходном состоянии.
модификации Хэммета
В настоящее время существуют другие уравнения, уточняющие исходное уравнение Гаммета: уравнение Суэйна–Лаптона , [ требуется ссылка ] уравнение Тафта , [ требуется ссылка ] уравнение Грюнвальда–Винштейна , [ требуется ссылка ] и уравнение Юкавы–Цуно . [ требуется ссылка ] Также было разработано уравнение, которое учитывает стереохимию в алифатических системах. [ неопределенно ] [17] [ непервичный источник необходим ] [ непервичный источник необходим ]
Оценка констант сигма Гаммета
This section may contain an excessive amount of intricate detail that may interest only a particular audience. (June 2015) |

Сдвиги энергии связи ядра и электрона (CEBE) линейно коррелируют с константами заместителя Гаммета ( σ ) в замещенных производных бензола . [18] [ необходим непервичный источник ]
| ΔCEBE ≈ κσ p | ( 1 ) |
Рассмотрим пара-дизамещенный бензол pFC 6 H 4 -Z, где Z — заместитель, такой как NH 2 , NO 2 и т. д. Атом фтора находится в пара-положении по отношению к заместителю Z в бензольном кольце. На изображении справа показаны четыре выделенных атома углерода кольца, C1( ipso ), C2( orto ), C3( meta ), C4( para ) в молекуле pFC 6 H 4 -Z. Углерод с Z определяется как C1(ipso), а фторированный углерод как C4(para). Это определение соблюдается даже для Z = H. Левая часть ( 1 ) называется сдвигом CEBE или ΔCEBE и определяется как разница между CEBE фторированного атома углерода в pFC 6 H 4 -Z и фторированного углерода в эталонной молекуле FC 6 H 5 .
| ΔCEBE ≡ CEBE(C4 в pFC 6 H 4 -Z) – CEBE(C4 в pFC 6 H 5 ) | ( 2 ) |
Правая часть уравнения 1 является произведением параметра κ и константы заместителя Гаммета в пара-положении, σp . Параметр κ определяется уравнением 3 :
| κ = 2,3 кТл ( ρ - ρ * ) | ( 3 ) |
где ρ и ρ * — константы реакции Гаммета для реакции нейтральной молекулы и ионизированной молекулы ядра соответственно. ΔCEBE кольцевых углеродов в pFC 6 H 4 -Z были рассчитаны с помощью теории функционала плотности , чтобы увидеть, как они коррелируют с σ-константами Гаммета. Линейные графики были получены, когда рассчитанные сдвиги CEBE в орто-, мета- и пара-углероде были нанесены на график против констант Гаммета σ o , σ m и σ p соответственно.
- Рассчитанное значение κ ≈ 1.
Отсюда приблизительное соответствие по числовому значению и знаку между сдвигами CEBE и соответствующей им константой Гаммета σ . [19] [ необходим непервичный источник ] [ необходим непервичный источник ]
- График рассчитанного сдвига CEBE (эВ) в зависимости от сигма-пара
- Таблица сдвигов CEBE (эВ) и сигма-пара
- График рассчитанного сдвига CEBE (эВ) в зависимости от сигма-мета
- Таблица сдвигов CEBE (эВ) и сигма-мета
- График рассчитанного сдвига CEBE (эВ) в зависимости от сигма-о
- Таблица сдвигов CEBE (эВ) и сигма-орто
Смотрите также
- Принцип Белла–Эванса–Полани
- сюжет Крейга
- Соотношение свободной энергии
- п К а
- Количественная связь структуры и активности
Примечания
- ^ Первая строка его публикации 1935 года гласит: «Идея о том, что существует некая связь между скоростью реакции и константой равновесия, является одной из наиболее настойчиво поддерживаемых и в то же время наиболее решительно отрицаемых концепций в химической теории». [4]
Ссылки
- ^ IUPAC , Compendium of Chemical Terminology , 2nd ed. (The "Gold Book") (1997). Онлайн-исправленная версия: (2006–) "Уравнение Гаммета (соотношение Гаммета)". doi :10.1351/goldbook.H02732
- ^ Кинан, Шеу Л.; Петерсон, Карл П.; Петерсон, Келли; Якобсон, Кайл (2008). «Определение константы Ро уравнения Гаммета для гидролиза эфиров п-нитрофенилбензоата». J. Chem. Educ. 85 (4): 558. Bibcode :2008JChEd..85..558K. doi :10.1021/ed085p558.
- ^ abcd Хэмметт, Луис П. (1937). «Влияние структуры на реакции органических соединений. Производные бензола». J. Am. Chem. Soc. 59 (1): 96–103. doi :10.1021/ja01280a022.
- ^ abc Louis P. Hammett (1935). «Некоторые соотношения между скоростями реакций и константами равновесия». Chem. Rev. 17 (1): 125–136. doi :10.1021/cr60056a010.
- ^ Кэри, Фрэнсис А.; Сандберг, Ричард Дж. (1983). Advanced Organic Chemistry Часть A, 2-е издание. Plenum Press. ISBN 9780306410871. OCLC 1064985344.
- ^ Значения в таблице соответствуют оригинальной публикации 1937 года и отличаются от значений, появлявшихся в последующих публикациях. Для получения дополнительных стандартных значений см.: C. Hansch; A. Leo; RW Taft (1991). "A survey of Hammett substitute constants and response and field settings". Chem. Rev. 91 (2): 165–195. doi :10.1021/cr00002a004. S2CID 97583278.
- ^ EV Anslyn & DA Dougherty, Современная физическая органическая химия, стр. TBD, Sausalito, CA, US: University Science Books, ISBN 1891389319. [ нужна страница ]
- ^ Вестхаймер ФХ (1939). «Электростатическое влияние заместителей на константы диссоциации органических кислот. IV. Ароматические кислоты». J. Am. Chem. Soc. 61 (8): 1977–1980. doi :10.1021/ja01877a012.
- ^ Kirkwood JG; Westheimer FH (1938). "Электростатическое влияние заместителей на константы диссоциации органических кислот. I [Отсутствует подзаголовок]". J. Chem. Phys. 6 (9): 506. Bibcode :1938JChPh...6..506K. doi :10.1063/1.1750302. [ нужно обновление ]
- ^ Робертс Дж. Д.; Морленд Дж. У. Т. (1953). «Электрические эффекты замещающих групп в насыщенных системах. Реакционная способность 4-замещенных бицикло [2.2.2] октан-1-карбоновых кислот». J. Am. Chem. Soc. 75 (9): 2167–2173. doi :10.1021/ja01105a045.
- ^ LPHammett, 1940, «Глава III», «Глава IV» и «Глава VII» в Physical Organic Chemistry , Нью-Йорк, США: McGraw-Hill. [ нужна страница ]
- ^ Y. Yukawa & Y. Tsuno, 1959, «Эффект резонанса в соотношении Гаммета. II. Сигма-константы в электрофильных реакциях и их взаимосвязь», Bull. Chem. Soc. Jpn. 32 :965-971, см. [1], доступ 22 июня 2015 г.
- ^ Um, Ik-Hwan; Lee, Ji-Youn; Kim, Han-Tae; Bae, Sun-Kun (2004). «Кривая диаграмма Гаммета при щелочном гидролизе O -арилтионобензоатов: изменение скорости-определяющего этапа в зависимости от стабилизации основного состояния». J. Org. Chem. 69 (7): 2436–2441. doi :10.1021/jo035854r. PMID 15049643.
- ^ Харт, Х.; Седор, Эдвард А. (1967). «Механизм циклодегидратации 2-фенилтриарилкарбинолов». J. Am. Chem. Soc. 89 (10): 2342. doi :10.1021/ja00986a018.
- ^ abc Stein, Allan R.; Tencer, Michal; Moffatt, Elizabeth A.; Dawe, Robert; Sweet, James (1980). "Нелинейность корреляций Hammett .sigma..rho. для бензильных систем: параметры активации и их механистические последствия". J. Org. Chem. 45 (17): 3539–3540. doi :10.1021/jo01305a045.
- ^ Young, PR; Jencks, WP (1979). «Разделение эффектов полярных и резонансных заместителей в реакциях ацетофенонов с бисульфитом и бензилгалогенидов с нуклеофилами». J. Am. Chem. Soc. 101 (12): 3288. doi :10.1021/ja00506a025.
- ^ Болс, Микаэль; Лян, Сифу; Йенсен, Хенрик Х. (2002). «Экваториальные контраксиальные полярные заместители. Связь химической реакции со стереохимическими константами заместителей». J. Org. Chem. 67 (25): 8970–4. doi :10.1021/jo0205356. PMID 12467416.
- ^ Линдерберг, Б.; Свенссон, С.; Мальмквист, ПА; Базилье, Э.; Гелиус, У.; Зигбан, К. (1976). «Корреляция сдвигов ESCA и констант заместителей Гаммета в замещенных производных бензола». Chem. Phys. Lett. 40 (2): 175. Bibcode :1976CPL....40..175L. doi :10.1016/0009-2614(76)85053-1.
- ^ Takahata Y.; Chong DP (2005). «Оценка констант сигма Гаммета замещенных бензолов с помощью точного расчета сдвигов энергии связи остовных электронов с помощью функционала плотности». Международный журнал квантовой химии . 103 (5): 509–515. Bibcode : 2005IJQC..103..509T. doi : 10.1002/qua.20533.
Дальнейшее чтение
Общий
- Томас Х. Лоури и Кэтлин Шуллер Ричардсон, 1987, Механизм и теория в органической химии, 3-е изд., Нью-Йорк, штат Нью-Йорк, США: Harper & Row, ISBN 0060440848 , см. [2], доступ получен 20 июня 2015 г.
- Фрэнсис А. Кэри и Ричард Дж. Сандберг, 2006, «Название Advanced Organic Chemistry: Part A: Structure and Mechanisms», 4-е изд., Нью-Йорк, США: Springer Science & Business Media, ISBN 0306468565 , см. [3], по состоянию на 19 июня 2015 г.
- Майкл Б. Смит и Джерри Марч, 2007, «March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure», 6-е изд., Нью-Йорк, США: Wiley & Sons, ISBN 0470084944 , см. [4], доступ получен 19 июня 2015 г.
Теория
- Л. П. Хэмметт, 1970, Физическая органическая химия, 2-е изд., Нью-Йорк, США: McGraw-Hill.
- Джон Шортер, 1982, Корреляционный анализ органической реактивности, Чичестер, 1982.
- Отто Экснер, 1988, Корреляционный анализ химических данных, Нью-Йорк, США: Пленум.
Опросы дескрипторов
- Роберто Тодескини, Вивиана Консонни, Раймунд Маннхольд, Хьюго Кубиньи и Хендрик Тиммерман, 2008, «Вступление: Константы электронных заместителей (константы заместителей Хаммета, σ-электронные константы)», в Handbook of Molecular Descriptors, том 11 из Methods and Principles in Medicinal Chemistry (серия книг), стр. 144–157, Нью-Йорк, США: John Wiley & Sons, ISBN 3527613110 , см. [5], доступ получен 22 июня 2015 г.
- Н. Чепмен, 2012, Корреляционный анализ в химии: последние достижения, Нью-Йорк, США: Springer Science & Business, ISBN 1461588316 , см. [6], доступ получен 22 июня 2015 г.
История
- Робертс, Джон Д. (1996). «Начало физической органической химии в Соединенных Штатах» (PDF) . Bull. Hist. Chem. 19 : 48–56.
- Джон Шортер, 2000, «Предыстория уравнения Гаммета», Chem. Listy, 94 :210-214.
- Фрэнк Вестхаймер, 1997, «Луи Плэк Хэмметт, 1894—1987: Биографические мемуары», стр. 136–149, в Biographical Memoirs, Вашингтон, округ Колумбия, США: National Academies Press, см. [7], доступ получен 22 июня 2015 г.