1 42 многогранник

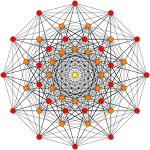4 21	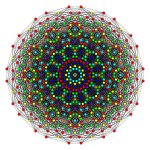1 42	2 41
Исправлено 4 21	Исправлено 1 42	Исправлено 2 41
Двукратное исправление 4 21	Триректификат 4 21
Ортогональные проекции в плоскости Коксетера E 6

В 8-мерной геометрии 1 ₄₂ представляет собой однородный 8- мерный многогранник , построенный в рамках симметрии группы E ₈ .

Его символ Коксетера — 1 ₄₂ , описывающий его бифуркационную диаграмму Коксетера-Дынкина с одним кольцом на конце последовательностей из 1 узла.

Выпрямленный 1 ₄₂ строится по точкам на средних ребрах 1 ₄₂ и совпадает с бивыпрямленным 2 ₄₁ и квадривыпрямленным 4 ₂₁ .

Эти многогранники являются частью семейства из 255 (2 ⁸  − 1) выпуклых однородных многогранников в 8 измерениях, состоящих из однородных граней многогранника и вершинных фигур , определяемых всеми непустыми комбинациями колец в этой диаграмме Коксетера-Дынкина :.

1 42
Тип	Однородный 8-многогранник
Семья	1 k2 многогранник
Символ Шлефли	{3,3 4,2 }
символ Коксетера	1 42
Диаграммы Коксетера
7-гранный	2400: 240 1 32 2160 1 41
6-гранный	106080: 6720 1 22 30240 1 31 69120 {3 5 }
5-гранный	725760: 60480 1 12 181440 1 21 483840 {3 4 }
4-х гранный	2298240: 241920 1 02 604800 1 11 1451520 {3 3 }
Клетки	3628800: 1209600 1 01 2419200 {3 2 }
Лица	2419200 {3}
Края	483840
Вершины	17280
Вершинная фигура	т 2 {3 6 }
Петри полигон	30-угольник
Группа Коксетера	Э 8 , [3 4,2,1 ]
Характеристики	выпуклый

1 ₄₂ состоит из 2400 граней: 240 многогранников 1 ₃₂ и 2160 7-демикубов ( 1 ₄₁ ). Его вершинная фигура — двойное выпрямление 7-симплекса .

Этот многогранник, наряду с полуоктерактом , может замостить 8-мерное пространство, представленное символом 1 ₅₂ , и диаграмму Коксетера-Дынкина:.

• Э. Л. Элте (1912) исключил этот многогранник из своего списка полуправильных многогранников, поскольку он имеет более двух типов 6-граней, но по его схеме наименования он будет называться V ₁₇₂₈₀ из-за его 17280 вершин. ^[1]
• Коксетер назвал его 1 ₄₂ из-за его бифурцирующей диаграммы Коксетера-Дынкина с одним кольцом на конце ветви с 1 узлом.
• Диакозитетраконт-дисхилиагектогексаконта-цеттон (аббревиатура bif ) - 240-2160 граненый полицеттон (Джонатан Бауэрс) ^[2]

17280 вершин можно определить как перестановки знаков и местоположений:

Все комбинации знаков (32): (280×32=8960 вершин)

(4, 2, 2, 2, 2, 0, 0, 0)

Половина комбинаций знаков (128): ((1+8+56)×128=8320 вершин)

(2, 2, 2, 2, 2, 2, 2, 2)

(5, 1, 1, 1, 1, 1, 1, 1)

(3, 3, 3, 1, 1, 1, 1, 1)

Длина ребра в этом наборе координат равна 2 √ 2 , а радиус многогранника равен 4 √ 2 .

Он создан с помощью конструкции Витхоффа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве.

Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина :.

Удаление узла на конце ветви длиной 2 оставляет 7-демикуб , 1 ₄₁ ,.

Удаление узла на конце ветви длиной 4 оставляет 1 ₃₂ ,.

Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это делает биректифицированный 7-симплекс , 0 ₄₂ ,.

Рассматривая матрицу конфигурации , количество элементов можно получить путем удаления зеркал и отношений порядков групп Кокстера . ^[3]

		Матрица конфигурации
Е 8		к -лицо	ф к	ф 0	ф 1	ф 2	ф 3		ф 4			ф 5			ф 6			ф 7		к -цифра	примечания
А 7		( )	ф 0	17280	56	420	280	560	70	280	420	56	168	168	28	56	28	8	8	2р{3 6 }	Э 8 /А 7 = 192*10!/8! = 17280
А 4 А 2 А 1		{ }	ф 1	2	483840	15	15	30	5	30	30	10	30	15	10	15	3	5	3	{3}x{3,3,3}	Е 8 /А 4 А 2 А 1 = 192*10!/5!/2/2 = 483840
А 3 А 2 А 1		{3}	ф 2	3	3	2419200	2	4	1	8	6	4	12	4	6	8	1	4	2	{3.3}в{ }	Е 8 /А 3 А 2 А 1 = 192*10!/4!/3!/2 = 2419200
А 3 А 3		1 10	ф 3	4	6	4	1209600	*	1	4	0	4	6	0	6	4	0	4	1	{3,3}в( )	Е 8 /А 3 А 3 = 192*10!/4!/4! = 1209600
А 3 А 2 А 1				4	6	4	*	2419200	0	2	3	1	6	3	3	6	1	3	2	{3}в{ }	Е 8 /А 3 А 2 А 1 = 192*10!/4!/3!/2 = 2419200
А 4 А 3		1 20	ф 4	5	10	10	5	0	241920	*	*	4	0	0	6	0	0	4	0	{3,3}	Е 8 /А 4 А 3 = 192*10!/4!/4! = 241920
Д 4 А 2		1 11		8	24	32	8	8	*	604800	*	1	3	0	3	3	0	3	1	{3}в( )	Э 8 /Д 4 А 2 = 192*10!/8/4!/3! = 604800
А 4 А 1 А 1		1 20		5	10	10	0	5	*	*	1451520	0	2	2	1	4	1	2	2	{ }v{ }	Е 8 /А 4 А 1 А 1 = 192*10!/5!/2/2 = 1451520
Д 5 А 2		1 21	ф 5	16	80	160	80	40	16	10	0	60480	*	*	3	0	0	3	0	{3}	Э 8 /Д 5 А 2 = 192*10!/16/5!/3! = 40480
Д 5 А 1				16	80	160	40	80	0	10	16	*	181440	*	1	2	0	2	1	{ }в( )	Э 8 /Д 5 А 1 = 192*10!/16/5!/2 = 181440
А 5 А 1		1 30		6	15	20	0	15	0	0	6	*	*	483840	0	2	1	1	2		Е 8 /А 5 А 1 = 192*10!/6!/2 = 483840
Э 6 А 1		1 22	ф 6	72	720	2160	1080	1080	216	270	216	27	27	0	6720	*	*	2	0	{ }	Е 8 /Е 6 А 1 = 192*10!/72/6!/2 = 6720
Д 6		1 31		32	240	640	160	480	0	60	192	0	12	32	*	30240	*	1	1		Э 8 /Д 6 = 192*10!/32/6! = 30240
А 6 А 1		1 40		7	21	35	0	35	0	0	21	0	0	7	*	*	69120	0	2		Е 8 /А 6 А 1 = 192*10!/7!/2 = 69120
Е 7		1 32	ф 7	576	10080	40320	20160	30240	4032	7560	12096	756	1512	2016	56	126	0	240	*	( )	Е 8 /Е 7 = 192*10!/72/8! = 240
Д 7		1 41		64	672	2240	560	2240	0	280	1344	0	84	448	0	14	64	*	2160		Э 8 /Д 7 = 192*10!/64/7! = 2160

Е8 [30]	Е7 [18]	Е6 [12]
(1)	(1,3,6)	(8,16,24,32,48,64,96)
[20]	[24]	[6]
		(1,2,3,4,5,6,7,8,10,11,12,14,16,18,19,20)

Ортографические проекции показаны для подсимметрий E ₈ : плоскостей Кокстера E ₇ , E ₆ , B ₈ , B _{7 , B 6} , B ₅ , B ₄ , B ₃ , B ₂ , A ₇ и A ₅ , а также еще двух плоскостей симметрии порядков 20 и 24. Вершины показаны в виде окружностей, раскрашенных в соответствии с порядком их перекрытия в каждой проективной плоскости.

Д3 / В2 / А3 [4]	Д4 / В3 / А2 [6]	Д5 / В4 [8]
(32 160 192 240 480 512 832 960)	(72,216,432,720,864,1080)	(8,16,24,32,48,64,96)
Д6 / В5 / А4 [10]	Д7 / Б6 [12]	Д8 / В7 / А6 [14]
Б8 [16/2]	А5 [6]	А7 [8]

1 k2 фигур в n измерениях
Космос	Конечный						Евклидов	Гиперболический
н	3	4	5	6	7	8	9	10
Группа Коксетера	Э 3 =А 2 А 1	Э 4 =А 4	Э 5 =Д 5	Е 6	Е 7	Е 8	Э 9 = = Э 8 +${\displaystyle {\tilde {E}}_{8}}$	Е 10 = = Е 8 ++${\displaystyle {\bar {T}}_{8}}$
Диаграмма Коксетера
Симметрия (порядок)	[3 −1,2,1 ]	[3 0,2,1 ]	[3 1,2,1 ]	[[3 2,2,1 ]]	[3 3,2,1 ]	[3 4,2,1 ]	[3 5,2,1 ]	[3 6,2,1 ]
Заказ	12	120	1,920	103,680	2,903,040	696,729,600	∞
График							-	-
Имя	1 −1,2	1 02	1 12	1 22	1 32	142	1 52	1 62

Исправлено 1 42
Тип	Однородный 8-многогранник
Символ Шлефли	т 1 {3,3 4,2 }
символ Коксетера	0 421
Диаграммы Коксетера
7-гранный	19680
6-гранный	382560
5-гранный	2661120
4-х гранный	9072000
Клетки	16934400
Лица	16934400
Края	7257600
Вершины	483840
Вершинная фигура	{3,3,3}×{3}×{}
Группа Коксетера	Э 8 , [3 4,2,1 ]
Характеристики	выпуклый

Выпрямленный 1 ₄₂ назван так потому, что является выпрямлением многогранника 1 ₄₂ с вершинами, расположенными на средних ребрах 1 _42. Его также можно назвать многогранником 0 ₄₂₁ с кольцом в центре трех ветвей длиной 4, 2 и 1.

• 0 ₄₂₁ многогранник
• Двуспрямленный многогранник 2 ₄₁
• Квадриректифицированный 4 ₂₁ многогранник
• Очищенный диакозитетраконт-дисхилиагектогексаконта-цеттон как очищенный 240-2160 граненый полизеттон (сокращенно баффи ) (Джонатан Бауэрс) ^[4]

Он создан с помощью конструкции Витхоффа на основе набора из 8 гиперплоских зеркал в 8-мерном пространстве.

Информацию о фасетах можно извлечь из диаграммы Коксетера-Дынкина :.

Удаление узла на конце ветви длиной 1 оставляет биспрямленный 7-симплекс ,

Удаление узла на конце ветви длины 2 оставляет двояковыпрямленный 7-куб ,.

Удаление узла на конце ветви длиной 3 оставляет выпрямленное 1 ₃₂ ,.

Вершинная фигура определяется путем удаления окольцованного узла и окольцования соседнего узла. Это дает 5-клеточную - треугольную дуопризму призму,.

Рассматривая матрицу конфигурации , количество элементов можно получить путем удаления зеркал и отношений порядков групп Кокстера . ^[3]

		Матрица конфигурации
Е 8		к -лицо	ф к	ф 0	ф 1	ф 2			ф 3					ф 4						ф 5						ф 6					ф 7			к -цифра
А 4 А 2 А 1		( )	ф 0	483840	30	30	15	60	10	15	60	30	60	5	20	30	60	30	30	10	20	30	30	15	6	10	10	15	6	3	5	2	3	{3,3,3}х{3,3}х{}
А 3 А 1 А 1		{ }	ф 1	2	7257600	2	1	4	1	2	8	4	6	1	4	8	12	6	4	4	6	12	8	4	1	6	4	8	2	1	4	1	2
А 3 А 2		{3}	ф 2	3	3	4838400	*	*	1	1	4	0	0	1	4	4	6	0	0	4	6	6	4	0	0	6	4	4	1	0	4	1	1
А 3 А 2 А 1				3	3	*	2419200	*	0	2	0	4	0	1	0	8	0	6	0	4	0	12	0	4	0	6	0	8	0	1	4	0	2
А 2 А 2 А 1				3	3	*	*	9676800	0	0	2	1	3	0	1	2	6	3	3	1	3	6	6	3	1	3	3	6	2	1	3	1	2
А 3 А 3		0 200	ф 3	4	6	4	0	0	1209600	*	*	*	*	1	4	0	0	0	0	4	6	0	0	0	0	6	4	0	0	0	4	1	0
		0 110		6	12	4	4	0	*	1209600	*	*	*	1	0	4	0	0	0	4	0	6	0	0	0	6	0	4	0	0	4	0	1
А 3 А 2				6	12	4	0	4	*	*	4838400	*	*	0	1	1	3	0	0	1	3	3	3	0	0	3	3	3	1	0	3	1	1
А 3 А 2 А 1				6	12	0	4	4	*	*	*	2419200	*	0	0	2	0	3	0	1	0	6	0	3	0	3	0	6	0	1	3	0	2
А 3 А 1 А 1		0 200		4	6	0	0	4	*	*	*	*	7257600	0	0	0	2	1	2	0	1	2	4	2	1	1	2	4	2	1	2	1	2
А 4 А 3		0 210	ф 4	10	30	20	10	0	5	5	0	0	0	241920	*	*	*	*	*	4	0	0	0	0	0	6	0	0	0	0	4	0	0
А 4 А 2				10	30	20	0	10	5	0	5	0	0	*	967680	*	*	*	*	1	3	0	0	0	0	3	3	0	0	0	3	1	0
Д 4 А 2		0 111		24	96	32	32	32	0	8	8	8	0	*	*	604800	*	*	*	1	0	3	0	0	0	3	0	3	0	0	3	0	1
А 4 А 1		0 210		10	30	10	0	20	0	0	5	0	5	*	*	*	2903040	*	*	0	1	1	2	0	0	1	2	2	1	0	2	1	1
А 4 А 1 А 1				10	30	0	10	20	0	0	0	5	5	*	*	*	*	1451520	*	0	0	2	0	2	0	1	0	4	0	1	2	0	2
А 4 А 1		0 300		5	10	0	0	10	0	0	0	0	5	*	*	*	*	*	2903040	0	0	0	2	1	1	0	1	2	2	1	1	1	2
Д 5 А 2		0 211	ф 5	80	480	320	160	160	80	80	80	40	0	16	16	10	0	0	0	60480	*	*	*	*	*	3	0	0	0	0	3	0	0	{3}
А 5 А 1		0 220		20	90	60	0	60	15	0	30	0	15	0	6	0	6	0	0	*	483840	*	*	*	*	1	2	0	0	0	2	1	0	{ }v()
Д 5 А 1		0 211		80	480	160	160	320	0	40	80	80	80	0	0	10	16	16	0	*	*	181440	*	*	*	1	0	2	0	0	2	0	1
А 5		0 310		15	60	20	0	60	0	0	15	0	30	0	0	0	6	0	6	*	*	*	967680	*	*	0	1	1	1	0	1	1	1	( )в( )в()
А 5 А 1				15	60	0	20	60	0	0	0	15	30	0	0	0	0	6	6	*	*	*	*	483840	*	0	0	2	0	1	1	0	2	{ }v()
		0 400		6	15	0	0	20	0	0	0	0	15	0	0	0	0	0	6	*	*	*	*	*	483840	0	0	0	2	1	0	1	2
Э 6 А 1		0 221	ф 6	720	6480	4320	2160	4320	1080	1080	2160	1080	1080	216	432	270	432	216	0	27	72	27	0	0	0	6720	*	*	*	*	2	0	0	{ }
А 6		0 320		35	210	140	0	210	35	0	105	0	105	0	21	0	42	0	21	0	7	0	7	0	0	*	138240	*	*	*	1	1	0
Д 6		0 311		240	1920	640	640	1920	0	160	480	480	960	0	0	60	192	192	192	0	0	12	32	32	0	*	*	30240	*	*	1	0	1
А 6		0 410		21	105	35	0	140	0	0	35	0	105	0	0	0	21	0	42	0	0	0	7	0	7	*	*	*	138240	*	0	1	1
А 6 А 1				21	105	0	35	140	0	0	0	35	105	0	0	0	0	21	42	0	0	0	0	7	7	*	*	*	*	69120	0	0	2
Е 7		0 321	ф 7	10080	120960	80640	40320	120960	20160	20160	60480	30240	60480	4032	12096	7560	24192	12096	12096	756	4032	1512	4032	2016	0	56	576	126	0	0	240	*	*	( )
А 7		0 420		56	420	280	0	560	70	0	280	0	420	0	56	0	168	0	168	0	28	0	56	0	28	0	8	0	8	0	*	17280	*
Д 7		0 411		672	6720	2240	2240	8960	0	560	2240	2240	6720	0	0	280	1344	1344	2688	0	0	84	448	448	448	0	0	14	64	64	*	*	2160

Ортографические проекции показаны для подсимметрий плоскостей Коксетера B ₆ , B ₅ , B ₄ , B ₃ , B ₂ , A ₇ и A ₅ . Вершины показаны в виде кругов, окрашенных в порядке их перекрытия в каждой проективной плоскости.

(Плоскости для E ₈ : E ₇ , E ₆ , B ₈ , B ₇ , [24] не показаны, так как они слишком велики для отображения.)

Д3 / В2 / А3 [4]	Д4 / В3 / А2 [6]	Д5 / В4 [8]
Д6 / В5 / А4 [10]	Д7 / Б6 [12]	[6]
А5 [6]	А7 [8]	[20]

• Список многогранников E8

• HSM Coxeter , Правильные многогранники , 3-е издание, Довер, Нью-Йорк, 1973
• Калейдоскопы: Избранные сочинения HSM Coxeter , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 Калейдоскопы: Избранные сочинения HSM Coxeter | Wiley 
  • (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
• Клитцинг, Ричард. «8D Uniform polyzetta».o3o3o3x *c3o3o3o3o - биф, o3o3o3x *c3o3o3o3o - баффи