Функтор

В математике , в частности в теории категорий , функтор — это отображение между категориями . Функторы впервые были рассмотрены в алгебраической топологии , где алгебраические объекты (такие как фундаментальная группа ) связаны с топологическими пространствами , а отображения между этими алгебраическими объектами связаны с непрерывными отображениями между пространствами. В настоящее время функторы используются в современной математике для связи различных категорий. Таким образом, функторы важны во всех областях математики, к которым применяется теория категорий .

Слова «категория» и «функтор» были заимствованы математиками у философов Аристотеля и Рудольфа Карнапа соответственно. ^[1] Последний использовал «функтор» в лингвистическом контексте; ^[2] см. слово «функция» .

Эта статья может быть слишком технической для понимания большинства читателей . Пожалуйста, помогите улучшить ее, чтобы сделать ее понятной для неспециалистов , не удаляя технические детали. ( Ноябрь 2023 ) ( Узнайте, как и когда удалить это сообщение )

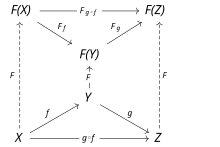
Пусть C и D — категории . Функтор F из C в D — это отображение, которое ^[3]

• связывает каждый объект в C с объектом в D ,${\displaystyle X}$${\displaystyle F(X)}$
• связывает каждый морфизм в C с морфизмом в D таким образом, что выполняются следующие два условия:${\displaystyle f\двоеточие от X до Y}$${\displaystyle F(f)\двоеточие F(X)\to F(Y)}$
  • ${\displaystyle F(\mathrm {id} _{X})=\mathrm {id} _{F(X)}\,\!}$для каждого объекта в C ,${\displaystyle X}$
  • ${\displaystyle F(г\circ f)=F(г)\circ F(f)}$для всех морфизмов и в C.${\displaystyle f\двоеточие от X\до Y\,\!}$${\displaystyle g\colon Y\to Z}$

То есть функторы должны сохранять тождественные морфизмы и композицию морфизмов.

В математике существует множество конструкций, которые были бы функторами, если бы не тот факт, что они «переворачивают морфизмы» и «обратную композицию». Затем мы определяем контравариантный функтор F из C в D как отображение, которое

• связывает каждый объект в C с объектом в D ,${\displaystyle X}$${\displaystyle F(X)}$
• связывает каждый морфизм в C с морфизмом в D таким образом, что выполняются следующие два условия:${\displaystyle f\colon X\to Y}$${\displaystyle F(f)\colon F(Y)\to F(X)}$
  • ${\displaystyle F(\mathrm {id} _{X})=\mathrm {id} _{F(X)}\,\!}$для каждого объекта в C ,${\displaystyle X}$
  • ${\displaystyle F(g\circ f)=F(f)\circ F(g)}$для всех морфизмов и в C.${\displaystyle f\colon X\to Y}$${\displaystyle g\colon Y\to Z}$

Дисперсия функтора (композитная) ^[4]

• Композиция двух функторов одинаковой дисперсии:
  • ${\displaystyle \mathrm {Covariant} \circ \mathrm {Covariant} \to \mathrm {Covariant} }$
  • ${\displaystyle \mathrm {Contravariant} \circ \mathrm {Contravariant} \to \mathrm {Covariant} }$
• Композиция двух функторов с противоположной дисперсией:
  • ${\displaystyle \mathrm {Covariant} \circ \mathrm {Contravariant} \to \mathrm {Contravariant} }$
  • ${\displaystyle \mathrm {Contravariant} \circ \mathrm {Covariant} \to \mathrm {Contravariant} }$

Обратите внимание, что контравариантные функторы меняют направление композиции на противоположное.

Обычные функторы также называются ковариантными функторами , чтобы отличать их от контравариантных. Обратите внимание, что контравариантный функтор можно также определить как ковариантный функтор на противоположной категории . ^[5] Некоторые авторы предпочитают записывать все выражения ковариантно. То есть, вместо того, чтобы говорить является контравариантным функтором, они просто пишут (или иногда ) и называют его функтором.${\displaystyle C^{\mathrm {op} }}$${\displaystyle F\colon C\to D}$${\displaystyle F\colon C^{\mathrm {op} }\to D}$${\displaystyle F\colon C\to D^{\mathrm {op} }}$

Контравариантные функторы также иногда называют кофункторами . ^[6]

Существует соглашение, которое ссылается на «векторы» — т. е. векторные поля , элементы пространства сечений касательного расслоения — как на «контравариантные», а на «ковекторы» — т. е. 1-формы , элементы пространства сечений кокасательного расслоения — как на «ковариантные». Эта терминология берет свое начало в физике, и ее обоснование связано с положением индексов («вверху» и «внизу») в выражениях, таких как для или для В этом формализме наблюдается, что символ преобразования координат (представляющий матрицу ) действует на «координаты ковектора» «таким же образом», как на базисные векторы: — тогда как на «координаты вектора» он действует «обратным образом» (но «таким же образом», как на базисные ковекторы: ). Эта терминология противоречит той, которая используется в теории категорий, поскольку именно ковекторы имеют обратные пути в общем случае и, таким образом, контравариантны , тогда как векторы в общем случае ковариантны, поскольку их можно продвинуть вперед . См. также Ковариантность и контравариантность векторов .${\displaystyle \Gamma (TM)}$ ${\displaystyle TM}$${\displaystyle \Gamma {\mathord {\left(T^{*}M\right)}}}$ ${\displaystyle T^{*}M}$${\displaystyle {x'}^{\,i}=\Lambda _{j}^{i}x^{j}}$${\displaystyle \mathbf {x} '={\boldsymbol {\Lambda }}\mathbf {x} }$${\displaystyle \omega '_{i}=\Lambda _{i}^{j}\omega _{j}}$${\displaystyle {\boldsymbol {\omega }}'={\boldsymbol {\omega }}{\boldsymbol {\Lambda }}^{\textsf {T}}.}$${\displaystyle \Lambda _{i}^{j}}$${\displaystyle {\boldsymbol {\Lambda }}^{\textsf {T}}}$${\displaystyle \mathbf {e} _{i}=\Lambda _{i}^{j}\mathbf {e} _{j}}$${\displaystyle \mathbf {e} ^{i}=\Lambda _{j}^{i}\mathbf {e} ^{j}}$

Каждый функтор индуцирует противоположный функтор , где и являются противоположными категориями к и . ^[7] По определению, отображает объекты и морфизмы таким же образом, как и . Поскольку не совпадает с как категория, и аналогично для , отличается от . Например, при композиции с следует использовать либо , либо . Обратите внимание, что, следуя свойству противоположной категории , .${\displaystyle F\colon C\to D}$ ${\displaystyle F^{\mathrm {op} }\colon C^{\mathrm {op} }\to D^{\mathrm {op} }}$${\displaystyle C^{\mathrm {op} }}$${\displaystyle D^{\mathrm {op} }}$${\displaystyle C}$${\displaystyle D}$${\displaystyle F^{\mathrm {op} }}$${\displaystyle F}$${\displaystyle C^{\mathrm {op} }}$${\displaystyle C}$${\displaystyle D}$${\displaystyle F^{\mathrm {op} }}$${\displaystyle F}$${\displaystyle F\colon C_{0}\to C_{1}}$${\displaystyle G\colon C_{1}^{\mathrm {op} }\to C_{2}}$${\displaystyle G\circ F^{\mathrm {op} }}$${\displaystyle G^{\mathrm {op} }\circ F}$${\displaystyle \left(F^{\mathrm {op} }\right)^{\mathrm {op} }=F}$

Бифунктор (также известный как бинарный функтор ) — это функтор, областью определения которого является категория произведения . Например, функтор Hom имеет тип C ^op × C → Set . Его можно рассматривать как функтор от двух аргументов; он контравариантен в одном аргументе и ковариантен в другом.

Мультифунктор — это обобщение концепции функтора на n переменных. Так, например, бифунктор — это мультифунктор с n = 2 .

Два важных следствия аксиом функтора :

• F преобразует каждую коммутативную диаграмму в C в коммутативную диаграмму в D ;
• если f является изоморфизмом в C , то F ( f ) является изоморфизмом в D.

Можно составлять функторы, т.е. если F — функтор из A в B , а G — функтор из B в C , то можно образовать составной функтор G ∘ F из A в C. Композиция функторов ассоциативна, если определена. Тождество композиции функторов — это тождественный функтор. Это показывает, что функторы можно рассматривать как морфизмы в категориях категорий, например, в категории малых категорий .

Малая категория с одним объектом — это то же самое, что и моноид : морфизмы категории с одним объектом можно рассматривать как элементы моноида, а композиция в категории рассматривается как операция моноида. Функторы между категориями с одним объектом соответствуют гомоморфизмам моноида . Так что в некотором смысле функторы между произвольными категориями являются своего рода обобщением гомоморфизмов моноида на категории с более чем одним объектом.

Диаграмма

Для категорий C и J диаграмма типа J в C является ковариантным функтором .${\displaystyle D\colon J\to C}$

(Категория теоретическая) предпучок

Для категорий C и J J -предпучок на C является контравариантным функтором .${\displaystyle D\colon C\to J}$

В частном случае, когда J — это Set , категория множеств и функций, D называется предпучком на C.

Предпучки (над топологическим пространством)

Если X — топологическое пространство , то открытые множества в X образуют частично упорядоченное множество Open( X ) при включении. Как и каждое частично упорядоченное множество, Open( X ) образует малую категорию, добавляя одну стрелку U → V тогда и только тогда, когда . Контравариантные функторы на Open( X ) называются предпучками на X . Например, назначая каждому открытому множеству U ассоциативную алгебру действительнозначных непрерывных функций на U , получаем предпучок алгебр на X .${\displaystyle U\subseteq V}$

Константный функтор

Функтор C → D , который отображает каждый объект C в фиксированный объект X в D , а каждый морфизм в C в тождественный морфизм на X. Такой функтор называется константным или селекционным функтором.

Эндофунктор

Функтор, который отображает категорию в эту же категорию; например, полиномиальный функтор .

Функтор тождественности

В категории C , обозначаемой как 1 _C или id _C , отображает объект в себя и морфизм в себя. Функтор тождества является эндофунктором.

Диагональный функтор

Диагональный функтор определяется как функтор из D в категорию функторов D ^C , который переводит каждый объект в D в постоянный функтор в этом объекте.

Предельный функтор

Для фиксированной индексной категории J , если каждый функтор J → C имеет предел (например, если C является полным), то предельный функтор C ^J → C назначает каждому функтору его предел. Существование этого функтора можно доказать, поняв, что он является правым сопряженным к диагональному функтору, и применив теорему Фрейда о сопряженном функторе . Для этого требуется подходящая версия аксиомы выбора . Аналогичные замечания применимы к функтору копредела (который назначает каждому функтору его копредел и является ковариантным).

Функтор множеств мощности

Функтор множества мощности P  : Set → Set отображает каждое множество в его множество мощности и каждую функцию в отображение, которое отправляет в его образ . Можно также рассмотреть контравариантный функтор множества мощности , который отправляет в отображение, которое отправляет в его обратный образ${\displaystyle f\colon X\to Y}$${\displaystyle U\in {\mathcal {P}}(X)}$${\displaystyle f(U)\in {\mathcal {P}}(Y)}$${\displaystyle f\colon X\to Y}$${\displaystyle V\subseteq Y}$ ${\displaystyle f^{-1}(V)\subseteq X.}$

Например, если то . Предположим и . Тогда — функция, которая отправляет любое подмножество в его образ , что в данном случае означает , где обозначает отображение под , поэтому это можно также записать как . Для других значений Обратите внимание, что следовательно генерирует тривиальную топологию на . Также обратите внимание, что хотя функция в этом примере отображается в множество мощности , в общем случае это не обязательно так.${\displaystyle X=\{0,1\}}$${\displaystyle F(X)={\mathcal {P}}(X)=\{\{\},\{0\},\{1\},X\}}$${\displaystyle f(0)=\{\}}$${\displaystyle f(1)=X}$${\displaystyle F(f)}$${\displaystyle U}$${\displaystyle X}$${\displaystyle f(U)}$${\displaystyle \{\}\mapsto f(\{\})=\{\}}$${\displaystyle \mapsto }$${\displaystyle F(f)}$${\displaystyle (F(f))(\{\})=\{\}}$${\displaystyle \{0\}\mapsto f(\{0\})=\{f(0)\}=\{\{\}\},\ }$ ${\displaystyle \{1\}\mapsto f(\{1\})=\{f(1)\}=\{X\},\ }$ ${\displaystyle \{0,1\}\mapsto f(\{0,1\})=\{f(0),f(1)\}=\{\{\},X\}.}$${\displaystyle f(\{0,1\})}$${\displaystyle X}$${\displaystyle f}$${\displaystyle X}$

Двойственное векторное пространство

Отображение, которое каждому векторному пространству сопоставляет его двойственное пространство , а каждому линейному отображению — его двойственное или транспонированное пространство, является контравариантным функтором из категории всех векторных пространств над фиксированным полем в себя.

Основная группа

Рассмотрим категорию точечных топологических пространств , т.е. топологических пространств с выделенными точками. Объектами являются пары ( X , x0 ) , где X — топологическое пространство, а x0 — _точка в X. Морфизм из ( X , x0 ) _в ( Y , _y0 ) задается непрерывным отображением f  : X → Y с _f ( x0 ₎ = y0 _.

Для каждого топологического пространства X с выделенной точкой x 0 можно определить фундаментальную группу с базой в x 0 , обозначаемую π 1 ( X , x 0 ) . Это группа гомотопических классов петель с _базой в x 0 , _с групповой операцией _{конкатенации} . Если f : _X → Y — морфизм точечных пространств _, то каждая  петля в X с базовой точкой x 0 может быть _{скомпонована} с f для получения петли в Y с базовой точкой y ₀ . Эта операция совместима с отношением гомотопической эквивалентности и композицией петель, и мы получаем групповой гомоморфизм из π( X , x ₀ ) в π( Y , y ₀ ) . Таким образом, мы получаем функтор из категории точечных топологических пространств в категорию групп .

В категории топологических пространств (без выделенной точки) рассматриваются гомотопические классы общих кривых, но они не могут быть составлены, если они не имеют общей конечной точки. Таким образом, вместо фундаментальной группы мы имеем фундаментальный группоид , и эта конструкция является функториальной.

Алгебра непрерывных функций

Контравариантный функтор из категории топологических пространств (с непрерывными отображениями в качестве морфизмов) в категорию действительных ассоциативных алгебр задается путем присвоения каждому топологическому пространству X алгебры C( X ) всех действительнозначных непрерывных функций на этом пространстве. Каждое непрерывное отображение f  : X → Y индуцирует гомоморфизм алгебр C( f ) : C( Y ) → C( X ) по правилу C( f )( φ ) = φ ∘ f для любого φ из C( Y ).

Касательные и кокасательные расслоения

Отображение, которое переводит каждое дифференцируемое многообразие в его касательное расслоение , а каждое гладкое отображение в его производную, является ковариантным функтором из категории дифференцируемых многообразий в категорию векторных расслоений .

Выполнение этих построений поточечно дает касательное пространство , ковариантный функтор из категории точечных дифференцируемых многообразий в категорию действительных векторных пространств. Аналогично, кокасательное пространство является контравариантным функтором, по сути композицией касательного пространства с дуальным пространством выше.

Групповые действия/представления

Каждая группа G может рассматриваться как категория с единственным объектом, морфизмы которого являются элементами G . Тогда функтор из G в Set есть не что иное, как групповое действие G на определенном множестве, т. е. G -множестве. Аналогично, функтор из G в категорию векторных пространств , Vect _K , есть линейное представление G . В общем случае функтор G → C можно рассматривать как «действие» G на объект в категории C . Если C — группа, то это действие есть групповой гомоморфизм.

Алгебры Ли

Сопоставление каждой действительной (комплексной) группы Ли ее действительной (комплексной) алгебры Ли определяет функтор.

Тензорные продукты

Если C обозначает категорию векторных пространств над фиксированным полем с линейными отображениями в качестве морфизмов, то тензорное произведение определяет функтор C × C → C , который ковариантен по обоим аргументам. ^[8]${\displaystyle V\otimes W}$

Забывчивые функторы

Функтор U  : Grp → Set , который отображает группу в ее базовое множество, а гомоморфизм группы в ее базовую функцию множеств, является функтором. ^[9] Такие функторы, которые «забывают» некоторую структуру, называются забывающими функторами . Другим примером является функтор Rng → Ab , который отображает кольцо в его базовую аддитивную абелеву группу . Морфизмы в Rng ( гомоморфизмы колец ) становятся морфизмами в Ab (гомоморфизмы абелевых групп).

Свободные функторы

В противоположном направлении забывчивым функторам идут свободные функторы. Свободный функтор F  : Set → Grp отправляет каждое множество X в свободную группу, порожденную X . Функции отображаются в групповые гомоморфизмы между свободными группами. Свободные конструкции существуют для многих категорий, основанных на структурированных множествах. См. свободный объект .

Группы гомоморфизмов

Каждой паре A , B абелевых групп можно сопоставить абелеву группу Hom( A , B ), состоящую из всех групповых гомоморфизмов из A в B . Это функтор, который контравариантен по первому аргументу и ковариантен по второму, т.е. это функтор Ab ^op × Ab → Ab (где Ab обозначает категорию абелевых групп с групповыми гомоморфизмами). Если f  : A ₁ → A ₂ и g  : B ₁ → B ₂ являются морфизмами в Ab , то групповой гомоморфизм Hom( f , g ) : Hom( A ₂ , B ₁ ) → Hom( A ₁ , B ₂ ) задается формулой φ ↦ g ∘ φ ∘ f . См. Hom functor .

Представимые функторы

Мы можем обобщить предыдущий пример на любую категорию C. Каждой паре X , Y объектов в C можно сопоставить множество Hom( X , Y ) морфизмов из X в Y . Это определяет функтор в Set , который контравариантен по первому аргументу и ковариантен по второму, т.е. это функтор C ^op × C → Set . Если f  : X ₁ → X ₂ и g  : Y ₁ → Y ₂ являются морфизмами в C , то отображение Hom( f , g ) : Hom( X ₂ , Y ₁ ) → Hom( X ₁ , Y ₂ ) задается как φ ↦ g ∘ φ ∘ f .

Такие функторы называются представимыми функторами . Важной целью во многих ситуациях является определение того, представим ли данный функтор.

Пусть C и D — категории. Совокупность всех функторов от C до D образует объекты категории: категорию функторов . Морфизмы в этой категории — это естественные преобразования между функторами.

Функторы часто определяются универсальными свойствами ; примерами являются тензорное произведение , прямая сумма и прямое произведение групп или векторных пространств, построение свободных групп и модулей, прямые и обратные пределы. Понятия предела и копредела обобщают несколько из вышеперечисленных.

Универсальные конструкции часто приводят к появлению пар сопряженных функторов .

Функторы иногда появляются в функциональном программировании . Например, язык программирования Haskell имеет класс Functor , где fmap— политипная функция, используемая для отображения функций ( морфизмов на Hask , категории типов Haskell) ^[10] между существующими типами в функции между некоторыми новыми типами. ^[11]

• Анафунктор
• Профунктор
• Категория функторов
• Расширение Кан
• Псевдофунктор

• Якобсон, Натан (2009), Основы алгебры , т. 2 (2-е изд.), Дувр, ISBN 978-0-486-47187-7.
• Симмонс, Гарольд (2011), «Функторы и естественные преобразования», Введение в теорию категорий, стр.  72–107 , doi :10.1017/CBO9780511863226.004, ISBN 978-1-107-01087-1

Найдите слово «функтор» в Викисловаре, бесплатном словаре.

• «Функтор», Энциклопедия математики , EMS Press , 2001 [1994]
• см. функтор в n Lab и обсуждаемые там вариации, а также ссылки на них.
• Андре Жойал , CatLab, вики-проект, посвященный изложению категориальной математики
• Хиллман, Крис (2001). "A Categorical Primer". CiteSeerX  10.1.1.24.3264 . Архивировано из оригинала 1997-05-03.
• J. Adamek, H. Herrlich, G. Stecker, Абстрактные и конкретные категории — Радость кошек Архивировано 21.04.2015 на Wayback Machine
• Стэнфордская энциклопедия философии : «Теория категорий» — Жан-Пьер Марки. Обширная библиография.
• Список научных конференций по теории категорий
• Баез, Джон, 1996, «Сказка об n-категориях». Неформальное введение в категории высшего порядка.
• WildCats — пакет теории категорий для Mathematica . Манипулирование и визуализация объектов, морфизмов , категорий, функторов, естественных преобразований , универсальных свойств .
• The catsters — канал на YouTube о теории категорий.
• Видеоархив записанных докладов по категориям, логике и основам физики.
• Интерактивная веб-страница, генерирующая примеры категориальных конструкций в категории конечных множеств.