Расширение Кан

Расширения Кана являются универсальными конструкциями в теории категорий , разделе математики . Они тесно связаны с присоединенными элементами , но также связаны с пределами и концами . Они названы в честь Дэниела М. Кана , который построил некоторые расширения (Кан) с использованием пределов в 1960 году.

Раннее использование (то, что сейчас известно как) расширения Кана было в 1956 году в гомологической алгебре для вычисления производных функторов .

В книге «Категории для работающего математика» Сондерс Маклейн озаглавил раздел «Все концепции являются расширениями Кана» и продолжил, написав, что

Понятие расширений Кана включает в себя все другие фундаментальные концепции теории категорий.

Расширения Кана обобщают понятие расширения функции, определенной на подмножестве, до функции, определенной на всем множестве. Определение, что неудивительно, находится на высоком уровне абстракции. При специализации на частично упорядоченных множествах оно становится относительно знакомым типом вопроса по ограниченной оптимизации .

Расширение Кана исходит из данных трех категорий

${\displaystyle \mathbf {A},\mathbf {B},\mathbf {C} }$

и два функтора

${\displaystyle X:\mathbf {A} \to \mathbf {C} ,F:\mathbf {A} \to \mathbf {B} }$,

и существует в двух вариантах: «левое» расширение Кан и «правое» расширение Кан вдоль .${\displaystyle X}$${\displaystyle F}$

Абстрактно, функтор дает пулбэк-карту . Когда они существуют, левые и правые адъюнкты, примененные к, дают левые и правые расширения kan. Расписывая определение адъюнктов, мы получаем следующие определения;${\displaystyle F}$${\displaystyle F^{*}:[B,C]\to [A,C]}$${\displaystyle F^{*}}$${\displaystyle X}$

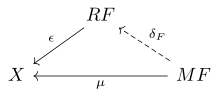
Правильное расширение Кана сводится к нахождению пунктирной стрелки и естественного преобразования на следующей диаграмме:${\displaystyle \epsilon}$

Формально, правое расширение Кана вдоль${\displaystyle X}$${\displaystyle F}$ состоит из функтора и естественного преобразования , которое коуниверсально относительно спецификации, в том смысле, что для любого функтора и естественного преобразования определяется единственное естественное преобразование, которое вписывается в коммутативную диаграмму:${\displaystyle R:\mathbf {B} \to \mathbf {C} }$${\displaystyle \epsilon :RF\to X}$${\displaystyle M:\mathbf {B} \to \mathbf {C} }$${\displaystyle \mu :MF\to X}$${\displaystyle \delta :M\to R}$

где есть естественное преобразование с для любого объекта${\displaystyle \delta _{F}}$${\displaystyle \delta _{F}(a)=\delta (Fa):MF(a)\to RF(a)}$ ${\displaystyle а}$${\displaystyle \mathbf {A} .}$

Функтор R часто записывается как .${\displaystyle \operatorname {Ran} _{F}X}$

Как и в случае с другими универсальными конструкциями в теории категорий , «левая» версия расширения Кана является дуальной по отношению к «правой» и получается путем замены всех категорий их противоположностями .

Эффект этого в описании выше заключается лишь в том, что направление естественных преобразований меняется на противоположное.

(Напомним, что естественное преобразование между функторами состоит в наличии стрелки для каждого объекта , удовлетворяющей свойству «естественности». Когда мы переходим к противоположным категориям, источник и цель меняются местами, заставляя действовать в противоположном направлении).${\displaystyle \тау}$${\displaystyle F,G:\mathbf {C} \to \mathbf {D} }$ ${\displaystyle \tau (a):F(a)\to G(a)}$${\displaystyle а}$${\displaystyle \mathbf {C} }$${\displaystyle \тау (а)}$${\displaystyle \тау}$

Это приводит к альтернативному описанию: левое расширение Кана вдоль${\displaystyle X}$${\displaystyle F}$ состоит из функтора и естественного преобразования , которые являются универсальными относительно этой спецификации, в том смысле, что для любого другого функтора и естественного преобразования существует единственное естественное преобразование , которое вписывается в коммутативную диаграмму:${\displaystyle L:\mathbf {B} \to \mathbf {C} }$${\displaystyle \eta :X\to LF}$${\displaystyle M:\mathbf {B} \to \mathbf {C} }$${\displaystyle \alpha :X\to MF}$${\displaystyle \sigma :L\to M}$

где — естественное преобразование с для любого объекта .${\displaystyle \сигма _{F}}$${\displaystyle \sigma _{F}(a)=\sigma (Fa):LF(a)\to MF(a)}$${\displaystyle а}$${\displaystyle \mathbf {A} }$

Функтор L часто записывается как .${\displaystyle \operatorname {Lan} _{F}X}$

Использование слова "the" (как в "the left Kan extension") оправдано тем фактом, что, как и во всех универсальных конструкциях, если определяемый объект существует, то он единственен с точностью до единственного изоморфизма . В этом случае это означает, что (для левых расширений Кана) если есть два левых расширения Кана вдоль , а есть соответствующие преобразования, то существует единственный изоморфизм функторов, такой что вторая диаграмма выше коммутирует. Аналогично для правых расширений Кана.${\displaystyle Л,М}$${\displaystyle X}$${\displaystyle F}$${\displaystyle \эта ,\альфа }$${\displaystyle \sigma :L\to M}$

Предположим, что и — два функтора. Если A — малый , а C — кополный, то существует левое расширение Кана вдоль , определенное на каждом объекте b из B как${\displaystyle X:\mathbf {A} \to \mathbf {C} }$${\displaystyle F:\mathbf {A} \to \mathbf {B} }$${\displaystyle \operatorname {Lan} _{F}X}$${\displaystyle X}$${\displaystyle F}$

${\displaystyle (\operatorname {Lan} _{F}X)(b)=\varinjlim _{f:Fa\to b}X(a)}$

где копредел берется по категории запятой , где — постоянный функтор. Двойственно, если A мало, а C полно, то существуют правые расширения Кана вдоль и могут быть вычислены как предел ${\displaystyle (F\downarrow \operatorname {const} _{b})}$${\displaystyle \operatorname {const} _{b}\colon \ast \to \mathbf {B} ,\ast \mapsto b}$${\displaystyle F}$

${\displaystyle (\operatorname {Ran} _{F}X)(b)=\varprojlim _{Fa\leftarrow b}X(a)}$

над категорией запятой .${\displaystyle (\operatorname {const} _{b}\downarrow F)}$

Предположим, что и являются двумя функторами, такими, что для всех объектов a и a ′ из A и всех объектов b из B существуют костепени в C. Тогда функтор X имеет левое расширение Кана вдоль F , которое таково, что для каждого объекта b из B${\displaystyle X:\mathbf {A} \to \mathbf {C} }$${\displaystyle F:\mathbf {A} \to \mathbf {B} }$${\displaystyle \mathbf {B} (Fa',b)\cdot Xa}$${\displaystyle \operatorname {Lan} _{F}X}$

${\displaystyle (\operatorname {Lan} _{F}X)b =\int ^{a}\mathbf {B} (Fa,b)\cdot Xa}$

когда указанный выше коденд существует для каждого объекта b из B.

Двойственно, правые расширения Кана могут быть вычислены по конечной формуле

${\displaystyle (\operatorname {Ran} _{F}X)b=\int _{a}Xa^{\mathbf {B} (b,Fa)}.}$

Предел функтора может быть выражен как расширение Кана следующим образом :${\displaystyle F:\mathbf {C} \to \mathbf {D} }$

${\displaystyle \lim F=\operatorname {Ran} _{E}F}$

где — уникальный функтор из в ( категория с одним объектом и одной стрелкой, конечный объект в ). Копредел может быть выражен аналогично с помощью${\displaystyle E}$${\displaystyle \mathbf {C} }$${\displaystyle \mathbf {1} }$${\displaystyle \mathbf {Кот} }$${\displaystyle F}$

${\displaystyle \operatorname {colim} F=\operatorname {Lan} _{E}F.}$

Функтор обладает левым сопряженным тогда и только тогда, когда существует правое расширение Кана вдоль и сохраняется . В этом случае левый сопряженный задается и это расширение Кана сохраняется даже любым функтором , т.е. является абсолютным расширением Кана.${\displaystyle F:\mathbf {C} \to \mathbf {D} }$ ${\displaystyle \operatorname {Id} :\mathbf {C} \to \mathbf {C} }$${\displaystyle F}$${\displaystyle F}$${\displaystyle \operatorname {Ran} _{F}\operatorname {Id} }$${\displaystyle \mathbf {C} \to \mathbf {E}}$

Двойственно, правый сопряженный элемент существует тогда и только тогда, когда левое расширение Кана тождества вдоль существует и сохраняется при .${\displaystyle F}$${\displaystyle F}$

Монада коденситности функтора является правым расширением Кана группы G вдоль себя.${\displaystyle G:\mathbf {D} \to \mathbf {C} }$

• Картан, Анри ; Эйленберг, Сэмюэл (1956). Гомологическая алгебра . Princeton Mathematical Series. Том 19. Принстон, Нью-Джерси: Princeton University Press . Zbl  0075.24305.
• Mac Lane, Saunders (1998). Категории для работающих математиков . Graduate Texts in Mathematics . Vol. 5 (2nd ed.). New York, NY: Springer-Verlag . ISBN 0-387-98403-8. Збл  0906.18001.

• Модельно-независимое доказательство формулы копредела для левых расширений Кана
• Расширение Kan в n Lab
• Расширение Кана как предел: пример