Четырехвекторный

Часть серии статей о
Пространство-время
Специальная теория относительности Общая теория относительности
Концепции пространства-времени Пространственно-временное многообразие Принцип эквивалентности Преобразования Лоренца пространство Минковского
Общая теория относительности Введение в общую теорию относительности Математика общей теории относительности Уравнения поля Эйнштейна
Классическая гравитация Введение в гравитацию Закон всемирного тяготения Ньютона
Соответствующая математика Четырехвекторный Выводы теории относительности Диаграммы пространства-времени Дифференциальная геометрия Изогнутое пространство Искривленное пространство-время Математика общей теории относительности Топология пространства-времени
Физический портал  Категория
в т е

В специальной теории относительности 4-вектор ( или 4-вектор , иногда вектор Лоренца ) ^[1] — это объект с четырьмя компонентами, которые преобразуются определенным образом при преобразованиях Лоренца . В частности, 4-вектор — это элемент четырехмерного векторного пространства, рассматриваемого как пространство представления стандартного представления группы Лоренца , ( ⁠1/2⁠ , ⁠1/2⁠ ) ​​представление. Он отличается от евклидова вектора тем, как определяется его величина. Преобразования, которые сохраняют эту величину, — это преобразования Лоренца, которые включают пространственные вращения и ускорения (изменение на постоянную скорость в другую инерциальную систему отсчета ). ^{[2] : ch1}

Четырехвекторы описывают, например, положение x ^μ в пространстве-времени, моделируемом как пространство Минковского , четырехимпульс частицы p ^μ , амплитуду электромагнитного четырехпотенциала A ^μ ( x ) в точке x в пространстве-времени и элементы подпространства, охватываемого гамма-матрицами внутри алгебры Дирака .

Группа Лоренца может быть представлена ​​матрицами 4×4 Λ . Действие преобразования Лоренца на общий контравариантный четырехвектор X (подобно примерам выше), рассматриваемый как вектор-столбец с декартовыми координатами относительно инерциальной системы отсчета в записях, задается выражением

$${\displaystyle X'=\Лямбда X,}$$

(умножение матриц), где компоненты штрихованного объекта относятся к новому кадру. Связанные с примерами выше, которые даны как контравариантные векторы, существуют также соответствующие ковариантные векторы x _μ , p _μ и A _μ ( x ) . Они преобразуются согласно правилу

$${\displaystyle X'=\left(\Lambda ^{-1}\right)^{\textrm {T}}X,}$$

где ^T обозначает транспонированную матрицу . Это правило отличается от правила выше. Оно соответствует дуальному представлению стандартного представления. Однако для группы Лоренца дуальное представление любого представления эквивалентно исходному представлению. Таким образом, объекты с ковариантными индексами также являются 4-векторами.

Пример хорошо ведущего себя четырехкомпонентного объекта в специальной теории относительности, который не является четырехвектором, см. биспинор . Он определяется аналогичным образом, разница в том, что правило преобразования при преобразованиях Лоренца задается представлением, отличным от стандартного представления. В этом случае правило имеет вид X ′ = Π(Λ) X , где Π(Λ) — матрица 4×4, отличная от Λ . Аналогичные замечания применимы к объектам с меньшим или большим количеством компонентов, которые хорошо ведут себя при преобразованиях Лоренца. К ним относятся скаляры , спиноры , тензоры и спинор-тензоры.

В статье рассматриваются четырехвекторы в контексте специальной теории относительности. Хотя концепция четырехвекторов распространяется и на общую теорию относительности , некоторые из результатов, изложенных в этой статье, требуют модификации в общей теории относительности.

В данной статье используются следующие обозначения: строчные полужирные для трехмерных векторов, шляпки для трехмерных единичных векторов , заглавные полужирные для четырехмерных векторов (за исключением четырехградиента) и обозначение индекса тензора .

Четырехмерный вектор A — это вектор с «временным» компонентом и тремя «пространственными» компонентами, который может быть записан в различных эквивалентных обозначениях: ^[3]

$${\displaystyle {\begin{aligned}\mathbf {A} &=\left(A^{0},\,A^{1},\,A^{2},\,A^{3}\right)\\&=A^{0}\mathbf {E} _{0}+A^{1}\mathbf {E} _{1}+A^{2}\mathbf {E} _{2}+A^{3}\mathbf {E} _{3}\\&=A^{0}\mathbf {E} _{0}+A^{i}\mathbf {E} _{i}\\&=A^{\alpha }\mathbf {E} _{\alpha }\end{aligned}}}$$

где A ^α — компонент величины, а E _α — компонент базисного вектора ; следует отметить, что оба компонента необходимы для создания вектора, и что когда A ^α рассматривается отдельно, он относится строго к компонентам вектора.

Верхние индексы указывают на контравариантные компоненты. Здесь стандартное соглашение заключается в том, что латинские индексы принимают значения для пространственных компонентов, так что i = 1, 2, 3, а греческие индексы принимают значения для пространственных и временных компонентов, так что α = 0, 1, 2, 3, используемых с соглашением о суммировании . Разделение между временным компонентом и пространственными компонентами полезно при определении сокращений одного четырехвектора с другими тензорными величинами, например, для вычисления инвариантов Лоренца во внутренних произведениях (примеры приведены ниже) или повышения и понижения индексов .

В специальной теории относительности пространственноподобный базис E ₁ , E ₂ , E ₃ и компоненты A ¹ , A ² , A ³ часто являются декартовыми базисом и компонентами:

$${\displaystyle {\begin{align}\mathbf {A} &=\left(A_{t},\,A_{x},\,A_{y},\,A_{z}\right)\\&=A_{t}\mathbf {E} _{t}+A_{x}\mathbf {E} _{x}+A_{y}\mathbf {E} _{y}+A_{z}\mathbf {E} _{z}\\\end{align}}}$$

хотя, конечно, могут быть использованы любые другие базисы и компоненты, например, сферические полярные координаты

$${\displaystyle {\begin{aligned}\mathbf {A} &=\left(A_{t},\,A_{r},\,A_{\theta },\,A_{\phi }\right)\\&=A_{t}\mathbf {E} _{t}+A_{r}\mathbf {E} _{r}+A_{\theta }\mathbf {E} _{\theta }+A_{\phi }\mathbf {E} _{\phi }\\\end{aligned}}}$$

или цилиндрические полярные координаты ,

$${\displaystyle {\begin{aligned}\mathbf {A} &=(A_{t},\,A_{r},\,A_{\theta },\,A_{z})\\&=A_{t}\mathbf {E} _{t}+A_{r}\mathbf {E} _{r}+A_{\theta }\mathbf {E} _{\theta }+A_{z}\mathbf {E} _{z}\\\end{aligned}}}$$

или любые другие ортогональные координаты , или даже общие криволинейные координаты . Обратите внимание, что метки координат всегда индексируются как метки и не являются индексами, принимающими числовые значения. В общей теории относительности должны использоваться локальные криволинейные координаты в локальном базисе. Геометрически четырехвектор все еще может интерпретироваться как стрелка, но в пространстве-времени — не только в пространстве. В теории относительности стрелки рисуются как часть диаграммы Минковского (также называемой диаграммой пространства-времени ). В этой статье четырехвекторы будут называться просто векторами.

Также принято представлять основания векторами-столбцами :

$${\displaystyle \mathbf {E} _{0}={\begin{pmatrix}1\\0\\0\\0\end{pmatrix}}\,,\quad \mathbf {E} _{1}={\begin{pmatrix}0\\1\\0\\0\end{pmatrix}}\,,\quad \mathbf {E} _{2}={\begin{pmatrix}0\\0\\1\\0\end{pmatrix}}\,,\quad \mathbf {E} _{3}={\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}}$$

так что:

$${\displaystyle \mathbf {A} ={\begin{pmatrix}A^{0}\\A^{1}\\A^{2}\\A^{3}\end{pmatrix}}}$$

Связь между ковариантными и контравариантными координатами осуществляется через метрический тензор Минковского (называемый метрикой), η , который повышает и понижает индексы следующим образом:

$${\displaystyle A_{\mu }=\eta _{\mu \nu }A^{\nu }\,,}$$

и в различных эквивалентных обозначениях ковариантные компоненты имеют вид:

$${\displaystyle {\begin{aligned}\mathbf {A} &=(A_{0},\,A_{1},\,A_{2},\,A_{3})\\&=A_{0}\mathbf {E} ^{0}+A_{1}\mathbf {E} ^{1}+A_{2}\mathbf {E} ^{2}+A_{3}\mathbf {E} ^{3}\\&=A_{0}\mathbf {E} ^{0}+A_{i}\mathbf {E} ^{i}\\&=A_{\alpha }\mathbf {E} ^{\alpha }\\\end{aligned}}}$$

где пониженный индекс указывает на то, что он ковариантный . Часто метрика является диагональной, как в случае ортогональных координат (см. элемент линии ), но не в общих криволинейных координатах .

Базы могут быть представлены векторами-строками :

$${\displaystyle \mathbf {E} ^{0}={\begin{pmatrix}1&0&0&0\end{pmatrix}}\,,\quad \mathbf {E} ^{1}={\begin{pmatrix}0&1&0&0\end{pmatrix}}\,,\quad \mathbf {E} ^{2}={\begin{pmatrix}0&0&1&0\end{pmatrix}}\,,\quad \mathbf {E} ^{3}={\begin{pmatrix}0&0&0&1\end{pmatrix}}}$$так что:$${\displaystyle \mathbf {A} ={\begin{pmatrix}A_{0}&A_{1}&A_{2}&A_{3}\end{pmatrix}}}$$

Мотивация вышеуказанных соглашений заключается в том, что внутренний продукт является скаляром, подробности см. ниже.

При наличии двух инерциальных или повернутых систем отсчета четырехвектор определяется как величина, которая преобразуется в соответствии с матрицей  преобразования Лоренца Λ :$${\displaystyle \mathbf {A} '={\boldsymbol {\Lambda }}\mathbf {A} }$$

В индексной записи контравариантные и ковариантные компоненты преобразуются согласно, соответственно: где матрица Λ имеет компоненты Λ ^μ _ν в строке  μ и столбце  ν , а матрица ( Λ ⁻¹ ) ^T имеет компоненты Λ _μ ^ν в строке  μ и столбце  ν .$${\displaystyle {A'}^{\mu }=\Lambda ^{\mu }{}_{\nu }A^{\nu }\,,\quad {A'}_{\mu }=\Lambda _{\mu }{}^{\nu }A_{\nu }}$$

Для получения справочной информации о природе этого определения преобразования см. тензор . Все четырехвекторы преобразуются одинаково, и это можно обобщить на четырехмерные релятивистские тензоры; см. специальную теорию относительности .

Для двух систем, повернутых на фиксированный угол θ вокруг оси, определяемой единичным вектором :

$${\displaystyle {\hat {\mathbf {n} }}=\left({\hat {n}}_{1},{\hat {n}}_{2},{\hat {n}}_{3}\right)\,,}$$

Без каких-либо улучшений матрица Λ имеет компоненты, заданные следующим образом: ^[4]

$${\displaystyle {\begin{aligned}\Lambda _{00}&=1\\\Lambda _{0i}=\Lambda _{i0}&=0\\\Lambda _{ij}&=\left(\delta _{ij}-{\hat {n}}_{i}{\hat {n}}_{j}\right)\cos \theta -\varepsilon _{ijk}{\hat {n}}_{k}\sin \theta +{\hat {n}}_{i}{\hat {n}}_{j}\end{aligned}}}$$

где δ _ij — символ Кронекера , а ε _ijk — трехмерный символ Леви-Чивиты . Пространственноподобные компоненты четырехвекторов поворачиваются, тогда как времениподобные компоненты остаются неизменными.

Для случая вращения только вокруг оси z пространственноподобная часть матрицы Лоренца сводится к матрице вращения вокруг оси z :

$${\displaystyle {\begin{pmatrix}{A'}^{0}\\{A'}^{1}\\{A'}^{2}\\{A'}^{3}\end{pmatrix}}={\begin{pmatrix}1&0&0&0\\0&\cos \theta &-\sin \theta &0\\0&\sin \theta &\cos \theta &0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}A^{0}\\A^{1}\\A^{2}\\A^{3}\end{pmatrix}}\ .}$$

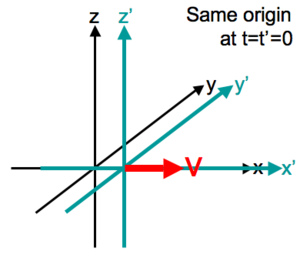
Для двух систем отсчета, движущихся с постоянной относительной трехскоростью v (не четырехскоростью, см. ниже), удобно обозначить и определить относительную скорость в единицах c следующим образом:

$${\displaystyle {\boldsymbol {\beta }}=(\beta _{1},\,\beta _{2},\,\beta _{3})={\frac {1}{c}}(v_{1},\,v_{2},\,v_{3})={\frac {1}{c}}\mathbf {v} \,.}$$

Тогда без вращений матрица Λ имеет компоненты, заданные как: ^[5] где фактор Лоренца определяется как: и δ _ij — дельта Кронекера . В отличие от случая чистых вращений, пространственноподобные и времениподобные компоненты смешиваются при усилениях.$${\displaystyle {\begin{aligned}\Lambda _{00}&=\gamma ,\\\Lambda _{0i}=\Lambda _{i0}&=-\gamma \beta _{i},\\\Lambda _{ij}=\Lambda _{ji}&=(\gamma -1){\frac {\beta _{i}\beta _{j}}{\beta ^{2}}}+\delta _{ij}=(\gamma -1){\frac {v_{i}v_{j}}{v^{2}}}+\delta _{ij},\\\end{aligned}}}$$$${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\boldsymbol {\beta }}\cdot {\boldsymbol {\beta }}}}}\,,}$$

Для случая усиления только в направлении x матрица уменьшается до: ^{[6] [7]}

$${\displaystyle {\begin{pmatrix}A'^{0}\\A'^{1}\\A'^{2}\\A'^{3}\end{pmatrix}}={\begin{pmatrix}\cosh \phi &-\sinh \phi &0&0\\-\sinh \phi &\cosh \phi &0&0\\0&0&1&0\\0&0&0&1\\\end{pmatrix}}{\begin{pmatrix}A^{0}\\A^{1}\\A^{2}\\A^{3}\end{pmatrix}}}$$

Где было использовано выражение быстроты ϕ , записанное через гиперболические функции :$${\displaystyle \gamma =\cosh \phi }$$

Эта матрица Лоренца иллюстрирует усиление как гиперболическое вращение в четырехмерном пространстве-времени, аналогичное круговому вращению, описанному выше в трехмерном пространстве.

Четырехмерные векторы имеют те же линейные свойства, что и евклидовы векторы в трех измерениях . Их можно складывать обычным поэлементным способом: и аналогично скалярное умножение на скаляр λ определяется поэлементным способом:$${\displaystyle \mathbf {A} +\mathbf {B} =\left(A^{0},A^{1},A^{2},A^{3}\right)+\left(B^{0},B^{1},B^{2},B^{3}\right)=\left(A^{0}+B^{0},A^{1}+B^{1},A^{2}+B^{2},A^{3}+B^{3}\right)}$$ $${\displaystyle \lambda \mathbf {A} =\lambda \left(A^{0},A^{1},A^{2},A^{3}\right)=\left(\lambda A^{0},\lambda A^{1},\lambda A^{2},\lambda A^{3}\right)}$$

Тогда вычитание является обратной операцией сложения, определяемой поэлементно следующим образом:$${\displaystyle \mathbf {A} +(-1)\mathbf {B} =\left(A^{0},A^{1},A^{2},A^{3}\right)+(-1)\left(B^{0},B^{1},B^{2},B^{3}\right)=\left(A^{0}-B^{0},A^{1}-B^{1},A^{2}-B^{2},A^{3}-B^{3}\right)}$$

Применяя тензор Минковского η _μν к двум 4-векторам A и B , записывая результат в виде скалярного произведения , имеем, используя обозначения Эйнштейна :$${\displaystyle \mathbf {A} \cdot \mathbf {B} =A^{\mu }B^{\nu }\mathbf {E} _{\mu }\cdot \mathbf {E} _{\nu }=A^{\mu }\eta _{\mu \nu }B^{\nu }}$$

в специальной теории относительности. Скалярное произведение базисных векторов является метрикой Минковского, в отличие от дельты Кронекера, как в евклидовом пространстве. Удобно переписать определение в матричной форме: в этом случае η _μν выше является записью в строке μ и столбце ν метрики Минковского как квадратной матрицы. Метрика Минковского не является евклидовой метрикой , поскольку она неопределенна (см. сигнатуру метрики ). Можно использовать ряд других выражений, поскольку метрический тензор может повышать и понижать компоненты A или B. Для контра/ковариантных компонентов A и ко/контравариантных компонентов B мы имеем: так что в матричной записи: в то время как для A и B каждый в ковариантных компонентах: с матричным выражением, аналогичным приведенному выше.$${\displaystyle \mathbf {A\cdot B} ={\begin{pmatrix}A^{0}&A^{1}&A^{2}&A^{3}\end{pmatrix}}{\begin{pmatrix}\eta _{00}&\eta _{01}&\eta _{02}&\eta _{03}\\\eta _{10}&\eta _{11}&\eta _{12}&\eta _{13}\\\eta _{20}&\eta _{21}&\eta _{22}&\eta _{23}\\\eta _{30}&\eta _{31}&\eta _{32}&\eta _{33}\end{pmatrix}}{\begin{pmatrix}B^{0}\\B^{1}\\B^{2}\\B^{3}\end{pmatrix}}}$$$${\displaystyle \mathbf {A} \cdot \mathbf {B} =A^{\mu }\eta _{\mu \nu }B^{\nu }=A_{\nu }B^{\nu }=A^{\mu }B_{\mu }}$$$${\displaystyle \mathbf {A} \cdot \mathbf {B} ={\begin{pmatrix}A_{0}&A_{1}&A_{2}&A_{3}\end{pmatrix}}{\begin{pmatrix}B^{0}\\B^{1}\\B^{2}\\B^{3}\end{pmatrix}}={\begin{pmatrix}B_{0}&B_{1}&B_{2}&B_{3}\end{pmatrix}}{\begin{pmatrix}A^{0}\\A^{1}\\A^{2}\\A^{3}\end{pmatrix}}}$$$${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{\mu }\eta ^{\mu \nu }B_{\nu }}$$

Применяя тензор Минковского к четырехмерному вектору A с самим собой, получаем: что, в зависимости от случая, можно считать квадратом или его отрицательным значением длины вектора.$${\displaystyle \mathbf {A\cdot A} =A^{\mu }\eta _{\mu \nu }A^{\nu }}$$

Ниже приведены два распространенных выбора для метрического тензора в стандартном базисе (по сути, декартовы координаты). Если используются ортогональные координаты, то будут масштабные коэффициенты вдоль диагональной части пространственноподобной части метрики, в то время как для общих криволинейных координат вся пространственноподобная часть метрики будет иметь компоненты, зависящие от используемого криволинейного базиса.

Метрическую сигнатуру (+−−−) иногда называют «в основном минусовой» конвенцией или конвенцией «западного побережья».

В метрической сигнатуре (+−−−) оценка суммирования по индексам дает: тогда как в матричной форме:$${\displaystyle \mathbf {A} \cdot \mathbf {B} =A^{0}B^{0}-A^{1}B^{1}-A^{2}B^{2}-A^{3}B^{3}}$$$${\displaystyle \mathbf {A\cdot B} ={\begin{pmatrix}A^{0}&A^{1}&A^{2}&A^{3}\end{pmatrix}}{\begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}}{\begin{pmatrix}B^{0}\\B^{1}\\B^{2}\\B^{3}\end{pmatrix}}}$$

Это повторяющаяся тема в специальной теории относительности: взять выражение в одной системе отсчета , где C — значение внутреннего произведения в этой системе, и: в другой системе отсчета, в которой C ′ — значение внутреннего произведения в этой системе. Тогда, поскольку внутреннее произведение является инвариантом, они должны быть равны: то есть:$${\displaystyle \mathbf {A} \cdot \mathbf {B} =A^{0}B^{0}-A^{1}B^{1}-A^{2}B^{2}-A^{3}B^{3}=C}$$$${\displaystyle \mathbf {A} '\cdot \mathbf {B} '={A'}^{0}{B'}^{0}-{A'}^{1}{B'}^{1}-{A'}^{2}{B'}^{2}-{A'}^{3}{B'}^{3}=C'}$$$${\displaystyle \mathbf {A} \cdot \mathbf {B} =\mathbf {A} '\cdot \mathbf {B} '}$$$${\displaystyle C=A^{0}B^{0}-A^{1}B^{1}-A^{2}B^{2}-A^{3}B^{3}={A'}^{0}{B'}^{0}-{A'}^{1}{B'}^{1}-{A'}^{2}{B'}^{2}-{A'}^{3}{B'}^{3}}$$

Учитывая, что физические величины в теории относительности являются четырехвекторами, это уравнение имеет вид « закона сохранения », но никакого «сохранения» не задействовано. Основное значение скалярного произведения Минковского состоит в том, что для любых двух четырехвекторов его значение инвариантно для всех наблюдателей; изменение координат не приводит к изменению значения скалярного произведения. Компоненты четырехвекторов изменяются от одной системы к другой; A и A ′ связаны преобразованием Лоренца , и аналогично для B и B ′, хотя скалярные произведения одинаковы во всех системах. Тем не менее, этот тип выражения используется в релятивистских вычислениях наравне с законами сохранения, поскольку величины компонентов могут быть определены без явного выполнения каких-либо преобразований Лоренца. Конкретный пример — энергия и импульс в соотношении энергия-импульс, полученном из вектора четырехимпульса (см. также ниже).

В этой подписи мы имеем:$${\displaystyle \mathbf {A\cdot A} =\left(A^{0}\right)^{2}-\left(A^{1}\right)^{2}-\left(A^{2}\right)^{2}-\left(A^{3}\right)^{2}}$$

С сигнатурой (+−−−) 4-векторы можно классифицировать как пространственноподобные , если , времениподобные , если , и нулевые векторы , если .${\displaystyle \mathbf {A\cdot A} <0}$${\displaystyle \mathbf {A\cdot A} >0}$${\displaystyle \mathbf {A\cdot A} =0}$

Метрическую сигнатуру (-+++) иногда называют конвенцией «восточного побережья».

Некоторые авторы определяют η с обратным знаком, в этом случае мы имеем метрическую сигнатуру (−+++). Оценка суммирования с этой сигнатурой:

$${\displaystyle \mathbf {A\cdot B} =-A^{0}B^{0}+A^{1}B^{1}+A^{2}B^{2}+A^{3}B^{3}}$$

в то время как матричная форма имеет вид:

$${\displaystyle \mathbf {A\cdot B} =\left({\begin{matrix}A^{0}&A^{1}&A^{2}&A^{3}\end{matrix}}\right)\left({\begin{matrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{matrix}}\right)\left({\begin{matrix}B^{0}\\B^{1}\\B^{2}\\B^{3}\end{matrix}}\right)}$$

Обратите внимание, что в этом случае в одном кадре:

$${\displaystyle \mathbf {A} \cdot \mathbf {B} =-A^{0}B^{0}+A^{1}B^{1}+A^{2}B^{2}+A^{3}B^{3}=-C}$$

а в другом:

$${\displaystyle \mathbf {A} '\cdot \mathbf {B} '=-{A'}^{0}{B'}^{0}+{A'}^{1}{B'}^{1}+{A'}^{2}{B'}^{2}+{A'}^{3}{B'}^{3}=-C'}$$

так что:

$${\displaystyle -C=-A^{0}B^{0}+A^{1}B^{1}+A^{2}B^{2}+A^{3}B^{3}=-{A'}^{0}{B'}^{0}+{A'}^{1}{B'}^{1}+{A'}^{2}{B'}^{2}+{A'}^{3}{B'}^{3}}$$

что эквивалентно приведенному выше выражению для C в терминах A и B. Любое соглашение будет работать. При метрике Минковского, определенной двумя способами выше, единственное различие между ковариантными и контравариантными четырехвекторными компонентами — это знаки, поэтому знаки зависят от того, какое соглашение о знаках используется.

У нас есть:

$${\displaystyle \mathbf {A\cdot A} =-\left(A^{0}\right)^{2}+\left(A^{1}\right)^{2}+\left(A^{2}\right)^{2}+\left(A^{3}\right)^{2}}$$

С сигнатурой (−+++) 4-векторы можно классифицировать как пространственноподобные , если , времениподобные , если , и нулевые , если .${\displaystyle \mathbf {A\cdot A} >0}$${\displaystyle \mathbf {A\cdot A} <0}$${\displaystyle \mathbf {A\cdot A} =0}$

Применение тензора Минковского часто выражается как влияние дуального вектора одного вектора на другой:

$${\displaystyle \mathbf {A\cdot B} =A^{*}(\mathbf {B} )=A{_{\nu }}B^{\nu }.}$$

Здесь A _ν s являются компонентами дуального вектора A * вектора A в дуальном базисе и называются ковариантными координатами A , тогда как исходные компоненты A ^ν называются контравариантными координатами.

В специальной теории относительности (но не в общей теории относительности) производная 4-вектора по скаляру λ (инварианту) сама является 4-вектором. Также полезно взять дифференциал 4 -вектора, d A , и разделить его на дифференциал скаляра, dλ :

$${\displaystyle {\underset {\text{differential}}{d\mathbf {A} }}={\underset {\text{derivative}}{\frac {d\mathbf {A} }{d\lambda }}}{\underset {\text{differential}}{d\lambda }}}$$

где контравариантные компоненты:

$${\displaystyle d\mathbf {A} =\left(dA^{0},dA^{1},dA^{2},dA^{3}\right)}$$

в то время как ковариантные компоненты:

$${\displaystyle d\mathbf {A} =\left(dA_{0},dA_{1},dA_{2},dA_{3}\right)}$$

В релятивистской механике часто берут дифференциал четырехвектора и делят на дифференциал в собственном времени (см. ниже).

Точка в пространстве Минковского — это временное и пространственное положение, называемое «событием», или иногда положением четырехвектора или четырехпозиционным или 4-позиционным , описываемым в некоторой системе отсчета набором из четырех координат:

$${\displaystyle \mathbf {R} =\left(ct,\mathbf {r} \right)}$$

где r — вектор положения в трехмерном пространстве . Если r — функция координатного времени t в той же системе отсчета, т. е. r = r ( t ), это соответствует последовательности событий при изменении t . Определение R ⁰ = ct гарантирует, что все координаты имеют одинаковую размерность ( длину ) и единицы (в СИ — метры). ^{[8] [9] [10] [11]} Эти координаты являются компонентами четырехвектора положения для события.

Четырехвектор смещения определяется как «стрелка», связывающая два события:

$${\displaystyle \Delta \mathbf {R} =\left(c\Delta t,\Delta \mathbf {r} \right)}$$

Для дифференциальной четырехпозиционности на мировой линии имеем, используя норменную нотацию :

$${\displaystyle \|d\mathbf {R} \|^{2}=\mathbf {dR\cdot dR} =dR^{\mu }dR_{\mu }=c^{2}d\tau ^{2}=ds^{2}\,,}$$

определяя элемент дифференциальной линии d s и приращение собственного дифференциального времени d τ , но эта «норма» также:

$${\displaystyle \|d\mathbf {R} \|^{2}=(cdt)^{2}-d\mathbf {r} \cdot d\mathbf {r} \,,}$$

так что:

$${\displaystyle (cd\tau )^{2}=(cdt)^{2}-d\mathbf {r} \cdot d\mathbf {r} \,.}$$

При рассмотрении физических явлений дифференциальные уравнения возникают естественным образом; однако при рассмотрении производных функций по пространству и времени неясно, относительно какой системы отсчета берутся эти производные. Принято считать, что производные по времени берутся относительно собственного времени . Поскольку собственное время является инвариантом, это гарантирует, что производная по собственному времени любого четырехвектора сама является четырехвектором. Затем важно найти связь между этой производной по собственному времени и другой производной по времени (используя координатное время t инерциальной системы отсчета). Эта связь обеспечивается путем взятия вышеуказанного дифференциального инвариантного интервала пространства-времени, а затем деления его на ( cdt ) ² для получения:${\displaystyle \tau }$

$${\displaystyle \left({\frac {cd\tau }{cdt}}\right)^{2}=1-\left({\frac {d\mathbf {r} }{cdt}}\cdot {\frac {d\mathbf {r} }{cdt}}\right)=1-{\frac {\mathbf {u} \cdot \mathbf {u} }{c^{2}}}={\frac {1}{\gamma (\mathbf {u} )^{2}}}\,,}$$

где u = dr / dt - координатная 3- скорость объекта, измеренная в той же системе отсчета, что и координаты x , y , z и координатное время t , и

$${\displaystyle \gamma (\mathbf {u} )={\frac {1}{\sqrt {1-{\frac {\mathbf {u} \cdot \mathbf {u} }{c^{2}}}}}}}$$

является фактором Лоренца . Это обеспечивает полезное соотношение между дифференциалами в координатном времени и собственном времени:

$${\displaystyle dt=\gamma (\mathbf {u} )d\tau \,.}$$

Это соотношение можно также найти из преобразования времени в преобразованиях Лоренца .

Важные четырехвекторы в теории относительности можно определить, применяя этот дифференциал .${\displaystyle {\frac {d}{d\tau }}}$

Учитывая, что частные производные являются линейными операторами , можно образовать четырехградиент из частной производной по времени ∂ / ∂ t и пространственного градиента ∇. Используя стандартный базис, в индексных и сокращенных обозначениях контравариантные компоненты имеют вид:

$${\displaystyle {\begin{aligned}{\boldsymbol {\partial }}&=\left({\frac {\partial }{\partial x_{0}}},\,-{\frac {\partial }{\partial x_{1}}},\,-{\frac {\partial }{\partial x_{2}}},\,-{\frac {\partial }{\partial x_{3}}}\right)\\&=(\partial ^{0},\,-\partial ^{1},\,-\partial ^{2},\,-\partial ^{3})\\&=\mathbf {E} _{0}\partial ^{0}-\mathbf {E} _{1}\partial ^{1}-\mathbf {E} _{2}\partial ^{2}-\mathbf {E} _{3}\partial ^{3}\\&=\mathbf {E} _{0}\partial ^{0}-\mathbf {E} _{i}\partial ^{i}\\&=\mathbf {E} _{\alpha }\partial ^{\alpha }\\&=\left({\frac {1}{c}}{\frac {\partial }{\partial t}},\,-\nabla \right)\\&=\left({\frac {\partial _{t}}{c}},-\nabla \right)\\&=\mathbf {E} _{0}{\frac {1}{c}}{\frac {\partial }{\partial t}}-\nabla \\\end{aligned}}}$$

Обратите внимание, что базисные векторы помещены перед компонентами, чтобы избежать путаницы между взятием производной базисного вектора или простым указанием частной производной как компонента этого четырехвектора. Ковариантные компоненты:

$${\displaystyle {\begin{aligned}{\boldsymbol {\partial }}&=\left({\frac {\partial }{\partial x^{0}}},\,{\frac {\partial }{\partial x^{1}}},\,{\frac {\partial }{\partial x^{2}}},\,{\frac {\partial }{\partial x^{3}}}\right)\\&=(\partial _{0},\,\partial _{1},\,\partial _{2},\,\partial _{3})\\&=\mathbf {E} ^{0}\partial _{0}+\mathbf {E} ^{1}\partial _{1}+\mathbf {E} ^{2}\partial _{2}+\mathbf {E} ^{3}\partial _{3}\\&=\mathbf {E} ^{0}\partial _{0}+\mathbf {E} ^{i}\partial _{i}\\&=\mathbf {E} ^{\alpha }\partial _{\alpha }\\&=\left({\frac {1}{c}}{\frac {\partial }{\partial t}},\,\nabla \right)\\&=\left({\frac {\partial _{t}}{c}},\nabla \right)\\&=\mathbf {E} ^{0}{\frac {1}{c}}{\frac {\partial }{\partial t}}+\nabla \\\end{aligned}}}$$

Поскольку это оператор, у него нет «длины», но вычисление внутреннего произведения оператора с самим собой дает другой оператор:

$${\displaystyle \partial ^{\mu }\partial _{\mu }={\frac {1}{c^{2}}}{\frac {\partial ^{2}}{\partial t^{2}}}-\nabla ^{2}={\frac {{\partial _{t}}^{2}}{c^{2}}}-\nabla ^{2}}$$

называемый оператором Даламбера .

Четырехскорость частицы определяется как :

$${\displaystyle \mathbf {U} ={\frac {d\mathbf {X} }{d\tau }}={\frac {d\mathbf {X} }{dt}}{\frac {dt}{d\tau }}=\gamma (\mathbf {u} )\left(c,\mathbf {u} \right),}$$

Геометрически U — нормированный вектор, касательный к мировой линии частицы. Используя дифференциал четырехпозиционности, можно получить величину четырехскорости:

$${\displaystyle \|\mathbf {U} \|^{2}=U^{\mu }U_{\mu }={\frac {dX^{\mu }}{d\tau }}{\frac {dX_{\mu }}{d\tau }}={\frac {dX^{\mu }dX_{\mu }}{d\tau ^{2}}}=c^{2}\,,}$$

Короче говоря, величина 4-скорости для любого объекта всегда является фиксированной константой:

$${\displaystyle \|\mathbf {U} \|^{2}=c^{2}}$$

Норма также:

$${\displaystyle \|\mathbf {U} \|^{2}={\gamma (\mathbf {u} )}^{2}\left(c^{2}-\mathbf {u} \cdot \mathbf {u} \right)\,,}$$

так что:

$${\displaystyle c^{2}={\gamma (\mathbf {u} )}^{2}\left(c^{2}-\mathbf {u} \cdot \mathbf {u} \right)\,,}$$

что сводится к определению фактора Лоренца .

Единицами четырехскорости являются м/с в СИ и 1 в геометрической системе единиц . Четырехскорость является контравариантным вектором.

Четырехкратное ускорение определяется по формуле:

$${\displaystyle \mathbf {A} ={\frac {d\mathbf {U} }{d\tau }}=\gamma (\mathbf {u} )\left({\frac {d{\gamma }(\mathbf {u} )}{dt}}c,{\frac {d{\gamma }(\mathbf {u} )}{dt}}\mathbf {u} +\gamma (\mathbf {u} )\mathbf {a} \right).}$$

где a = d u / dt - координата 3-ускорения. Поскольку величина U является постоянной, 4-ускорение ортогонально 4-скорости, т.е. внутреннее произведение Минковского 4-ускорения и 4-скорости равно нулю:

$${\displaystyle \mathbf {A} \cdot \mathbf {U} =A^{\mu }U_{\mu }={\frac {dU^{\mu }}{d\tau }}U_{\mu }={\frac {1}{2}}\,{\frac {d}{d\tau }}\left(U^{\mu }U_{\mu }\right)=0\,}$$

что справедливо для всех мировых линий. Геометрический смысл 4-ускорения — это вектор кривизны мировой линии в пространстве Минковского.

Для массивной частицы с массой покоя (или инвариантной массой ) m ₀ 4-импульс определяется выражением:

$${\displaystyle \mathbf {P} =m_{0}\mathbf {U} =m_{0}\gamma (\mathbf {u} )(c,\mathbf {u} )=\left({\frac {E}{c}},\mathbf {p} \right)}$$

где полная энергия движущейся частицы равна:

$${\displaystyle E=\gamma (\mathbf {u} )m_{0}c^{2}}$$

а полный релятивистский импульс равен:

$${\displaystyle \mathbf {p} =\gamma (\mathbf {u} )m_{0}\mathbf {u} }$$

Взяв внутреннее произведение четырехимпульса с самим собой:

$${\displaystyle \|\mathbf {P} \|^{2}=P^{\mu }P_{\mu }=m_{0}^{2}U^{\mu }U_{\mu }=m_{0}^{2}c^{2}}$$

а также:

$${\displaystyle \|\mathbf {P} \|^{2}={\frac {E^{2}}{c^{2}}}-\mathbf {p} \cdot \mathbf {p} }$$

что приводит к соотношению энергии и импульса :

$${\displaystyle E^{2}=c^{2}\mathbf {p} \cdot \mathbf {p} +\left(m_{0}c^{2}\right)^{2}\,.}$$

Последнее соотношение полезно в релятивистской механике , существенно в релятивистской квантовой механике и релятивистской квантовой теории поля , и все они имеют приложения к физике элементарных частиц .

Четырехмерная сила, действующая на частицу, определяется аналогично тройной силе как производная по времени тройного импульса во втором законе Ньютона :

$${\displaystyle \mathbf {F} ={\frac {d\mathbf {P} }{d\tau }}=\gamma (\mathbf {u} )\left({\frac {1}{c}}{\frac {dE}{dt}},{\frac {d\mathbf {p} }{dt}}\right)=\gamma (\mathbf {u} )\left({\frac {P}{c}},\mathbf {f} \right)}$$

где P — мощность, передаваемая для перемещения частицы, а f — 3-сила, действующая на частицу. Для частицы постоянной инвариантной массы m ₀ это эквивалентно

$${\displaystyle \mathbf {F} =m_{0}\mathbf {A} =m_{0}\gamma (\mathbf {u} )\left({\frac {d{\gamma }(\mathbf {u} )}{dt}}c,\left({\frac {d{\gamma }(\mathbf {u} )}{dt}}\mathbf {u} +\gamma (\mathbf {u} )\mathbf {a} \right)\right)}$$

Инвариант, полученный из четырех сил, имеет вид:

$${\displaystyle \mathbf {F} \cdot \mathbf {U} =F^{\mu }U_{\mu }=m_{0}A^{\mu }U_{\mu }=0}$$

из приведенного выше результата.

Поле четырехмерного вектора теплового потока по сути аналогично полю трехмерного вектора теплового потока q в локальной системе координат жидкости: ^[12]

$${\displaystyle \mathbf {Q} =-k{\boldsymbol {\partial }}T=-k\left({\frac {1}{c}}{\frac {\partial T}{\partial t}},\nabla T\right)}$$

где T — абсолютная температура , k — теплопроводность .

Поток барионов равен: [ ^13] где n — плотность числа барионов в локальной системе покоя барионной жидкости (положительные значения для барионов, отрицательные для антибарионов ), а U — четырехскоростное поле (жидкости), как указано выше.$${\displaystyle \mathbf {S} =n\mathbf {U} }$$

Вектор четырехэнтропии определяется как: ^[14] где s — энтропия на барион, а T — абсолютная температура в локальной системе покоя жидкости. ^[15]$${\displaystyle \mathbf {s} =s\mathbf {S} +{\frac {\mathbf {Q} }{T}}}$$

Примерами четырехвекторов в электромагнетизме являются следующие.

Электромагнитный четырехток (или, правильнее сказать, плотность четырехтока) ^[16] определяется как образованный из плотности тока j и плотности заряда ρ .$${\displaystyle \mathbf {J} =\left(\rho c,\mathbf {j} \right)}$$

Электромагнитный четырехпотенциал (или, точнее, четырехэлектродный векторный потенциал), определяемый как образованный из векторного потенциала a и скалярного потенциала ϕ .$${\displaystyle \mathbf {A} =\left({\frac {\phi }{c}},\mathbf {a} \right)}$$

Четырехпотенциал не определяется однозначно, поскольку он зависит от выбора калибровки .

В волновом уравнении для электромагнитного поля:

• В вакууме,$${\displaystyle ({\boldsymbol {\partial }}\cdot {\boldsymbol {\partial }})\mathbf {A} =0}$$
• С источником четырех токов и использованием условия калибровки Лоренца ,${\displaystyle ({\boldsymbol {\partial }}\cdot \mathbf {A} )=0}$$${\displaystyle ({\boldsymbol {\partial }}\cdot {\boldsymbol {\partial }})\mathbf {A} =\mu _{0}\mathbf {J} }$$

Фотонная плоская волна может быть описана четырехчастотной волной , определяемой как

$${\displaystyle \mathbf {N} =\nu \left(1,{\hat {\mathbf {n} }}\right)}$$

где ν — частота волны, а — единичный вектор в направлении распространения волны. Теперь:${\displaystyle {\hat {\mathbf {n} }}}$

$${\displaystyle \|\mathbf {N} \|=N^{\mu }N_{\mu }=\nu ^{2}\left(1-{\hat {\mathbf {n} }}\cdot {\hat {\mathbf {n} }}\right)=0}$$

поэтому четырехчастотность фотона всегда является нулевым вектором.

Величины, обратные времени t и пространству r, — это угловая частота ω и угловой волновой вектор k соответственно. Они образуют компоненты четырехволнового вектора или волнового четырехвектора :

$${\displaystyle \mathbf {K} =\left({\frac {\omega }{c}},{\vec {\mathbf {k} }}\right)=\left({\frac {\omega }{c}},{\frac {\omega }{v_{p}}}{\hat {\mathbf {n} }}\right)\,.}$$

Волновой четырехвектор имеет когерентную производную единицу обратных метров в СИ. ^[17]

Волновой пакет почти монохроматического света можно описать следующим образом:

$${\displaystyle \mathbf {K} ={\frac {2\pi }{c}}\mathbf {N} ={\frac {2\pi }{c}}\nu \left(1,{\hat {\mathbf {n} }}\right)={\frac {\omega }{c}}\left(1,{\hat {\mathbf {n} }}\right)~.}$$

Соотношения де Бройля затем показали, что четырехволновой вектор применим как к волнам материи,  так и к световым волнам: и , где ħ — постоянная Планка, деленная на 2π .$${\displaystyle \mathbf {P} =\hbar \mathbf {K} =\left({\frac {E}{c}},{\vec {p}}\right)=\hbar \left({\frac {\omega }{c}},{\vec {k}}\right)~.}$$${\displaystyle E=\hbar \omega }$${\displaystyle {\vec {p}}=\hbar {\vec {k}}}$

Квадрат нормы равен: и по соотношению де Бройля: мы имеем аналог соотношения энергии-импульса для материальных волн:$${\displaystyle \|\mathbf {K} \|^{2}=K^{\mu }K_{\mu }=\left({\frac {\omega }{c}}\right)^{2}-\mathbf {k} \cdot \mathbf {k} \,,}$$$${\displaystyle \|\mathbf {K} \|^{2}={\frac {1}{\hbar ^{2}}}\|\mathbf {P} \|^{2}=\left({\frac {m_{0}c}{\hbar }}\right)^{2}\,,}$$$${\displaystyle \left({\frac {\omega }{c}}\right)^{2}-\mathbf {k} \cdot \mathbf {k} =\left({\frac {m_{0}c}{\hbar }}\right)^{2}~.}$$

Обратите внимание, что для безмассовых частиц, в этом случае m ₀ = 0 , мы имеем: или ‖ k ‖ = ω / c  . Обратите внимание, что это согласуется с приведенным выше случаем; для фотонов с 3-волновым вектором модуля ω / c , в направлении распространения волны, определяемом единичным вектором$${\displaystyle \left({\frac {\omega }{c}}\right)^{2}=\mathbf {k} \cdot \mathbf {k} \,,}$$${\displaystyle \ {\hat {\mathbf {n} }}~.}$

В квантовой механике 4 -вероятностный ток или 4-вероятностный ток аналогичен электромагнитному 4-току : ^[18] где ρ — функция плотности вероятности, соответствующая временной компоненте, а j — вектор тока вероятности . В нерелятивистской квантовой механике этот ток всегда хорошо определен, поскольку выражения для плотности и тока положительно определены и допускают вероятностную интерпретацию. В релятивистской квантовой механике и квантовой теории поля не всегда возможно найти ток, особенно когда задействованы взаимодействия.$${\displaystyle \mathbf {J} =(\rho c,\mathbf {j} )}$$

Заменяя в четырехимпульсе энергию оператором энергии , а импульс оператором импульса , получаем четырехимпульсный оператор , используемый в релятивистских волновых уравнениях .

Четырехспин частицы определяется в системе покоя частицы как где s — псевдовектор спина . В квантовой механике не все три компонента этого вектора одновременно измеримы, только один компонент. Временной компонент равен нулю в системе покоя частицы, но не в любой другой системе. Этот компонент можно найти с помощью соответствующего преобразования Лоренца.$${\displaystyle \mathbf {S} =(0,\mathbf {s} )}$$

Квадрат нормы равен (с отрицательным знаком) квадрату величины спина, и согласно квантовой механике мы имеем$${\displaystyle \|\mathbf {S} \|^{2}=-|\mathbf {s} |^{2}=-\hbar ^{2}s(s+1)}$$

Это значение можно наблюдать и квантовать, причем s — это квантовое число спина (а не величина вектора спина).

Четырехвектор A также может быть определен с использованием матриц Паули в качестве базиса , опять же в различных эквивалентных обозначениях: ^[19] или явно: и в этой формулировке четырехвектор представлен как эрмитова матрица ( транспонирование матрицы и комплексное сопряжение матрицы оставляет ее неизменной), а не как действительный вектор-столбец или вектор-строка. Определитель матрицы является модулем четырехвектора, поэтому определитель является инвариантом:$${\displaystyle {\begin{aligned}\mathbf {A} &=\left(A^{0},\,A^{1},\,A^{2},\,A^{3}\right)\\&=A^{0}{\boldsymbol {\sigma }}_{0}+A^{1}{\boldsymbol {\sigma }}_{1}+A^{2}{\boldsymbol {\sigma }}_{2}+A^{3}{\boldsymbol {\sigma }}_{3}\\&=A^{0}{\boldsymbol {\sigma }}_{0}+A^{i}{\boldsymbol {\sigma }}_{i}\\&=A^{\alpha }{\boldsymbol {\sigma }}_{\alpha }\\\end{aligned}}}$$$${\displaystyle {\begin{aligned}\mathbf {A} &=A^{0}{\begin{pmatrix}1&0\\0&1\end{pmatrix}}+A^{1}{\begin{pmatrix}0&1\\1&0\end{pmatrix}}+A^{2}{\begin{pmatrix}0&-i\\i&0\end{pmatrix}}+A^{3}{\begin{pmatrix}1&0\\0&-1\end{pmatrix}}\\&={\begin{pmatrix}A^{0}+A^{3}&A^{1}-iA^{2}\\A^{1}+iA^{2}&A^{0}-A^{3}\end{pmatrix}}\end{aligned}}}$$$${\displaystyle {\begin{aligned}|\mathbf {A} |&={\begin{vmatrix}A^{0}+A^{3}&A^{1}-iA^{2}\\A^{1}+iA^{2}&A^{0}-A^{3}\end{vmatrix}}\\&=\left(A^{0}+A^{3}\right)\left(A^{0}-A^{3}\right)-\left(A^{1}-iA^{2}\right)\left(A^{1}+iA^{2}\right)\\&=\left(A^{0}\right)^{2}-\left(A^{1}\right)^{2}-\left(A^{2}\right)^{2}-\left(A^{3}\right)^{2}\end{aligned}}}$$

Эта идея использования матриц Паули в качестве базисных векторов применяется в алгебре физического пространства , являющейся примером алгебры Клиффорда .

В алгебре пространства-времени , другом примере алгебры Клиффорда, гамма-матрицы также могут образовывать базис . (Их также называют матрицами Дирака из-за их появления в уравнении Дирака ). Существует более одного способа выражения гамма-матриц, подробно описанного в этой основной статье.

Обозначение Фейнмана с косой чертой является сокращением для четырехвектора A, свернутого с гамма-матрицами:$${\displaystyle \mathbf {A} \!\!\!\!/=A_{\alpha }\gamma ^{\alpha }=A_{0}\gamma ^{0}+A_{1}\gamma ^{1}+A_{2}\gamma ^{2}+A_{3}\gamma ^{3}}$$

Четырех-импульс, свернутый с гамма-матрицами, является важным случаем в релятивистской квантовой механике и релятивистской квантовой теории поля . В уравнении Дирака и других релятивистских волновых уравнениях появляются члены вида:, в которых компоненты энергии E и импульса ( p _x , p _y , p _z ) заменяются соответствующими им операторами .$${\displaystyle \mathbf {P} \!\!\!\!/=P_{\alpha }\gamma ^{\alpha }=P_{0}\gamma ^{0}+P_{1}\gamma ^{1}+P_{2}\gamma ^{2}+P_{3}\gamma ^{3}={\dfrac {E}{c}}\gamma ^{0}-p_{x}\gamma ^{1}-p_{y}\gamma ^{2}-p_{z}\gamma ^{3}}$$

• Базовое введение в математику искривленного пространства-времени
• Пыль (относительность) для четырехвектора потока чисел
• пространство Минковского
• Паравектор
• Релятивистская механика
• Волновой вектор

• Риндлер, В. Введение в специальную теорию относительности (2-е изд.) (1991) Clarendon Press Oxford ISBN 0-19-853952-5