Ультрафильтр

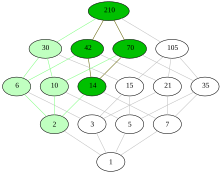
В математической области теории порядка ультрафильтр на заданном частично упорядоченном множестве (или «посете») — это определенное подмножество, а именно максимальный фильтр на , то есть собственный фильтр на , который не может быть расширен до большего собственного фильтра на${\textstyle П}$${\displaystyle P,}$ ${\displaystyle П;}$${\textstyle П}$${\displaystyle П.}$

Если — произвольное множество, его множество мощности , упорядоченное по включению множеств , всегда является булевой алгеброй и, следовательно, частично упорядоченным множеством, а ультрафильтры на обычно называются ультрафильтрами на множестве . ^{[примечание 1]} Ультрафильтр на множестве можно рассматривать как конечно-аддитивную 0-1-значную меру на . С этой точки зрения каждое подмножество из считается либо « почти всем » (имеет меру 1), либо «почти ничем» (имеет меру 0), в зависимости от того, принадлежит ли оно данному ультрафильтру или нет. ^{[1] : §4}${\displaystyle X}$ ${\displaystyle {\mathcal {P}}(X),}$${\displaystyle {\mathcal {P}}(X)}$ ${\displaystyle X}$${\displaystyle X}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle X}$

Ультрафильтры имеют множество приложений в теории множеств, теории моделей , топологии ^{[2] : 186} и комбинаторике. ^[3]

В теории порядка ультрафильтр — это подмножество частично упорядоченного множества , которое является максимальным среди всех правильных фильтров . Это подразумевает, что любой фильтр, который должным образом содержит ультрафильтр, должен быть равен всему частично упорядоченному множеству.

Формально, если — набор, то частично упорядоченный${\textstyle П}$${\displaystyle \,\leq \,}$

• подмножество называется фильтром , если${\displaystyle F\subseteq P}$${\textstyle П}$
  • ${\displaystyle F}$непусто,
  • для каждого существует некоторый элемент такой, что и и${\displaystyle x,y\in F,}$${\displaystyle z\in F}$${\displaystyle z\leq x}$${\displaystyle z\leq y,}$
  • для каждого и подразумевает, что это тоже;${\displaystyle x\in F}$${\displaystyle y\in P,}$ ${\displaystyle x\leq y}$${\displaystyle у}$${\displaystyle F}$
• собственное подмножество называется ультрафильтром , если​${\displaystyle U}$${\textstyle П}$${\textstyle П}$
  • ${\displaystyle U}$является фильтром и${\displaystyle P,}$
  • не существует подходящего фильтра , который бы правильно расширял (то есть был бы подходящим подмножеством ).${\displaystyle F}$${\textstyle П}$${\displaystyle U}$${\displaystyle U}$${\displaystyle F}$

Каждый ультрафильтр попадает ровно в одну из двух категорий: главный или свободный. Главный (или фиксированный , или тривиальный ) ультрафильтр — это фильтр, содержащий наименьший элемент . Следовательно, каждый главный ультрафильтр имеет вид для некоторого элемента заданного частично упорядоченного множества. В этом случае называется главным элементом ультрафильтра. Любой ультрафильтр, который не является главным, называется свободным (или неглавным ) ультрафильтром. Для произвольного множество является фильтром, называемым главным фильтром при ; он является главным ультрафильтром только в том случае, если он максимален.${\displaystyle F_{p}=\{x:p\leq x\}}$${\displaystyle p}$${\displaystyle p}$${\displaystyle p}$${\displaystyle F_{p}}$${\displaystyle p}$

Для ультрафильтров на множестве степеней главный ультрафильтр состоит из всех подмножеств , содержащих заданный элемент Каждый ультрафильтр на , который также является главным фильтром, имеет этот вид. ^{[2] : 187} Следовательно, ультрафильтр на является главным тогда и только тогда, когда он содержит конечное множество. ^{[примечание 2]} Если бесконечно, то ультрафильтр на является неглавным тогда и только тогда, когда он содержит фильтр Фреше коконечных подмножеств ^{[примечание 3] [4] : Предложение 3} Если конечно, то каждый ультрафильтр является главным. ^{[2] : 187} Если бесконечно, то фильтр Фреше не является ультрафильтром на множестве степеней , но является ультрафильтром на конечно-коконечной алгебре${\displaystyle {\mathcal {P}}(X),}$${\displaystyle X}$${\displaystyle x\in X.}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle U}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle X}$${\displaystyle U}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle X.}$${\displaystyle X}$${\displaystyle X}$${\displaystyle X}$${\displaystyle X.}$

Каждый фильтр на булевой алгебре (или, в более общем смысле, любое подмножество со свойством конечного пересечения ) содержится в ультрафильтре (см. лемму об ультрафильтре ), и поэтому свободные ультрафильтры существуют, но доказательства включают аксиому выбора ( AC ) в форме леммы Цорна . С другой стороны, утверждение о том, что каждый фильтр содержится в ультрафильтре, не подразумевает AC . Действительно, это эквивалентно теореме о простом идеале Буля ( BPIT ), хорошо известной промежуточной точке между аксиомами теории множеств Цермело–Френкеля ( ZF ) и теории ZF , дополненной аксиомой выбора ( ZFC ). В общем случае доказательства, включающие аксиому выбора, не дают явных примеров свободных ультрафильтров, хотя явные примеры можно найти в некоторых моделях ZFC ; например, Гёдель показал, что это можно сделать в конструируемой вселенной , где можно записать явную глобальную функцию выбора. В ZF без аксиомы выбора возможно, что каждый ультрафильтр является главным. ^[5]

Важный частный случай концепции возникает, если рассматриваемый ч.у.м. является булевой алгеброй . В этом случае ультрафильтры характеризуются тем, что содержат для каждого элемента булевой алгебры ровно один из элементов и (последний является булевым дополнением ) :${\displaystyle x}$${\displaystyle x}$${\displaystyle \lnot x}$${\displaystyle x}$

Если — булева алгебра и — правильный фильтр, то следующие утверждения эквивалентны:${\textstyle П}$${\displaystyle F}$${\displaystyle P,}$

1. ${\displaystyle F}$является ультрафильтром на${\displaystyle P,}$
2. ${\displaystyle F}$является основным фильтром${\displaystyle P,}$
3. для каждого или ( ) ^{[2] : 186}${\displaystyle x\in P,}$${\displaystyle x\in F}$${\displaystyle \lnot x}$${\displaystyle \in Ф.}$

Доказательство того, что 1. и 2. эквивалентны, также приведено в (Беррис, Санкаппанавар, 2012, Следствие 3.13, стр. 133). ^[6]

Более того, ультрафильтры на булевой алгебре могут быть связаны с максимальными идеалами и гомоморфизмами на 2-элементной булевой алгебре {true, false} (также известные как 2-значные морфизмы ) следующим образом:

• Если задан гомоморфизм булевой алгебры на {true, false}, то обратный образ «true» является ультрафильтром, а обратный образ «false» является максимальным идеалом.
• Если задан максимальный идеал булевой алгебры, его дополнение является ультрафильтром, и существует единственный гомоморфизм на {true, false}, переводящий максимальный идеал в «false».
• Если задан ультрафильтр на булевой алгебре, его дополнение является максимальным идеалом, и существует единственный гомоморфизм на {true, false}, переводящий ультрафильтр в «true». ^{[ требуется ссылка ]}

При наличии произвольного множества его множество мощности , упорядоченное включением множеств , всегда является булевой алгеброй; следовательно, применяются результаты предыдущего раздела. (Ультра)фильтр на часто называют просто "(ультра)фильтр на ". ^{[примечание 1]} При наличии произвольного множества ультрафильтр на — это множество, состоящее из подмножеств таких, что:${\displaystyle X,}$ ${\displaystyle {\mathcal {P}}(X),}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle X}$${\displaystyle X,}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle {\mathcal {U}}}$${\displaystyle X}$

1. Пустое множество не является элементом .${\displaystyle {\mathcal {U}}}$
2. Если является элементом , то таковым является и каждое надмножество .${\displaystyle А}$${\displaystyle {\mathcal {U}}}$${\displaystyle B\supset A}$
3. Если и являются элементами , то также является и пересечение .${\displaystyle А}$${\displaystyle Б}$${\displaystyle {\mathcal {U}}}$ ${\displaystyle A\cap B}$
4. Если является подмножеством , то либо ^{[примечание 4]} , либо его дополнение является элементом .${\displaystyle А}$${\displaystyle X,}$ ${\displaystyle А}$${\displaystyle X\setminus A}$${\displaystyle {\mathcal {U}}}$

Эквивалентно, семейство подмножеств является ультрафильтром тогда и только тогда, когда для любого конечного набора подмножеств , существует такое , что где является главным ультрафильтром, затравленным . Другими словами, ультрафильтр можно рассматривать как семейство множеств, которое «локально» напоминает главный ультрафильтр. ^{[ необходима цитата ]}${\displaystyle {\mathcal {U}}}$${\displaystyle X}$${\displaystyle {\mathcal {F}}}$${\displaystyle X}$${\displaystyle x\in X}$${\displaystyle {\mathcal {U}}\cap {\mathcal {F}}=F_{x}\cap {\mathcal {F}}}$${\displaystyle F_{x}=\{Y\subseteq X:x\in Y\}}$${\displaystyle x}$

Эквивалентной формой данного является 2-значный морфизм , функция на , определенная как если является элементом и в противном случае. Тогда конечно аддитивно , и, следовательно, содержание на и каждое свойство элементов либо истинно почти всюду , либо ложно почти всюду. Однако, обычно не является счетно-аддитивным , и, следовательно, не определяет меру в обычном смысле.${\displaystyle {\mathcal {U}}}$${\displaystyle м}$${\displaystyle {\mathcal {P}}(X)}$${\displaystyle m(A)=1}$${\displaystyle А}$${\displaystyle {\mathcal {U}}}$${\displaystyle m(A)=0}$${\displaystyle м}$${\displaystyle {\mathcal {P}}(X),}$${\displaystyle X}$${\displaystyle м}$

Для фильтра , который не является ультрафильтром, можно определить if и if , оставив неопределенным в других местах. ^[1]${\displaystyle {\mathcal {F}}}$${\displaystyle m(A)=1}$${\displaystyle A\in {\mathcal {F}}}$${\displaystyle m(A)=0}$${\displaystyle X\setminus A\in {\mathcal {F}},}$${\displaystyle м}$

Ультрафильтры на множествах мощности полезны в топологии , особенно в отношении компактных хаусдорфовых пространств, и в теории моделей при построении ультрапроизведений и ультрастепеней . Каждый ультрафильтр на компактном хаусдорфовом пространстве сходится ровно к одной точке. Аналогично, ультрафильтры на булевых алгебрах играют центральную роль в теореме Стоуна о представлении . В теории множеств ультрафильтры используются для того, чтобы показать, что аксиома конструктивности несовместима с существованием измеримого кардинала κ . Это доказывается путем взятия ультрастепени теоретико-множественной вселенной по модулю κ -полного, неглавного ультрафильтра. ^[7]

Множество всех ультрафильтров частично упорядоченного множества может быть топологизировано естественным образом, что на самом деле тесно связано с вышеупомянутой теоремой о представлении. Для любого элемента из , пусть Это наиболее полезно, когда снова является булевой алгеброй, поскольку в этой ситуации множество всех является базой для компактной хаусдорфовой топологии на . В частности, при рассмотрении ультрафильтров на мощностном множестве результирующее топологическое пространство является компактификацией Стоуна–Чеха дискретного пространства мощности${\displaystyle G}$${\textstyle П}$${\displaystyle x}$${\textstyle П}$${\displaystyle D_{x}=\left\{U\in G:x\in U\right\}.}$${\textstyle П}$${\displaystyle D_{x}}$${\displaystyle G}$${\displaystyle {\mathcal {P}}(S)}$${\displaystyle |С|.}$

Конструкция ультрапроизведения в теории моделей использует ультрафильтры для создания новой модели, начиная с последовательности -индексированных моделей; например, теорема о компактности может быть доказана таким образом. В частном случае ультрастепеней получаются элементарные расширения структур. Например, в нестандартном анализе гипердействительные числа могут быть построены как ультрапроизведение действительных чисел , расширяя область дискурса от действительных чисел до последовательностей действительных чисел. Это пространство последовательностей рассматривается как надмножество действительных чисел путем идентификации каждого действительного числа с соответствующей постоянной последовательностью. Чтобы расширить знакомые функции и отношения (например, + и <) от действительных чисел до гипердействительных, естественная идея состоит в том, чтобы определить их поточечно. Но это приведет к потере важных логических свойств действительных чисел; например, поточечное < не является полным упорядочением. Поэтому вместо этого функции и отношения определяются « поточечно по модулю » , где — ультрафильтр на индексном множестве последовательностей; по теореме Лося это сохраняет все свойства вещественных чисел, которые могут быть сформулированы в логике первого порядка . Если является неглавным, то полученное таким образом расширение является нетривиальным.${\displaystyle X}$${\displaystyle U}$${\displaystyle U}$${\displaystyle U}$

В геометрической теории групп неглавные ультрафильтры используются для определения асимптотического конуса группы. Эта конструкция дает строгий способ рассмотрения группы из бесконечности , то есть крупномасштабной геометрии группы. Асимптотические конусы являются частными примерами ультрапределов метрических пространств .

Онтологическое доказательство существования Бога Гёделем использует в качестве аксиомы то, что множество всех «положительных свойств» является ультрафильтром.

В теории общественного выбора неглавные ультрафильтры используются для определения правила (называемого функцией общественного благосостояния ) для агрегирования предпочтений бесконечного числа индивидов. Вопреки теореме Эрроу о невозможности для конечного числа индивидов, такое правило удовлетворяет условиям (свойствам), которые предлагает Эрроу (например, Кирман и Зондерманн, 1972). ^[8] Михара (1997, ^[9] 1999) ^[10] показывает, однако, что такие правила на практике представляют ограниченный интерес для социальных ученых, поскольку они неалгоритмичны или невычислимы.

• Фильтр (математика)  — в математике особое подмножество частично упорядоченного множества.
• Фильтр (теория множеств)  – Семейство множеств, представляющих «большие» множества
• Фильтры в топологии  – использование фильтров для описания и характеристики всех основных топологических понятий и результатов.
• Лемма об ультрафильтре  – Максимальный собственный фильтрСтраницы, отображающие краткие описания целей перенаправления
• Универсальная сеть  – обобщение последовательности точек.Страницы, отображающие краткие описания целей перенаправления

• Архангельский, Александр Владимирович ; Пономарев, В.И. (1984). Основы общей топологии: задачи и упражнения . Математика и ее приложения. Т. 13. Дордрехт Бостон: Д. Рейдель . ISBN 978-90-277-1355-1. OCLC  9944489.
• Бурбаки, Николя (1989) [1966]. Общая топология: главы 1–4 [ Общая топология ]. Элементы математики . Берлин, Нью-Йорк: Springer Science & Business Media. ISBN 978-3-540-64241-1. OCLC  18588129.
• Диксмье, Жак (1984). Общая топология . Бакалаврские тексты по математике. Перевод Бербериана, SK New York: Springer-Verlag . ISBN 978-0-387-90972-1. OCLC  10277303.
• Dolecki, Szymon; Mynard, Frédéric (2016). Convergence Foundations Of Topology . Нью-Джерси: World Scientific Publishing Company. ISBN 978-981-4571-52-4. OCLC  945169917.
• Дугунджи, Джеймс (1966). Топология . Бостон: Аллин и Бэкон. ISBN 978-0-697-06889-7. OCLC  395340485.
• Часар, Акош (1978). Общая топология . Перевод Часара, Клары. Бристоль, Англия: ISBN Adam Hilger Ltd. 0-85274-275-4. OCLC  4146011.
• Jech, Thomas (2006). Теория множеств: издание третьего тысячелетия, исправленное и расширенное . Берлин Нью-Йорк: Springer Science & Business Media. ISBN 978-3-540-44085-7. OCLC  50422939.
• Джоши, К. Д. (1983). Введение в общую топологию . Нью-Йорк: John Wiley and Sons Ltd. ISBN 978-0-85226-444-7. OCLC  9218750.
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC  144216834.
• Шехтер, Эрик (1996). Справочник по анализу и его основам . Сан-Диего, Калифорния: Academic Press. ISBN 978-0-12-622760-4. OCLC  175294365.
• Шуберт, Хорст (1968). Топология . Лондон: Macdonald & Co. ISBN 978-0-356-02077-8. OCLC  463753.

• Comfort, WW (1977). «Ультрафильтры: некоторые старые и некоторые новые результаты». Бюллетень Американского математического общества . 83 (4): 417–455. doi : 10.1090/S0002-9904-1977-14316-4 . ISSN  0002-9904. MR  0454893.
• Comfort, WW; Negrepontis, S. (1974), Теория ультрафильтров , Берлин, Нью-Йорк: Springer-Verlag , MR  0396267
• Ультрафильтр в лаборатории n
• «Математическая логика 15, Теорема об ультрафильтре» на YouTube