Элементарный поток

В более широком контексте уравнений Навье-Стокса (и особенно в контексте теории потенциала ) элементарные потоки являются базовыми потоками, которые можно комбинировать, используя различные методы, для построения более сложных потоков. В этой статье термин «поток» используется взаимозаменяемо с термином «решение» по историческим причинам.

Методы, используемые для создания более сложных решений, могут быть, например, суперпозицией , такими методами, как топология или рассмотрением их как локальных решений на определенной окрестности, подобласти или пограничном слое и их склеиванием. Элементарные потоки можно считать основными строительными блоками ( фундаментальные решения , локальные решения и солитоны ) различных типов уравнений, полученных из уравнений Навье-Стокса. Некоторые потоки отражают определенные ограничения, такие как несжимаемые или безвихревые потоки, или и то, и другое, как в случае потенциального потока , а некоторые потоки могут быть ограничены случаем двух измерений. [1]

Из-за связи между динамикой жидкости и теорией поля элементарные потоки имеют отношение не только к аэродинамике , но и ко всей теории поля в целом. Если рассматривать это в перспективе, пограничные слои можно интерпретировать как топологические дефекты на общих многообразиях , и, рассматривая аналогии с динамикой жидкости и предельные случаи в электромагнетизме , квантовой механике и общей теории относительности, можно увидеть, как все эти решения лежат в основе последних разработок в теоретической физике, таких как дуальность ads/cft, модель SYK, физика нематических жидкостей, сильно коррелированных систем и даже кварк-глюонной плазмы.

Двумерный равномерный поток

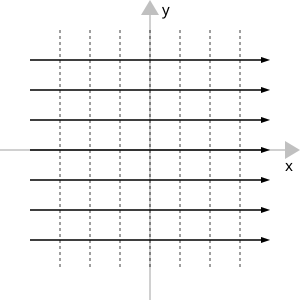
Униформа
Потенциальные линии потока для идеального равномерного потока

Для установившегося, пространственно однородного течения жидкости в плоскости xy вектор скорости равен

v = v 0 cos ⁡ ( θ 0 ) e x + v 0 sin ⁡ ( θ 0 ) e y {\displaystyle \mathbf {v} =v_{0}\cos(\theta _{0})\,\mathbf {e} _{x}+v_{0}\sin(\theta _{0})\,\mathbf {e} _{y}}

где

v 0 {\displaystyle v_{0}} — абсолютная величина скорости (т.е. ); v 0 = | v | {\displaystyle v_{0}=|\mathbf {v} |}
θ 0 {\displaystyle \theta _{0}} — угол, который вектор скорости образует с положительной осью x ( положителен для углов, измеренных против часовой стрелки от положительной оси x ); и θ 0 {\displaystyle \theta _{0}}
e x {\displaystyle \mathbf {e} _{x}} и являются единичными базисными векторами системы координат xy . e y {\displaystyle \mathbf {e} _{y}}

Поскольку этот поток несжимаем (т.е. ) и двумерен, его скорость можно выразить через функцию тока , : ∇ ⋅ v = 0 {\displaystyle \nabla \cdot \mathbf {v} =0} ψ {\displaystyle \psi }

v x = ∂ ψ ∂ y {\displaystyle v_{x}={\frac {\partial \psi }{\partial y}}}
v y = − ∂ ψ ∂ x {\displaystyle v_{y}=-{\frac {\partial \psi }{\partial x}}}

где

ψ = ψ 0 − v 0 sin ⁡ ( θ 0 ) x + v 0 cos ⁡ ( θ 0 ) y {\displaystyle \psi =\psi _{0}-v_{0}\sin(\theta _{0})\,x+v_{0}\cos(\theta _{0})\,y}

и является константой. ψ 0 {\displaystyle \psi _{0}}

В цилиндрических координатах:

v r = − 1 r ∂ ψ ∂ θ {\displaystyle v_{r}=-{\frac {1}{r}}{\frac {\partial \psi }{\partial \theta }}}
v θ = ∂ ψ ∂ r {\displaystyle v_{\theta }={\frac {\partial \psi }{\partial r}}}

и

ψ = ψ 0 + v 0 r sin ⁡ ( θ − θ 0 ) {\displaystyle \psi =\psi _{0}+v_{0}\,r\sin(\theta -\theta _{0})}

Этот поток является безвихревым (т.е. ), поэтому его скорость можно выразить через потенциальную функцию : ∇ × v = 0 {\displaystyle \nabla \times \mathbf {v} =\mathbf {0} } ϕ {\displaystyle \phi }

v x = − ∂ ϕ ∂ x {\displaystyle v_{x}=-{\frac {\partial \phi }{\partial x}}}
v y = − ∂ ϕ ∂ y {\displaystyle v_{y}=-{\frac {\partial \phi }{\partial y}}}

где

ϕ = ϕ 0 − v 0 cos ⁡ ( θ 0 ) x − v 0 sin ⁡ ( θ 0 ) y {\displaystyle \phi =\phi _{0}-v_{0}\cos(\theta _{0})\,x-v_{0}\sin(\theta _{0})\,y}

и является константой. ϕ 0 {\displaystyle \phi _{0}}

В цилиндрических координатах

v r = ∂ ϕ ∂ r {\displaystyle v_{r}={\frac {\partial \phi }{\partial r}}}
v θ = 1 r ∂ ϕ ∂ θ {\displaystyle v_{\theta }={\frac {1}{r}}{\frac {\partial \phi }{\partial \theta }}}
ϕ = ϕ 0 − v 0 r cos ⁡ ( θ − θ 0 ) {\displaystyle \phi =\phi _{0}-v_{0}\,r\cos(\theta -\theta _{0})}

Двумерный линейный источник

Точка-источник
Потенциальные линии потока для идеального линейного источника

Случай вертикальной линии, испускающей с фиксированной скоростью постоянное количество жидкости Q на единицу длины, является линейным источником. Задача имеет цилиндрическую симметрию и может рассматриваться в двух измерениях на ортогональной плоскости.

Линейные источники и линейные стоки (ниже) являются важными элементарными потоками, поскольку они играют роль монополя для несжимаемых жидкостей (которые также можно считать примерами соленоидальных полей , т.е. полей без дивергенции). Общие модели потока также могут быть разложены в терминах мультипольных расширений , таким же образом, как для электрических и магнитных полей, где монополь по существу является первым нетривиальным (например, постоянным) членом расширения.

Этот режим течения также является безвихревым и несжимаемым.

Это характеризуется цилиндрической симметрией:

v = v r ( r ) e r {\displaystyle \mathbf {v} =v_{r}(r)\mathbf {e} _{r}}

Где общий исходящий поток постоянен

∫ S v ⋅ d S = ∫ 0 2 π ( v r ( r ) e r ) ⋅ ( e r r d θ ) = 2 π r v r ( r ) = Q {\displaystyle \int _{S}\mathbf {v} \cdot d\mathbf {S} =\int _{0}^{2\pi }(v_{r}(r)\,\mathbf {e} _{r})\cdot (\mathbf {e} _{r}\,r\,d\theta )=\!2\pi \,r\,v_{r}(r)=Q}

Поэтому,

v r = Q 2 π r {\displaystyle v_{r}={\frac {Q}{2\pi r}}}

Это выводится из функции потока

ψ ( r , θ ) = − Q 2 π θ {\displaystyle \psi (r,\theta )=-{\frac {Q}{2\pi }}\theta }

или из потенциальной функции

ϕ ( r , θ ) = − Q 2 π ln ⁡ r {\displaystyle \phi (r,\theta )=-{\frac {Q}{2\pi }}\ln r}

Двумерная линейная раковина

Случай вертикальной линии, поглощающей с фиксированной скоростью постоянное количество жидкости Q на единицу длины, является стоком линии. Все то же самое, что и в случае источника линии, за исключением знака «минус».

v r = − Q 2 π r {\displaystyle v_{r}=-{\frac {Q}{2\pi r}}}

Это выводится из функции потока

ψ ( r , θ ) = Q 2 π θ {\displaystyle \psi (r,\theta )={\frac {Q}{2\pi }}\theta }

или из потенциальной функции

ϕ ( r , θ ) = Q 2 π ln ⁡ r {\displaystyle \phi (r,\theta )={\frac {Q}{2\pi }}\ln r}

Учитывая, что два результата одинаковы, за исключением знака минус, мы можем прозрачно трактовать как линейные источники, так и линейные стоки с одинаковыми функциями потока и потенциала, позволяя Q принимать как положительные , так и отрицательные значения и включая знак минус в определение Q.

Двумерный дублетный или дипольный линейный источник

Потенциальные линии тока для идеальной дублетной или дипольной линии

Если мы рассмотрим линейный источник и линейный сток на расстоянии d, мы можем повторно использовать результаты, приведенные выше, и функция потока будет иметь вид

ψ ( r ) = ψ Q ( r − d / 2 ) − ψ Q ( r + d / 2 )   ≃ d ⋅ ∇ ψ Q ( r ) {\displaystyle \psi (\mathbf {r} )=\psi _{Q}(\mathbf {r} -\mathbf {d} /2)-\psi _{Q}(\mathbf {r} +\mathbf {d} /2)\ \simeq \mathbf {d} \cdot \nabla \psi _{Q}(\mathbf {r} )}

Последнее приближение — к первому порядку по d.

Данный

d = d [ cos ⁡ ( θ 0 ) e x + sin ⁡ ( θ 0 ) e y ] = d [ cos ⁡ ( θ − θ 0 ) e r + sin ⁡ ( θ − θ 0 ) e θ ] {\displaystyle \mathbf {d} =d[\cos(\theta _{0})\mathbf {e} _{x}+\sin(\theta _{0})\mathbf {e} _{y}]=d[\cos(\theta -\theta _{0})\mathbf {e} _{r}+\sin(\theta -\theta _{0})\mathbf {e} _{\theta }]}

Остается

ψ ( r , θ ) = − Q d 2 π sin ⁡ ( θ − θ 0 ) r {\displaystyle \psi (r,\theta )=-{\frac {Qd}{2\pi }}{\frac {\sin(\theta -\theta _{0})}{r}}}

Скорость тогда равна

v r ( r , θ ) = Q d 2 π cos ⁡ ( θ − θ 0 ) r 2 {\displaystyle v_{r}(r,\theta )={\frac {Qd}{2\pi }}{\frac {\cos(\theta -\theta _{0})}{r^{2}}}}
v θ ( r , θ ) = Q d 2 π sin ⁡ ( θ − θ 0 ) r 2 {\displaystyle v_{\theta }(r,\theta )={\frac {Qd}{2\pi }}{\frac {\sin(\theta -\theta _{0})}{r^{2}}}}

И потенциал вместо этого

ϕ ( r , θ ) = Q d 2 π cos ⁡ ( θ − θ 0 ) r {\displaystyle \phi (r,\theta )={\frac {Qd}{2\pi }}{\frac {\cos(\theta -\theta _{0})}{r}}}

Двумерная вихревая линия

Потенциальные линии тока для идеальной вихревой линии

Это случай вихревой нити, вращающейся с постоянной скоростью, имеет место цилиндрическая симметрия, и задачу можно решить в ортогональной плоскости.

Вихревые линии, как и в случае линейных источников, играют роль монополей для безвихревых потоков .

В этом случае поток также является как безвихревым , так и несжимаемым , и, следовательно, представляет собой случай потенциального потока .

Это характеризуется цилиндрической симметрией:

v = v θ ( r ) e θ {\displaystyle \mathbf {v} =v_{\theta }(r)\,\mathbf {e} _{\theta }}

Где общая циркуляция постоянна для каждой замкнутой линии вокруг центрального вихря

∮ v ⋅ d s = ∫ 0 2 π ( v θ ( r ) e θ ) ⋅ ( e θ r d θ ) = 2 π r v θ ( r ) = Γ {\displaystyle \oint \mathbf {v} \cdot d\mathbf {s} =\int _{0}^{2\pi }(v_{\theta }(r)\,\mathbf {e} _{\theta })\cdot (\mathbf {e} _{\theta }\,r\,d\theta )=\!2\pi \,r\,v_{\theta }(r)=\Gamma }

и равен нулю для любой линии, не включая вихрь.

Поэтому,

v θ = Γ 2 π r {\displaystyle v_{\theta }={\frac {\Gamma }{2\pi r}}}

Это выводится из функции потока

ψ ( r , θ ) = Γ 2 π ln ⁡ r {\displaystyle \psi (r,\theta )={\frac {\Gamma }{2\pi }}\ln r}

или из потенциальной функции

ϕ ( r , θ ) = − Γ 2 π θ {\displaystyle \phi (r,\theta )=-{\frac {\Gamma }{2\pi }}\theta }

Что является двойственным к предыдущему случаю линейного источника

Общий двумерный потенциальный поток

Для несжимаемого двумерного потока, который также является безвихревым, имеем:

∇ 2 ψ = 0 {\displaystyle \nabla ^{2}\psi =0}

Который находится в цилиндрических координатах [2]

1 r ∂ ∂ r ( r ∂ ψ ∂ r ) + 1 r 2 ∂ 2 ψ ∂ θ 2 = 0 {\displaystyle {\frac {1}{r}}{\frac {\partial }{\partial r}}\left(r{\frac {\partial \psi }{\partial r}}\right)+{\frac {1}{r^{2}}}{\frac {\partial ^{2}\psi }{\partial \theta ^{2}}}=0}

Ищем решение с разделенными переменными:

ψ ( r , θ ) = R ( r ) Θ ( θ ) {\displaystyle \psi (r,\theta )=R(r)\Theta (\theta )}

что дает

r R ( r ) d d r ( r d R ( r ) d r ) = − 1 Θ ( θ ) d 2 Θ ( θ ) d θ 2 {\displaystyle {\frac {r}{R(r)}}{\frac {d}{dr}}\left(r{\frac {dR(r)}{dr}}\right)=-{\frac {1}{\Theta (\theta )}}{\frac {d^{2}\Theta (\theta )}{d\theta ^{2}}}}

Учитывая, что левая часть зависит только от r , а правая часть зависит только от , обе части должны быть равны константе, независимой от r и . Константа должна быть положительной [ необходимо разъяснение ] . Следовательно, θ {\displaystyle \theta } θ {\displaystyle \theta }

r d d r ( r d d r R ( r ) ) = m 2 R ( r ) {\displaystyle r{\frac {d}{dr}}\left(r{\frac {d}{dr}}R(r)\right)=m^{2}R(r)}
d 2 Θ ( θ ) d θ 2 = − m 2 Θ ( θ ) {\displaystyle {\frac {d^{2}\Theta (\theta )}{d\theta ^{2}}}=-m^{2}\Theta (\theta )}

Решением второго уравнения является линейная комбинация и Для того чтобы иметь однозначную скорость (а также однозначную функцию тока), m должно быть положительным целым числом. e i m θ {\displaystyle e^{im\theta }} e − i m θ {\displaystyle e^{-im\theta }}

поэтому наиболее общее решение дается следующим образом:

ψ = α 0 + β 0 ln ⁡ r + ∑ m > 0 ( α m r m + β m r − m ) sin ⁡ [ m ( θ − θ m ) ] {\displaystyle \psi =\alpha _{0}+\beta _{0}\ln r+\sum _{m>0}{\left(\alpha _{m}r^{m}+\beta _{m}r^{-m}\right)\sin {[m(\theta -\theta _{m})]}}}

Потенциал вместо этого определяется как

ϕ = α 0 − β 0 θ + ∑ m > ⁡ 0 ( α m r m − β m r − m ) cos ⁡ [ m ( θ − θ m ) ] {\displaystyle \phi =\alpha _{0}-\beta _{0}\theta +\sum _{m\mathop {>} 0}{(\alpha _{m}r^{m}-\beta _{m}r^{-m})\cos {[m(\theta -\theta _{m})]}}}

Ссылки

  • Фицпатрик, Ричард (2017), Теоретическая гидродинамика, наука об ИОП, ISBN 978-0-7503-1554-8
  • Фабер, TE (1995), Гидродинамика для физиков, Cambridge University Press, ISBN 9780511806735
Специфический
  1. ^ Оливер, Дэвид (2013-03-14). Лохматый конь физики: математическая красота в физическом мире. Springer Science & Business Media. ISBN 978-1-4757-4347-0.
  2. ^ Оператор Лапласа

Дальнейшее чтение

Retrieved from "https://en.wikipedia.org/w/index.php?title=Elementary_flow&oldid=1240233890"