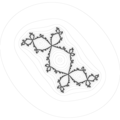
Кролик Дуади

Кролик Дуади — это фрактал, полученный из множества Жюлиа функции , когда параметр находится вблизи центра одной из трех периодов множества Мандельброта для комплексного квадратичного отображения . ${\textstyle f_{c}(z)=z^{2}+c}$ ${\displaystyle с}$

Назван в честь французского математика Адриена Дуади .

Кролик Дуади генерируется путем итерации карты множества Мандельброта на комплексной плоскости , где параметр зафиксирован так, чтобы лежать в одном из двух периодов трех луковиц от основной кардиоиды и располагаться на плоскости. Полученное изображение можно раскрасить, сопоставив каждому пикселю начальное значение и вычислив количество итераций, требуемых до того, как значение выйдет за пределы ограниченной области, после чего оно будет стремиться к бесконечности .${\displaystyle z_{n+1}=z_{n}^{2}+c}$${\displaystyle с}$${\displaystyle z}$${\displaystyle z_{0}}$${\displaystyle z_{n}}$

Его также можно описать с помощью логистической картографической формы комплексного квадратичного отображения , а именно:

${\displaystyle z_{n+1}={\mathcal {M}}z_{n}:=\gamma z_{n}\left(1-z_{n}\right).}$

что эквивалентно

${\displaystyle w_{n+1}=w_{n}^{2}+c}$.

Независимо от конкретной используемой итерации, заполненный набор Жюлиа , связанный с заданным значением (или ), состоит из всех начальных точек (или ), для которых итерация остается ограниченной. Тогда набор Мандельброта состоит из тех значений (или ), для которых связанный заполненный набор Жюлиа связан. Набор Мандельброта можно рассматривать относительно либо , либо .${\displaystyle \гамма}$${\displaystyle \мю}$${\displaystyle z_{0}}$${\displaystyle w_{0}}$${\displaystyle \гамма}$${\displaystyle \мю}$${\displaystyle \гамма}$${\displaystyle \мю}$

Заметив, что инвариантно относительно замены , множество Мандельброта относительно имеет дополнительную горизонтальную симметрию. Поскольку и являются аффинными преобразованиями друг друга, или, более конкретно, преобразованием подобия, состоящим только из масштабирования, вращения и переноса, заполненные множества Жюлиа выглядят одинаково для любой формы итерации, приведенной выше.${\displaystyle \мю}$${\displaystyle \gamma \to 2-\gamma }$${\displaystyle \гамма}$${\displaystyle z}$${\displaystyle w}$

Вы также можете описать кролика Дуади, используя множество Мандельброта относительно , ​​как показано на графике выше. На этом рисунке множество Мандельброта поверхностно выглядит как два единичных диска, расположенных спина к спине, с ростками или почками , такими как ростки в положениях один и пять часов на правом диске или ростки в положениях семь и одиннадцать часов на левом диске. Когда находится в пределах одного из этих четырех ростков, соответствующее заполненное множество Жюлиа в плоскости отображения называется кроликом Дуади. Для этих значений можно показать, что имеет и одну другую точку как нестабильные (отталкивающие) неподвижные точки и как притягивающую неподвижную точку. Более того, на карте есть три притягивающие неподвижные точки. Кролик Дуади состоит из трех притягивающих неподвижных точек , и и их бассейнов притяжения.${\displaystyle \гамма}$${\displaystyle \гамма}$${\displaystyle \гамма}$${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=\infty}$${\displaystyle {\mathcal {M}}^{3}}$${\displaystyle z_{1}}$${\displaystyle z_{2}}$${\displaystyle z_{3}}$

Например, на рисунке 4 показан кролик Дуади на плоскости, когда , точка в пятичасовом отростке правого диска. Для этого значения , карта имеет отталкивающие неподвижные точки и . Три притягивающие неподвижные точки (также называемые неподвижными точками периода три) имеют местоположения${\displaystyle z}$${\displaystyle \гамма =\гамма _{D}=2,55268-0,959456i}$${\displaystyle \гамма}$${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=.656747-.129015i}$${\displaystyle {\mathcal {M}}^{3}}$

${\displaystyle {\begin{aligned}z_{1}&=0,499997032420304-(1,221880225696050\times 10^{-6})i{\;}{\;}{\mathrm {(красный)} },\\z_{2}&=0,638169999974373-(0,239864000011495)i{\;}{\;}{\mathrm {(зеленый)} },\\z_{3}&=0,799901291393262-(0,107547238170383)i{\;}{\;}{\mathrm {(желтый)} }.\end{aligned}}}$

Красные, зеленые и желтые точки лежат в бассейнах , и , соответственно . Белые точки лежат в бассейне .${\displaystyle B(z_{1})}$${\displaystyle B(z_{2})}$${\displaystyle B(z_{3})}$${\displaystyle {\mathcal {M}}^{3}}$${\displaystyle B(\infty)}$${\displaystyle {\mathcal {M}}}$

Действие на эти неподвижные точки задается соотношениями , , и .${\displaystyle {\mathcal {M}}}$${\displaystyle {\mathcal {M}}z_{1}=z_{2}}$${\displaystyle {\mathcal {M}}z_{2}=z_{3}}$${\displaystyle {\mathcal {M}}z_{3}=z_{1}}$

Соответствующие этим соотношениям результаты

${\displaystyle {\begin{aligned}{\mathcal {M}}B(z_{1})&=B(z_{2}){\;}{\mathrm {or} {\;}{\mathcal {M}}{\;}{\mathrm {red} }\subseteq {\mathrm {green} },\\{\mathcal {M}}B(z_{2})&=B(z_{3}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm { green} }\subseteq {\mathrm {yellow} },\\{\mathcal {M}}B(z_{3})&=B(z_{1}){\;}{\mathrm {or} }{\;}{\mathcal {M}}{\;}{\mathrm {yellow} }\subseteq {\mathrm {red} }.\end{выровнено}}}$

В качестве второго примера на рисунке 5 показан кролик Дуади , когда точка в одиннадцатичасовом ростке на левом диске ( инвариантна относительно этого преобразования). Этот кролик более симметричен на плоскости. Тогда неподвижные точки периода три расположены в${\displaystyle \gamma =2-\gamma _{D}=-.55268+.959456i}$${\displaystyle \mu }$

${\displaystyle {\begin{aligned}z_{1}&=0.500003730675024+(6.968273875812428\times 10^{-6})i{\;}{\;}({\mathrm {red} }),\\z_{2}&=-0.138169999969259+(0.239864000061970)i{\;}{\;}({\mathrm {green} }),\\z_{3}&=-0.238618870661709-(0.264884797354373)i{\;}{\;}({\mathrm {yellow} }).\end{aligned}}}$

Отталкивающие неподвижные точки самого себя расположены в и . Три основных лепестка слева, которые содержат период - три неподвижные точки , , и , встречаются в неподвижной точке , а их аналоги справа встречаются в точке . Можно показать, что эффект на точки вблизи начала координат состоит из вращения против часовой стрелки вокруг начала координат , или очень близкого к , за которым следует масштабирование (расширение) с коэффициентом .${\displaystyle {\mathcal {M}}}$${\displaystyle z=0}$${\displaystyle z=1.450795+0.7825835i}$${\displaystyle z_{1}}$${\displaystyle z_{2}}$${\displaystyle z_{3}}$${\displaystyle z=0}$${\displaystyle z=1}$${\displaystyle {\mathcal {M}}}$${\displaystyle \arg(\gamma )}$${\displaystyle 120^{\circ }}$${\displaystyle |\gamma |=1.1072538}$

Скрученный кролик [ ^1] ​​— это композиция многочлена кролика со степенями скручиваний Дена вокруг его ушей. ^[2]${\displaystyle n}$

Кораббит — это симметричное изображение кролика. Здесь параметр . Это один из 2 других полиномов , индуцирующих ту же перестановку их посткритического множества — кролика.${\displaystyle c\approx -0.1226-0.7449i}$

Множество Жюлиа не имеет прямого аналога в трех измерениях.

Кватернионное множество Жюлиа с параметрами и сечением в плоскости. Кролик Дуади виден в сечении.${\displaystyle c=-0.123+0.745i}$${\displaystyle xy}$

Небольшая встроенная гомеоморфная копия кролика в центре множества Жюлиа ^[3]

Толстый кролик или пухлый кролик имеет c в корне 1/3- конечности множества Мандельброта . Он имеет параболическую неподвижную точку с 3 лепестками. ^[4]

• 
  Толстый кролик
• 
  Параболическая шахматная доска

В общем случае кролик для четвертой луковицы основной кардиоиды будет иметь уши ^[5]. Например, кролик для четвертой луковицы периода имеет три уха.${\displaystyle period-(n+1)}$${\displaystyle n}$

Встревоженный кролик ^[6]

• Встревоженный кролик
• 
  Встревоженный кролик
• 
  Взволнованный кролик зум

В начале 1980-х годов Хаббард сформулировал так называемую задачу о скрученном кролике, задачу полиномиальной классификации. Цель состоит в том, чтобы определить типы эквивалентности Терстона ^{[ необходимо определение ]} функций комплексных чисел , которые обычно не задаются формулой (они называются топологическими полиномами): ^[7]

• дан топологический квадратичный многочлен, точка ветвления которого является периодической с периодом три, определение того, какому квадратичному многочлену он эквивалентен по Терстону
• определение класса эквивалентности скрученных кроликов, т.е. композиции многочлена кролика с n-ными степенями скручиваний Дена вокруг его ушей.

Первоначально задача была решена Лораном Бартольди и Владимиром Некрашевичем ^[8] с использованием итерированных монодромных групп . Обобщение задачи на случай, когда число посткритических точек произвольно велико, также было решено. ^[9]

• 
  Уровни серого цвета указывают скорость сходимости к бесконечности или к притягивающему циклу.
• 
  Границы множеств уровней
• 
  Двоичное разложение
• 
• 
  С позвоночником
• 
  С внешними лучами
• 
  Кролик породы Дуади Multibrot-4
• 
  Кролик Дуади на красном фоне
• 
  Цепочка кроликов Дуади

• Кривая дракона
• кольцо Германа
• диск Сигеля

• Вайсштейн, Эрик В. «Фрактал кролика Дуади». MathWorld .
• Драгт, А. «Методы Ли для нелинейной динамики с приложениями к физике ускорителей».
• Адриен Дуади: La dynamic du lapin (1996) - видео на YouTube

В данной статье использованы материалы Douady Rabbit с сайта PlanetMath , лицензированные по лицензии Creative Commons Attribution/Share-Alike License .