Кубический корень
В математике кубический корень числа x — это число y, такое что y 3 = x . Все ненулевые действительные числа имеют ровно один действительный кубический корень и пару комплексно-сопряженных кубических корней, а все ненулевые комплексные числа имеют три различных комплексных кубических корня. Например, действительный кубический корень числа 8 , обозначаемый , равен 2 , поскольку 2 3 = 8 , в то время как другие кубические корни числа 8 равны и . Три кубических корня числа −27 i равны:
В некоторых контекстах, особенно когда число, кубический корень которого необходимо извлечь, является действительным числом, один из кубических корней (в данном случае действительный) называется главным кубическим корнем , обозначаемым знаком радикала. Кубический корень является обратной функцией кубической функции , если рассматривать только действительные числа, но не если рассматривать также комплексные числа: хотя всегда куб ненулевого числа имеет более одного комплексного кубического корня, и его главный кубический корень может не быть числом, которое было возведено в куб. Например, , но


Формальное определение
Кубические корни числа x — это числа y , которые удовлетворяют уравнению
Характеристики
Реальные цифры
Для любого действительного числа x существует одно действительное число y такое, что y 3 = x . Функция куба возрастает, поэтому не дает одинаковый результат для двух разных входных данных, и она охватывает все действительные числа. Другими словами, это биекция, или взаимно-однозначное соответствие. Тогда мы можем определить обратную функцию, которая также является взаимно-однозначной. Для действительных чисел мы можем определить уникальный кубический корень всех действительных чисел. Если использовать это определение, кубический корень отрицательного числа является отрицательным числом.
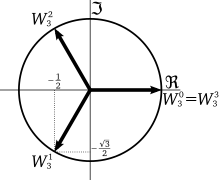
Если x и y могут быть комплексными , то существует три решения (если x не равен нулю), и поэтому x имеет три кубических корня. Действительное число имеет один действительный кубический корень и еще два кубических корня, которые образуют комплексно-сопряженную пару. Например, кубические корни 1 :
Последние два из этих корней приводят к связи между всеми корнями любого действительного или комплексного числа. Если число является одним кубическим корнем определенного действительного или комплексного числа, другие два кубических корня могут быть найдены путем умножения этого кубического корня на один или другой из двух комплексных кубических корней 1.
Комплексные числа


Для комплексных чисел главный кубический корень обычно определяется как кубический корень, имеющий наибольшую действительную часть , или, что то же самое, кубический корень, аргумент которого имеет наименьшее абсолютное значение . Он связан с главным значением натурального логарифма формулой
Если мы запишем x как
где r — неотрицательное действительное число, а θ лежит в диапазоне
- ,
тогда главный комплексный кубический корень равен
Это означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, чтобы определить кубический корень. При таком определении главный кубический корень отрицательного числа является комплексным числом, и, например, 3 √ −8 будет не −2, а 1 + i √ 3 .
Эту трудность можно решить, рассматривая кубический корень как многозначную функцию : если мы запишем исходное комплексное число x в трех эквивалентных формах, а именно:

Главные комплексные кубические корни этих трех форм тогда соответственно равны
Если только x = 0 , эти три комплексных числа различны, даже если три представления x были эквивалентны. Например, 3 √ −8 может быть вычислено как −2, 1 + i √ 3 или 1 − i √ 3 .
Это связано с концепцией монодромии : если следовать непрерывности функции кубического корня по замкнутому пути вокруг нуля, то после поворота значение кубического корня умножается (или делится) на
Невозможность построения с помощью циркуля и линейки
Кубические корни возникают в задаче нахождения угла, мера которого составляет одну треть от заданного угла ( трисекция угла ), и в задаче нахождения ребра куба, объем которого вдвое больше объема куба с заданным ребром ( удвоение куба ). В 1837 году Пьер Ванцель доказал, что ни одно из этих построений не может быть выполнено с помощью циркуля и линейки .
Численные методы
Метод Ньютона — это итеративный метод , который можно использовать для вычисления кубического корня. Для действительных чисел с плавающей точкой этот метод сводится к следующему итеративному алгоритму для получения последовательно лучших приближений кубического корня a :
Метод просто усредняет три фактора, выбранных таким образом, что
на каждой итерации.
Метод Галлея улучшает этот алгоритм, предлагая алгоритм, который сходится быстрее с каждой итерацией, хотя и с большим объемом работы на итерацию:
Это сходится кубически , поэтому две итерации выполняют столько же работы, сколько три итерации метода Ньютона. Каждая итерация метода Ньютона стоит два умножения, одно сложение и одно деление, предполагая, что 1/3 a вычисляется заранее, поэтому три итерации плюс предварительное вычисление требуют семи умножений, трех сложений и трех делений.
Каждая итерация метода Галлея требует трех умножений, трех сложений и одного деления, [1] поэтому две итерации обходятся в шесть умножений, шесть сложений и два деления. Таким образом, метод Галлея имеет потенциал быть быстрее, если одно деление дороже трех сложений.
В любом из методов плохое начальное приближение x 0 может дать очень плохую производительность алгоритма, и получение хорошего начального приближения является своего рода черной магией. Некоторые реализации манипулируют битами экспоненты числа с плавающей точкой; т. е. они достигают начального приближения путем деления экспоненты на 3. [1]
Также полезна эта обобщенная цепная дробь , основанная на методе корня n-й степени :
Если x является хорошим первым приближением к кубическому корню из a и y = a − x 3 , то:
Второе уравнение объединяет каждую пару дробей из первого в одну дробь, тем самым удваивая скорость сходимости.
Появление в решениях уравнений третьей и четвертой степени
Кубические уравнения , которые являются полиномиальными уравнениями третьей степени (то есть наибольшая степень неизвестного равна 3), всегда могут быть решены для их трех решений в терминах кубических корней и квадратных корней (хотя более простые выражения только в терминах квадратных корней существуют для всех трех решений, если хотя бы одно из них является рациональным числом ). Если два из решений являются комплексными числами, то все три выражения решения включают действительный кубический корень действительного числа, в то время как если все три решения являются действительными числами, то они могут быть выражены в терминах комплексного кубического корня комплексного числа .
Уравнения четвертой степени также можно решить с помощью кубических и квадратных корней.
История
Вычисление кубических корней можно проследить до вавилонских математиков еще с 1800 г. до н. э. [2] В четвертом веке до н. э. Платон сформулировал задачу удвоения куба , которая требовала построения с помощью циркуля и линейки ребра куба с объемом, вдвое большим заданного куба; это требовало построения, которое теперь известно как невозможное, длины 3 √ 2 .
Метод извлечения кубических корней описан в «Девяти главах математического искусства» , китайском математическом тексте, составленном около второго века до нашей эры и прокомментированном Лю Хуэем в третьем веке нашей эры. [3] Греческий математик Герон Александрийский разработал метод вычисления кубических корней в первом веке нашей эры. Его формула снова упоминается Евтокием в комментарии к «Архимеду» . [4] В 499 году нашей эры Арьябхата , математик - астроном из классической эпохи индийской математики и индийской астрономии , дал метод нахождения кубического корня из чисел, имеющих много цифр, в «Арьябхатии» (раздел 2.5). [5]
Смотрите также
- Методы вычисления квадратных корней
- Список полиномиальных тем
- Корень степени N
- Квадратный корень
- Вложенный радикал
- Корень единства
Ссылки
- ^ ab "В поисках быстрого кубического корня". metamerist.com . 2008. Архивировано из оригинала 27 декабря 2013 г.
- ^ Saggs, HWF (1989). Цивилизация до Греции и Рима . Yale University Press. стр. 227. ISBN 978-0-300-05031-8.
- ^ Кроссли, Джон; В.-К. Лун, Энтони (1999). Девять глав о математическом искусстве: Компаньон и комментарий. Oxford University Press. стр. 213. ISBN 978-0-19-853936-0.
- ^ Smyly, J. Gilbart (1920). «Формула Герона для кубического корня». Hermathena . 19 (42). Тринити-колледж Дублин: 64–67. JSTOR 23037103.
- ^ Арьябхатия. Архивировано 15 августа 2011 года в archive.today. Маратхи : आर्यभटीय , Мохан Апте, Пуна, Индия, Rajhans Publications, 2009, стр. 62, ISBN 978-81-7434-480-9
Внешние ссылки
- Калькулятор кубического корня приводит любое число к простейшей радикальной форме
- Вычисление кубического корня, Кен Турковски, Технический отчет Apple № KT-32, 1998. Включает исходный код на языке C.
- Вайсштейн, Эрик В. "Кубический корень". MathWorld .
![{\displaystyle {\sqrt[{3}]{8}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/513fcbe75ae8a28fbf5b6a762df26f92fa74ff1a)



![{\displaystyle {\sqrt[{3}]{~^{~}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cad47b3b9eed327000ea93a2a0f0eec715bf0e27)
![{\displaystyle \left({\sqrt[{3}]{x}}\right)^{3}=x,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/21ec18fc45aa08e653a9c21432184bc7ff422b0b)

![{\displaystyle {\sqrt[{3}]{8}}=2.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4a48fd5e8236aac9e692a05eace9e32816df87e)





![{\displaystyle {\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp \left({\frac {i\theta}{3}}\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b98750564191c9097532704595eaa97dd435633)
![{\displaystyle x={\begin{cases}r\exp(i\theta ),\\[3px]r\exp(i\theta +2i\pi ),\\[3px]r\exp(i\theta -2i\pi ).\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24bbbc0717e25337093a26c26f3e911ab2505219)
![{\displaystyle {\sqrt[{3}]{x}}={\begin{cases}{\sqrt[{3}]{r}}\exp \left({\frac {i\theta }{3}}\right),\\{\sqrt[{3}]{r}}\exp \left({\frac {i\theta }{3}}+{\frac {2i\pi }{3}}\right),\\{\sqrt[{3}]{r}}\exp \left({\frac {i\theta }{3}}-{\frac {2i\pi }{3}}\right).\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b70d19b99d4bd3640e90ef97a5295704f825b49a)




![{\displaystyle {\sqrt[{3}]{a}}={\sqrt[{3}]{x^{3}+y}}=x+{\cfrac {y}{3x^{2}+{\cfrac {2y}{2x+{\cfrac {4y}{9x^{2}+{\cfrac {5y}{2x+{\cfrac {7y}{15x^{2}+{\cfrac {8y}{2x+\ddots }}}}}}}}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53b1538138f23bc34e142a7a4fb13ca3c362922d)
