Ориентированный матроид

Ориентированный матроид — это математическая структура , которая абстрагирует свойства направленных графов , векторных расположений над упорядоченными полями и гиперплоскостных расположений над упорядоченными полями . ^[1] Для сравнения, обычный (т.е. неориентированный) матроид абстрагирует свойства зависимости , которые являются общими как для графов , которые не обязательно направлены , так и для расположений векторов над полями , которые не обязательно упорядочены . ^{[2] [3]}

Все ориентированные матроиды имеют базовый матроид . Таким образом, результаты для обычных матроидов могут быть применены к ориентированным матроидам. Однако обратное неверно ; некоторые матроиды не могут стать ориентированными матроидами, ориентируя базовую структуру (например, схемы или независимые множества). ^[4] Различие между матроидами и ориентированными матроидами обсуждается ниже.

Матроиды часто полезны в таких областях, как теория размерности и алгоритмы . Благодаря включению в ориентированный матроид дополнительных деталей об ориентированной природе структуры, его полезность распространяется далее на несколько областей, включая геометрию и оптимизацию .

Первое упоминание ориентированных матроидов было в статье Джорджа Дж. Минти 1966 года и ограничивалось регулярными матроидами . ^[5]

Впоследствии RT Rockefellar (1969) предложил задачу обобщения концепции Минти на вещественные векторные пространства. Его предложение помогло привести к разработке общей теории.

Чтобы абстрагировать концепцию ориентации на ребрах графа к множествам, необходимо иметь возможность назначать «направление» элементам множества. Это достигается следующим определением знаковых множеств .

• Знаковый набор , , объединяет набор объектов, , с упорядоченным двукратным разбиением этого набора на два непересекающихся подмножества: и .${\displaystyle X}$${\displaystyle {\underline {X}}}$ ${\displaystyle (X^{+},X^{-})}$${\displaystyle X^{+}}$${\displaystyle X^{-}}$

Члены называются положительными элементами ; члены — отрицательными элементами .${\displaystyle X^{+}}$${\displaystyle X^{-}}$

• Набор называется поддержкой .​${\displaystyle {\underline {X}}=X^{+}\cup X^{-}}$${\displaystyle X}$
• Пустое знаковое множество , , определяется как пустое множество, объединенное с (упорядоченным) его двуразделом на два пустых множества: и .${\displaystyle \emptyset}$${\displaystyle {\underline {\emptyset }}}$${\displaystyle \emptyset ^{+}}$${\displaystyle \emptyset ^{-}}$
• Знаковое множество противоположно , записано , если и${\displaystyle Y}$${\displaystyle X}$${\displaystyle Y=-X}$${\displaystyle Y^{+}=X^{-}}$${\displaystyle Y^{-}=X^{+}.}$

При наличии элемента поддержки мы запишем для положительного элемента и для отрицательного элемента. Таким образом, знаковый набор просто добавляет отрицательные знаки к выделенным элементам. Это будет иметь смысл как «направление» только тогда, когда мы рассмотрим ориентации более крупных структур. Тогда знак каждого элемента будет кодировать его направление относительно этой ориентации.${\displaystyle x}$${\displaystyle x}$${\displaystyle -x}$

Как и в случае с обычными матроидами, существует несколько эквивалентных систем аксиом . (Такие структуры, обладающие несколькими эквивалентными аксиоматизациями, называются криптоморфными .)

Пусть будет любым набором. Мы называем базовым набором . Пусть будет набором знаковых наборов , каждый из которых поддерживается подмножеством . Если следующие аксиомы верны для , то эквивалентно является набором знаковых схем для ориентированного матроида на .${\displaystyle E}$${\displaystyle E}$${\displaystyle {\mathcal {C}}}$${\displaystyle E}$${\displaystyle {\mathcal {C}}}$${\displaystyle {\mathcal {C}}}$${\displaystyle E}$

• (С0)${\displaystyle \emptyset \notin {\mathcal {C}}}$
• (С1) (симметричный)${\displaystyle {\text{ Для всех }}X\in {\mathcal {C}},~-\!X\in {\mathcal {C}}.}$
• (C2) (несравненный)${\displaystyle {\text{ Для всех }}X,Y\in {\mathcal {C}},~~{\text{ если }}{\underline {X}}\subseteq {\underline {Y}}{\text{ тогда }}(X=Y{\text{ или }}X=-Y).}$
• (C3) (слабое исключение)${\displaystyle {\text{ Для всех }}X,Y\in {\mathcal {C}},X\neq -Y{\text{ с }}e\in X^{+}\cap Y^{-}{\text{ существует }}Z\in {\mathcal {C}}{\text{ такой, что }}}$
  • ${\displaystyle Z^{+}\subseteq (X^{+}\cup Y^{+})\setminus \{e\}{\text{ и }}}$
  • ${\displaystyle Z^{-}\subseteq (X^{-}\cup Y^{-})\setminus \{e\}.}$

Композиция знаковых множеств и есть знаковое множество, определяемое , , и . Векторы ориентированного матроида являются композициями цепей. Векторы ориентированного матроида удовлетворяют следующим аксиомам:${\displaystyle X}$${\displaystyle Y}$${\displaystyle X\circ Y}$${\displaystyle {\underline {X\circ Y}}={\underline {X}}\cup {\underline {Y}}}$${\displaystyle (X\circ Y)^{+}=X^{+}\cup \left(Y^{+}\setminus X^{-}\right)}$${\displaystyle (X\circ Y)^{-}=X^{-}\cup \left(Y^{-}\setminus X^{+}\right)}$${\displaystyle {\mathcal {V}}}$

• ${\displaystyle \emptyset \in {\mathcal {V}}}$
• ${\displaystyle {\mathcal {V}}=- {\mathcal {V}}}$
• для всех ,${\displaystyle X,Y\in {\mathcal {V}}}$${\displaystyle X\circ Y\in {\mathcal {V}}}$
• для всех , и , существует , такой что${\displaystyle X,Y\in {\mathcal {V}}}$${\displaystyle e\in X^{+}\cap Y^{-}}$${\displaystyle f\in ({\underline {X}}\setminus {\underline {Y}})\cup ({\underline {Y}}\setminus {\underline {X}})\cup (X^{+}\cap Y^{+})\cup (X^{-}\cap Y^{-})}$${\displaystyle Z\in {\mathcal {V}}}$
  • ${\displaystyle Z^{+}\subset X^{+}\cup Y^{+}\setminus e}$,
  • ${\displaystyle Z^{-}\subset X^{-}\cup Y^{-}\setminus e}$, и
  • ${\displaystyle f\in {\underline {Z}}}$.

Ковекторы ориентированного матроида являются векторами его двойственного ориентированного матроида .

Пусть будет как выше. Для каждого неотрицательного целого числа хиротоп ранга — это функция , которая удовлетворяет следующим аксиомам:${\displaystyle E}$${\displaystyle r}$${\displaystyle r}$${\displaystyle \chi \colon E^{r}\to \{-1,0,1\}}$

• (B0) (нетривиально) : не является тождественно нулем${\displaystyle \чи}$
• (B1) (чередование) : Для любой перестановки и , , где — знак перестановки.${\displaystyle \сигма}$${\displaystyle x_{1},\dots ,x_{r}\in E}$${\displaystyle \chi \left(x_{\sigma (1)},\dots ,x_{\sigma (r)}\right)=\operatorname {sgn} (\sigma )\chi \left(x_{1},\dots ,x_{r}\right)}$${\displaystyle \operatorname {sgn} (\sigma )}$
• (B2) (обмен) : Для любого такого, что для каждого , тогда мы также имеем .${\displaystyle x_{1},\dots ,x_{r},y_{1},\dots ,y_{r}\in E}$${\displaystyle \chi (y_{i},x_{2},\dots ,x_{r})\chi (y_{1},\dots ,y_{i-1},x_{1},y_{i+1},\dots ,y_{r})\geq 0}$${\displaystyle я}$${\displaystyle \chi \left(x_{1},\dots ,x_{r}\right)\chi \left(y_{1},\dots ,y_{r}\right)\geq 0}$

Термин «хиротоп» происходит от математического понятия хиральности , которое представляет собой концепцию, взятую из химии , где оно используется для различения молекул, имеющих одинаковую структуру, за исключением отражения.

Каждый хиротоп ранга порождает набор баз матроида на , состоящий из тех подмножеств -элементов, которые присваивают ненулевое значение. ^[6] Хиротоп затем может подписать контуры этого матроида. Если является контуром описанного матроида, то где является базисом. Тогда может быть подписано положительными элементами${\displaystyle r}$${\displaystyle E}$${\displaystyle r}$${\displaystyle \чи}$${\displaystyle C}$${\displaystyle C\subset \{x_{1},\dots ,x_{r},x_{r+1}\}}$${\displaystyle \{x_{1},\dots ,x_{r}\}}$${\displaystyle C}$

${\displaystyle C^{+}=\{x_{i}:(-1)^{i}\chi (x_{1},\dots ,x_{i-1},x_{i+1},\dots ,x_{r+1})=1\}}$

и отрицательные элементы — дополнение. Таким образом, хиротоп порождает ориентированные базы ориентированного матроида. В этом смысле (B0) — непустая аксиома для баз, а (B2) — свойство обмена баз.

Ориентированные матроиды часто вводятся (например, Бахемом и Керном) как абстракция для ориентированных графов или систем линейных неравенств. Ниже приведены явные конструкции.

Для заданного орграфа мы определяем знаковый контур из стандартного контура графа следующим способом. Носителем знакового контура является стандартный набор ребер в минимальном цикле. Мы идем по циклу по часовой стрелке или против часовой стрелки, назначая те ребра, ориентация которых согласуется с направлением, положительным элементам , а те ребра, ориентация которых не согласуется с направлением, отрицательным элементам . Если — множество всех таких , то — множество знаковых контуров ориентированного матроида на множестве ребер ориентированного графа.${\displaystyle \textstyle {\underline {X}}}$${\displaystyle \textstyle X^{+}}$${\displaystyle \textstyle X^{-}}$${\displaystyle \textstyle {\mathcal {C}}}$${\displaystyle \textstyle X}$${\displaystyle \textstyle {\mathcal {C}}}$

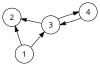
Если мы рассмотрим ориентированный граф справа, то увидим, что существует только два контура, а именно и . Тогда существует только четыре возможных знаковых контура, соответствующих ориентациям по часовой стрелке и против часовой стрелки, а именно , , , и . Эти четыре набора образуют набор знаковых контуров ориентированного матроида на множестве .${\displaystyle \textstyle \{(1,2),(1,3),(3,2)\}}$${\displaystyle \textstyle \{(3,4),(4,3)\}}$${\displaystyle \textstyle \{(1,2),-(1,3),-(3,2)\}}$${\displaystyle \textstyle \{-(1,2),(1,3),(3,2)\}}$${\displaystyle \textstyle \{(3,4),(4,3)\}}$${\displaystyle \textstyle \{-(3,4),-(4,3)\}}$${\displaystyle \textstyle \{(1,2),(1,3),(3,2),(3,4),(4,3)\}}$

Если — любое конечное подмножество , то множество минимальных линейно зависимых множеств образует множество схем матроида на . Чтобы распространить эту конструкцию на ориентированные матроиды, для каждой схемы существует минимальная линейная зависимость${\displaystyle \textstyle E}$${\displaystyle \textstyle \mathbb {R} ^{n}}$${\displaystyle \textstyle E}$${\displaystyle \textstyle \{v_{1},\dots ,v_{m}\}}$

${\displaystyle \sum _{i=1}^{m}\lambda _{i}v_{i}=0}$

с . Тогда знаковая схема имеет положительные элементы и отрицательные элементы . Множество всех таких элементов образует множество знаковых схем ориентированного матроида на . Ориентированные матроиды, которые могут быть реализованы таким образом, называются представимыми .${\displaystyle \textstyle \lambda _{i}\in \mathbb {R} }$${\displaystyle \textstyle X=\{X^{+},X^{-}\}}$${\displaystyle \textstyle X^{+}=\{v_{i}:\lambda _{i}>0\}}$${\displaystyle \textstyle X^{-}=\{v_{i}:\lambda _{i}<0\}}$${\displaystyle \textstyle X}$${\displaystyle \textstyle E}$

Учитывая тот же набор векторов , мы можем определить тот же ориентированный матроид с хиротопом . Для любого пусть${\displaystyle E}$${\displaystyle \chi :E^{r}\rightarrow \{-1,0,1\}}$${\displaystyle x_{1},\dots ,x_{r}\in E}$

${\displaystyle \chi (x_{1},\dots ,x_{r})=\operatorname {sgn} (\det(x_{1},\dots ,x_{r}))}$

где правая часть уравнения — знак определителя . Тогда — хиротоп того же ориентированного матроида на множестве .${\displaystyle \chi }$${\displaystyle E}$

Реальное расположение гиперплоскостей — это конечный набор гиперплоскостей в , каждая из которых содержит начало координат. Выбрав одну сторону каждой гиперплоскости в качестве положительной стороны, мы получаем расположение полупространств. Расположение полупространств разбивает окружающее пространство на конечный набор ячеек, каждая из которых определяется тем, на какой стороне каждой гиперплоскости она находится. То есть, назначаем каждую точку знаковому набору с , если находится на положительной стороне , и если находится на отрицательной стороне . Этот набор знаковых наборов определяет набор ковекторов ориентированного матроида, которые являются векторами двойственного ориентированного матроида. ^[7]${\displaystyle {\mathcal {A}}=\{H_{1},\ldots ,H_{n}\}}$${\displaystyle \mathbb {R} ^{d}}$${\displaystyle x\in \mathbb {R} ^{d}}$${\displaystyle X=(X^{+},X^{-})}$${\displaystyle i\in X^{+}}$${\displaystyle x}$${\displaystyle H_{i}}$${\displaystyle i\in X^{-}}$${\displaystyle x}$${\displaystyle H_{i}}$

Гюнтер М. Циглер вводит ориентированные матроиды через выпуклые многогранники.

Стандартный матроид называется ориентируемым, если его контуры являются опорами знаковых контуров некоторого ориентированного матроида. Известно, что все вещественные представимые матроиды ориентируемы. Известно также, что класс ориентируемых матроидов замкнут относительно взятия миноров , однако известно, что список запрещенных миноров для ориентируемых матроидов бесконечен. ^[8] В этом смысле ориентированные матроиды являются гораздо более строгой формализацией, чем регулярные матроиды.

Так же, как матроид имеет уникальный дуал , ориентированный матроид имеет уникальный дуал, часто называемый его «ортогональным дуалом». Это означает, что базовые матроиды являются дуалами, а косхемы подписаны так, что они «ортогональны» каждой схеме. Два знаковых множества называются ортогональными , если пересечение их носителей пусто или если ограничение их положительных элементов на пересечение и отрицательных элементов на пересечение образуют два неидентичных и непротивоположных знаковых множества. Существование и уникальность двойственного ориентированного матроида зависит от того факта, что каждая знаковая схема ортогональна каждой знаковой косхеме. ^[9]

Чтобы увидеть, почему ортогональность необходима для уникальности, достаточно взглянуть на пример орграфа выше. Мы знаем, что для планарных графов дуальный матроид контура является матроидом контура планарного дуального графа . Таким образом, существует столько же различных дуальных пар ориентированных матроидов, основанных на матроиде графа, сколько существует способов сориентировать граф и соответствующим образом его дуальный.

Чтобы увидеть явное построение этого уникального ортогонального дуально ориентированного матроида, рассмотрим хиротоп ориентированного матроида . Если мы рассматриваем список элементов как циклическую перестановку, то мы определяем быть знаком соответствующей перестановки. Если определяется как${\displaystyle \chi :E^{r}\rightarrow \{-1,0,1\}}$${\displaystyle x_{1},\dots ,x_{k}\in E}$${\displaystyle \operatorname {sgn} (x_{1},\dots ,x_{k})}$${\displaystyle \chi ^{*}:E^{|E|-r}\rightarrow \{-1,0,1\}}$

${\displaystyle \chi ^{*}(x_{1},\dots ,x_{r})\mapsto \chi (x_{r+1},\dots ,x_{|E|})\operatorname {sgn} (x_{1},\dots ,x_{r},x_{r+1},\dots ,x_{|E|}),}$

тогда это хиротоп уникального ортогонального дуально ориентированного матроида. ^[10]${\displaystyle \chi ^{*}}$

Не все ориентированные матроиды представимы, то есть не все имеют реализации в виде точечных конфигураций или, что эквивалентно, гиперплоскостных расположений. Однако в некотором смысле все ориентированные матроиды близки к тому, чтобы иметь реализации в виде гиперплоскостных расположений. В частности, теорема о топологическом представлении Фолкмана–Лоуренса утверждает, что любой ориентированный матроид имеет реализацию в виде расположения псевдосфер . -мерная псевдосфера является вложением , при котором существует гомеоморфизм , такой что вкладывается в качестве экватора . В этом смысле псевдосфера — это просто ручная сфера (в отличие от диких сфер ). Расположение псевдосфер в представляет собой набор псевдосфер, пересекающихся вдоль псевдосфер. Наконец, теорема о топологическом представлении Фолкмана–Лоуренса утверждает, что каждый ориентированный матроид ранга может быть получен из расположения псевдосфер в . ^[11] Он назван в честь Джона Фолкмана и Джима Лоуренса, которые опубликовали его в 1978 году.${\displaystyle d}$${\displaystyle e:S^{d}\hookrightarrow S^{d+1}}$${\displaystyle h:S^{d+1}\rightarrow S^{d+1}}$${\displaystyle h\circ e}$${\displaystyle S^{d}}$${\displaystyle S^{d+1}}$${\displaystyle S^{d}}$${\displaystyle d+1}$${\displaystyle S^{d}}$

Теория ориентированных матроидов оказала влияние на развитие комбинаторной геометрии , особенно на теорию выпуклых многогранников , зонотопов и конфигураций векторов (эквивалентно, расположений гиперплоскостей ). ^[12] Многие результаты — теорема Каратеодори , теорема Хелли , теорема Радона , теорема Хана–Банаха , теорема Крейна–Мильмана , лемма Фаркаша — могут быть сформулированы с использованием соответствующих ориентированных матроидов. ^[13]

Разработка системы аксиом для ориентированных матроидов была инициирована Р. Тирреллом Рокафелларом для описания знаковых моделей матриц, возникающих в результате поворотных операций симплексного алгоритма Данцига; Рокафеллар был вдохновлен исследованиями Альберта В. Такера таких знаковых моделей в «таблицах Такера». ^[14]

Теория ориентированных матроидов привела к прорывам в комбинаторной оптимизации . В линейном программировании это был язык, на котором Роберт Г. Блэнд сформулировал свое правило поворота , с помощью которого симплексный алгоритм избегает циклов. Аналогично, его использовали Терлаки и Чжан, чтобы доказать, что их перекрестные алгоритмы имеют конечное завершение для задач линейного программирования . Аналогичные результаты были получены в выпуклом квадратичном программировании Тоддом и Терлаки. ^[15] Он был применен к линейно-дробному программированию , ^{[16] задачам} квадратичного программирования и задачам линейной комплементарности . ^{[17] [18] [19]}

За пределами комбинаторной оптимизации ориентированная теория матроидов также появляется в выпуклой минимизации в теории Рокафеллара «монотропного программирования» и связанных с ней понятиях «укрепленного спуска». ^[20] Аналогичным образом теория матроидов повлияла на разработку комбинаторных алгоритмов, в частности жадного алгоритма . ^[21] В более общем смысле жадоид полезен для изучения конечного завершения алгоритмов.

• Бахем, Ахим; Керн, Уолтер (1992). Двойственность линейного программирования: введение в ориентированные матроиды . Universitext. Springer-Verlag. doi :10.1007/978-3-642-58152-6. ISBN 978-3-540-55417-2. МР  1230380.
• Бьёрнер, Андерс ; Лас Верньяс, Мишель ; Штурмфельс, Бернд ; Уайт, Нил; Циглер, Гюнтер (1999). Ориентированные матроиды . Энциклопедия математики и ее приложений. Т. 46 (2-е изд.). Cambridge University Press . ISBN 978-0-521-77750-6. Збл  0944.52006.
• Боковски, Юрген (2006). Вычислительно-ориентированные матроиды. Классы эквивалентности матриц в естественном каркасе . Cambridge University Press . ISBN 978-0-521-84930-2. Збл  1120.52011.
• Лоулер, Юджин (2001). Комбинаторная оптимизация: сети и матроиды . Дувр. ISBN 978-0-486-41453-9. Збл  1058.90057.
• Эвар Д. Неринг и Альберт В. Такер , 1993, Линейные программы и смежные проблемы , Academic Press. (элементарный)
• Рокафеллар, Р. Тиррелл (1984). Сетевые потоки и монотропная оптимизация . Wiley-Interscience.переиздано Athena Scientific Дмитрия Берцекаса , 1998.
• Циглер, Гюнтер М. (1994). Лекции по многогранникам . Нью-Йорк: Springer-Verlag.
• Рихтер-Геберт, Юрген; Циглер, Гюнтер М. (1997). «Ориентированные матроиды». В Гудмане, Джейкоб Э .; О'Рурк, Джозеф (ред.). Справочник по дискретной и вычислительной геометрии . Бока-Ратон: CRC Press. стр. 111–132. ISBN 9780849385247.

• А. Бахем, А. Ванка, Теоремы разделения для ориентированных матроидов, Дискретная математика. 70 (1988) 303–310.
• Бланд, Роберт Г. (1977). «Новые правила конечного поворота для симплекс-метода». Математика исследования операций . 2 (2): 103– 107. doi :10.1287/moor.2.2.103.
• Фолкман, Джон ; Лоуренс, Джим (октябрь 1978 г.). «Ориентированные матроиды». Журнал комбинаторной теории . Серия B. 25 (2): 199– 236. doi : 10.1016/0095-8956(78)90039-4 .
• Фукуда, Комей ; Терлаки, Тамас (1997). Томас М. Либлинг; Доминик де Верра (ред.). «Методы крест-накрест: свежий взгляд на алгоритмы поворота» (PDF) . Математическое программирование, серия B. 79 ( 1–3 ) . Амстердам: North-Holland Publishing Co.: 369–395 . doi :10.1007/BF02614325. MR  1464775. S2CID  2794181.
• Фукуда, Комей ; Намики, Макото (март 1994 г.). «Об экстремальном поведении метода наименьшего индекса Мурти». Математическое программирование . 64 (1): 365–370 . doi :10.1007/BF01582581. MR  1286455. S2CID  21476636.
• Иллес, Тибор; Ширмаи, Акос; Терлаки, Тамаш (1999). «Метод конечного креста для гиперболического программирования». Европейский журнал операционных исследований . 114 (1): 198–214 . CiteSeerX  10.1.1.36.7090 . дои : 10.1016/S0377-2217(98)00049-6. ISSN  0377-2217.
• Р. Тиррелл Рокафеллар (1969). Элементарные векторы подпространства , в книге «Комбинаторная математика и ее приложения» , RC Bose и TA Dowling (ред.), Univ. of North Carolina Press, стр. 104–127.${\displaystyle R^{n}}$
• Roos, C. (1990). "Экспоненциальный пример правила поворота Терлаки для метода симплекса крест-накрест". Математическое программирование . Серия A. 46 (1): 79– 84. doi :10.1007/BF01585729. MR  1045573. S2CID  33463483.
• Терлаки, Т. (1985). «Сходящийся метод крест-накрест». Оптимизация: Журнал математического программирования и исследования операций . 16 (5): 683– 690. doi :10.1080/02331938508843067. ISSN  0233-1934. MR  0798939.
• Терлаки, Тамаш (1987). "Конечный метод перекрестных вычислений для ориентированных матроидов". Журнал комбинаторной теории . Серия B. 42 (3): 319– 327. doi : 10.1016/0095-8956(87)90049-9 . ISSN  0095-8956. MR  0888684.
• Терлаки, Тамаш; Чжан, Шу Чжун (1993). «Правила осевого программирования для линейного программирования: обзор последних теоретических разработок». Annals of Operations Research . 46– 47 (1): 203– 233. CiteSeerX  10.1.1.36.7658 . doi :10.1007/BF02096264. ISSN  0254-5330. MR  1260019. S2CID  6058077.
• Тодд, Майкл Дж. (1985). «Линейное и квадратичное программирование в ориентированных матроидах». Журнал комбинаторной теории . Серия B. 39 (2): 105– 133. doi : 10.1016/0095-8956(85)90042-5 .
• Ван, Чжэ Минь (1987). «Конечный свободный от конформного исключения алгоритм над ориентированным матроидным программированием». Китайские анналы математики (Shuxue Niankan B Ji) . Серия B. 8 (1): 120– 125. ISSN  0252-9599. MR  0886756.

• Циглер, Гюнтер (1998). «Ориентированные матроиды сегодня». Электронный журнал комбинаторики : DS4: 10 сентября–1998. doi :10.37236/25.
• Malkevitch, Joseph. "Oriented Matroids: The Power of Unification". Feature Column . American Mathematical Society . Получено 14.09.2009 .

• Комей Фукуда (ETH Zentrum, Цюрих) с публикациями, включая «Ориентированное матроидное программирование» (кандидатская диссертация 1982 г.)
• Тамаш Терлаки (Университет Лихай) с публикациями