Буферный раствор

Кислоты и основания
Номер акцептора Кислота Кислотно-щелочная реакция Кислотно-щелочной гомеостаз Сила кислоты Функция кислотности Амфотерность База Буферные растворы Константа диссоциации Номер донора Равновесная химия Извлечение Функция кислотности Гаммета рН Сродство к протону Самоионизация воды Титрование Катализ кислот Льюиса Разочарованная пара Льюисов Хиральная кислота Льюиса модель ECW
Типы кислот
Бренстед–Лоури Льюис Минерал Органический Окись Сильный Суперкислоты Слабый Твердый
Базовые типы
Бренстед–Лоури Льюис Органический Окись Сильный Супербазы Ненуклеофильный Слабый
в т е

Буферный раствор — это раствор, в котором pH существенно не меняется при разбавлении или при добавлении кислоты или основания при постоянной температуре. ^[1] Его pH изменяется очень мало при добавлении к нему небольшого количества сильной кислоты или основания . Буферные растворы используются как средство поддержания pH на почти постоянном уровне в самых разных химических применениях. В природе существует множество живых систем , которые используют буферизацию для регулирования pH. Например, система буферизации бикарбоната используется для регулирования pH крови , а бикарбонат также действует как буфер в океане .

Буферные растворы устойчивы к изменению pH из-за химического равновесия между слабой кислотой HA и ее сопряженным основанием A ⁻ :

Когда к равновесной смеси слабой кислоты и ее сопряженного основания добавляется сильная кислота, добавляются ионы водорода (H ⁺ ), и равновесие смещается влево в соответствии с принципом Ле Шателье . Из-за этого концентрация ионов водорода увеличивается на величину, меньшую ожидаемой для количества добавленной сильной кислоты. Аналогично, если к смеси добавляется сильная щелочь, концентрация ионов водорода уменьшается на величину, меньшую ожидаемой для количества добавленной щелочи. На рисунке 1 эффект проиллюстрирован с помощью имитированного титрования слабой кислоты с p K _a  = 4,7. Относительная концентрация недиссоциированной кислоты показана синим цветом, а ее сопряженного основания — красным. pH изменяется относительно медленно в буферной области, pH = p K _a  ± 1, с центром при pH = 4,7, где [HA] = [A ⁻ ]. Концентрация ионов водорода уменьшается на величину, меньшую ожидаемой, поскольку большая часть добавленного гидроксид-иона расходуется в реакции

и только небольшая часть расходуется в реакции нейтрализации (реакции, которая приводит к повышению pH)

Как только кислота депротонируется более чем на 95% , pH быстро повышается, поскольку большая часть добавленной щелочи расходуется в реакции нейтрализации.

Буферная емкость — это количественная мера устойчивости к изменению pH раствора, содержащего буферный агент, по отношению к изменению концентрации кислоты или щелочи. Ее можно определить следующим образом: ^{[2] [3]} где — бесконечно малое количество добавленного основания, или где — бесконечно малое количество добавленной кислоты. pH определяется как −log ₁₀ [H ⁺ ], а d (pH) — бесконечно малое изменение pH. $${\displaystyle \beta ={\frac {dC_{b}}{d(\mathrm {pH} )}},}$$${\displaystyle dC_{b}}$$${\displaystyle \beta =-{\frac {dC_{a}}{d(\mathrm {pH} )}},}$$${\displaystyle dC_{a}}$

При любом определении буферная емкость для слабой кислоты HA с константой диссоциации K _a может быть выражена как ^{[4] [5] [3]} где [H ⁺ ] - концентрация ионов водорода, а - общая концентрация добавленной кислоты. K _w - константа равновесия для самоионизации воды , равная 1,0 × 10 ⁻¹⁴ . Обратите внимание, что в растворе H ⁺ существует в виде иона гидроксония H ₃ O ⁺ , и дальнейшее гидратирование иона гидроксония оказывает незначительное влияние на равновесие диссоциации, за исключением случаев очень высокой концентрации кислоты. $${\displaystyle \beta =2.303\left([{\ce {H+}}]+{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}+{\frac {K_{\text{w}}}{[{\ce {H+}}]}}\right),}$$${\displaystyle T_{\text{HA}}}$

Это уравнение показывает, что существуют три области повышенной буферной емкости (см. рисунок 2).

• В центральной области кривой (на графике обозначена зеленым цветом) доминирует второй член, и буферная емкость возрастает до локального максимума при pH =  pK _a . Высота этого пика зависит от значения pK _a . Буферная емкость незначительна, когда концентрация [HA] буферного агента очень мала и увеличивается с увеличением концентрации буферного агента. ^[3] Некоторые авторы показывают только эту область на графиках буферной емкости. ^[2]$${\displaystyle \beta \approx 2.303{\frac {T_{{\ce {HA}}}K_{a}[{\ce {H+}}]}{(K_{a}+[{\ce {H+}}])^{2}}}.}$$
  Емкость буфера падает до 33% от максимального значения при pH = p K _a ± 1, до 10% при pH = p K _a ± 1,5 и до 1% при pH = p K _a ± 2. По этой причине наиболее полезный диапазон составляет приблизительно p K _a  ± 1. При выборе буфера для использования при определенном pH он должен иметь значение ap _K a как можно ближе к этому pH. ^[2]
• В случае сильнокислых растворов, pH менее 2 (на графике они окрашены в красный цвет), первый член уравнения доминирует, а буферная емкость экспоненциально возрастает с уменьшением pH: Это происходит из-за того, что второй и третий члены становятся незначительными при очень низком pH. Этот член не зависит от наличия или отсутствия буферного агента.$${\displaystyle \beta \approx 10^{-\mathrm {pH} }.}$$
• В случае сильнощелочных растворов, pH более 12 (на графике они окрашены в синий цвет), третий член уравнения доминирует, а буферная емкость экспоненциально возрастает с ростом pH: Это происходит из-за того, что первый и второй члены становятся незначительными при очень высоком pH. Этот член также не зависит от наличия или отсутствия буферного агента.$${\displaystyle \beta \approx 10^{\mathrm {pH} -\mathrm {p} K_{\text{w}}}.}$$

pH раствора, содержащего буферный агент, может изменяться только в узком диапазоне, независимо от того, что еще может присутствовать в растворе. В биологических системах это является необходимым условием для правильного функционирования ферментов . Например, в крови человека смесь угольной кислоты (H
₂КО
₃) и бикарбонат (HCO⁻
₃) присутствует во фракции плазмы ; это составляет основной механизм поддержания pH крови между 7,35 и 7,45. За пределами этого узкого диапазона (7,40 ± 0,05 единицы pH) быстро развиваются метаболические состояния ацидоза и алкалоза , в конечном итоге приводящие к смерти, если правильная буферная емкость не восстанавливается быстро.

Если значение pH раствора слишком сильно повышается или понижается, эффективность фермента снижается в процессе, известном как денатурация , который обычно необратим. ^[6] Большинство биологических образцов, используемых в исследованиях, хранятся в буферном растворе, часто в фосфатно-солевом буфере (PBS) при pH 7,4.

В промышленности буферные агенты используются в процессах ферментации и для установления правильных условий для красителей, используемых при окраске тканей. Они также используются в химическом анализе ^[5] и калибровке pH-метров .

Буферный агент	п К а	Полезный диапазон pH
лимонная кислота	3.13, 4.76, 6.40	2.1–7.4
уксусная кислота	4.8	3,8–5,8
КН 2 ПО 4	7.2	6.2–8.2
ЧЕС	9.3	8.3–10.3
Борат	9.24	8.25–10.25

Для буферов в кислотных областях pH можно отрегулировать до желаемого значения, добавив сильную кислоту, например, соляную кислоту, к конкретному буферному агенту. Для щелочных буферов можно добавить сильное основание, например, гидроксид натрия . В качестве альтернативы буферную смесь можно приготовить из смеси кислоты и сопряженного с ней основания. Например, ацетатный буфер можно приготовить из смеси уксусной кислоты и ацетата натрия . Аналогично щелочной буфер можно приготовить из смеси основания и сопряженной с ним кислоты.

Объединяя вещества со значениями p K _a , отличающимися всего на два или менее, и регулируя pH, можно получить широкий диапазон буферов. Лимонная кислота является полезным компонентом буферной смеси, поскольку она имеет три значения p K _a , разделенные менее чем на два. Диапазон буфера может быть расширен путем добавления других буферных агентов. Следующие смеси ( буферные растворы МакИлвейна ) имеют диапазон буфера от 3 до 8. ^[7]

0,2 М Na2HPO4 ( мл )	0,1 М лимонная кислота (мл)	рН
20.55	79.45	3.0
38,55	61.45	4.0
51.50	48.50	5.0
63.15	36.85	6.0
82.35	17.65	7.0
97.25	2.75	8.0

Смесь, содержащая лимонную кислоту , монокалийфосфат , борную кислоту и диэтилбарбитуровую кислоту , может быть приготовлена ​​для покрытия диапазона pH от 2,6 до 12. ^[8]

Другими универсальными буферами являются буфер Кармоди ^[9] и буфер Бриттона–Робинсона , разработанный в 1931 году.

Для эффективного диапазона см. Буферная емкость выше. Также см. Буферы Гуда для исторических принципов проектирования и благоприятных свойств этих буферных веществ в биохимических приложениях.

Общее название (химическое название)	Структура	р Ка , 25 ° С	Темп. эффект, ⁠dpH/д Т⁠ (К −1 ) [10]	Мол. вес
TAPS , ([трис(гидроксиметил)метиламино]пропансульфоновая кислота)		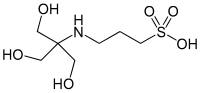8.43	−0,018	243.3
Бицин , (2-(бис(2-гидроксиэтил)амино)уксусная кислота)		8.35	−0,018	163.2
Трис , (трис(гидроксиметил)аминометан или 2-амино-2-(гидроксиметил)пропан-1,3-диол)		8.07 [а]	−0,028	121.14
Трицин , (N-[трис(гидроксиметил)метил]глицин)		8.05	−0,021	179.2
TAPSO , (3-[N-трис(гидроксиметил)метиламино]-2-гидроксипропансульфоновая кислота)		7.635		259.3
HEPES , (4-(2-гидроксиэтил)-1-пиперазинэтансульфоновая кислота)		7.48	−0,014	238.3
TES , (2-[[1,3-дигидрокси-2-(гидроксиметил)пропан-2-ил]амино]этансульфоновая кислота)		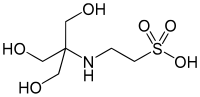7.40	−0,020	229.20
MOPS , (3-(N-морфолино)пропансульфоновая кислота)		7.20	−0,015	209.3
ТРУБЫ , (пиперазин-N,N′-бис(2-этансульфоновая кислота))		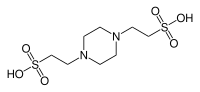6.76	−0,008	302.4
Какодилат ( диметилмышьяковая кислота)		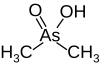6.27		138.0
MES , (2-(N-морфолино)этансульфоновая кислота)		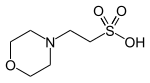6.15	−0,011	195.2

Сначала запишите выражение равновесия

Это показывает, что при диссоциации кислоты образуются равные количества ионов водорода и анионов. Равновесные концентрации этих трех компонентов можно рассчитать в таблице ICE (ICE означает «initial, change, balance»).

Таблица ICE для одноосновной кислоты

	[ХА]	[А − ]	[Н + ]
я	С 0	0	у
С	− х	х	х
Э	С 0 − х	х	х + у

Первая строка, обозначенная I , перечисляет начальные условия: концентрация кислоты равна C ₀ , изначально недиссоциированной, поэтому концентрации A ⁻ и H ⁺ будут равны нулю; y — начальная концентрация добавленной сильной кислоты, такой как соляная кислота. Если добавляется сильная щелочь, такая как гидроксид натрия, то y будет иметь отрицательный знак, потому что щелочь удаляет ионы водорода из раствора. Вторая строка, обозначенная C (изменение), определяет изменения, которые происходят при диссоциации кислоты. Концентрация кислоты уменьшается на величину − x , а концентрации A ⁻ и H ⁺ увеличиваются на величину + x . Это следует из выражения равновесия. Третья строка, обозначенная E (равновесие), складывает первые две строки и показывает концентрации при равновесии.

Чтобы найти x , воспользуйтесь формулой константы равновесия в терминах концентраций:$${\displaystyle K_{\text{a}}={\frac {[{\ce {H+}}][{\ce {A-}}]}{[{\ce {HA}}]}}.}$$

Замените концентрации значениями, найденными в последней строке таблицы ICE:$${\displaystyle K_{\text{a}}={\frac {x(x+y)}{C_{0}-x}}.}$$

Упростить до$${\displaystyle x^{2}+(K_{\text{a}}+y)x-K_{\text{a}}C_{0}=0.}$$

При определенных значениях C ₀ , K _a и y это уравнение можно решить относительно x . Предполагая, что pH = −log ₁₀ [H ⁺ ], pH можно рассчитать как pH = −log ₁₀ ( x  +  y ).

Полипротонные кислоты — это кислоты, которые могут терять более одного протона. Константа диссоциации первого протона может быть обозначена как K _a1 , а константы диссоциации последующих протонов как K _a2 и т. д. Лимонная кислота является примером полипротонной кислоты H ₃ A, поскольку она может терять три протона.

Константы ступенчатой ​​диссоциации

Равновесие	лимонная кислота
Н 3 А ⇌ Н 2 А − + Н +	п К а1 = 3,13
Н 2 А − ⇌ ХА 2− + Н +	п К а2 = 4,76
ХА 2− ⇌ А 3− + Н +	п К а3 = 6,40

Когда разница между последовательными значениями p K _a меньше примерно 3, существует перекрытие между диапазонами pH существования видов в равновесии. Чем меньше разница, тем больше перекрытие. В случае лимонной кислоты перекрытие обширно, и растворы лимонной кислоты буферизуются во всем диапазоне pH от 2,5 до 7,5.

Расчет pH с полипротонной кислотой требует проведения расчета видообразования . В случае лимонной кислоты это влечет за собой решение двух уравнений баланса масс:

$${\displaystyle {\begin{aligned}C_{{\ce {A}}}&=[{\ce {A^3-}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3},\\C_{{\ce {H}}}&=[{\ce {H+}}]+\beta _{1}[{\ce {A^3-}}][{\ce {H+}}]+2\beta _{2}[{\ce {A^3-}}][{\ce {H+}}]^{2}+3\beta _{3}[{\ce {A^3-}}][{\ce {H+}}]^{3}-K_{\text{w}}[{\ce {H+}}]^{-1}.\end{aligned}}}$$

C _A — аналитическая концентрация кислоты, C _H — аналитическая концентрация добавленных ионов водорода, β _q — кумулятивные константы ассоциации . K _w — константа самоионизации воды . Существуют два нелинейных одновременных уравнения с двумя неизвестными величинами [A ³⁻ ] и [H ⁺ ]. Для выполнения этого расчета доступно множество компьютерных программ. Диаграмма видообразования для лимонной кислоты была создана с помощью программы HySS. ^[11]

Примечание. Нумерация кумулятивных, общих констант обратна нумерации пошаговых, констант диссоциации.

Соотношение между значениями кумулятивной константы ассоциации (β) и значениями ступенчатой ​​константы диссоциации (K) для трехосновной кислоты.

Равновесие	Отношение
А 3− + Н + ⇌ АН 2+	Лог β 1 = pk a3
А 3− + 2Н + ⇌ АН 2 +	Лог β 2 =pk a2 + pk a3
А 3− + 3Н + ⇌ АН 3	Лог β 3 = pk a1 + pk a2 + pk a3

Кумулятивные константы ассоциации используются в универсальных компьютерных программах, таких как та, которая использовалась для получения диаграммы видообразования выше.

• Уравнение Хендерсона – Хассельбаха
• Буферы Гуда
• Эффект общего иона
• Буфер ионов металлов
• Минеральный окислительно-восстановительный буфер

«Биологические буферы». Устройства REACH.