Кубооктаэдр
Многогранник с 8 треугольными гранями и 6 квадратными гранями
Кубооктаэдр
ТипАрхимедовы тела
Лица14
Края24
Вершины12
Конфигурация вершины3.4.3.4
Группа симметрииОктаэдрическая симметрия Тетраэдрическая симметрия О час {\displaystyle \mathrm {O} _ {\mathrm {h} }}
Т г {\ displaystyle \ mathrm {T} _ {\ mathrm {d} }}
Двугранный угол ( градусы )приблизительно 125°
Двойной многогранникРомбический додекаэдр
Характеристикивыпуклый ,
векторное равновесие,
свойство Руперта
Вершинная фигура
Сеть

Кубооктаэдр — это многогранник с 8 треугольными гранями и 6 квадратными гранями. Кубооктаэдр имеет 12 одинаковых вершин , в каждой из которых сходятся 2 треугольника и 2 квадрата, и 24 одинаковых ребра , каждое из которых отделяет треугольник от квадрата. Таким образом, это квазиправильный многогранник , т. е. архимедово тело , которое не только вершинно-транзитивно , но и рёберно-транзитивно . [1] Он радиально равносторонний. Его двойственный многогранник — ромбический додекаэдр .

Строительство

Кубооктаэдр можно построить многими способами:

  • Его строительство можно начать, прикрепив два правильных треугольных купола основанием к основанию. Это похоже на одно из тел Джонсона, треугольный ортобикупол . Разница в том, что треугольный ортобикупол построен с одним из куполов, скрученным так, что подобные многоугольные грани являются смежными, тогда как кубооктаэдр - нет. В результате кубооктаэдр можно также назвать треугольным гиробикуполом . [2]
  • Его построение можно начать с куба или правильного октаэдра , отметив середины их ребер и отрезав все вершины в этих точках. Этот процесс известен как ректификация , в результате чего кубооктаэдр называют выпрямленным кубом и выпрямленным октаэдром . [3]
  • Альтернативное построение — это отрезание всех вершин, известное как усечение . можно начать с правильного тетраэдра , отрезая вершины и скашивая ребра. Этот процесс известен как кантеллирование , в результате чего кубооктаэдр называется кантеллированным тетраэдром . [4]

Из всех этих построений кубооктаэдр имеет 14 граней: 8 равносторонних треугольников и 6 квадратов. Он также имеет 24 ребра и 12 вершин. [5]

Декартовы координаты вершин кубооктаэдра с длиной ребра, центрированной в начале координат, следующие: [6] 2 {\displaystyle {\sqrt {2}}} ( ± 1 , ± 1 , 0 ) , ( ± 1 , 0 , ± 1 ) , ( 0 , ± 1 , ± 1 ) . {\displaystyle (\pm 1,\pm 1,0),\qquad (\pm 1,0,\pm 1),\qquad (0,\pm 1,\pm 1).}

Характеристики

Измерение и другие метрические свойства

Площадь поверхности кубооктаэдра можно определить, суммируя все площади его многоугольных граней. Объем кубооктаэдра можно определить, разрезав его на два правильных треугольных купола, суммируя их объемы. Учитывая, что длина ребра , его площадь поверхности и объем равны: [5] А {\displaystyle А} В {\displaystyle V} а {\displaystyle а} А = ( 6 + 2 3 ) а 2 ≈ 9.464 а 2 В = 5 2 3 а 3 ≈ 2.357 а 3 . {\displaystyle {\begin{aligned}A&=\left(6+2{\sqrt {3}}\right)a^{2}&&\approx 9.464a^{2}\\V&={\frac {5{\sqrt {2}}}{3}}a^{3}&&\approx 2.357a^{3}.\end{aligned}}}

Двугранный угол кубооктаэдра можно вычислить с помощью угла треугольных куполов. Двугранный угол треугольного купола между квадратом и треугольником составляет приблизительно 125°, между квадратом и шестиугольником составляет 54,7°, а между треугольником и шестиугольником составляет 70,5°. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником на ребре, где прикреплены основания двух треугольных куполов, составляет 54,7° + 70,5°, приблизительно 125°. Следовательно, двугранный угол кубооктаэдра между квадратом и треугольником составляет приблизительно 125°. [7]

Процесс трансформации джиттербага

Бакминстер Фуллер обнаружил, что кубооктаэдр — единственный многогранник, в котором расстояние между его центром и вершиной такое же, как и расстояние между его ребрами. Другими словами, он имеет одинаковые векторы длины в трехмерном пространстве, известные как векторное равновесие . [8] Жесткие распорки и гибкие вершины кубооктаэдра также могут быть постепенно преобразованы в правильный икосаэдр , правильный октаэдр, правильный тетраэдр. Фуллер назвал это преобразованием джиттербага . [9]

Кубооктаэдр обладает свойством Руперта , означающим, что существует многогранник такого же или большего размера, который может пройти через его отверстие. [10]

Симметрия и классификация

3D модель кубооктаэдра

Кубооктаэдр является архимедовым телом , то есть это высокосимметричный и полуправильный многогранник, и две или более различных правильных многоугольных граней сходятся в вершине. [11] Кубооктаэдр имеет две симметрии, вытекающие из построений, как было упомянуто выше: та же симметрия, что и у правильного октаэдра или куба, октаэдрическая симметрия , и та же симметрия, что и у правильного тетраэдра, тетраэдрическая симметрия . [12] Многоугольные грани, которые сходятся для каждой вершины, представляют собой два равносторонних треугольника и два квадрата, а вершинная фигура кубооктаэдра равна 3.4.3.4. Двойственным кубооктаэдру является ромбический додекаэдр . [13] О час {\displaystyle \mathrm {O} _ {\mathrm {h} }} Т г {\ displaystyle \ mathrm {T} _ {\ mathrm {d} }}

Радиальная равносторонняя симметрия

В кубооктаэдре длинный радиус (от центра до вершины) равен длине ребра; таким образом, его длинный диаметр (от вершины до противоположной вершины) равен 2 длинам ребра. [14] Его центр подобен вершине канонической пирамиды: на расстоянии одной длины ребра от всех остальных вершин. (В случае кубооктаэдра центр на самом деле является вершиной 6 квадратных и 8 треугольных пирамид). Эта радиальная равносторонняя симметрия является свойством только нескольких однородных многогранников , включая двумерный шестиугольник , трехмерный кубооктаэдр и четырехмерные 24-ячейковый и 8-ячейковый (тессеракт) . [15] Радиально равносторонние многогранники — это те, которые могут быть построены с их длинными радиусами из равносторонних треугольников, которые встречаются в центре многогранника, каждый из которых вносит два радиуса и ребро. Следовательно, все внутренние элементы, которые встречаются в центре этих многогранников, имеют внутренние грани в виде равносторонних треугольников, как при разбиении кубооктаэдра на 6 квадратных пирамид и 8 тетраэдров.

Каждый из этих радиально равносторонних многогранников также встречается в виде ячеек характерной заполняющей пространство мозаики : мозаики правильных шестиугольников, выпрямленных кубических сот (из чередующихся кубооктаэдров и октаэдров), 24-ячеистых сот и тессерактовых сот , соответственно. [16] Каждая мозаика имеет двойную мозаику ; центры ячеек в мозаике являются вершинами ячеек в ее двойной мозаике. Самая плотная известная правильная упаковка сфер в двух, трех и четырех измерениях использует центры ячеек одной из этих мозаик в качестве центров сфер.

Поскольку кубооктаэдр является радиально равносторонним, его центр находится на расстоянии одной длины ребра от 12 вершин.

Кубооктаэдр, кубогемиоктаэдр и октагемиоктаэдр .

Кубооктаэдр делит свой скелет с двумя невыпуклыми однородными многогранниками , кубогемиоктаэдром и октагемиоктаэдром . Эти многогранники построены из скелета кубооктаэдра, в котором четыре шестиугольные плоскости делят пополам его диагональ, пересекая его внутреннюю часть. Добавление шести квадратов или восьми равносторонних треугольников приводит к кубогемикотаэдру или октагемиоктаэдру соответственно. [17]

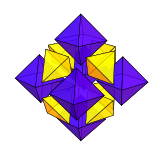
Кубооктаэдр 2-покрывает тетрагемигексаэдр , который соответственно имеет ту же абстрактную вершинную фигуру (два треугольника и два квадрата: ) и половину вершин, ребер и граней. (Фактическая вершинная фигура тетрагемигексаэдра равна , с множителем , обусловленным крестом.) [18] 3 ⋅ 4 ⋅ 3 ⋅ 4 {\displaystyle 3\cdot 4\cdot 3\cdot 4} 3 ⋅ 4 ⋅ 3 2 ⋅ 4 {\textstyle 3\cdot 4\cdot {\frac {3}{2}}\cdot 4} а 2 {\textstyle {\frac {a}{2}}}

Разбиение на квадратные пирамиды и тетраэдры

Кубооктаэдр можно разбить на 6 квадратных пирамид и 8 тетраэдров , встречающихся в центральной точке. Это разбиение выражается в тетраэдрально-октаэдрических сотах , где пары квадратных пирамид объединены в октаэдры . [19]

График

Граф кубооктаэдра

Скелет кубооктаэдра можно представить в виде графа , одного из архимедовых графов . Он имеет 12 вершин и 24 ребра. Это квартикальный граф , который представляет собой четыре вершины, соединяющие каждую вершину. [20]

Граф кубооктаэдра может быть построен как линейный граф куба, что делает его локально линейным графом . [21]

Появление

Кубооктаэдр, вероятно, был известен Платону : в «Определениях » Герона цитируются слова Архимеда о том, что Платон знал о теле, состоящем из 8 треугольников и 6 квадратов. [22]

Ссылки

Сноски

  1. ↑ Coxeter 1973, стр. 18–19, §2.3 Квазиправильные многогранники.
  2. ^
    • Берман 1971
    • Огиевецкий и Шлосман 2021, стр. 477
  3. ^ ван Леувен, Freixa & Cano 2023, стр. 50.
  4. ^ Линти 2013, стр. 41.
  5. ^ Берман 1971.
  6. ^ Коксетер 1973, стр. 52, §3.7 Координаты вершин правильных и квазиправильных тел.
  7. ↑ Джонсон 1966.
  8. ^ Кокрам 2020, стр. 53.
  9. ^ Верхейен 1989.
  10. ^ Чай, Юань и Замфиреску 2018.
  11. ^ Диудеа 2018, стр. 39.
  12. ^
    • Коджа и Коджа (2013), стр. 48
    • Кромвель (1997). Для октаэдрической симметрии см. стр. 378, рисунок 10.13. Для тетраэдрической симметрии см. стр. 380, рисунок 10.15.
  13. ↑ Уильямс 1979, стр. 74.
  14. ^ Коксетер 1973, стр. 69, §4.7 Другие соты.
  15. ^ Coxeter 1973, стр. 292–293, Таблица I (ii): столбец 0 R/l .
  16. ^ Коксетер 1973, стр. 296, Таблица II: Обычные соты.
  17. ^
    • Пизанский и Серватиус 2013, с. 108
    • Барнс 2012, стр. 53
  18. ^ Грюнбаум 2003, стр. 338.
  19. ^ Посаментье и др. 2022, с. 233–235.
  20. ↑ Рид и Уилсон 1998, стр. 269.
  21. ↑ Фан 1996.
  22. ↑ Тернболл 1931.

Цитируемые работы

  • Barnes, J. (2012). Gems of Geometry . Springer . doi :10.1007/978-3-642-30964-9. ISBN 978-3-642-30964-9.
  • Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329– 352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
  • Чай, Ин; Юань, Липин; Замфиреску, Тудор (2018). «Свойство Руперта архимедовых тел». The American Mathematical Monthly . 125 (6): 497– 504. doi :10.1080/00029890.2018.1449505. S2CID  125508192.
  • Кокрам, Бернис (2020). В фокусе Сакральная геометрия: Ваш личный гид. Wellfleet Press. ISBN 978-1-57715-225-5.
  • Коксетер, HSM (1973) [1948]. Правильные многогранники (3-е изд.). Нью-Йорк: Dover Publications .
  • Кромвель, Питер Р. (1997), Многогранники, Cambridge University Press , ISBN 978-0-521-55432-9
  • Diudea, MV (2018). Многослойные полиэдральные кластеры. Углеродные материалы: химия и физика. Том 10. Springer . doi :10.1007/978-3-319-64123-2. ISBN 978-3-319-64123-2.
  • Fan, Cong (1996). «Об обобщенных клетках». Журнал теории графов . 23 (1): 21– 31. doi :10.1002/(SICI)1097-0118(199609)23:1<21::AID-JGT2>3.0.CO;2-M. MR  1402135.
  • Ghyka, Matila (1977). Геометрия искусства и жизни ([Nachdr.] ред.). Нью-Йорк: Dover Publications . стр. 51–56, 81–84. ISBN 9780486235424.
  • Грюнбаум, Бранко (2003).«Новые» однородные многогранники». В Bezdek, Andras (ред.). Дискретная геометрия . CRC Press . ISBN 9780203911211.
  • Джонсон, Норман В. (1966). «Выпуклые многогранники с правильными гранями». Канадский журнал математики . 18 : 169– 200. doi : 10.4153/cjm-1966-021-8 . MR  0185507. S2CID  122006114. Zbl  0132.14603.
  • Koca, M.; Koca, NO (2013). «Группы Кокстера, кватернионы, симметрии многогранников и 4D-политопов». Математическая физика: Труды 13-й региональной конференции, Анталья, Турция, 27–31 октября 2010 г. World Scientific.
  • Linti, G. (2013). "Catened Compounds - Group 13 [Al, Ga, In, Tl]". В Reedijk, J.; Poeppelmmeier, K. (ред.). Comprehensive Inorganic Chemistry II: From Elements to Applications . Newnes.
  • Огиевецкий, О.; Шлосман, С. (2021). «Платоновы соединения и цилиндры». В Новиков, С.; Кричевер, И.; Огиевецкий, О.; Шлосман, С. (ред.). Интегрируемость, квантование и геометрия: II. Квантовые теории и алгебраическая геометрия. Американское математическое общество . ISBN 978-1-4704-5592-7.
  • Писански, Т.; Серватиус, Б. (2013). Конфигурация с графической точки зрения. Springer. doi :10.1007/978-0-8176-8364-1. ISBN 978-0-8176-8363-4.
  • Посаментье, А.С.; Таллер, Б.; Дорнер, К.; Геретшлегер, Р.; Мареш, Г.; Шпрейцер, К.; Штулпфаррер, Д. (2022). Геометрия в нашем трехмерном мире. Всемирная научная . ISBN 978-981-12-3712-6.
  • Рид, Р. К.; Уилсон, Р. Дж. (1998). Атлас графиков . Oxford University Press .
  • Turnball, HW (1931). «Руководство по греческой математике». Nature . 128 (3235): 739– 740. Bibcode : 1931Natur.128..739T. doi : 10.1038/128739a0. S2CID  3994109.
  • van Leeuwen, P.; Freixa, Z.; Cano, I. (2023). «Введение в хиральность». Энантиоселективные реакции формирования связей CC: с точки зрения комплексов металлов, органо- и биокатализируемых перспектив. Academic Press . ISBN 978-0-443-15774-5.
  • Верхейен, ХФ (1989). «Полный набор трансформаторов джиттербага и анализ их движения». Компьютеры и математика с приложениями . 17 ( 1– 3): 203– 250. doi :10.1016/0898-1221(89)90160-0. MR  0994201.
  • Уильямс, Роберт (1979). Геометрическая основа естественной структуры: первоисточник дизайна. Dover Publications, Inc. ISBN 978-0-486-23729-9.
  • Однородные многогранники
  • Виртуальная реальность Многогранники Энциклопедия многогранников
  • Вайсштейн, Эрик В. , «Кубоктаэдр» («Архимедово тело») на MathWorld .
  • Кубооктаэдр на Hexnet — сайте, посвященном шестиугольной математике.
  • Клитцинг, Ричард. «Трехмерные выпуклые однородные многогранники o3x4o - co».
  • Редактируемая печатная развертка кубооктаэдра с интерактивным 3D-просмотром
Взято с "https://en.wikipedia.org/w/index.php?title=Кубооктаэдр&oldid=1250202808"