Теорема Байеса

Часть серии статей о
Байесовская статистика
Апостериор = Вероятность × Априор ÷ Доказательства
Фон
Байесовский вывод Байесовская вероятность Теорема Байеса Теорема Бернштейна–фон Мизеса Слаженность Теорема Кокса Правление Кромвеля Принцип правдоподобия Принцип безразличия Принцип максимальной энтропии
Модельное строительство
Сопряженный априор Линейная регрессия Эмпирический Байес Иерархическая модель
Апостериорное приближение
Марковская цепь Монте-Карло Приближение Лапласа Интегрированные вложенные приближения Лапласа Вариационный вывод Приблизительное байесовское вычисление
Оценщики
Байесовская оценка Достоверный интервал Максимальная апостериорная оценка
Приближение доказательств
Нижняя граница доказательств Вложенная выборка
Оценка модели
Фактор Байеса ( критерий Шварца ) Усреднение модели Апостериорный предиктивный
Математический портал
в т е

Wikifunctions имеет функцию, связанную с этой темой .

Теорема Байеса (альтернативно закон Байеса или правило Байеса , в честь Томаса Байеса ) дает математическое правило для инвертирования условных вероятностей , позволяя найти вероятность причины, учитывая ее следствие. ^[1] Например, если известно, что риск развития проблем со здоровьем увеличивается с возрастом, теорема Байеса позволяет более точно оценить риск для человека известного возраста, обусловливая его относительно его возраста, а не предполагая, что человек типичен для популяции в целом. Основываясь на законе Байеса, необходимо учитывать как распространенность заболевания в данной популяции, так и частоту ошибок теста на инфекционные заболевания, чтобы оценить значение положительного результата теста и избежать ошибки базовой вероятности .

Одним из многочисленных применений теоремы Байеса является байесовский вывод , подход к статистическому выводу , где он используется для инвертирования вероятности наблюдений при заданной конфигурации модели (т. е. функции правдоподобия ) для получения вероятности конфигурации модели при заданных наблюдениях (т. е. апостериорной вероятности ).

Теорема Байеса названа в честь Томаса Байеса ( / b eɪ z / ), министра, статистика и философа. Байес использовал условную вероятность для предоставления алгоритма (его Предложение 9), который использует доказательства для вычисления пределов неизвестного параметра. Его работа была опубликована в 1763 году как Эссе о решении проблемы в доктрине шансов . Байес изучал, как вычислить распределение для параметра вероятности биномиального распределения (в современной терминологии). После смерти Байеса его семья передала его работы другу, министру, философу и математику Ричарду Прайсу .

Прайс значительно редактировал неопубликованную рукопись в течение двух лет, прежде чем отправить ее другу, который прочитал ее вслух в Королевском обществе 23 декабря 1763 года. ^[2] Прайс отредактировал ^[3] основную работу Байеса «Эссе о решении проблемы в доктрине случайностей» (1763), которая появилась в Philosophical Transactions , ^[4] и содержит теорему Байеса. Прайс написал введение к статье, в котором излагаются некоторые философские основы байесовской статистики , и выбрал одно из двух решений, предложенных Байесом. В 1765 году Прайс был избран членом Королевского общества в знак признания его работы над наследием Байеса. ^{[5] [6]} 27 апреля в Королевском обществе было зачитано и позже опубликовано письмо, отправленное его другу Бенджамину Франклину , в котором Прайс применяет эту работу к населению и вычислению «пожизненных рент». ^[7]

Независимо от Байеса, Пьер-Симон Лаплас использовал условную вероятность для формулирования отношения обновленной апостериорной вероятности к априорной вероятности, при наличии доказательств. Он воспроизвел и расширил результаты Байеса в 1774 году, по-видимому, не зная о работе Байеса, в 1774 году и обобщил его результаты в Théorie analytique des probabilités (1812). ^{[примечание 1] [8]} Байесовская интерпретация вероятности была разработана в основном Лапласом. ^[9]

Примерно 200 лет спустя сэр Гарольд Джеффрис положил алгоритм Байеса и формулировку Лапласа на аксиоматическую основу, написав в книге 1973 года, что теорема Байеса «является для теории вероятностей тем же, чем теорема Пифагора является для геометрии» ^[10] .

Стивен Стиглер использовал байесовский аргумент, чтобы заключить, что теорема Байеса была открыта Николасом Сондерсоном , слепым английским математиком, за некоторое время до Байеса, ^{[11] [12],} но это оспаривается. ^[13] Мартин Хупер ^[14] и Шэрон Макгрейн ^[15] утверждают, что вклад Ричарда Прайса был существенным:

По современным стандартам, мы должны ссылаться на правило Байеса-Прайса. Прайс обнаружил работу Байеса, признал ее важность, исправил ее, внес вклад в статью и нашел ей применение. Современная традиция использовать только имя Байеса несправедлива, но настолько укоренилась, что все остальное не имеет смысла. ^[15]

Теорема Байеса математически формулируется в виде следующего уравнения: ^[16]

где и — события и .${\displaystyle A}$${\displaystyle B}$${\displaystyle P(B)\neq 0}$

• ${\displaystyle P(A\vert B)}$это условная вероятность : вероятность события, происходящего при условии, что это правда. Она также называется апостериорной вероятностью данного .${\displaystyle A}$${\displaystyle B}$${\displaystyle A}$${\displaystyle B}$
• ${\displaystyle P(B\vert A)}$также является условной вероятностью: вероятность события, происходящего при условии, что это правда. Ее также можно интерпретировать как вероятность того, что задано фиксированное, поскольку .${\displaystyle B}$${\displaystyle A}$${\displaystyle A}$${\displaystyle B}$${\displaystyle P(B\vert A)=L(A\vert B)}$
• ${\displaystyle P(A)}$и являются вероятностями наблюдения и соответственно без каких-либо заданных условий; они известны как априорная вероятность и предельная вероятность .${\displaystyle P(B)}$${\displaystyle A}$${\displaystyle B}$

Теорему Байеса можно вывести из определения условной вероятности :

${\displaystyle P(A\vert B)={\frac {P(A\cap B)}{P(B)}},{\text{ if }}P(B)\neq 0,}$

где — вероятность того, что оба утверждения A и B верны. Аналогично,${\displaystyle P(A\cap B)}$

${\displaystyle P(B\vert A)={\frac {P(A\cap B)}{P(A)}},{\text{ if }}P(A)\neq 0.}$

Решая и подставляя в приведенное выше выражение, получаем теорему Байеса:${\displaystyle P(A\cap B)}$${\displaystyle P(A\vert B)}$

${\displaystyle P(A\vert B)={\frac {P(B\vert A)P(A)}{P(B)}},{\text{ if }}P(B)\neq 0.}$

Для двух непрерывных случайных величин X и Y теорема Байеса может быть аналогично выведена из определения условной плотности :

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}}$

${\displaystyle f_{Y\vert X=x}(y)={\frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

Поэтому,

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{Y\vert X=x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Пусть будет условным распределением заданного и пусть будет распределением . Совместное распределение тогда будет . Условное распределение заданного тогда определяется как${\displaystyle P_{Y}^{x}}$${\displaystyle Y}$${\displaystyle X=x}$${\displaystyle P_{X}}$${\displaystyle X}$${\displaystyle P_{X,Y}(dx,dy)=P_{Y}^{x}(dy)P_{X}(dx)}$${\displaystyle P_{X}^{y}}$${\displaystyle X}$${\displaystyle Y=y}$

$${\displaystyle P_{X}^{y}(A)=E(1_{A}(X)|Y=y)}$$

Существование и единственность необходимого условного ожидания является следствием теоремы Радона–Никодима . Она была сформулирована Колмогоровым в 1933 году. Колмогоров подчеркивает важность условной вероятности, написав: «Я хочу обратить внимание на ... теорию условных вероятностей и условных ожиданий». ^[17] Теорема Байеса определяет апостериорное распределение из априорного распределения. Уникальность требует предположений о непрерывности. ^[18] Теорему Байеса можно обобщить, включив в нее неправильные априорные распределения, такие как равномерное распределение на вещественной прямой. ^[19] Современные методы Монте-Карло для цепей Маркова повысили важность теоремы Байеса, в том числе в случаях с неправильными априорными данными. ^[20]

Правило Байеса и вычисление условных вероятностей предоставляют метод решения ряда популярных головоломок, таких как задача о трех заключенных , задача о Монти Холле , задача о двух детях и задача о двух конвертах .

Предположим, что конкретный тест на то, употреблял ли кто-то каннабис, имеет 90% чувствительности , что означает истинно положительный показатель (TPR) = 0,90. Таким образом, он приводит к 90% истинно положительных результатов (правильное определение употребления наркотиков) для пользователей каннабиса.

Тест также специфичен на 80% , что означает истинно отрицательный показатель (TNR) = 0,80. Таким образом, тест правильно определяет 80% неиспользования для непользователей, но также генерирует 20% ложноположительных результатов, или ложноположительный показатель (FPR) = 0,20, для непользователей.

Если предположить, что распространенность составляет 0,05 , то есть 5% людей употребляют каннабис, какова вероятность того , что случайный человек, у которого положительный результат теста, действительно употребляет каннабис?

Положительная прогностическая ценность (ППЦ) теста — это доля лиц, которые действительно дали положительный результат, среди всех лиц с положительным результатом теста. Ее можно рассчитать на основе выборки следующим образом:

PPV = Истинно положительный / Тест положительный

Если известны чувствительность, специфичность и распространенность, PPV можно рассчитать с помощью теоремы Байеса. Пусть означает «вероятность того, что кто-то является потребителем каннабиса, при условии, что его тест положительный», что и означает PPV. Мы можем записать:${\displaystyle P({\text{User}}\vert {\text{Positive}})}$

${\displaystyle {\begin{aligned}P({\text{User}}\vert {\text{Positive}})&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}})}}\\&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}}\\[8pt]&={\frac {0.90\times 0.05}{0.90\times 0.05+0.20\times 0.95}}={\frac {0.045}{0.045+0.19}}\approx 19\%\end{aligned}}}$

Знаменатель — это прямое применение закона полной вероятности . В этом случае он говорит, что вероятность того, что кто-то даст положительный результат, равна вероятности того, что пользователь даст положительный результат, умноженной на вероятность того, что он пользователь, плюс вероятность того, что не-пользователь даст положительный результат, умноженной на вероятность того, что он не-пользователь. Это верно, поскольку классификации «пользователь» и «не-пользователь» образуют раздел множества , а именно множества людей, которые проходят тест на наркотики. Это в сочетании с определением условной вероятности приводит к приведенному выше утверждению.${\displaystyle P({\text{Positive}})=P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}$

Другими словами, если у кого-то положительный результат теста, вероятность того, что он употребляет каннабис, составляет всего 19%, поскольку в этой группе только 5% людей употребляют его, а большинство положительных результатов являются ложноположительными, полученными от оставшихся 95%.

Если протестировать 1000 человек:

• 950 не являются пользователями и 190 из них дают ложноположительные результаты (0,20 × 950)
• 50 из них являются пользователями и 45 из них дают истинно положительный ответ (0,90 × 50)

Таким образом, у 1000 человек 235 положительных тестов, из которых только 45 являются подлинными, что составляет около 19%.

Важность специфичности можно продемонстрировать, показав, что даже если чувствительность повысить до 100%, а специфичность сохранить на уровне 80%, вероятность того, что человек с положительным результатом теста является потребителем каннабиса, возрастет только с 19% до 21%, но если чувствительность сохранить на уровне 90%, а специфичность повысить до 95%, вероятность возрастет до 49%.

Если у всех пациентов с раком поджелудочной железы есть определенный симптом, это не значит, что у любого человека с этим симптомом есть 100% шанс заболеть раком поджелудочной железы. Если предположить, что частота рака поджелудочной железы составляет 1/100000, а у 10/99999 здоровых людей во всем мире есть те же симптомы, вероятность наличия рака поджелудочной железы с учетом симптомов составляет 9,1%, а остальные 90,9% могут быть «ложноположительными» (то есть ложно заявленными о наличии рака; «положительный» — сбивающий с толку термин, когда, как в данном случае, тест дает плохие новости).

В следующей таблице представлены соответствующие цифры на 100 000 человек, основанные на уровне заболеваемости.

Что затем можно использовать для расчета вероятности наличия рака при наличии симптомов:

${\displaystyle {\begin{aligned}P({\text{Cancer}}|{\text{Symptoms}})&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}})}}\\&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})+P({\text{Symptoms}}|{\text{Non-Cancer}})P({\text{Non-Cancer}})}}\\[8pt]&={\frac {1\times 0.00001}{1\times 0.00001+(10/99999)\times 0.99999}}={\frac {1}{11}}\approx 9.1\%\end{aligned}}}$

Фабрика производит изделия с использованием трех машин — A, B и C, — которые составляют 20%, 30% и 50% ее продукции соответственно. Из изделий, произведенных машиной A, 5% являются дефектными, в то время как 3% изделий B и 1% изделий C являются дефектными. Если случайно выбранная деталь является дефектной, какова вероятность того, что она была произведена машиной C?

Опять же, ответ можно получить, не используя формулу, применив условия к гипотетическому числу случаев. Например, если фабрика производит 1000 изделий, 200 будет произведено на заводе A, 300 на заводе B и 500 на заводе C. Машина A произведет 5% × 200 = 10 дефектных изделий, B 3% × 300 = 9 и C 1% × 500 = 5, что в сумме составит 24. Таким образом, 24/1000 (2,4%) от общего объема производства будут дефектными, а вероятность того, что случайно выбранный дефектный предмет был произведен машиной C, составляет 5/24 (~20,83%).

Эту задачу можно решить также с помощью теоремы Байеса: Пусть X _i обозначает событие, что случайно выбранный элемент был изготовлен i ^-й машиной (для i  = A,B,C). Пусть Y обозначает событие, что случайно выбранный элемент является дефектным. Тогда нам дана следующая информация:

${\displaystyle P(X_{A})=0.2,\quad P(X_{B})=0.3,\quad P(X_{C})=0.5.}$

Если деталь была изготовлена ​​на первой машине, то вероятность того, что она бракованная, составляет 0,05; то есть P ( Y  |  X _A ) = 0,05. В целом, имеем

${\displaystyle P(Y|X_{A})=0.05,\quad P(Y|X_{B})=0.03,\quad P(Y|X_{C})=0.01.}$

Чтобы ответить на исходный вопрос, сначала найдем P (Y). Это можно сделать следующим образом:

${\displaystyle P(Y)=\sum _{i}P(Y|X_{i})P(X_{i})=(0.05)(0.2)+(0.03)(0.3)+(0.01)(0.5)=0.024.}$

Таким образом, 2,4% от общего объема выпускаемой продукции является бракованной.

Нам дано, что произошло событие Y , и мы хотим вычислить условную вероятность события X _C. По теореме Байеса,

${\displaystyle P(X_{C}|Y)={\frac {P(Y|X_{C})P(X_{C})}{P(Y)}}={\frac {0.01\cdot 0.50}{0.024}}={\frac {5}{24}}}$

Учитывая, что деталь неисправна, вероятность того, что она была изготовлена ​​машиной C, составляет 5/24. Машина C производит половину общего объема продукции, но гораздо меньшую долю дефектных деталей. Следовательно, знание того, что выбранная деталь была дефектной, позволяет нам заменить априорную вероятность P ( X _C ) = 1/2 меньшей апостериорной вероятностью P ( X _C  |  Y ) = 5/24.

Интерпретация правила Байеса зависит от интерпретации вероятности, приписываемой терминам. Ниже описаны две преобладающие интерпретации.

В байесовской (или эпистемологической) интерпретации вероятность измеряет «степень веры». Теорема Байеса связывает степень веры в предложение до и после учета доказательств. Например, предположим, что с 50% уверенностью полагают, что монета в два раза чаще выпадает орлом, чем решкой. Если монету подбросить несколько раз и наблюдать результаты, эта степень веры, вероятно, вырастет или упадет, но может остаться прежней, в зависимости от результатов. Для предложения A и доказательства B ,

• P  ( A ), априорная величина , представляет собой начальную степень веры в A.
• P  ( A  |  B ), апостериорная величина , представляет собой степень уверенности после включения новости о том, что B является правдой.
• частное ⁠П ( Б  |  А )/П ( Б )⁠ представляет собой поддержку, которую B оказывает A.

Более подробную информацию о применении теоремы Байеса при байесовской интерпретации вероятности см. в статье Байесовский вывод .

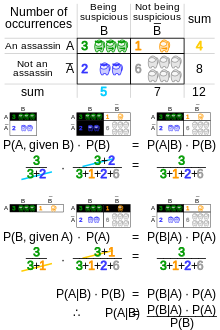
В частотной интерпретации вероятность измеряет «долю результатов». Например, предположим, что эксперимент проводится много раз. P ( A ) — это доля результатов со свойством A (априорная), а P ( B ) — это доля результатов со свойством B . P ( B  |  A ) — это доля результатов со свойством B среди результатов со свойством A , а P ( A  |  B ) — это доля результатов с A среди результатов с B (апостериорная).

Роль теоремы Байеса можно продемонстрировать с помощью древовидных диаграмм. Две диаграммы разделяют одни и те же результаты по A и B в противоположных порядках, чтобы получить обратные вероятности. Теорема Байеса связывает различные разбиения.

Энтомолог замечает, что из-за узора на спине может быть редким подвидом жука . У 98 % членов редкого подвида есть узор, поэтому P (Узор | Редкий) = 98 %. Только 5% членов обычного подвида имеют узор. Редкий подвид составляет 0,1% от общей популяции. Насколько вероятно, что жук с узором будет редким: чему равно P (Редкий | Узор)?

Из расширенной формы теоремы Байеса (поскольку любой жук либо редок, либо обычен),

$${\displaystyle {\begin{aligned}P({\text{Rare}}\vert {\text{Pattern}})&={\frac {P({\text{Pattern}}\vert {\text{Rare}})\,P({\text{Rare}})}{P({\text{Pattern}})}}\\[8pt]&={\tfrac {P({\text{Pattern}}\vert {\text{Rare}})\,P({\text{Rare}})}{P({\text{Pattern}}\vert {\text{Rare}})\,P({\text{Rare}})+P({\text{Pattern}}\vert {\text{Common}})\,P({\text{Common}})}}\\[8pt]&={\frac {0.98\times 0.001}{0.98\times 0.001+0.05\times 0.999}}\\[8pt]&\approx 1.9\%\end{aligned}}}$$

Для событий A и B , при условии, что P ( B ) ≠ 0,

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B)}}.}$

Во многих приложениях, например, в байесовском выводе , событие B фиксируется в обсуждении, и мы хотим рассмотреть влияние его наблюдения на нашу веру в различные возможные события A. В таких ситуациях знаменатель последнего выражения, вероятность данного свидетельства B , фиксируется; то, что мы хотим изменить, это A. Теорема Байеса показывает, что апостериорные вероятности пропорциональны числителю, поэтому последнее уравнение становится следующим:

${\displaystyle P(A|B)\propto P(A)\cdot P(B|A).}$

Другими словами, апостериорная вероятность пропорциональна априорной вероятности, умноженной на вероятность. ^[21]

Если события A ₁ , A ₂ , ..., являются взаимоисключающими и исчерпывающими, т. е. одно из них обязательно произойдет, но никакие два не могут произойти вместе, мы можем определить константу пропорциональности, используя тот факт, что их вероятности должны давать в сумме единицу. Например, для данного события A само событие A и его дополнение ¬ A являются исключающими и исчерпывающими. Обозначая константу пропорциональности через c , мы имеем:

${\displaystyle P(A|B)=c\cdot P(A)\cdot P(B|A){\text{ and }}P(\neg A|B)=c\cdot P(\neg A)\cdot P(B|\neg A).}$

Сложив эти две формулы, получаем, что:

${\displaystyle 1=c\cdot (P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)),}$

или

${\displaystyle c={\frac {1}{P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)}}={\frac {1}{P(B)}}.}$

Другая форма теоремы Байеса для двух конкурирующих утверждений или гипотез выглядит следующим образом:

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}.}$

Для эпистемологической интерпретации:

Для предложения A и доказательства или фона B , ^[22]

• ${\displaystyle P(A)}$априорная вероятность , начальная степень веры в А.
• ${\displaystyle P(\neg A)}$— это соответствующая начальная степень веры в не-А , в то, что А ложно, где${\displaystyle P(\neg A)=1-P(A)}$
• ${\displaystyle P(B|A)}$— это условная вероятность или правдоподобие, степень веры в B при условии, что A истинно.
• ${\displaystyle P(B|\neg A)}$— это условная вероятность или правдоподобие, степень веры в B при условии, что A ложно.
• ${\displaystyle P(A|B)}$апостериорная вероятность , вероятность события A после учета события B.

Часто для некоторого разбиения { A _j } пространства выборки пространство событий задается в терминах P ( A _j ) и P ( B  |  A _j ). Тогда полезно вычислить P ( B ) с помощью закона полной вероятности :

${\displaystyle P(B)=\sum _{j}P(B\cap A_{j}),}$

Или (используя правило умножения для условной вероятности), ^[23]

${\displaystyle P(B)={\sum _{j}P(B|A_{j})P(A_{j})},}$

${\displaystyle \Rightarrow P(A_{i}|B)={\frac {P(B|A_{i})P(A_{i})}{\sum \limits _{j}P(B|A_{j})P(A_{j})}}\cdot }$

В частном случае, когда A — двоичная переменная :

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}\cdot }$

Рассмотрим выборочное пространство Ω, сгенерированное двумя случайными величинами X и Y с известными распределениями вероятностей. В принципе, теорема Байеса применима к событиям A  = { X  =  x } и B  = { Y  =  y }.

${\displaystyle P(X{=}x|Y{=}y)={\frac {P(Y{=}y|X{=}x)P(X{=}x)}{P(Y{=}y)}}}$

Члены становятся равными 0 в точках, где любая из переменных имеет конечную плотность вероятности . Чтобы оставаться полезной, теорему Байеса можно сформулировать в терминах соответствующих плотностей (см. Вывод).

Если X непрерывен, а Y дискретен,

${\displaystyle f_{X|Y{=}y}(x)={\frac {P(Y{=}y|X{=}x)f_{X}(x)}{P(Y{=}y)}}}$

где каждая из них является функцией плотности.${\displaystyle f}$

Если X дискретен, а Y непрерывен,

${\displaystyle P(X{=}x|Y{=}y)={\frac {f_{Y|X{=}x}(y)P(X{=}x)}{f_{Y}(y)}}.}$

Если и X, и Y непрерывны,

${\displaystyle f_{X|Y{=}y}(x)={\frac {f_{Y|X{=}x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Непрерывное пространство событий часто концептуализируется в терминах числителя. Тогда полезно исключить знаменатель, используя закон полной вероятности . Для f _Y ( y ) это становится интегралом:

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }f_{Y|X=\xi }(y)f_{X}(\xi )\,d\xi .}$

Теорема Байеса в форме коэффициентов выглядит следующим образом:

${\displaystyle O(A_{1}:A_{2}\vert B)=O(A_{1}:A_{2})\cdot \Lambda (A_{1}:A_{2}\vert B)}$

где

${\displaystyle \Lambda (A_{1}:A_{2}\vert B)={\frac {P(B\vert A_{1})}{P(B\vert A_{2})}}}$

называется коэффициентом Байеса или отношением правдоподобия . Шансы между двумя событиями — это просто отношение вероятностей двух событий. Таким образом:

${\displaystyle O(A_{1}:A_{2})={\frac {P(A_{1})}{P(A_{2})}},}$

${\displaystyle O(A_{1}:A_{2}\vert B)={\frac {P(A_{1}\vert B)}{P(A_{2}\vert B)}},}$

Таким образом, правило гласит, что апостериорные шансы равны априорным шансам, умноженным на фактор Байеса ; другими словами, апостериорные шансы пропорциональны априорным шансам, умноженным на вероятность.

В частном случае, когда и , пишут , и используют аналогичное сокращение для фактора Байеса и для условных шансов. Шансы по определению являются шансами за и против . Правило Байеса тогда можно записать в сокращенной форме${\displaystyle A_{1}=A}$${\displaystyle A_{2}=\neg A}$${\displaystyle O(A)=O(A:\neg A)=P(A)/(1-P(A))}$${\displaystyle A}$${\displaystyle A}$

${\displaystyle O(A\vert B)=O(A)\cdot \Lambda (A\vert B),}$

или, говоря словами, апостериорные шансы на равны априорным шансам на умножить на отношение правдоподобия для данной информации . Короче говоря, апостериорные шансы равны априорным шансам на умножить на отношение правдоподобия .${\displaystyle A}$${\displaystyle A}$${\displaystyle A}$${\displaystyle B}$

Например, если медицинский тест имеет чувствительность 90% и специфичность 91%, то положительный байесовский фактор равен . Теперь, если распространенность этого заболевания составляет 9,09%, и если мы возьмем это в качестве априорной вероятности, то априорные шансы составят около 1:10. Таким образом, после получения положительного результата теста апостериорные шансы наличия заболевания станут 1:1, что означает, что апостериорная вероятность наличия заболевания составит 50%. Если провести второй тест в последовательном тестировании, и он также окажется положительным, то апостериорные шансы наличия заболевания станут 10:1, что означает апостериорную вероятность около 90,91%. Отрицательный байесовский фактор можно рассчитать как 91%/(100%-90%)=9,1, поэтому, если второй тест окажется отрицательным, то апостериорные шансы наличия заболевания составят 1:9,1, что означает апостериорную вероятность около 9,9%.${\displaystyle \Lambda _{+}=P({\text{True Positive}})/P({\text{False Positive}})=90\%/(100\%-91\%)=10}$

Пример выше можно также понять с помощью более надежных цифр: предположим, что пациент, проходящий тест, входит в группу из 1000 человек, 91 из которых имеют заболевание (распространенность 9,1%). Если все 1000 пройдут тест, 82 из тех, у кого есть заболевание, получат истинно положительный результат (чувствительность 90,1%), 9 из тех, у кого есть заболевание, получат ложноотрицательный результат ( ложноотрицательный процент 9,9%), 827 из тех, у кого нет заболевания, получат истинно отрицательный результат (специфичность 91,0%), и 82 из тех, у кого нет заболевания, получат ложноположительный результат (ложноположительный процент 9,0%). До прохождения любого теста вероятность наличия заболевания у пациента составляет 91:909. После получения положительного результата вероятность наличия заболевания у пациента составляет

${\displaystyle {\frac {91}{909}}\times {\frac {90.1\%}{9.0\%}}={\frac {91\times 90.1\%}{909\times 9.0\%}}=1:1}$

что согласуется с тем фактом, что в группе из 1000 человек имеется 82 истинно положительных результата и 82 ложноположительных результата.

Там, где определена условная вероятность , можно увидеть, что она фиксирует импликацию . Тогда вероятностное исчисление отражает или даже обобщает различные правила логического вывода. Помимо, например, назначения бинарных значений истинности, здесь присваиваются значения вероятности утверждениям. Утверждение фиксируется утверждением , т. е. что условная вероятность принимает экстремальное значение вероятности . Аналогично, утверждение отрицания импликации фиксируется назначением . ^[1] Так, например, если , то (если оно определено) , что влечет за собой , введение импликации в логику.${\displaystyle P(A\vert B)}$${\displaystyle B\to A}$${\displaystyle B\to A}$${\displaystyle P(A\vert B)=1}$${\displaystyle 1}$${\displaystyle 0}$${\displaystyle P(A)=1}$${\displaystyle P(A\vert B)=1}$${\displaystyle A\to (B\to A)}$

Аналогично, поскольку произведение двух вероятностей, равных друг другу, требует, чтобы оба фактора также были , то можно обнаружить, что теорема Байеса${\displaystyle 1}$${\displaystyle 1}$

${\displaystyle P(A)\,P(B\vert A)=P(B)\,P(A\vert B)}$

влечет за собой , что теперь также включает в себя modus ponens .${\displaystyle {\big (}A\land (A\to B){\big )}\leftrightarrow {\big (}B\land (B\to A){\big )}}$

Для положительных значений , если оно равно , то две условные вероятности также равны, и наоборот. Обратите внимание, что это отражает общедопустимое .${\displaystyle P(A)}$${\displaystyle P(B)}$${\displaystyle (A\leftrightarrow B)\leftrightarrow {\big (}(A\to B)\leftrightarrow (B\to A){\big )}}$

С другой стороны, рассуждение о том, что любая из вероятностей классически равна, влечет за собой следующую контрапозитивную форму вышеизложенного: .${\displaystyle 0}$ ${\displaystyle {\big (}\neg B\lor \neg (B\to A){\big )}\leftrightarrow {\big (}\neg A\lor \neg (A\to B){\big )}}$

Теорема Байеса с отрицанием дает${\displaystyle A}$

${\displaystyle P(B\vert \neg A){\big (}1-P(A){\big )}={\big (}1-P(A\vert B){\big )}P(B)}$.

Исключая крайний случай (т.е. ), имеем и, в частности,${\displaystyle P(\neg A)=0}$${\displaystyle P(A)=1}$${\displaystyle P(B\vert \neg A)=P(B)\cdot {\tfrac {1-P(A\vert B)}{1-P(A)}}}$

${\displaystyle P(\neg B\vert \neg A)=1-P(B)\cdot {\frac {1-P(A\vert B)}{1-P(A)}}}$.

Исключая также экстремальный случай , можно обнаружить, что они достигают максимума одновременно:${\displaystyle P(B)=0}$${\displaystyle 1}$

${\displaystyle P(A\vert B)=1\ \leftrightarrow \ P(\neg B\vert \neg A)=1}$

который (по крайней мере, при исключении взрывных антецедентов) отражает классический принцип противопоставления

${\displaystyle (B\to A)\leftrightarrow (\neg A\to \neg B)}$.

Теорема Байеса представляет собой частный случай вывода инвертированных условных мнений в субъективной логике, выраженный как:

${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})=(\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S}){\widetilde {\phi }}a_{A},}$

где обозначает оператор инвертирования условных мнений. Аргумент обозначает пару биномиальных условных мнений, заданных источником , а аргумент обозначает априорную вероятность (иначе говоря, базовую ставку ) . Пара производных инвертированных условных мнений обозначается . Условное мнение обобщает вероятностное условное , т. е. в дополнение к назначению вероятности источник может назначить любое субъективное мнение условному утверждению . Биномиальное субъективное мнение — это убеждение в истинности утверждения со степенями эпистемической неопределенности, как выражено источником . Каждое субъективное мнение имеет соответствующую прогнозируемую вероятность . Применение теоремы Байеса к прогнозируемым вероятностям мнений является гомоморфизмом , что означает, что теорему Байеса можно выразить в терминах прогнозируемых вероятностей мнений:${\displaystyle {\widetilde {\phi }}}$${\displaystyle (\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S})}$${\displaystyle S}$${\displaystyle a_{A}}$${\displaystyle A}$${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})}$${\displaystyle \omega _{A\vert B}^{S}}$${\displaystyle P(A\vert B)}$${\displaystyle S}$${\displaystyle (A\vert B)}$${\displaystyle \omega _{A}^{S}}$${\displaystyle A}$${\displaystyle S}$${\displaystyle P(\omega _{A}^{S})}$

${\displaystyle P(\omega _{A{\tilde {|}}B}^{S})={\frac {P(\omega _{B\vert A}^{S})a(A)}{P(\omega _{B\vert A}^{S})a(A)+P(\omega _{B\vert \lnot A}^{S})a(\lnot A)}}.}$

Следовательно, субъективная теорема Байеса представляет собой обобщение теоремы Байеса. ^[24]

Версия теоремы Байеса для трех событий ^[25] получается путем добавления третьего события , на котором все вероятности обусловлены:${\displaystyle C}$${\displaystyle P(C)>0,}$

${\displaystyle P(A\vert B\cap C)={\frac {P(B\vert A\cap C)\,P(A\vert C)}{P(B\vert C)}}}$

Использование цепного правила

${\displaystyle P(A\cap B\cap C)=P(A\vert B\cap C)\,P(B\vert C)\,P(C)}$

И, с другой стороны,

${\displaystyle P(A\cap B\cap C)=P(B\cap A\cap C)=P(B\vert A\cap C)\,P(A\vert C)\,P(C)}$

Требуемый результат получается путем идентификации обоих выражений и решения для .${\displaystyle P(A\vert B\cap C)}$

В генетике правило Байеса может быть использовано для оценки вероятности того, что кто-то имеет определенный генотип. Многие люди стремятся оценить свои шансы быть затронутыми генетическим заболеванием или вероятность быть носителем интересующего их рецессивного гена. Байесовский анализ может быть выполнен на основе семейной истории или генетического тестирования, чтобы предсказать, разовьется ли у кого-то заболевание или передаст ли оно его своим детям. Генетическое тестирование и прогнозирование распространены среди пар, которые планируют иметь детей, но обеспокоены тем, что они оба могут быть носителями заболевания, особенно в сообществах с низкой генетической дисперсией. ^[26]

Пример таблицы байесовского анализа для риска заболевания у женщины на основе знания того, что заболевание присутствует у ее братьев и сестер, но не у ее родителей или любого из ее четырех детей. Основываясь исключительно на статусе братьев и сестер и родителей субъекта, она с одинаковой вероятностью может быть носителем, как и неносителем (эта вероятность обозначена априорной гипотезой). Вероятность того, что все четыре сына субъекта будут здоровы, составляет 1/16 ( 1 ⁄ 2 ⋅ 1 ⁄ 2 ⋅ 1 ⁄ 2 ⋅ 1 ⁄ 2 ), если она является носителем, и около 1, если она не является носителем (это условная вероятность). Совместная вероятность согласовывает эти два прогноза, умножая их друг на друга. Последняя строка (апостериорная вероятность) рассчитывается путем деления совместной вероятности для каждой гипотезы на сумму обеих совместных вероятностей. ^[27]

Генетическое тестирование родителей может обнаружить около 90% известных аллелей болезней у родителей, которые могут привести к носительству или поражению у их детей. Муковисцидоз — это наследственное заболевание, вызванное аутосомно-рецессивной мутацией в гене CFTR, ^[28] расположенном на плече q хромосомы 7. ^[29]

Вот байесовский анализ пациентки с семейным анамнезом муковисцидоза (МВ), которая дала отрицательный результат на МВ, демонстрирующий, как этот метод использовался для определения риска рождения ребенка с МВ: поскольку пациентка не поражена, она либо гомозиготна по аллелю дикого типа, либо гетерозиготна. Для установления априорных вероятностей используется квадрат Паннета, основанный на знании того, что ни один из родителей не был поражен болезнью, но оба могли быть носителями:

Учитывая, что пациент не поражен, есть только три возможности. В пределах этих трех есть два сценария, в которых пациент является носителем мутантного аллеля. Таким образом, априорные вероятности составляют 2 ⁄ 3 и 1 ⁄ 3 .

Далее пациент проходит генетическое тестирование и получает отрицательный результат на муковисцидоз. Этот тест имеет 90%-ную точность обнаружения, поэтому условные вероятности отрицательного теста составляют 1/10 и 1. Наконец, как и прежде, вычисляются совместная и апостериорная вероятности.

После проведения того же анализа в отношении партнера-мужчины пациентки (с отрицательным результатом теста) вероятность того, что их ребенок будет болен, равна произведению соответствующих апостериорных вероятностей того, что родители являются носителями, на вероятность того, что двое носителей произведут больного ребенка ( 1 ⁄ 4 ).

Байесовский анализ можно выполнить с использованием фенотипической информации, связанной с генетическим состоянием. В сочетании с генетическим тестированием этот анализ становится намного сложнее. Например, кистозный фиброз можно обнаружить у плода с помощью ультразвука, который ищет эхогенный кишечник, который выглядит ярче, чем обычно при сканировании. Это не надежный тест, так как эхогенный кишечник может присутствовать у совершенно здорового плода. Генетическое тестирование родителей очень влиятельно в этом случае, где фенотипический аспект может быть чрезмерно влиятельным при расчете вероятности. В случае плода с эхогенным кишечником, с матерью, которая была протестирована и, как известно, является носителем муковисцидоза, апостериорная вероятность того, что у плода есть это заболевание, очень высока (0,64). Но как только отец получает отрицательный результат теста на муковисцидоз, апостериорная вероятность значительно падает (до 0,16). ^[27]

Расчет фактора риска является мощным инструментом в генетическом консультировании и репродуктивном планировании, но его нельзя рассматривать как единственный важный фактор. Как и выше, неполное тестирование может дать ложно высокую вероятность статуса носителя, а тестирование может быть финансово недоступным или неосуществимым, если родитель не присутствует.

• Байесовская эпистемология
• Индуктивная вероятность
• Квантовый байесианизм
• Почему большинство опубликованных результатов исследований ложны , эссе 2005 года по метанауке Джона Иоаннидиса
• Обычная условная вероятность
• Байесовское убеждение

•  В этой статье использован текст из публикации, которая сейчас находится в общественном достоянии :  Митчелл, Джон Малкольм (1911). «Прайс, Ричард». В книге Чисхолма, Хью (ред.). Encyclopaedia Britannica . Том 22 (11-е изд.). Cambridge University Press. С.  314–315 .

• Болстад, Уильям М.; Карран, Джеймс М. (2017). «Логика, вероятность и неопределенность». Введение в байесовскую статистику (3-е изд.). Нью-Йорк: Wiley. С.  59–82 . ISBN 978-1-118-09156-2.
• Ли, Питер М. (2012). Байесовская статистика: Введение (4-е изд.). Wiley. ISBN 978-1-118-33257-3.
• Шмитт, Сэмюэл А. (1969). «Накопление доказательств». Измерение неопределенности: элементарное введение в байесовскую статистику . Чтение: Addison-Wesley. стр.  61–99 . OCLC  5013.
• Стиглер, Стивен М. (август 1986 г.). «Мемуары Лапласа 1774 года об обратной вероятности». Статистическая наука . 1 (3): 359– 363. doi : 10.1214/ss/1177013620 .

• «Байесовская ловушка». Veritasium . 5 апреля 2017 г. – через YouTube .