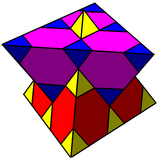
Треугольные трапециевидные соты

Заполняющая пространство тесселяция

Треугольные трапециевидные соты

Тип	Двойные однородные соты
Диаграммы Коксетера-Дынкина
Клетка	Тригональный трапецоэдр (1/4 ромбододекаэдра )
Лица	Ромб
Космическая группа	$Фд 3 м (227)$
Группа Коксетера	${\тильда {A}}_{3}$ $3 [4]$ (двойной)
вершинные фигуры	\|
Двойной	Четверть кубических сот
Характеристики	Клеточно-транзитивный , Face-транзитивный

В геометрии тригональные трапецоэдрические соты — это равномерно заполняющая пространство мозаика (или соты ) в евклидовом 3-мерном пространстве . Ячейки — это идентичные тригональные трапецоэдры или ромбоэдры . Конвей, Бергил и Гудман-Штраус называют это сплющенным кубиллом . ^[1]

Связанные соты и плитки

Эти соты можно рассматривать как ромбододекаэдрические соты , в которых ромбододекаэдры разделены центром на 4 треугольных трапецоэдра или ромбоэдра .

ромбические додекаэдрические соты	Разрез ромбододекаэдра	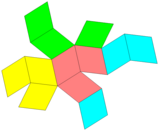Ромбическая сетка

Это аналогично тому, как правильный шестиугольник можно разбить на 3 ромба и замостить плоскость как ромб . Замостить ромбом на самом деле является ортогональной проекцией тригональных трапециевидных сот . Другая ортогональная проекция создает кадриль , в котором ромбы искажены в квадраты.

Двойная плитка

Он является дуальным по отношению к четвертькубическим сотам с тетраэдрическими и усеченными тетраэдрическими ячейками:

Смотрите также

Архитектоническая и катоптрическая мозаика

Ссылки

^ Конвей, Джон Х .; Берджил, Хайди; Гудман-Штраус, Хаим (2008), Симметрии вещей, Уэллсли, Массачусетс: AK Peters, стр. 294, ISBN 978-1-56881-220-5, МР 2410150

[1] Конвей, Джон Х .; Берджил, Хайди; Гудман-Штраус, Хаим (2008), Симметрии вещей, Уэллсли, Массачусетс: AK Peters, стр. 294, ISBN 978-1-56881-220-5, МР 2410150