Тетрагональные двуклиновидные соты

Тетрагональные двуклиновидные тетраэдрические соты
Тип	выпуклый однородный сотовый двойной
Диаграмма Коксетера-Дынкина
Тип ячейки	Тетрагональный двуклиновидный
Типы лица	равнобедренный треугольник {3}
Вершинная фигура	тетракисгексаэдр
Космическая группа	Мне 3 м (229)
Симметрия	[[4, 3, 4]]
Группа Коксетера	${\displaystyle {\тильда {C}}_{3}}$, [4, 3, 4]
Двойной	Усеченные кубические соты
Характеристики	ячейково-транзитивный , гране-транзитивный , вершинно-транзитивный

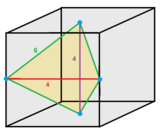
Тетрагональные дисфеноидные тетраэдрические соты — это заполняющая пространство мозаика (или соты ) в евклидовом 3-мерном пространстве, состоящая из идентичных тетрагональных дисфеноидальных ячеек. Ячейки являются гранетранзитивными с 4 идентичными равнобедренными треугольными гранями. Джон Хортон Конвей называет это сплющенным тетраэдриллом или сокращенно обтетраэдриллом . ^[1]

Ячейку можно рассматривать как 1/12 трансляционного куба, вершины которого центрированы на двух гранях и двух ребрах. Четыре его ребра принадлежат 6 ячейкам, а два ребра принадлежат 4 ячейкам.

Тетраэдрические двуклиновидные соты являются двойственными по отношению к однородным битусеченным кубическим сотам .

Его вершины образуют A^*
₃/ Д^*
₃решетка, которая также известна как объемно-центрированная кубическая решетка.

Вершинная фигура этой соты — тетракис-куб : в каждой вершине сходятся 24 двуклиноида. Объединение этих 24 двуклиноидов образует ромбический додекаэдр . Каждое ребро мозаики окружено либо четырьмя, либо шестью двуклиноидами, в зависимости от того, образует ли оно основание или одну из сторон смежных равнобедренных треугольных граней соответственно. Когда ребро образует основание смежных равнобедренных треугольников и окружено четырьмя двуклиноидами, они образуют неправильный октаэдр . Когда ребро образует одну из двух равных сторон смежных равнобедренных треугольных граней, шесть двуклиноидов, окружающих ребро, образуют особый тип параллелепипеда, называемый тригональным трапецоэдром .

Ориентацию тетрагональных двуклиновидных сот можно получить, начав с кубических сот , разделив их на плоскости , и (т.е. разделив каждый куб на тетраэдры-пути ), а затем сжав их вдоль главной диагонали до тех пор, пока расстояние между точками (0, 0, 0) и (1, 1, 1) не станет таким же, как расстояние между точками (0, 0, 0) и (0, 0, 1).${\displaystyle x=y}$${\displaystyle x=z}$${\displaystyle y=z}$

Гексакис кубические соты Пирамидилла [2]
Тип	Двойные однородные соты
Диаграммы Кокстера–Дынкина
Клетка	Равнобедренная квадратная пирамида
Лица	Треугольник квадрат
Пространственная группа Фибрифолдная нотация	Пм 3 м (221) 4 − :2
Группа Коксетера	${\displaystyle {\тильда {C}}_{3}}$, [4, 3, 4]
вершинные фигуры	,
Двойной	Усеченные кубические соты
Характеристики	Клеточно-транзитивный

Гексакис кубические соты — это равномерно заполняющая пространство мозаика (или соты ) в евклидовом 3-мерном пространстве. Джон Хортон Конвей называет ее пирамидиллой . ^[2]

Ячейки можно увидеть в трансляционном кубе, используя 4 вершины на одной грани и центр куба. Края окрашены в зависимости от того, сколько ячеек находится вокруг каждого из них.

Его можно рассматривать как кубические соты , в которых каждый куб разделен центральной точкой на 6 квадратных пирамидальных ячеек.

Существует два типа плоскостей граней: одна в виде квадратной мозаики , а другая в виде сплющенной треугольной мозаики , в которой половина треугольников удалена в качестве отверстий .

Плоскость мозаичного изображения
Симметрия	п4м, [4,4] (*442)	пмм, [∞,2,∞] (*2222)

Она двойственна усеченным кубическим сотам с октаэдрическими и усеченными кубическими ячейками:

Если квадратные пирамиды пирамидиллы соединить по основаниям, то получится еще одна сота с идентичными вершинами и ребрами, называемая квадратной бипирамидальной сотой или двойственной по отношению к выпрямленной кубической соте .

Это аналогично двумерной мозаике тетракис-квадрата :

Квадратно-бипирамидальная сота. Сплюснутый октаэдр [2]
Тип	Двойные однородные соты
Диаграммы Кокстера–Дынкина
Клетка	Квадратная бипирамида
Лица	Треугольники
Пространственная группа Фибрифолдная нотация	Пм 3 м (221) 4 − :2
Группа Коксетера	${\displaystyle {\тильда {C}}_{3}}$, [4,3,4]
вершинные фигуры	,
Двойной	Ректифицированные кубические соты
Характеристики	Клеточно-транзитивный , Face-транзитивный

Квадратные бипирамидальные соты — это равномерная заполняющая пространство мозаика (или соты ) в евклидовом 3-мерном пространстве. Джон Хортон Конвей называет ее сплющенным октаэдриллом или сокращенно — обооктаэдриллом . ^[1]

Ячейку можно увидеть расположенной внутри трансляционного куба с 4 вершинами посередине ребра и 2 вершинами на противоположных гранях. Ребра окрашены и помечены по количеству ячеек вокруг ребра.

Его можно рассматривать как кубические соты , в которых каждый куб разделен центральной точкой на 6 ячеек квадратных пирамид . Исходные стенки кубических сот удаляются, соединяя пары квадратных пирамид в квадратные бипирамиды (октаэдры). Его вершинный и рёберный каркас идентичен гексакисным кубическим сотам .

Существует один тип плоскости с гранями: сплющенная треугольная мозаика с половиной треугольников в качестве отверстий . Они разрезают грани-диагонали через исходные кубы. Существуют также квадратные плоскости мозаики, которые существуют как негранные отверстия, проходящие через центры октаэдрических ячеек.

Плоскость мозаичного изображения	Квадратная плитка "отверстия"	сплющенная треугольная мозаика
Симметрия	п4м, [4,4] (*442)	пмм, [∞,2,∞] (*2222)

Она является дуальной по отношению к выпрямленным кубическим сотам с октаэдрическими и кубооктаэдрическими ячейками:

Филликовые дисфеноидальные соты Восьмая пирамидка [3]
(Нет изображения)
Тип	Двойные однородные соты
Диаграммы Коксетера-Дынкина
Клетка	Филлик дисфеноидный
Лица	Ромб Треугольник
Пространственная группа Фибрифолдная нотация Нотация Коксетера	Я 3 м (229) 8 о :2 [[4,3,4]]
Группа Коксетера	[4,3,4],${\displaystyle {\тильда {C}}_{3}}$
вершинные фигуры	,
Двойной	Усеченные кубические соты
Характеристики	Клеточно-транзитивный , гранно-транзитивный

Филликовые дисфеноидальные соты — это равномерная заполняющая пространство мозаика (или соты ) в евклидовом 3-мерном пространстве. Джон Хортон Конвей называет это восьмой пирамидиллой . ^[3]

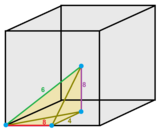
Ячейку можно рассматривать как 1/48 трансляционного куба с вершинами, расположенными: один угол, один центр ребра, один центр грани и центр куба. Цвета ребер и метки указывают, сколько ячеек существует вокруг ребра. Это одна 1/6 меньшего куба с 6 филликовыми двуклиновидными ячейками, разделяющими общую диагональную ось.

Он является дуальным по отношению к усеченным кубическим сотам :

• Архитектоническая и катоптрическая мозаика
• Кубические соты
• Пространственная рама
• Триакисы — усеченные тетраэдрические соты

• Гибб, Уильям (1990), «Бумажные шаблоны: объемные фигуры из метрической бумаги», Математика в школе , 19 (3): 2–4, перепечатано в Притчарде, Крис, ред. (2003), Изменение формы геометрии: празднование столетия геометрии и преподавания геометрии , Cambridge University Press, стр. 363–366, ISBN 0-521-53162-4.
• Сенешаль, Марджори (1981), «Какие тетраэдры заполняют пространство?», Mathematics Magazine , 54 (5), Математическая ассоциация Америки: 227–243, doi : 10.2307/2689983, JSTOR  2689983.
• Conway, John H .; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "21. Наименование архимедовых и каталонских многогранников и мозаик". Симметрии вещей . AK Peters, Ltd. стр. 292–298. ISBN 978-1-56881-220-5.