Диаграмма Вороного

В математике диаграмма Вороного — это разбиение плоскости на области , близкие к каждому из заданного набора объектов. Ее также можно классифицировать как тесселяцию . В простейшем случае эти объекты — это просто конечное число точек на плоскости (называемых семенами, сайтами или генераторами). Для каждого семени существует соответствующая область , называемая ячейкой Вороного , состоящая из всех точек плоскости, которые ближе к этому семени, чем к любой другой. Диаграмма Вороного набора точек является двойственной триангуляции Делоне этого набора .
Диаграмма Вороного названа в честь математика Георгия Вороного , а также называется мозаикой Вороного , разложением Вороного , разбиением Вороного или мозаикой Дирихле (в честь Питера Густава Лежена Дирихле ). Ячейки Вороного также известны как многоугольники Тиссена , в честь Альфреда Х. Тиссена . [1] [2] [3] Диаграммы Вороного имеют практическое и теоретическое применение во многих областях, в основном в науке и технике , но также и в изобразительном искусстве . [4] [5]
Самый простой случай
В простейшем случае, показанном на первом рисунке, нам дан конечный набор точек на евклидовой плоскости . В этом случае каждый узел является одной из этих заданных точек, а его соответствующая ячейка Вороного состоит из каждой точки на евклидовой плоскости, для которой является ближайшим узлом: расстояние до меньше или равно минимальному расстоянию до любого другого узла . Для одного другого узла точки, которые ближе к , чем к , или одинаково удалены, образуют замкнутое полупространство , граница которого является перпендикуляром к отрезку прямой . Ячейка является пересечением всех этих полупространств, и, следовательно, это выпуклый многоугольник . [6] Когда две ячейки на диаграмме Вороного имеют общую границу, это отрезок прямой , луч или линия , состоящие из всех точек на плоскости, которые равноудалены от двух их ближайших узлов. Вершины диаграммы, где встречаются три или более из этих границ, являются точками, которые имеют три или более одинаково удаленных ближайших узлов.
Формальное определение
Пусть будет метрическим пространством с функцией расстояния . Пусть будет набором индексов и пусть будет кортежем (индексированным набором) непустых подмножеств (сайтов) в пространстве . Ячейка Вороного, или область Вороного, , связанная с сайтом, — это множество всех точек, расстояние до которых не больше, чем расстояние до других сайтов , где — любой индекс, отличный от . Другими словами, если обозначает расстояние между точкой и подмножеством , то
Диаграмма Вороного — это просто кортеж ячеек . В принципе, некоторые из сайтов могут пересекаться и даже совпадать (ниже описано применение для сайтов, представляющих магазины), но обычно предполагается, что они не пересекаются. Кроме того, в определении допускается бесконечно много сайтов (эта настройка имеет приложения в геометрии чисел и кристаллографии ), но, опять же, во многих случаях рассматривается только конечное число сайтов.
В частном случае, когда пространство является конечномерным евклидовым пространством , каждый узел является точкой, имеется конечное число точек и все они различны, тогда ячейки Вороного являются выпуклыми многогранниками , и их можно представить комбинаторным способом с использованием их вершин, сторон, двумерных граней и т. д. Иногда индуцированную комбинаторную структуру называют диаграммой Вороного. Однако в общем случае ячейки Вороного могут быть невыпуклыми или даже не связанными.
В обычном евклидовом пространстве мы можем переписать формальное определение в обычных терминах. Каждый многоугольник Вороного связан с точкой-генератором . Пусть будет множеством всех точек в евклидовом пространстве. Пусть будет точкой, которая порождает свою область Вороного , которая порождает , и которая порождает , и так далее. Тогда, как выразился Тран и др . [7], «все местоположения в многоугольнике Вороного находятся ближе к точке-генератору этого многоугольника, чем любая другая точка-генератор на диаграмме Вороного на евклидовой плоскости».
Иллюстрация
В качестве простого примера рассмотрим группу магазинов в городе. Предположим, мы хотим оценить количество клиентов данного магазина. При прочих равных условиях (цена, продукты, качество обслуживания и т. д.) разумно предположить, что клиенты выбирают предпочтительный магазин просто по соображениям расстояния: они пойдут в магазин, расположенный ближе всего к ним. В этом случае ячейку Вороного данного магазина можно использовать для приблизительной оценки количества потенциальных клиентов, посещающих этот магазин (который моделируется точкой в нашем городе).
Для большинства городов расстояние между точками можно измерить с помощью известного евклидова расстояния :
или манхэттенское расстояние :
- .
Соответствующие диаграммы Вороного выглядят по-разному для разных метрик расстояния.
Характеристики
- Двойственный граф для диаграммы Вороного (в случае евклидова пространства с точечными узлами) соответствует триангуляции Делоне для того же набора точек.
- Ближайшая пара точек соответствует двум соседним ячейкам на диаграмме Вороного.
- Предположим, что задана евклидова плоскость и дискретный набор точек. Тогда две точки набора являются смежными на выпуклой оболочке тогда и только тогда, когда их ячейки Вороного имеют общую бесконечно длинную сторону.
- Если пространство является нормированным пространством и расстояние до каждого узла достигается (например, когда узел является компактным множеством или замкнутым шаром), то каждая ячейка Вороного может быть представлена как объединение отрезков прямых, исходящих из узлов. [8] Как показано там, это свойство не обязательно выполняется, когда расстояние не достигается.
- При относительно общих условиях (пространство является, возможно, бесконечномерным равномерно выпуклым пространством , может быть бесконечно много участков общей формы и т. д.) ячейки Вороного обладают определенным свойством устойчивости: небольшое изменение формы участков, например, изменение, вызванное некоторым переносом или искажением, приводит к небольшому изменению формы ячеек Вороного. Это геометрическая устойчивость диаграмм Вороного. [9] Как там показано, это свойство не выполняется в общем случае, даже если пространство двумерно (но неравномерно выпукло и, в частности, неевклидово), а участки являются точками.
История и исследования
Неформальное использование диаграмм Вороного можно проследить до Декарта в 1644 году. [10] Питер Густав Лежен Дирихле использовал двумерные и трехмерные диаграммы Вороного в своем исследовании квадратичных форм в 1850 году. Британский врач Джон Сноу использовал диаграмму, похожую на диаграмму Вороного, в 1854 году, чтобы проиллюстрировать, как большинство людей, умерших во время вспышки холеры на Брод-стрит, жили ближе к зараженному насосу на Брод-стрит, чем к любому другому водяному насосу.
Диаграммы Вороного названы в честь Георгия Феодосиевича Вороного , который определил и изучил общий n -мерный случай в 1908 году. [11] Диаграммы Вороного, которые используются в геофизике и метеорологии для анализа пространственно распределенных данных, называются полигонами Тиссена в честь американского метеоролога Альфреда Х. Тиссена , который использовал их для оценки количества осадков по разбросанным измерениям в 1911 году. Другие эквивалентные названия для этой концепции (или ее отдельных важных случаев): многогранники Вороного, многоугольники Вороного, область(и) влияния, разложение Вороного, мозаика(и) Вороного, мозаика(и) Дирихле.
Примеры

Замощения Вороного регулярных решеток точек в двух или трех измерениях приводят к появлению многих известных замощений.
- Двумерная решетка дает нерегулярную сотовую мозаику с равными шестиугольниками с точечной симметрией; в случае правильной треугольной решетки она является правильной; в случае прямоугольной решетки шестиугольники сводятся к прямоугольникам в строках и столбцах; квадратная решетка дает правильную мозаику квадратов; обратите внимание, что прямоугольники и квадраты также могут быть получены другими решетками (например, решетка, определяемая векторами (1,0) и (1/2,1/2), дает квадраты).
- Простая кубическая решетка дает кубические соты .
- Гексагональная плотноупакованная решетка дает мозаичное изображение пространства с трапециевидно-ромбическими додекаэдрами .
- Гранецентрированная кубическая решетка дает мозаичное изображение пространства с ромбическими додекаэдрами .
- Объемно -центрированная кубическая решетка дает мозаичное изображение пространства с усеченными октаэдрами .
- Параллельные плоскости с правильными треугольными решетками, выровненные по центрам друг друга, образуют шестиугольные призматические соты .
- Некоторые объемно-центрированные тетрагональные решетки создают мозаику пространства с ромбо-гексагональными додекаэдрами .
Некоторые объемно-центрированные тетрагональные решетки создают мозаику пространства с ромбо-гексагональными додекаэдрами .
Для набора точек ( x , y ), где x принадлежит дискретному множеству X , а y принадлежит дискретному множеству Y , мы получаем прямоугольные плитки с точками, не обязательно находящимися в их центрах.
Диаграммы Вороного высшего порядка
Хотя обычная ячейка Вороного определяется как множество точек, ближайших к одной точке в S , ячейка Вороного n -го порядка определяется как множество точек, имеющих определенный набор из n точек в S в качестве своих n ближайших соседей. Диаграммы Вороного более высокого порядка также подразделяют пространство.
Диаграммы Вороного более высокого порядка могут быть сгенерированы рекурсивно. Чтобы сгенерировать диаграмму Вороного n- го порядка из множества S , начните с диаграммы ( n − 1) -го порядка и замените каждую ячейку, сгенерированную X = { x 1 , x 2 , ..., x n −1 }, диаграммой Вороного, сгенерированной на множестве S − X .
Диаграмма Вороного для самой дальней точки
Для набора из n точек диаграмма Вороного ( n − 1) -го порядка называется диаграммой Вороного самой дальней точки.
Для заданного набора точек S = { p 1 , p 2 , ..., p n } диаграмма Вороного для самой дальней точки делит плоскость на ячейки, в которых та же самая точка P является самой дальней точкой. Точка P имеет ячейку в диаграмме Вороного для самой дальней точки тогда и только тогда , когда она является вершиной выпуклой оболочки P . Пусть H = { h 1 , h 2 , ..., h k } будет выпуклой оболочкой P ; то диаграмма Вороного для самой дальней точки представляет собой разбиение плоскости на k ячеек, по одной для каждой точки в H , со свойством, что точка q лежит в ячейке, соответствующей узлу h i, тогда и только тогда, когда d( q , h i ) > d( q , p j ) для каждого p j ∈ S с h i ≠ p j , где d( p , q ) — евклидово расстояние между двумя точками p и q . [12] [13]
Границы ячеек в диаграмме Вороного с самой дальней точкой имеют структуру топологического дерева , с бесконечными лучами в качестве его листьев. Каждое конечное дерево изоморфно дереву, образованному таким образом из диаграммы Вороного с самой дальней точкой. [14]
Обобщения и вариации
Как следует из определения, ячейки Вороного могут быть определены для метрик, отличных от евклидовых, таких как расстояние Махаланобиса или манхэттенское расстояние . Однако в этих случаях границы ячеек Вороного могут быть более сложными, чем в евклидовом случае, поскольку равноудаленное геометрическое место для двух точек может не быть подпространством коразмерности 1, даже в двумерном случае.
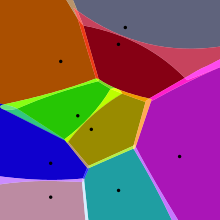
Взвешенная диаграмма Вороного — это диаграмма, в которой функция пары точек для определения ячейки Вороного является функцией расстояния, измененной мультипликативными или аддитивными весами, назначенными точкам генератора. В отличие от случая ячеек Вороного, определенных с использованием расстояния, которое является метрикой , в этом случае некоторые ячейки Вороного могут быть пустыми. Диаграмма мощности — это тип диаграммы Вороного, определяемой из набора кругов с использованием расстояния мощности ; ее также можно рассматривать как взвешенную диаграмму Вороного, в которой вес, определенный из радиуса каждого круга, добавляется к квадрату евклидова расстояния от центра круга. [15]
Диаграмма Вороного точек в -мерном пространстве может иметь вершины, требующие той же границы для объема памяти, необходимого для хранения ее явного описания. Поэтому диаграммы Вороного часто нецелесообразны для умеренных или высоких размерностей. Более эффективной с точки зрения пространства альтернативой является использование приближенных диаграмм Вороного . [16]
Диаграммы Вороного также связаны с другими геометрическими структурами, такими как срединная ось (которая нашла применение в сегментации изображений, оптическом распознавании символов и других вычислительных приложениях), прямой скелет и зонные диаграммы .
Приложения
Метеорология/Гидрология
Он используется в метеорологии и инженерной гидрологии для нахождения весов для данных об осадках станций на площади (водосборе). Точки, образующие полигоны, являются различными станциями, которые регистрируют данные об осадках. Перпендикуляры проводятся к линии, соединяющей любые две станции. Это приводит к образованию полигонов вокруг станций. Площадь, касающаяся точки станции, известна как область влияния станции. Среднее количество осадков рассчитывается по формуле
Гуманитарные и общественные науки
- В классической археологии , в частности в истории искусств , симметрия голов статуй анализируется для определения типа статуи, которой могла принадлежать отрубленная голова. Примером этого, в котором использовались ячейки Вороного, была идентификация головы Сабуроффа , которая использовала полигональную сетку высокого разрешения . [17] [18]
- В диалектометрии ячейки Вороного используются для обозначения предполагаемой языковой преемственности между точками исследования.
- В политической науке диаграммы Вороного использовались для изучения многомерной многопартийной конкуренции. [19]
Естественные науки

- В биологии диаграммы Вороного используются для моделирования ряда различных биологических структур, включая клетки [20] и микроархитектуру костей. [21] Действительно, мозаики Вороного работают как геометрический инструмент для понимания физических ограничений, которые управляют организацией биологических тканей. [22]
- В гидрологии диаграммы Вороного используются для расчета количества осадков на определенной территории на основе серии точечных измерений. В этом случае их обычно называют полигонами Тиссена.
- В экологии диаграммы Вороного используются для изучения закономерностей роста лесов и лесных пологов, а также могут быть полезны при разработке прогностических моделей лесных пожаров.
- В этологии диаграммы Вороного используются для моделирования областей опасности в теории эгоистичного стада .
- В вычислительной химии лиганд-связывающие сайты преобразуются в диаграммы Вороного для приложений машинного обучения (например, для классификации связывающих карманов в белках). [23] В других приложениях ячейки Вороного, определяемые положениями ядер в молекуле, используются для вычисления атомных зарядов . Это делается с помощью метода плотности деформации Вороного .
- В астрофизике диаграммы Вороного используются для генерации адаптивных зон сглаживания на изображениях, добавляя потоки сигнала на каждой из них. Основная цель этих процедур — поддерживать относительно постоянное отношение сигнал/шум на всех изображениях.
- В вычислительной гидродинамике мозаика Вороного набора точек может использоваться для определения вычислительных областей, используемых в методах конечных объемов , например, в космологическом коде с подвижной сеткой AREPO. [24]
- В вычислительной физике диаграммы Вороного используются для расчета профилей объекта с помощью теневой съемки и протонной радиографии в физике высокой плотности энергии . [25]
Здоровье
- В медицинской диагностике модели мышечной ткани, основанные на диаграммах Вороного, могут использоваться для выявления нервно-мышечных заболеваний. [22]
- В эпидемиологии диаграммы Вороного могут использоваться для сопоставления источников инфекций при эпидемиях. Одно из первых применений диаграмм Вороного было реализовано Джоном Сноу для изучения вспышки холеры на Брод-стрит в Сохо, Англия, в 1854 году. Он показал корреляцию между жилыми районами на карте Центрального Лондона, жители которых использовали определенный водяной насос, и районами с наибольшим количеством смертей из-за вспышки. [26]
Инженерное дело
- В физике полимеров диаграммы Вороного можно использовать для представления свободных объемов полимеров.
- В материаловедении поликристаллические микроструктуры в металлических сплавах обычно представляют с помощью мозаик Вороного.
- При росте островов диаграмма Вороного используется для оценки скорости роста отдельных островов. [27] [28] [29] [30] [31]
- В физике твердого тела ячейка Вигнера -Зейтца представляет собой мозаику Вороного твердого тела, а зона Бриллюэна представляет собой мозаику Вороного обратного ( волнового ) пространства кристаллов, имеющих симметрию пространственной группы.
- В авиации диаграммы Вороного накладываются на океанические карты для определения ближайшего аэродрома для изменения маршрута полета (см. ETOPS ) по мере выполнения самолетом своего плана полета.
- В архитектуре узоры Вороного легли в основу победившего проекта реконструкции Центра искусств Голд-Кост . [32]
- В городском планировании диаграммы Вороного могут использоваться для оценки системы зон погрузки грузов. [33]
- В горнодобывающей промышленности полигоны Вороного используются для оценки запасов ценных материалов, минералов или других ресурсов. В качестве набора точек в полигонах Вороного используются разведочные скважины.
- В поверхностной метрологии тесселяция Вороного может использоваться для моделирования шероховатости поверхности . [34]
- В робототехнике некоторые стратегии управления и алгоритмы планирования пути [35] многороботных систем основаны на разбиении среды по Вороному. [36] [37]
Математика
- Структура данных местоположения точки может быть построена поверх диаграммы Вороного для ответа на запросы ближайшего соседа , где требуется найти объект, который находится ближе всего к заданной точке запроса. Запросы ближайшего соседа имеют многочисленные приложения. Например, может потребоваться найти ближайшую больницу или наиболее похожий объект в базе данных . Большое приложение — это векторное квантование , обычно используемое при сжатии данных .
- В геометрии диаграммы Вороного можно использовать для нахождения наибольшего пустого круга среди множества точек и в охватывающем его многоугольнике; например, для строительства нового супермаркета как можно дальше от всех существующих, расположенных в определенном городе.
- Диаграммы Вороного вместе с диаграммами Вороного для самой дальней точки используются для эффективных алгоритмов вычисления округлости набора точек. [12] Подход Вороного также применяется для оценки округлости/ круглости при оценке набора данных с помощью координатно-измерительной машины .
- Нули итерированных производных рациональной функции на комплексной плоскости накапливаются на ребрах диаграммы Вороного множества полюсов (теорема Пойа-Шайреса [38] ).
Информатика
- В сетевых технологиях диаграммы Вороного можно использовать для оценки пропускной способности беспроводной сети .
- В компьютерной графике диаграммы Вороного используются для расчета 3D-геометрических моделей дробления/трещин. Они также используются для процедурной генерации органических или лавоподобных текстур.
- В автономной навигации робота диаграммы Вороного используются для поиска четких маршрутов. Если точки являются препятствиями, то края графа будут маршрутами, наиболее удаленными от препятствий (и теоретически от любых столкновений).
- В машинном обучении диаграммы Вороного используются для проведения 1-NN -классификаций. [39]
- При реконструкции глобальной сцены, в том числе с использованием случайных датчиков и нестационарного потока в кильватерном следе, геофизических данных и данных трехмерной турбулентности, мозаики Вороного используются с глубоким обучением . [40]
- При разработке пользовательского интерфейса шаблоны Вороного можно использовать для вычисления наилучшего состояния наведения для заданной точки. [41]
Алгоритмы
Известно несколько эффективных алгоритмов для построения диаграмм Вороного, как напрямую (как сама диаграмма), так и косвенно, начиная с триангуляции Делоне и затем получая ее двойственную. Прямые алгоритмы включают алгоритм Форчуна , алгоритм O ( n log( n )) для генерации диаграммы Вороного из набора точек на плоскости. Алгоритм Боуера–Уотсона , алгоритм O ( n log( n )) до O ( n 2 ) для генерации триангуляции Делоне в любом количестве измерений, может быть использован в косвенном алгоритме для диаграммы Вороного. Алгоритм Jump Flooding может генерировать приблизительные диаграммы Вороного за постоянное время и подходит для использования на обычном графическом оборудовании. [42] [43]
Алгоритм Ллойда и его обобщение с помощью алгоритма Линде–Бузо–Грея (также известного как кластеризация k-средних ) используют построение диаграмм Вороного в качестве подпрограммы. Эти методы чередуют шаги, на которых строится диаграмма Вороного для набора исходных точек, и шаги, на которых исходные точки перемещаются в новые местоположения, которые находятся ближе к центру в пределах их ячеек. Эти методы могут использоваться в пространствах произвольной размерности для итеративной сходимости к специализированной форме диаграммы Вороного, называемой центроидальной тесселяцией Вороного , где узлы перемещаются в точки, которые также являются геометрическими центрами их ячеек.
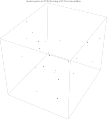
Вороной в 3D
Сетки Вороного также можно создавать в 3D.
- Случайные точки в 3D для формирования 3D разбиения Вороного
- 3D сетка Вороного из 25 случайных точек
- 3D сетка Вороного из 25 случайных точек с непрозрачностью 0,3 и точками
- 3D сетка Вороного из 25 случайных точек выпуклых многогранников
Смотрите также
Примечания
- ^ Берроу, Питер А.; Макдоннелл, Рэйчел; Макдоннелл, Рэйчел А.; Ллойд, Кристофер Д. (2015). "8.11 Ближайшие соседи: полигоны Тиссена (Дирихле/Ворони)". Принципы географических информационных систем . Oxford University Press. стр. 160–. ISBN 978-0-19-874284-5.
- ^ Лонгли, Пол А.; Гудчайлд, Майкл Ф.; Магуайр, Дэвид Дж.; Райнд, Дэвид В. (2005). "14.4.4.1 Полигоны Тиссена". Географические информационные системы и наука . Wiley. стр. 333–. ISBN 978-0-470-87001-3.
- ^ Сен, Зекай (2016). "2.8.1 Полигоны Делани, Варони и Тиссена". Принципы пространственного моделирования в науках о Земле . Springer. стр. 57–. ISBN 978-3-319-41758-5.
- ^ Ауренхаммер, Франц (1991). «Диаграммы Вороного – обзор фундаментальной геометрической структуры данных». ACM Computing Surveys . 23 (3): 345–405. doi :10.1145/116873.116880. S2CID 4613674.
- ^ Окабэ, Ацуюки; Бутс, Барри; Сугихара, Кокичи; Чиу, Сунг Нок (2000). Пространственные мозаики – концепции и приложения диаграмм Вороного (2-е изд.). John Wiley. ISBN 978-0-471-98635-5.
- ^ Бойд, Стивен; Ванденберг, Ливен (2004). Выпуклая оптимизация . Упражнение 2.9: Cambridge University Press. стр. 60.
{{cite book}}: CS1 maint: местоположение ( ссылка ) - ^ Тран, QT; Тайнар, Д.; Сафар, М. (2009). Труды по крупномасштабным системам, ориентированным на данные и знания . Springer. стр. 357. ISBN 9783642037214.
- ^ Рим 2009.
- ^ Рим 2011.
- ^ Сенечал, Марджори (1993-05-21). "Математические структуры: пространственные мозаики. Концепции и приложения диаграмм Вороного. Ацуюки Окабэ, Барри Бутс и Кокичи Сугихара. Wiley, Нью-Йорк, 1992. xii, 532 стр., илл. $89.95. Ряды Wiley по вероятности и математической статистике". Science . 260 (5111): 1170–1173. doi :10.1126/science.260.5111.1170. ISSN 0036-8075. PMID 17806355.
- ^ Вороной 1908а и Вороной 1908б.
- ^ Аб де Берг, Марк ; ван Кревелд, Марк ; Овермарс, Марк ; Шварцкопф, Отфрид (2008). Вычислительная геометрия (Третье изд.). Спрингер-Верлаг . ISBN 978-3-540-77974-2.7.4 Диаграммы Вороного для самой дальней точки. Включает описание алгоритма.
- ^ Skyum, Sven (18 февраля 1991 г.). «Простой алгоритм вычисления наименьшего охватывающего круга». Information Processing Letters . 37 (3): 121–125. doi :10.1016/0020-0190(91)90030-L., содержит простой алгоритм вычисления диаграммы Вороного для самой дальней точки.
- ^ Бидл, Тереза ; Гримм, Карстен; Палиос, Леонидас; Шевчук, Джонатан ; Вердоншот, Сандер (2016). «Реализация диаграмм Вороного для самой дальней точки». Труды 28-й Канадской конференции по вычислительной геометрии (CCCG 2016) .
- ^ Эдельсбруннер, Герберт (2012) [1987]. "13.6 Диаграммы мощности". Алгоритмы в комбинаторной геометрии . Монографии EATCS по теоретической информатике. Том 10. Springer-Verlag. С. 327–328. ISBN 9783642615689.
- ^ Сунил Арья, Сунил; Маламатос, Теохарис; Маунт, Дэвид М. (2002). «Эффективные по пространству приближенные диаграммы Вороного». Труды тридцать четвертого ежегодного симпозиума ACM по теории вычислений . стр. 721–730. doi :10.1145/509907.510011. ISBN 1581134959. S2CID 1727373.
- ^ Хёльшер, Тонио; Кремкер, Сюзанна; Мара, Юбер (2020). «Der Kopf Sabouroff в Берлине: Zwischen Archäologischer Beobachtung und Geometrischer Vermessung». Gedenkschrift für Georgios Despinis (на немецком языке). Афины, Греция: Музей Бенаки .
- ^ Voronoi Cells & Geodesic Distances - глава Sabouroff на YouTube . Анализ с использованием GigaMesh Software Framework , как описано Hölscher et al. см. doi:10.11588/heidok.00027985.
- ^ Лейвер, Майкл; Сергенти, Эрнест (2012). Партийная конкуренция: модель на основе агентов . Принстон: Princeton University Press. ISBN 978-0-691-13903-6.
- ^ Бок, Мартин; Тьяги, Амит Кумар; Крефт, Ян-Ульрих; Альт, Вольфганг (2009). «Обобщенная мозаика Вороного как модель двумерной динамики клеточной ткани». Бюллетень математической биологии . 72 (7): 1696–1731. arXiv : 0901.4469v1 . Bibcode : 2009arXiv0901.4469B. doi : 10.1007/s11538-009-9498-3. PMID 20082148. S2CID 16074264.
- ^ Хуэй Ли (2012). Баскурт, Атилла М; Ситник, Роберт (ред.). «Пространственное моделирование микроархитектуры костей». Обработка трехмерных изображений (3Dip) и приложения II . 8290 : 82900P. Bibcode : 2012SPIE.8290E..0PL. doi : 10.1117/12.907371. S2CID 1505014.
- ^ ab Санчес-Гутьеррес, Д.; Тозлуоглу, М.; Барри, Дж. Д.; Паскуаль, А.; Мао, И.; Эскудеро, Л. М. (2016-01-04). «Фундаментальные физические клеточные ограничения управляют самоорганизацией тканей». Журнал EMBO . 35 (1): 77–88. doi :10.15252/embj.201592374. PMC 4718000. PMID 26598531 .
- ^ Feinstein, Joseph; Shi, Wentao; Ramanujam, J.; Brylinski, Michal (2021). «Bionoi: представление сайтов связывания лигандов в белках на основе диаграммы Вороного для приложений машинного обучения». В Ballante, Flavio (ред.). Взаимодействие белков и лигандов и разработка лекарств. Методы в молекулярной биологии. Т. 2266. Нью-Йорк, Нью-Йорк: Springer US. стр. 299–312. doi : 10.1007/978-1-0716-1209-5_17. ISBN 978-1-0716-1209-5. PMID 33759134. S2CID 232338911 . Получено 2021-04-23 .
- ^ Springel, Volker (2010). "E pur si muove: Галилеевски-инвариантные космологические гидродинамические моделирования на движущейся сетке". MNRAS . 401 (2): 791–851. arXiv : 0901.4107 . Bibcode :2010MNRAS.401..791S. doi : 10.1111/j.1365-2966.2009.15715.x . S2CID 119241866.
- ^ Касим, Мухаммад Фирмансья (2017-01-01). «Количественная теневая фотография и протонная радиография для больших модуляций интенсивности». Physical Review E. 95 ( 2): 023306. arXiv : 1607.04179 . Bibcode : 2017PhRvE..95b3306K. doi : 10.1103/PhysRevE.95.023306. PMID 28297858. S2CID 13326345.
- ↑ Стивен Джонсон (19 октября 2006 г.). Карта призраков: история самой ужасающей эпидемии Лондона — и как она изменила науку, города и современный мир. Penguin Publishing Group. стр. 187. ISBN 978-1-101-15853-1. Получено 16 октября 2017 г.
- ^ Mulheran, PA; Blackman, JA (1996). «Зоны захвата и масштабирование при однородном росте тонкой пленки». Physical Review B. 53 ( 15): 10261–7. Bibcode : 1996PhRvB..5310261M. doi : 10.1103/PhysRevB.53.10261. PMID 9982595.
- ^ Pimpinelli, Alberto; Tumbek, Levent; Winkler, Adolf (2014). «Равенства масштабирования и экспоненты в зарождении островков: новые результаты и применение к органическим пленкам». The Journal of Physical Chemistry Letters . 5 (6): 995–8. doi :10.1021/jz500282t. PMC 3962253. PMID 24660052 .
- ^ Фанфони, М.; Плачиди, Э.; Арципрет, Ф.; Орсини, Э.; Пателла, Ф.; Бальзаротти, А. (2007). «Внезапное зарождение и масштабная инвариантность квантовых точек InAs на GaAs». Физический обзор B . 75 (24): 245312. Бибкод : 2007PhRvB..75x5312F. doi : 10.1103/PhysRevB.75.245312. ISSN 1098-0121. S2CID 120017577.
- ^ Миямото, Сатору; Мутанаббир, Усама; Халлер, Юджин Э.; Ито, Кохей М. (2009). «Пространственная корреляция самоорганизующихся изотопически чистых наноостровков Ge/Si(001)». Physical Review B. 79 ( 165415): 165415. Bibcode : 2009PhRvB..79p5415M. doi : 10.1103/PhysRevB.79.165415. ISSN 1098-0121. S2CID 13719907.
- ^ Löbl, Matthias C.; Zhai, Liang; Jahn, Jan-Philipp; Ritzmann, Julian; Huo, Yongheng; Wieck, Andreas D.; Schmidt, Oliver G.; Ludwig, Arne; Rastelli, Armando; Warburton, Richard J. (2019-10-03). "Корреляции между оптическими свойствами и площадью ячейки Вороного квантовых точек". Physical Review B. 100 ( 15): 155402. arXiv : 1902.10145 . Bibcode : 2019PhRvB.100o5402L. doi : 10.1103/physrevb.100.155402. ISSN 2469-9950. S2CID 119443529.
- ^ "GOLD COAST CULTURAL PRECINCT". Архитектура ARM. Архивировано из оригинала 2016-07-07 . Получено 2014-04-28 .
- ^ Лопес, К.; Чжао, К.-Л.; Магниоль, С.; Шиабо, Н.; Леклерк, Л. (28 февраля 2019 г.). «Микроскопическое моделирование движения при парковке грузовиков как мера управления зоной погрузки грузов». Устойчивость . 11 (5), 1276.
- ^ Сингх, К.; Садеги, Ф.; Корренс, М.; Бласс, Т. (декабрь 2019 г.). «Подход на основе микроструктуры к моделированию эффектов шероховатости поверхности на усталость при растяжении». Международный журнал усталости . 129 : 105229. doi : 10.1016/j.ijfatigue.2019.105229. S2CID 202213370.
- ^ Niu, Hanlin; Savvaris, Al; Tsourdos, Antonios; Ji, Ze (2019). «Алгоритм планирования пути на основе карты видимости Вороного для беспилотных наземных транспортных средств» (PDF) . The Journal of Navigation . 72 (4): 850–874. doi :10.1017/S0373463318001005. S2CID 67908628.
- ^ Кортес, Дж.; Мартинес, С.; Каратас, Т.; Булло, Ф. (апрель 2004 г.). «Управление покрытием для мобильных сенсорных сетей». Труды IEEE по робототехнике и автоматизации . 20 (2): 243–255. doi :10.1109/TRA.2004.824698. ISSN 2374-958X. S2CID 2022860.
- ^ Теруэль, Энрике; Арагуэс, Росарио; Лопес-Николас, Гонсало (апрель 2021 г.). «Практический метод равномерного покрытия динамической области роем». IEEE Robotics and Automation Letters . 6 (2): 1359–1366. doi :10.1109/LRA.2021.3057568. ISSN 2377-3766. S2CID 232071627.
- ^ Полиа, Г. О нулях производных функции и их аналитическом характере. Бюллетень АМН, том 49, выпуск 3, 178-191, 1943.
- ^ Митчелл, Том М. (1997). Машинное обучение (Международное издание). McGraw-Hill. стр. 233. ISBN 978-0-07-042807-2.
- ^ Шенвай, Танушри (18.11.2021). «Новая технология глубокого обучения, которая перестраивает глобальные поля без использования организованных данных датчиков». MarkTechPost . Получено 05.12.2021 .
- ↑ Архивировано в Ghostarchive и Wayback Machine: «Марк ДиМарко: алгоритмы пользовательского интерфейса [JSConf2014]». 11 июня 2014 г. – через www.youtube.com.
- ^ Ронг, Годонг; Тан, Тиов Сенг (2006). "Jump flooding in GPU with applications to Voronoi diagram and distance transform" (PDF) . В Олано, Марк; Секин, Карло Х. (ред.). Труды симпозиума 2006 года по интерактивной 3D-графике, SI3D 2006, 14-17 марта 2006 г., Редвуд-Сити, Калифорния, США . ACM. стр. 109–116. doi :10.1145/1111411.1111431. ISBN 1-59593-295-X.
- ^ "Шейдертой".
Ссылки
- Ауренхаммер, Франц ; Кляйн, Рольф; Ли, Дер-Цай (2013). Диаграммы Вороного и триангуляции Делоне . World Scientific. ISBN 978-9814447638.
- Боуер, Адриан (1981). «Вычисление мозаик Дирихле». Comput. J. 24 (2): 162–166. doi : 10.1093/comjnl/24.2.162 .
- де Берг, Марк; ван Кревелд, Марк; Овермарс, Марк ; Шварцкопф, Отфрид (2000). «7. Диаграммы Вороного». Вычислительная геометрия (2-е исправленное изд.). Спрингер. стр. 47–163. ISBN 978-3-540-65620-3. Включает описание алгоритма Fortune.
- Кляйн, Рольф (1988). «Абстрактные диаграммы Вороного и их приложения: расширенные абстрактные». Вычислительная геометрия и ее приложения . Конспект лекций по информатике . Том 333. Springer. С. 148–157. doi :10.1007/3-540-50335-8_31. ISBN 978-3-540-52055-9.
- Лежен Дирихле, Ж. (1850). «Über die Reduktion der Positive Squaretischen Formen mit Drei unbestimmten ganzen Zahlen». Журнал для королевы и математики . 1850 (40): 209–227. дои : 10.1515/crll.1850.40.209. S2CID 199546675.
- Окабе, Ацуюки; Бутс, Барри; Сугихара, Кокичи ; Чиу, Сунг Нок (2000). Пространственные мозаики — концепции и применение диаграмм Вороного (2-е изд.). Wiley. ISBN 0-471-98635-6.
- Reem, Daniel (2009). "Алгоритм вычисления диаграмм Вороного общих генераторов в общих нормированных пространствах". Труды Шестого международного симпозиума по диаграммам Вороного в науке и технике (ISVD 2009) . стр. 144–152. doi :10.1109/ISVD.2009.23. ISBN 978-1-4244-4769-5.
- Рим, Дэниел (2011). «Геометрическая устойчивость диаграмм Вороного относительно малых изменений узлов». Труды двадцать седьмого ежегодного симпозиума по вычислительной геометрии . С. 254–263. arXiv : 1103.4125 . Bibcode :2011arXiv1103.4125R. doi :10.1145/1998196.1998234. ISBN 9781450306829. S2CID 14639512.
- Тиссен, Альфред Х. (июль 1911 г.). «Средние значения осадков для больших территорий». Monthly Weather Review . 39 (7). Американское метеорологическое общество: 1082–1089. Bibcode : 1911MWRv...39R1082T. doi : 10.1175/1520-0493(1911)39<1082b:pafla>2.0.co;2 .
- Вороной, Жорж (1908а). «Новые приложения непрерывных параметров в теории квадратичных форм. Premier mémoire. Sur quelques proprietés des formes положительные парфаиты» (PDF) . Журнал для королевы и математики . 1908 (133): 97–178. дои : 10.1515/crll.1908.133.97. S2CID 116775758.
- Вороной, Жорж (1908b). «Новые приложения непрерывных параметров в теории квадратных форм. Deuxième mémoire. Recherches sur les parallélloèdres primitifs» (PDF) . Журнал для королевы и математики . 1908 (134): 198–287. дои : 10.1515/crll.1908.134.198. S2CID 118441072.
- Уотсон, Дэвид Ф. (1981). «Вычисление n-мерной мозаики Делоне с применением к многогранникам Вороного». Comput. J. 24 (2): 167–172. doi : 10.1093/comjnl/24.2.167 .
Внешние ссылки
- Вайсштейн, Эрик В. «Диаграмма Вороного». Математический мир .
- Диаграммы Вороного в CGAL , библиотеке алгоритмов вычислительной геометрии
- Демонстрационная программа для алгоритма SFTessellation, которая создает диаграмму Вороного с использованием модели степного пожара



























![{\displaystyle \ell _{2}=d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]={\sqrt {\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dbecd722552090b30fcd0166107f3a2cece7e8d)
![{\displaystyle d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9da43d1f11cfcb755e4600f943fe4c8dedd46263)