Вычислительная химия

Вычислительная химия — это раздел химии , который использует компьютерное моделирование для решения химических задач. [2] Она использует методы теоретической химии, встроенные в компьютерные программы, для расчета структур и свойств молекул , групп молекул и твердых тел. [3] Важность этого предмета проистекает из того факта, что, за исключением некоторых относительно недавних открытий, связанных с молекулярным ионом водорода ( дигидрогенным катионом ), достижение точного квантово-механического описания химических систем аналитически или в замкнутой форме не представляется возможным. [4] Сложность, присущая проблеме многих тел, усугубляет проблему предоставления подробных описаний квантово-механических систем. [5] Хотя результаты вычислений обычно дополняют информацию, полученную в ходе химических экспериментов , они иногда могут предсказывать ненаблюдаемые химические явления . [6]
Обзор
Вычислительная химия отличается от теоретической химии , которая включает математическое описание химии. Однако вычислительная химия включает использование компьютерных программ и дополнительных математических навыков для точного моделирования различных химических проблем. В теоретической химии химики, физики и математики разрабатывают алгоритмы и компьютерные программы для прогнозирования атомных и молекулярных свойств и путей химических реакций. Вычислительные химики, напротив, могут просто применять существующие компьютерные программы и методологии к конкретным химическим вопросам. [7]
Исторически вычислительная химия имела два различных аспекта:
- Вычислительные исследования, используемые для поиска отправной точки для лабораторного синтеза или для помощи в понимании экспериментальных данных, таких как положение и источник спектроскопических пиков. [8]
- Вычислительные исследования, используемые для прогнозирования возможности существования до сих пор совершенно неизвестных молекул или для исследования механизмов реакций, которые нелегко изучить с помощью экспериментов. [8]
Эти аспекты, наряду с целью вычислительной химии, привели к появлению целого ряда алгоритмов.
История
Основываясь на основополагающих открытиях и теориях в истории квантовой механики , первые теоретические расчеты в химии были сделаны Уолтером Гайтлером и Фритцем Лондоном в 1927 году с использованием теории валентных связей . [9] Книги, оказавшие влияние на раннее развитие вычислительной квантовой химии, включают « Введение в квантовую механику – с приложениями к химии» Лайнуса Полинга и Э. Брайта Уилсона 1935 года , [10] «Квантовая химия» Айринга , Уолтера и Кимбалла 1944 года , [11] «Элементарная волновая механика – с приложениями к квантовой химии» Гайтлера 1945 года , [12] и позднее учебник Коулсона 1952 года «Валентность» , каждая из которых служила основным источником информации для химиков в последующие десятилетия. [13]
С развитием эффективной компьютерной технологии в 1940-х годах решения сложных волновых уравнений для сложных атомных систем стали достижимой целью. В начале 1950-х годов были выполнены первые полуэмпирические расчеты атомных орбиталей. Теоретические химики стали активными пользователями первых цифровых компьютеров. Одно из значительных достижений было отмечено статьей Клеменса К. Дж. Рутана 1951 года в Reviews of Modern Physics. [14] [15] Эта статья в основном была сосредоточена на подходе «LCAO MO» (линейная комбинация атомных орбиталей молекулярных орбиталей). В течение многих лет она была второй по частоте цитирования статьей в этом журнале. [14] [15] Очень подробный отчет о таком использовании в Соединенном Королевстве дан Смитом и Сатклиффом. [16] Первые ab initio расчеты по методу Хартри-Фока для двухатомных молекул были выполнены в 1956 году в Массачусетском технологическом институте с использованием базисного набора орбиталей Слейтера . [17] Для двухатомных молекул систематическое исследование с использованием минимального базисного набора и первый расчет с большим базисным набором были опубликованы Рансилом и Несбетом соответственно в 1960 году. [18] Первые полиатомные расчеты с использованием гауссовых орбиталей были выполнены в конце 1950-х годов. Первые расчеты конфигурационного взаимодействия были выполнены в Кембридже на компьютере EDSAC в 1950-х годах с использованием гауссовых орбиталей Бойзом и его коллегами. [19] К 1971 году, когда была опубликована библиография ab initio расчетов, [20] самыми большими включенными молекулами были нафталин и азулен . [21] [22] Рефераты многих более ранних разработок в области ab initio теории были опубликованы Шефером. [23]
В 1964 году на компьютерах в Беркли и Оксфорде были проведены расчеты по методу Хюккеля (с использованием метода простой линейной комбинации атомных орбиталей (ЛКАО) для определения электронных энергий молекулярных орбиталей π-электронов в сопряженных углеводородных системах) молекул, начиная от бутадиена и бензола и заканчивая оваленом . [24] Эти эмпирические методы были заменены в 1960-х годах полуэмпирическими методами, такими как CNDO . [25]
В начале 1970-х годов эффективные компьютерные программы ab initio, такие как ATMOL, Gaussian , IBMOL и POLYAYTOM, начали использоваться для ускорения ab initio расчетов молекулярных орбиталей. [26] Из этих четырех программ только Gaussian, теперь значительно расширенная, все еще используется, но сейчас используются и многие другие программы. [26] В то же время были разработаны методы молекулярной механики , такие как силовое поле MM2 , в первую очередь Норманом Аллингером . [27]
Одно из первых упоминаний термина «вычислительная химия» можно найти в книге 1970 года « Компьютеры и их роль в физических науках» Сиднея Фернбаха и Абрахама Хаскелла Тауба, где они утверждают: «Поэтому кажется, что «вычислительная химия» может наконец стать все более и более реальностью». [28] В 1970-х годах самые разные методы стали рассматриваться как часть новой зарождающейся дисциплины вычислительной химии . [29] Журнал «Вычислительная химия» был впервые опубликован в 1980 году.
Вычислительная химия была отмечена несколькими Нобелевскими премиями, наиболее заметными из которых были премии 1998 и 2013 годов. Вальтер Кон , «за разработку теории функционала плотности», и Джон Попл , «за разработку вычислительных методов в квантовой химии», получили Нобелевскую премию по химии 1998 года. [30] Мартин Карплус , Майкл Левитт и Арье Варшел получили Нобелевскую премию по химии 2013 года за «разработку многомасштабных моделей для сложных химических систем». [31]
Приложения
В вычислительной химии существует несколько направлений.
- Предсказание молекулярной структуры молекул с использованием моделирования сил или более точных квантово-химических методов для нахождения стационарных точек на энергетической поверхности при изменении положения ядер. [32]
- Хранение и поиск данных о химических объектах (см. химические базы данных ). [33]
- Выявление корреляций между химическими структурами и свойствами (см. количественную связь структура-свойство (QSPR) и количественную связь структура-активность (QSAR)). [34]
- Вычислительные подходы, помогающие эффективно синтезировать соединения. [35]
- Вычислительные подходы к проектированию молекул, которые взаимодействуют определенным образом с другими молекулами (например, проектирование лекарств и катализ ). [36]
Эти поля могут иметь несколько применений, как показано ниже.
Катализ

Вычислительная химия — это инструмент для анализа каталитических систем без проведения экспериментов. Современная электронная теория структуры и теория функционала плотности позволили исследователям обнаружить и понять катализаторы . [37] Вычислительные исследования применяют теоретическую химию к исследованию катализа. Методы теории функционала плотности вычисляют энергии и орбитали молекул, чтобы получить модели этих структур. [38] Используя эти методы, исследователи могут предсказывать такие значения, как энергия активации , реакционная способность сайта [39] и другие термодинамические свойства. [38]
Данные, которые трудно получить экспериментально, можно найти, используя вычислительные методы для моделирования механизмов каталитических циклов. [39] Опытные вычислительные химики дают прогнозы, близкие к экспериментальным данным с надлежащим учетом методов и базисных наборов. С хорошими вычислительными данными исследователи могут предсказать, как можно улучшить катализаторы, чтобы снизить стоимость и повысить эффективность этих реакций. [38]
Разработка лекарств
Вычислительная химия используется в разработке лекарств для моделирования потенциально полезных молекул лекарств и помогает компаниям экономить время и деньги при разработке лекарств. Процесс открытия лекарств включает анализ данных, поиск способов улучшения текущих молекул, поиск синтетических путей и тестирование этих молекул. [36] Вычислительная химия помогает в этом процессе, давая прогнозы о том, какие эксперименты лучше всего провести, не проводя другие эксперименты. Вычислительные методы также могут находить значения, которые трудно найти экспериментально, такие как pKa соединений. [40] Такие методы, как теория функционала плотности, могут использоваться для моделирования молекул лекарств и нахождения их свойств, таких как их энергии HOMO и LUMO и молекулярные орбитали. Вычислительные химики также помогают компаниям в разработке информатики, инфраструктуры и дизайна лекарств. [41]
Помимо синтеза лекарств, носители лекарств также исследуются вычислительными химиками для наноматериалов . Это позволяет исследователям моделировать среды для проверки эффективности и стабильности носителей лекарств. Понимание того, как вода взаимодействует с этими наноматериалами, обеспечивает стабильность материала в организме человека. Эти вычислительные симуляции помогают исследователям оптимизировать материал, найти лучший способ структурировать эти наноматериалы перед их изготовлением. [42]
Базы данных вычислительной химии
Базы данных полезны как для вычислительных, так и для невычислительных химиков в исследованиях и проверке достоверности вычислительных методов. Эмпирические данные используются для анализа погрешности вычислительных методов по сравнению с экспериментальными данными. Эмпирические данные помогают исследователям с их методами и базисными наборами иметь большую уверенность в результатах исследователей. Базы данных вычислительной химии также используются при тестировании программного обеспечения или оборудования для вычислительной химии. [43]
Базы данных также могут использовать чисто расчетные данные. Чисто расчетные данные используют расчетные значения вместо экспериментальных значений для баз данных. Чисто расчетные данные избегают работы с этими корректировками для различных экспериментальных условий, таких как энергия нулевой точки. Эти расчеты также могут избежать экспериментальных ошибок для сложных для тестирования молекул. Хотя чисто расчетные данные часто не идеальны, выявление проблем часто проще для расчетных данных, чем для экспериментальных. [43]
Базы данных также предоставляют публичный доступ к информации для использования исследователями. Они содержат данные, которые другие исследователи нашли и загрузили в эти базы данных, чтобы любой мог их искать. Исследователи используют эти базы данных, чтобы найти информацию о молекулах, представляющих интерес, и узнать, что можно сделать с этими молекулами. Некоторые общедоступные химические базы данных включают следующее. [43]
- BindingDB : Содержит экспериментальную информацию о взаимодействиях белков и малых молекул. [44]
- RCSB : хранит общедоступные 3D-модели макромолекул (белков, нуклеиновых кислот) и малых молекул (лекарств, ингибиторов) [45]
- ChEMBL : Содержит данные исследований по разработке лекарственных препаратов, такие как результаты анализов. [43]
- DrugBank : данные о механизмах действия лекарств можно найти здесь. [43]
Методы
Ab initioметод
Программы, используемые в вычислительной химии, основаны на многих различных квантово-химических методах, которые решают молекулярное уравнение Шредингера, связанное с молекулярным гамильтонианом . [46] Методы, которые не включают никаких эмпирических или полуэмпирических параметров в свои уравнения, будучи выведенными непосредственно из теории, без включения экспериментальных данных, называются методами ab initio . [47] Теоретическое приближение строго определяется на первых принципах, а затем решается в пределах погрешности, которая качественно известна заранее. Если необходимо использовать численные итерационные методы, цель состоит в том, чтобы повторять до тех пор, пока не будет получена полная машинная точность (наилучшее, что возможно при конечной длине слова на компьютере и в пределах сделанных математических и/или физических приближений). [48]
Методы ab initio должны определять уровень теории (метод) и базисный набор. [49] Базисный набор состоит из функций, центрированных на атомах молекулы. Затем эти наборы используются для описания молекулярных орбиталей с помощью линейной комбинации атомных орбиталей (LCAO) молекулярный орбитальный метод ansatz . [50]
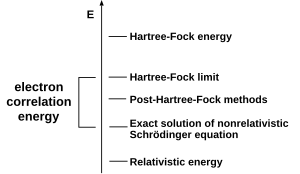
Распространенным типом расчета электронной структуры ab initio является метод Хартри-Фока (HF), расширение теории молекулярных орбиталей , где отталкивание электронов в молекуле специально не учитывается; в расчет включается только средний эффект электронов. По мере увеличения размера базисного набора энергия и волновая функция стремятся к пределу, называемому пределом Хартри-Фока. [50]
Многие типы вычислений начинаются с вычисления Хартри-Фока и впоследствии корректируются для электрон-электронного отталкивания, называемого также электронной корреляцией . [51] Эти типы вычислений называются пост-Хартри-Фоковскими методами. Постоянно совершенствуя эти методы, ученые могут все больше приближаться к идеальному предсказанию поведения атомных и молекулярных систем в рамках квантовой механики, как определено уравнением Шредингера. [52] Чтобы получить точное согласие с экспериментом, необходимо включить определенные термины, некоторые из которых гораздо важнее для тяжелых атомов, чем для легких. [53]
В большинстве случаев волновая функция Хартри-Фока занимает одну конфигурацию или определитель. [54] В некоторых случаях, особенно для процессов разрыва связей, этого недостаточно, и необходимо использовать несколько конфигураций . [55]
Полная молекулярная энергия может быть оценена как функция молекулярной геометрии ; другими словами, поверхность потенциальной энергии . [56] Такая поверхность может быть использована для динамики реакции. Стационарные точки поверхности приводят к предсказаниям различных изомеров и переходных структур для конверсии между изомерами, но их можно определить без полного знания полной поверхности. [53]

Вычислительная термохимия
Особенно важной задачей, называемой вычислительной термохимией , является расчет термохимических величин, таких как энтальпия образования, с химической точностью. Химическая точность — это точность, необходимая для создания реалистичных химических прогнозов, и обычно считается равной 1 ккал/моль или 4 кДж/моль. Чтобы достичь этой точности экономичным способом, необходимо использовать ряд методов пост-Хартри–Фока и объединить результаты. Эти методы называются композитными методами квантовой химии . [57]
Химическая динамика
После разделения электронных и ядерных переменных в представлении Борна-Оппенгеймера) волновой пакет, соответствующий ядерным степеням свободы, распространяется посредством оператора эволюции времени (физики), связанного с зависящим от времени уравнением Шредингера (для полного молекулярного гамильтониана ). [58] В подходе, зависящем от дополнительной энергии, независимое от времени уравнение Шредингера решается с использованием формализма теории рассеяния . Потенциал, представляющий межатомное взаимодействие, задается поверхностями потенциальной энергии . В общем случае поверхности потенциальной энергии связаны посредством членов вибронной связи . [59]
Наиболее популярными методами распространения волнового пакета , связанными с молекулярной геометрией, являются:
- полином Чебышева (действительный) , [60]
- многоконфигурационный метод Хартри, зависящий от времени (MCTDH), [61]
- полуклассический метод
- и метод оператора разделения, описанный ниже. [62]
Техника разделения операторов
То, как вычислительный метод решает квантовые уравнения, влияет на точность и эффективность метода. Метод разделения операторов является одним из таких методов решения дифференциальных уравнений. В вычислительной химии метод разделения операторов снижает вычислительные затраты на моделирование химических систем. Вычислительные затраты — это то, сколько времени требуется компьютерам для расчета этих химических систем, поскольку для более сложных систем это может занять несколько дней. Квантовые системы сложны и требуют много времени для решения людьми. Методы разделения операторов помогают компьютерам быстро рассчитывать эти системы, решая подзадачи в квантовом дифференциальном уравнении . Метод делает это путем разделения дифференциального уравнения на два разных уравнения, например, когда имеется более двух операторов. После решения разделенные уравнения снова объединяются в одно уравнение, чтобы дать легко вычисляемое решение. [62]
Этот метод используется во многих областях, где требуется решение дифференциальных уравнений, например, в биологии . Однако, этот метод сопровождается ошибкой расщепления. Например, со следующим решением для дифференциального уравнения. [62]
Уравнение можно разделить, но решения не будут точными, только похожими. Это пример расщепления первого порядка. [62]
Существуют способы уменьшить эту ошибку, в том числе взять среднее значение двух разделенных уравнений. [62]
Другой способ повышения точности — использовать расщепление более высокого порядка. Обычно расщепление второго порядка — это самое большее, что делается, потому что расщепление более высокого порядка требует гораздо больше времени для расчета и не стоит затрат. Методы более высокого порядка становятся слишком сложными для реализации и бесполезны для решения дифференциальных уравнений, несмотря на более высокую точность. [62]
Химики-вычислители тратят много времени на то, чтобы сделать системы, рассчитанные с помощью техники оператора разделения, более точными, минимизируя при этом вычислительные затраты. Методы расчета представляют собой сложную задачу для многих химиков, пытающихся моделировать молекулы или химические среды. [62]

Методы функционала плотности
Методы теории функционала плотности (DFT) часто считаются методами ab initio для определения молекулярной электронной структуры, хотя многие из наиболее распространенных функционалов используют параметры, полученные из эмпирических данных или из более сложных вычислений. В DFT полная энергия выражается в терминах полной одноэлектронной плотности, а не волновой функции. В этом типе вычислений есть приближенный гамильтониан и приближенное выражение для полной электронной плотности. Методы DFT могут быть очень точными при небольших вычислительных затратах. Некоторые методы объединяют функционал обмена функционала плотности с обменным членом Хартри-Фока и называются гибридными функциональными методами. [63]
Полуэмпирические методы
Полуэмпирические методы квантовой химии основаны на формализме метода Хартри-Фока , но делают много приближений и получают некоторые параметры из эмпирических данных. Они были очень важны в вычислительной химии с 60-х по 90-е годы, особенно для обработки больших молекул, где полный метод Хартри-Фока без приближений был слишком затратным. Использование эмпирических параметров, по-видимому, позволяет включить в методы некоторое количество эффектов корреляции. [64]
Примитивные полуэмпирические методы были разработаны еще раньше, где двухэлектронная часть гамильтониана явно не включена. Для π-электронных систем это был метод Хюккеля , предложенный Эрихом Хюккелем , а для всех валентных электронных систем — расширенный метод Хюккеля , предложенный Роальдом Хоффманном . Иногда методы Хюккеля называют «полностью эмпирическими», поскольку они не выводятся из гамильтониана. [65] Тем не менее, термин «эмпирические методы» или «эмпирические силовые поля» обычно используется для описания молекулярной механики. [66]

Молекулярная механика
Во многих случаях большие молекулярные системы можно успешно моделировать, полностью избегая квантово-механических расчетов. Например, молекулярно-механические симуляции используют одно классическое выражение для энергии соединения, например, гармонический осциллятор . Все константы, появляющиеся в уравнениях, должны быть получены заранее из экспериментальных данных или расчетов ab initio . [64]
База данных соединений, используемых для параметризации, т. е. результирующий набор параметров и функций называется силовым полем , имеет решающее значение для успеха расчетов молекулярной механики. Силовое поле, параметризованное против определенного класса молекул, например, белков, как ожидается, будет иметь какое-либо значение только при описании других молекул того же класса. [64] Эти методы могут быть применены к белкам и другим крупным биологическим молекулам и позволяют изучать подход и взаимодействие (стыковку) потенциальных молекул лекарств. [67] [68]
Молекулярная динамика
Молекулярная динамика (МД) использует либо квантовую механику , либо молекулярную механику , либо их смесь для расчета сил, которые затем используются для решения законов движения Ньютона для изучения поведения систем, зависящего от времени. Результатом моделирования молекулярной динамики является траектория, которая описывает, как положение и скорость частиц изменяются со временем. Фазовая точка системы, описываемая положениями и импульсами всех ее частиц в предыдущей точке времени, определит следующую фазовую точку во времени путем интегрирования по законам движения Ньютона. [69]
Монте-Карло
Монте-Карло (МК) генерирует конфигурации системы, внося случайные изменения в положения ее частиц, вместе с их ориентацией и конформацией, где это уместно. [70] Это метод случайной выборки, который использует так называемую выборку по важности . Методы выборки по важности способны генерировать состояния с низкой энергией, поскольку это позволяет точно рассчитывать свойства. Потенциальная энергия каждой конфигурации системы может быть рассчитана вместе со значениями других свойств из положений атомов. [71] [72]
Квантовая механика/молекулярная механика (КМ/ММ)
QM/MM — это гибридный метод, который пытается объединить точность квантовой механики со скоростью молекулярной механики. Он полезен для моделирования очень больших молекул, таких как ферменты . [73]
Квантовая вычислительная химия
Квантовая вычислительная химия нацелена на использование квантовых вычислений для моделирования химических систем, отличаясь от подхода QM/MM (квантовая механика/молекулярная механика). [74] В то время как QM/MM использует гибридный подход, объединяя квантовую механику для части системы с классической механикой для остальной части, квантовая вычислительная химия использует исключительно квантовые методы вычислений для представления и обработки информации, такие как гамильтоновы операторы. [75]
Обычные методы вычислительной химии часто сталкиваются со сложными квантово-механическими уравнениями, особенно из-за экспоненциального роста волновой функции квантовой системы. Квантовая вычислительная химия решает эти проблемы, используя квантовые вычислительные методы , такие как кубитизация и квантовая фазовая оценка , которые, как считается, предлагают масштабируемые решения. [76]
Квантовая фазовая оценка, с другой стороны, помогает точно определить собственные энергетические состояния, которые имеют решающее значение для понимания поведения квантовой системы. [77]
Хотя эти методы продвинули область вычислительной химии, особенно в моделировании химических систем, их практическое применение в настоящее время ограничено в основном более мелкими системами из-за технологических ограничений. Тем не менее, эти разработки могут привести к значительному прогрессу в достижении более точных и ресурсоэффективных симуляций квантовой химии. [76]
Вычислительные затраты в химических алгоритмах
Вычислительная стоимость и алгоритмическая сложность в химии используются для понимания и прогнозирования химических явлений. Они помогают определить, какие алгоритмы/вычислительные методы использовать при решении химических проблем. В этом разделе основное внимание уделяется масштабированию вычислительной сложности в зависимости от размера молекулы и подробно описываются алгоритмы, обычно используемые в обеих областях. [78]
В квантовой химии, в частности, сложность может расти экспоненциально с числом электронов, вовлеченных в систему. Этот экспоненциальный рост является существенным препятствием для точного моделирования больших или сложных систем. [79]
Продвинутые алгоритмы в обеих областях стремятся сбалансировать точность с вычислительной эффективностью. Например, в МД такие методы, как интеграция Верле или алгоритм Бимана, используются для их вычислительной эффективности. В квантовой химии гибридные методы, объединяющие различные вычислительные подходы (например, КМ/ММ), все чаще используются для решения больших биомолекулярных систем. [80]
Примеры алгоритмической сложности
Следующий список иллюстрирует влияние вычислительной сложности на алгоритмы, используемые в химических вычислениях. Важно отметить, что хотя этот список и содержит ключевые примеры, он не является исчерпывающим и служит лишь руководством для понимания того, как вычислительные требования влияют на выбор конкретных вычислительных методов в химии.
Молекулярная динамика
Алгоритм
Решает уравнения движения Ньютона для атомов и молекул. [81]
Сложность
Стандартный расчет парного взаимодействия в МД приводит к сложности для частиц. Это происходит потому, что каждая частица взаимодействует с каждой другой частицей, что приводит к взаимодействиям. [82] Продвинутые алгоритмы, такие как суммирование Эвальда или быстрый мультипольный метод, сводят это к или даже группируют отдаленные частицы и рассматривают их как единое целое или используют умные математические аппроксимации. [83] [84]
Квантовая механика/молекулярная механика (КМ/ММ)
Алгоритм
Объединяет квантово-механические расчеты для небольшой области с молекулярной механикой для более крупной среды. [85]
Сложность
Сложность методов QM/MM зависит как от размера квантовой области, так и от метода, используемого для квантовых вычислений. Например, если для квантовой части используется метод Хартри-Фока, сложность может быть аппроксимирована как , где — число базисных функций в квантовой области. Эта сложность возникает из-за необходимости решать набор связанных уравнений итеративно до тех пор, пока не будет достигнута самосогласованность. [86]
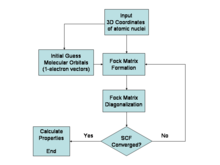
Метод Хартри-Фока
Алгоритм
Находит единственное состояние Фока, которое минимизирует энергию. [87]
Сложность
NP-трудный или NP-полный, как показано путем встраивания примеров модели Изинга в вычисления Хартри-Фока. Метод Хартри-Фока включает решение уравнений Рутана-Холла, которые масштабируются в зависимости от реализации, причем является числом базисных функций. Вычислительные затраты в основном связаны с оценкой и преобразованием двухэлектронных интегралов. Это доказательство NP-трудности или NP-полноты происходит от встраивания таких проблем, как модель Изинга, в формализм Хартри-Фока. [87]
Теория функционала плотности
Алгоритм
Исследует электронную структуру или ядерную структуру многочастичных систем, таких как атомы, молекулы и конденсированные фазы . [89]
Сложность
Традиционные реализации DFT обычно масштабируются как , в основном из-за необходимости диагонализации матрицы Кона-Шэма . [90] Шаг диагонализации, который находит собственные значения и собственные векторы матрицы, вносит наибольший вклад в это масштабирование. Последние достижения в DFT направлены на уменьшение этой сложности с помощью различных приближений и алгоритмических улучшений. [91]
Стандартный метод CCSD и CCSD(T)
Алгоритм
Методы CCSD и CCSD(T) представляют собой передовые методы электронной структуры, включающие одиночные, двойные и, в случае CCSD(T), тройные пертурбативные возбуждения для расчета эффектов электронной корреляции. [92]
Сложность
CCSD
Масштабируется как , где - число базисных функций. Эта интенсивная вычислительная потребность возникает из-за включения одиночных и двойных возбуждений в расчет электронной корреляции. [92]
ККСД(Т)
С добавлением пертурбативных троек сложность увеличивается до . Эта повышенная сложность ограничивает практическое использование более мелкими системами, обычно до 20-25 атомов в обычных реализациях. [92]

Метод линейного масштабирования CCSD(T)
Алгоритм
Адаптация стандартного метода CCSD(T) с использованием локальных естественных орбиталей (NO) для значительного снижения вычислительной нагрузки и возможности применения в более крупных системах. [92]
Сложность
Достигает линейного масштабирования с размером системы, что является значительным улучшением по сравнению с традиционным масштабированием пятой степени CCSD. Это достижение позволяет применять практические приложения к молекулам до 100 атомов с разумными базисными наборами, что является значительным шагом вперед в способности вычислительной химии обрабатывать более крупные системы с высокой точностью. [92]
Доказательство классов сложности для алгоритмов включает комбинацию математического доказательства и вычислительных экспериментов. Например, в случае метода Хартри-Фока доказательство NP-трудности является теоретическим результатом, полученным из теории сложности, в частности, посредством редукций из известных NP-трудных задач. [93]
Для других методов, таких как MD или DFT, вычислительная сложность часто наблюдается эмпирически и поддерживается анализом алгоритма. В этих случаях доказательство корректности в меньшей степени касается формальных математических доказательств, а в большей — последовательного наблюдения за вычислительным поведением в различных системах и реализациях. [93]
Точность
Вычислительная химия не является точным описанием реальной химии, поскольку математические и физические модели природы могут дать только приближение. Однако большинство химических явлений можно описать в определенной степени в качественной или приблизительной количественной вычислительной схеме. [94]
Молекулы состоят из ядер и электронов, поэтому применяются методы квантовой механики . Химики-вычислители часто пытаются решить нерелятивистское уравнение Шредингера с добавлением релятивистских поправок, хотя некоторый прогресс был достигнут в решении полностью релятивистского уравнения Дирака . В принципе, можно решить уравнение Шредингера либо в его зависящей от времени, либо в независимой от времени форме, в зависимости от решаемой задачи; на практике это невозможно, за исключением очень малых систем. Поэтому большое количество приближенных методов стремятся достичь наилучшего компромисса между точностью и вычислительными затратами. [95]
Точность всегда можно улучшить за счет больших вычислительных затрат. Значительные ошибки могут возникнуть в моделях ab initio , включающих много электронов, из-за вычислительных затрат полных релятивистских инклюзивных методов. [92] Это усложняет изучение молекул, взаимодействующих с атомами с высокой атомной массой, такими как переходные металлы и их каталитические свойства. Современные алгоритмы в вычислительной химии могут в обычном режиме рассчитывать свойства малых молекул, которые содержат до 40 электронов с ошибками для энергий менее нескольких кДж/моль. Для геометрий длины связей могут быть предсказаны в пределах нескольких пикометров, а углы связей в пределах 0,5 градуса. Обработка более крупных молекул, которые содержат несколько десятков атомов, вычислительно поддается более приближенным методам, таким как теория функционала плотности (DFT). [96]
В этой области ведутся споры о том, достаточны ли последние методы для описания сложных химических реакций, например, в биохимии. Большие молекулы можно изучать полуэмпирическими приближенными методами. Еще более крупные молекулы обрабатываются методами классической механики , которые используют то, что называется молекулярной механикой (ММ). В методах КМ-ММ небольшие части больших комплексов обрабатываются квантово-механически (КМ), а остальная часть обрабатывается приближенно (ММ). [97]
Пакеты программного обеспечения
Существует множество самодостаточных пакетов программного обеспечения для вычислительной химии . Некоторые включают множество методов, охватывающих широкий диапазон, в то время как другие концентрируются на очень узком диапазоне или даже на одном методе. Подробную информацию о большинстве из них можно найти в:
- Программы биомолекулярного моделирования: белки , нуклеиновые кислоты .
- Программы по молекулярной механике .
- Программное обеспечение для квантовой химии и физики твердого тела, поддерживающее несколько методов.
- Программное обеспечение для молекулярного дизайна
- Полуэмпирические программы.
- Программы валентных связей .
Специализированные журналы по вычислительной химии
- Ежегодные отчеты по вычислительной химии
- Вычислительная и теоретическая химия
- Вычислительная и теоретическая полимерная наука
- Компьютеры и химическая инженерия
- Журнал химической информации и моделирования
- Журнал химического программного обеспечения
- Журнал химической теории и вычислений
- Журнал хемоинформатики
- Журнал вычислительной химии
- Журнал компьютерной химии
- Журнал компьютерной химии Япония
- Журнал компьютерного молекулярного дизайна
- Журнал теоретической и вычислительной химии
- Молекулярная информатика
- Теоретические химические отчеты
Внешние ссылки
- База данных NIST Computational Chemistry Comparison and Benchmark DataBase – содержит базу данных тысяч результатов вычислений и экспериментов для сотен систем.
- Отделение компьютеров в химии Американского химического общества – Отделение компьютеров в химии Американского химического общества, ресурсы для грантов, наград, контактов и встреч.
- Отчет CSTB Математические исследования в материаловедении: возможности и перспективы – Отчет CSTB
- 3.320 Атомистическое компьютерное моделирование материалов (SMA 5107) Бесплатный курс MIT
- Chem 4021/8021 Вычислительная химия Бесплатный курс Университета Миннесоты
- Технологическая дорожная карта для вычислительной химии
- Приложения молекулярного и материального моделирования.
- Влияние достижений в области вычислительных и коммуникационных технологий на химическую науку и технологию Отчет CSTB
- Приложения MD и вычислительной химии на графических процессорах
- Susi Lehtola, Antti J. Karttunen: «Свободное и открытое программное обеспечение для обучения вычислительной химии», Впервые опубликовано: 23 марта 2022 г., https://doi.org/10.1002/wcms.1610 (Открытый доступ) Архивировано 9 августа 2022 г. на Wayback Machine
- CCL.NET: Computational Chemistry List, Ltd.
Смотрите также
- Список специалистов по вычислительной химии
- Биоинформатика
- Вычислительная биология
- Список вычислительной химии
- Эффективная генерация кода с помощью компьютерной алгебры
- Сравнение реализаций силового поля
- Важные публикации по вычислительной химии
- В силико
- Международная академия квантово-молекулярной науки
- Математическая химия
- Молекулярная графика
- Молекулярное моделирование
- Молекулярное моделирование на графических процессорах
- Молекулярное моделирование Монте-Карло
- Молекулярная динамика Кар-Парринелло
- Динамика белка
- Научные вычисления
- Статистическая механика
- Модели растворителей
Ссылки
- ^ "WebMO". www.webmo.net . Получено 2023-12-05 .
- ^ Parrill, Abby L.; Lipkowitz, Kenny B., ред. (19.10.2018). Обзоры вычислительной химии, том 31. Том 4 (1-е изд.). Wiley. doi :10.1002/series6143. ISBN 978-1-119-51802-0.
- ^ Комитет Национального исследовательского совета (США) по проблемам химических наук в 21 веке (2003), «Химическая теория и компьютерное моделирование: от вычислительной химии к инженерии технологических систем», Beyond the Molecular Frontier: Challenges for Chemistry and Chemical Engineering , National Academies Press (США) , дата обращения 2023-12-05
- ^ Коробов, Владимир И.; Карр, Ж.-Ф. (2021-09-07). "Вибрационные спин-усредненные переходы в молекулярных ионах водорода". Physical Review A. 104 ( 3): 032806. arXiv : 2107.14497 . Bibcode : 2021PhRvA.104c2806K. doi : 10.1103/PhysRevA.104.032806. S2CID 236635049.
- ^ Nozières, Philippe (1997). Теория взаимодействующих систем Ферми . Расширенная классика книг. Кембридж, Массачусетс: Perseus Publishing. ISBN 978-0-201-32824-0.
- ^ Виллемс, Генриетта; Де Сеско, Стефан; Свенссон, Фредрик (24.09.2020). «Вычислительная химия на бюджете: поддержка открытия лекарств при ограниченных ресурсах: миниперспектива». Журнал медицинской химии . 63 (18): 10158–10169. doi : 10.1021/acs.jmedchem.9b02126. ISSN 0022-2623. PMID 32298123. S2CID 215802432.
- ^ Крамер, Кристофер Дж. (2014). Основы вычислительной химии: теории и модели . Чичестер: Wiley. ISBN 978-0-470-09182-1.
- ^ ab Patel, Prajay; Melin, Timothé RL; North, Sasha C.; Wilson, Angela K. (01.01.2021), Dixon, David A. (ред.), «Глава четвертая — Методологии ab initio composite: их значение для химического сообщества», Annual Reports in Computational Chemistry , т. 17, Elsevier, стр. 113–161, doi : 10.1016/bs.arcc.2021.09.002, S2CID 244017999 , получено 03.12.2023
- ^ Хайтлер, В.; Лондон, Ф. (1 июня 1927 г.). «Wechselwirkung Neutraler Atome und homopolare Bindung nach der Quantenmechanik». Zeitschrift für Physik (на немецком языке). 44 (6): 455–472. Бибкод : 1927ZPhy...44..455H. дои : 10.1007/BF01397394. ISSN 0044-3328. S2CID 119739102.
- ^ Полинг, Линус ; Уилсон, Эдгар Брайт (1985). Введение в квантовую механику: с приложениями к химии . Нью-Йорк: Dover Publications. ISBN 978-0-486-64871-2.
- ^ Айринг, Генри ; Уолтер, Джон; Кимбалл, Джордж Э. (1967). Квантовая химия (14-е печатное издание). Нью-Йорк: Wiley. ISBN 978-0-471-24981-8.
- ^ Гейтлер, В. (1956-01-01). Элементарная волновая механика с приложениями к квантовой химии (2-е изд.). Oxford University Press. ISBN 978-0-19-851103-8.
- ^ Коулсон, Чарльз Альфред ; МакВини, Рой (1991). Валентность Коулсона . Oxford science publications (3-е изд.). Оксфорд Нью-Йорк Торонто [и т.д.]: Oxford university press. ISBN 978-0-19-855145-4.
- ^ ab Roothaan, CCJ (1951-04-01). "Новые разработки в теории молекулярных орбиталей". Reviews of Modern Physics . 23 (2): 69–89. Bibcode : 1951RvMP...23...69R. doi : 10.1103/RevModPhys.23.69.
- ^ ab Ruedenberg, Klaus (1954-11-01). "Модель сети свободных электронов для сопряженных систем. V. Энергии и распределения электронов в модели FE MO и в модели LCAO MO". Журнал химической физики . 22 (11): 1878–1894. Bibcode : 1954JChPh..22.1878R. doi : 10.1063/1.1739935. ISSN 0021-9606.
- ^ Смит, С. Дж.; Сатклифф, Б. Т. (1997). «Развитие вычислительной химии в Соединенном Королевстве». Обзоры в области вычислительной химии . 10 : 271–316.
- ^ Boys, SF; Cook, GB; Reeves, CM; Shavitt, I. (1956-12-01) [1 декабря 1956]. "Автоматические фундаментальные расчеты молекулярной структуры". Nature . 178 (4544): 1207–1209. Bibcode :1956Natur.178.1207B. doi :10.1038/1781207a0. ISSN 1476-4687. S2CID 4218995.
- ^ Шефер, Генри Ф. III (1972). Электронная структура атомов и молекул . Рединг, Массачусетс: Addison-Wesley Publishing Co. стр. 146.
- ^ Boys, SF ; Cook, GB; Reeves, CM; Shavitt, I. (1956). "Автоматические фундаментальные расчеты молекулярной структуры". Nature . 178 (2): 1207. Bibcode : 1956Natur.178.1207B. doi : 10.1038/1781207a0. S2CID 4218995.
- ^ Ричардс, WG; Уокер, TEH; Хинкли RK (1971). Библиография ab initio молекулярных волновых функций . Оксфорд: Clarendon Press.
- ^ Пройсс, Х. (1968). «DasSCF-MO-P(LCGO)-Verfahren und seine Varianten». Международный журнал квантовой химии . 2 (5): 651. Бибкод : 1968IJQC....2..651P. дои : 10.1002/qua.560020506.
- ^ Бюнкер, Р. Дж.; Пейеримхофф, С. Д. (1969). «Расчеты SCF ab initio для азулена и нафталина». Chemical Physics Letters . 3 (1): 37. Bibcode : 1969CPL.....3...37B. doi : 10.1016/0009-2614(69)80014-X.
- ^ Шефер, Генри Ф. III (1984). Квантовая химия . Оксфорд: Clarendon Press.
- ^ Streitwieser, A.; Brauman, JI; Coulson, CA (1965). Дополнительные таблицы расчетов молекулярных орбиталей . Oxford: Pergamon Press.
- ^ Попл, Джон А .; Беверидж, Дэвид Л. (1970). Приближенная теория молекулярных орбиталей . Нью-Йорк: McGraw Hill.
- ^ ab Ma, Xiaoyue (2022-12-01). "Развитие вычислительной химии и применение вычислительных методов". Journal of Physics: Conference Series . 2386 (1): 012005. Bibcode : 2022JPhCS2386a2005M. doi : 10.1088/1742-6596/2386/1/012005 . ISSN 1742-6588.
- ^ Аллингер, Норман (1977). «Конформационный анализ. 130. ММ2. Силовое поле углеводородов, использующее торсионные члены V1 и V2». Журнал Американского химического общества . 99 (25): 8127–8134. doi :10.1021/ja00467a001.
- ^ Фернбах, Сидней; Тауб, Авраам Хаскелл (1970). Компьютеры и их роль в физических науках . Routledge. ISBN 978-0-677-14030-8.
- ^ Кенни Б. Липковиц; Дональд Б. Бойд, ред. (1990). "том 1, предисловие". Обзоры по вычислительной химии . Том 1. Wiley. doi :10.1002/9780470125786. ISBN 978-0-470-12578-6.
- ^ «Нобелевская премия по химии 1998 года».
- ^ "Нобелевская премия по химии 2013 года" (пресс-релиз). Королевская шведская академия наук. 9 октября 2013 г. Получено 9 октября 2013 г.
- ^ Musil, Felix; Grisafi, Andrea; Bartók, Albert P.; Ortner, Christoph; Csányi, Gábor; Ceriotti, Michele (2021-08-25). «Структурные представления молекул и материалов, вдохновленные физикой». Chemical Reviews . 121 (16): 9759–9815. arXiv : 2101.04673 . doi : 10.1021/acs.chemrev.1c00021 . ISSN 0009-2665. PMID 34310133.
- ^ Муресан, Сорель; Сицманн, Маркус; Саутан, Кристофер (2012), Ларсон, Ричард С. (ред.), «Сопоставление баз данных соединений и белковых мишеней», Биоинформатика и открытие лекарств , Методы в молекулярной биологии, т. 910, Тотова, Нью-Джерси: Humana Press, стр. 145–164, doi : 10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-965-5, PMC 7449375 , PMID 22821596 , получено 2023-12-03
- ^ Рой, Кунал; Кар, Супратик; Дас, Рудра Нараян (2015). Понимание основ QSAR для приложений в фармацевтических науках и оценке рисков . Амстердам Бостон: Elsevier/Academic Press. ISBN 978-0-12-801505-6.
- ^ Фэн, Фань; Лай, Лухуа; Пэй, Цзяньфэн (2018). «Вычислительный анализ химического синтеза и проектирование путей». Frontiers in Chemistry . 6 : 199. doi : 10.3389/fchem.2018.00199 . ISSN 2296-2646. PMC 5994992. PMID 29915783 .
- ^ ab Tsui, Vickie; Ortwine, Daniel F.; Blaney, Jeffrey M. (2017-03-01). «Возможность принятия решений по проектам открытия лекарств с помощью интегрированной вычислительной химии и информатики». Журнал компьютерного молекулярного дизайна . 31 (3): 287–291. Bibcode : 2017JCAMD..31..287T. doi : 10.1007/s10822-016-9988-y. ISSN 1573-4951. PMID 27796615. S2CID 23373414.
- ^ Elnabawy, Ahmed O.; Rangarajan, Srinivas; Mavrikakis, Manos (2015-08-01). «Вычислительная химия для синтеза NH3, гидроочистки и восстановления NOx: три темы, представляющие особый интерес для Haldor Topsøe». Журнал катализа . Специальный выпуск: Влияние Haldor Topsøe на катализ. 328 : 26–35. doi :10.1016/j.jcat.2014.12.018. ISSN 0021-9517.
- ^ abc Patel, Prajay; Wilson, Angela K. (2020-12-01). «Соображения вычислительной химии в катализе: региоселективность и диссоциация металл-лиганд». Catalysis Today . Труды 3-й Международной конференции по катализу и химической инженерии. 358 : 422–429. doi : 10.1016/j.cattod.2020.07.057 . ISSN 0920-5861. S2CID 225472601.
- ^ ab van Santen, RA (1996-05-06). "Computational-chemical achievement in heterogeneous catalysis". Journal of Molecular Catalysis A: Chemical . Труды 8-го Международного симпозиума по связям между гомогенным и гетерогенным катализом. 107 (1): 5–12. doi :10.1016/1381-1169(95)00161-1. ISSN 1381-1169. S2CID 59580128.
- ^ ван Влиймен, Герман; Дежарле, Рене Л.; Мирзадеган, Тара (март 2017 г.). «Вычислительная химия в Janssen». Журнал компьютерного молекулярного дизайна . 31 (3): 267–273. Bibcode : 2017JCAMD..31..267V. doi : 10.1007/s10822-016-9998-9. ISSN 1573-4951. PMID 27995515. S2CID 207166545.
- ^ Ахмад, Имад; Кузнецов, Алексей Э.; Пирзада, Абдул Сабур; Альшариф, Халаф Ф.; Даглиа, Мария; Хан, Харун (2023). «Вычислительная фармакология и вычислительная химия 4-гидроксиизолейцина: физико-химические, фармакокинетические и основанные на DFT подходы». Frontiers in Chemistry . 11. Bibcode : 2023FrCh...1145974A. doi : 10.3389/fchem.2023.1145974 . ISSN 2296-2646. PMC 10133580. PMID 37123881 .
- ^ Эль-Магид, Х. Р. Абд; Мустафа, Ф. М.; Абдель-Латиф, Махмуд К. (2022-01-02). «Нанокластеры, наночастицы и нанотрубки нитрида бора как носитель лекарственного средства для противотуберкулезного препарата изониазид, подходы вычислительной химии». Журнал биомолекулярной структуры и динамики . 40 (1): 226–235. doi :10.1080/07391102.2020.1814871. ISSN 0739-1102. PMID 32870128. S2CID 221403943.
- ^ abcde Муресан, Сорель; Сицманн, Маркус; Саутан, Кристофер (2012), Ларсон, Ричард С. (ред.), «Сопоставление баз данных соединений и белковых мишеней», Биоинформатика и открытие лекарств , Методы в молекулярной биологии, т. 910, Тотова, Нью-Джерси: Humana Press, стр. 145–164, doi : 10.1007/978-1-61779-965-5_8, ISBN 978-1-61779-964-8, PMC 7449375 , PMID 22821596
- ^ Gilson, Michael K.; Liu, Tiqing; Baitaluk, Michael; Nicola, George; Hwang, Linda; Chong, Jenny (2016-01-04). "BindingDB в 2015 году: публичная база данных для медицинской химии, вычислительной химии и системной фармакологии". Nucleic Acids Research . 44 (D1): D1045–1053. doi :10.1093/nar/gkv1072. ISSN 1362-4962. PMC 4702793. PMID 26481362 .
- ^ Зардеки, Кристин; Дутта, Шучисмита; Гудселл, Дэвид С.; Фойгт, Мария; Берли, Стивен К. (2016-03-08). «Банк данных белков RCSB: Ресурс для химических, биохимических и структурных исследований больших и малых биомолекул». Журнал химического образования . 93 (3): 569–575. Bibcode : 2016JChEd..93..569Z. doi : 10.1021/acs.jchemed.5b00404 . ISSN 0021-9584.
- ^ "Вычислительная химия и молекулярное моделирование". SpringerLink . 2008. doi :10.1007/978-3-540-77304-7. ISBN 978-3-540-77302-3. S2CID 102140015.
- ^ Лич, Эндрю Р. (2009). Молекулярное моделирование: принципы и приложения (2-е изд., 12-е изд. [Доктора]). Harlow: Pearson/Prentice Hall. ISBN 978-0-582-38210-7.
- ^ Сюй, Пэн; Вестхаймер, Брайс М.; Шлинсог, Меган; Саттасатучана, Тосапорн; Эллиотт, Джордж; Гордон, Марк С.; Гидез, Эмили (2024-01-01). "Эффективный фрагментный потенциал: силовое поле Ab Initio". Comprehensive Computational Chemistry : 153–161. doi :10.1016/B978-0-12-821978-2.00141-0. ISBN 978-0-12-823256-9.
- ^ Фризнер, Ричард А. (2005-05-10). «Ab initio квантовая химия: Методология и приложения». Труды Национальной академии наук . 102 (19): 6648–6653. doi : 10.1073/pnas.0408036102 . ISSN 0027-8424. PMC 1100737. PMID 15870212 .
- ^ ab Hinchliffe, Alan (2001). Моделирование молекулярных структур . Серия Wiley по теоретической химии (2-е, переиздание). Чичестер: Wiley. ISBN 978-0-471-48993-1.
- ^ S, DR Hartree FR (1947-01-01). "Расчет атомных структур". Reports on Progress in Physics . 11 (1): 113–143. Bibcode :1947RPPh...11..113S. doi :10.1088/0034-4885/11/1/305. S2CID 250826906.
- ^ Møller, Chr.; Plesset, MS (1934-10-01). «Заметка о приближенном подходе к многоэлектронным системам». Physical Review . 46 (7): 618–622. Bibcode :1934PhRv...46..618M. doi :10.1103/PhysRev.46.618. ISSN 0031-899X.
- ^ ab Матвеева, Регина; Фолкестад, Сарай Дери; Хёйвик, Ида-Мари (2023-02-09). «Теория Хартри–Фока, разрушающая частицы, для открытых молекулярных систем». Журнал физической химии A . 127 (5). Американское химическое общество: 1329–1341. Bibcode :2023JPCA..127.1329M. doi :10.1021/acs.jpca.2c07686. ISSN 1089-5639. PMC 9923758 . PMID 36720055.
- ^ Маклахлан, А.Д.; Болл, М.А. (1964-07-01). "Теория Хартри-Фока, зависящая от времени, для молекул". Обзоры современной физики . 36 (3): 844–855. Bibcode : 1964RvMP...36..844M. doi : 10.1103/RevModPhys.36.844.
- ^ Коэн, Морис; Келли, Пол С. (1967-05-01). "ВОЛНОВЫЕ ФУНКЦИИ ХАРТРИ–ФОКА ДЛЯ ВОЗБУЖДЕННЫХ СОСТОЯНИЙ: III. ДИПОЛЬНЫЕ ПЕРЕХОДЫ В ТРЕХЭЛЕКТРОННЫХ СИСТЕМАХ". Canadian Journal of Physics . 45 (5): 1661–1673. Bibcode :1967CaJPh..45.1661C. doi :10.1139/p67-129. ISSN 0008-4204.
- ^ Баллард, Эндрю Дж.; Дас, Ританкар; Мартиниани, Стефано; Мехта, Дхагаш; Сагун, Левент; Стивенсон, Джейкоб Д.; Уэйлс, Дэвид Дж. (2017-05-24). «Энергетические ландшафты для машинного обучения». Физическая химия Химическая физика . 19 (20): 12585–12603. arXiv : 1703.07915 . Bibcode :2017PCCP...1912585B. doi :10.1039/C7CP01108C. ISSN 1463-9084. PMID 28367548.
- ^ Олингер, WS; Клунзингер, PE; Деппмайер, BJ; Хере, WJ (2009-03-12). «Эффективный расчет теплот образования». Журнал физической химии A. 113 ( 10): 2165–2175. doi :10.1021/jp810144q. ISSN 1089-5639. PMID 19222177.
- ^ Батлер, Лори Дж. (октябрь 1998 г.). «Динамика химических реакций за пределами приближения Борна-Оппенгеймера». Annual Review of Physical Chemistry . 49 (1): 125–171. Bibcode : 1998ARPC...49..125B. doi : 10.1146/annurev.physchem.49.1.125. ISSN 0066-426X. PMID 15012427.
- ^ Ито, Кенити; Накамура, Шу (июнь 2010 г.). «Теория рассеяния, зависящая от времени, для операторов Шредингера на рассеивающих многообразиях». Журнал Лондонского математического общества . 81 (3): 774–792. arXiv : 0810.1575 . doi : 10.1112/jlms/jdq018. S2CID 8115409.
- ^ Эмброуз, Д.; Каунселл, Дж. Ф.; Дэвенпорт, А. Дж. (1970-03-01). «Использование полиномов Чебышева для представления давлений пара между тройной точкой и критической точкой». Журнал химической термодинамики . 2 (2): 283–294. Bibcode : 1970JChTh...2..283A. doi : 10.1016/0021-9614(70)90093-5. ISSN 0021-9614.
- ^ Manthe, U.; Meyer, H.-D.; Cederbaum, LS (1992-09-01). "Динамика волновых пакетов в рамках многоконфигурационной модели Хартри: общие аспекты и применение к NOCl". Журнал химической физики . 97 (5): 3199–3213. Bibcode : 1992JChPh..97.3199M. doi : 10.1063/1.463007. ISSN 0021-9606.
- ^ abcdefg Lukassen, Axel Ariaan; Kiehl, Martin (2018-12-15). «Операторное расщепление для систем химических реакций с быстрой химией». Журнал вычислительной и прикладной математики . 344 : 495–511. doi : 10.1016/j.cam.2018.06.001 . ISSN 0377-0427. S2CID 49612142.
- ^ Де Профт, Франк; Гирлингс, Пол; Гейдар-Заде, Фарназ; Айерс, Пол В. (2024-01-01). «Концептуальная теория функционала плотности». Comprehensive Computational Chemistry : 306–321. doi :10.1016/B978-0-12-821978-2.00025-8. ISBN 978-0-12-823256-9.
- ^ abc Рамачандран, КИ; Дипа, Г.; Намбури, К. (2008). Вычислительная химия и молекулярное моделирование: принципы и приложения . Берлин: Springer. ISBN 978-3-540-77304-7.
- ^ Counts, Richard W. (1987-07-01). "Стратегии I". Журнал компьютерного молекулярного дизайна . 1 (2): 177–178. Bibcode : 1987JCAMD...1..177C. doi : 10.1007/bf01676961. ISSN 0920-654X. PMID 3504968. S2CID 40429116.
- ^ Динур, Ури; Хаглер, Арнольд Т. (1991). Липковиц, Кенни Б.; Бойд, Дональд Б. (ред.). Обзоры по вычислительной химии . John Wiley & Sons, Inc., стр. 99–164. дои : 10.1002/9780470125793.ch4. ISBN 978-0-470-12579-3.
- ^ Рубенштейн, Лестер А.; Заухар, Рэнди Дж.; Ланзара, Ричард Г. (2006). «Молекулярная динамика биофизической модели активации β2-адренергических и G-белковых рецепторов» (PDF) . Журнал молекулярной графики и моделирования . 25 (4): 396–409. doi :10.1016/j.jmgm.2006.02.008. PMID 16574446. Архивировано (PDF) из оригинала 27.02.2008.
- ^ Рубенштейн, Лестер А.; Ланзара, Ричард Г. (1998). «Активация рецепторов, сопряженных с G-белком, влечет за собой цистеиновую модуляцию связывания агониста» (PDF) . Журнал молекулярной структуры: THEOCHEM . 430 : 57–71. doi :10.1016/S0166-1280(98)90217-2. Архивировано (PDF) из оригинала 2004-05-30.
- ^ Хуттер, Юрг; Ианнуцци, Марселла; Кюне, Томас Д. (2024-01-01). «Ab Initio Молекулярная динамика: Руководство по приложениям». Comprehensive Computational Chemistry : 493–517. doi :10.1016/B978-0-12-821978-2.00096-9. ISBN 978-0-12-823256-9.
- ^ Satoh, A. (2003-01-01), Satoh, A. (ред.), "Глава 3 - Методы Монте-Карло", Исследования в области науки о интерфейсах , Введение в молекулярно-микромоделирование коллоидных дисперсий, т. 17, Elsevier, стр. 19–63, doi :10.1016/S1383-7303(03)80031-5, ISBN 978-0-444-51424-0, получено 2023-12-03
- ^ Аллен, MP (1987). Компьютерное моделирование жидкостей . DJ Tildesley. Оксфорд [Англия]: Clarendon Press. ISBN 0-19-855375-7. OCLC 15132676.
- ^ Макардл, Сэм; Эндо, Сугуру; Аспуру-Гузик, Алан; Бенджамин, Саймон К.; Юань, Сяо (2020-03-30). «Квантовая вычислительная химия». Reviews of Modern Physics . 92 (1): 015003. arXiv : 1808.10402 . Bibcode : 2020RvMP...92a5003M. doi : 10.1103/RevModPhys.92.015003 . ISSN 0034-6861.
- ^ Биньон, Эммануэль; Монари, Антонио (2024-01-01). «Молекулярная динамика и квантовая механика/микроскопия для понимания организации и воспроизводства генома у появляющихся РНК-вирусов». Comprehensive Computational Chemistry : 895–909. doi :10.1016/B978-0-12-821978-2.00101-X. ISBN 978-0-12-823256-9. S2CID 258397837.
- ^ Абрамс, Дэниел С.; Ллойд, Сет (1999-12-13). «Квантовый алгоритм, обеспечивающий экспоненциальное увеличение скорости поиска собственных значений и собственных векторов». Physical Review Letters . 83 (24): 5162–5165. arXiv : quant-ph/9807070 . Bibcode : 1999PhRvL..83.5162A. doi : 10.1103/PhysRevLett.83.5162. S2CID 118937256.
- ^ Фейнман, Ричард П. (2019-06-17). Эй, Тони; Аллен, Робин В. (ред.). Лекции Фейнмана по вычислениям. Бока-Ратон: CRC Press. doi :10.1201/9780429500442. ISBN 978-0-429-50044-2. S2CID 53898623.
- ^ ab Nielsen, Michael A.; Chuang, Isaac L. (2010). Квантовые вычисления и квантовая информация (10-я годовщина издания). Кембридж: Cambridge university press. ISBN 978-1-107-00217-3.
- ^ Макардл, Сэм; Эндо, Сугуру; Аспуру-Гузик, Алан; Бенджамин, Саймон К.; Юань, Сяо (30.03.2020). «Квантовая вычислительная химия». Reviews of Modern Physics . 92 (1): 015003. arXiv : 1808.10402 . Bibcode : 2020RvMP...92a5003M. doi : 10.1103/RevModPhys.92.015003 .
- ^ Jäger, Jonas; Krems, Roman V. (2023-02-02). «Универсальная выразительность вариационных квантовых классификаторов и квантовых ядер для опорных векторных машин». Nature Communications . 14 (1). Nature: 576. arXiv : 2207.05865 . Bibcode :2023NatCo..14..576J. doi :10.1038/s41467-023-36144-5. ISSN 2041-1723. PMC 9895068 . PMID 36732519.
- ^ Современная электронная теория структуры. 1. Расширенная серия по физической химии. Сингапур: World Scientific. 1995. ISBN 978-981-02-2987-0.
- ^ Эдкок, Стюарт А.; Маккаммон, Дж. Эндрю (2006-05-01). «Молекулярная динамика: обзор методов моделирования активности белков». Chemical Reviews . 106 (5): 1589–1615. doi :10.1021/cr040426m. ISSN 0009-2665. PMC 2547409 . PMID 16683746.
- ^ Дюррант, Джейкоб Д.; Маккаммон, Дж. Эндрю (28.10.2011). «Моделирование молекулярной динамики и открытие лекарств». BMC Biology . 9 (1): 71. doi : 10.1186/1741-7007-9-71 . ISSN 1741-7007. PMC 3203851. PMID 22035460 .
- ^ Стефан, Саймон; Хорш, Мартин Т.; Врабец, Ядран; Хассе, Ханс (2019-07-03). «MolMod – база данных силовых полей с открытым доступом для молекулярного моделирования жидкостей». Молекулярное моделирование . 45 (10): 806–814. arXiv : 1904.05206 . doi : 10.1080/08927022.2019.1601191. ISSN 0892-7022. S2CID 119199372.
- ^ Курзак, Дж.; Петтит, Б.М. (сентябрь 2006 г.). «Быстрые мультипольные методы для динамики частиц». Молекулярное моделирование . 32 (10–11): 775–790. doi :10.1080/08927020600991161. ISSN 0892-7022. PMC 2634295. PMID 19194526 .
- ^ Гизе, Тимоти Дж.; Пантева, Мария Т.; Чен, Хаоюань; Йорк, Даррин М. (2015-02-10). «Многополярные методы Эвальда, 1: Теория, точность и производительность». Журнал химической теории и вычислений . 11 (2): 436–450. doi :10.1021/ct5007983. ISSN 1549-9618. PMC 4325605. PMID 25691829 .
- ^ Гроенхоф, Геррит (2013), Монтичелли, Лука; Салонен, Эмппу (ред.), «Введение в QM/MM-симуляции», Биомолекулярные симуляции: методы и протоколы , Методы в молекулярной биологии, т. 924, Тотова, Нью-Джерси: Humana Press, стр. 43–66, doi : 10.1007/978-1-62703-017-5_3, hdl : 11858/00-001M-0000-0010-15DF-C , ISBN 978-1-62703-017-5, PMID 23034745
- ^ Tzeliou, Christina Eleftheria; Mermigki, Markella Aliki; Tzeli, Demeter (январь 2022 г.). «Обзор методологий QM/MM и их применение к металлопротеинам». Molecules . 27 (9): 2660. doi : 10.3390/molecules27092660 . ISSN 1420-3049. PMC 9105939 . PMID 35566011.
- ^ ab Лукас, Эндрю (2014). "Изинговские формулировки многих NP-задач". Frontiers in Physics . 2 : 5. arXiv : 1302.5843 . Bibcode : 2014FrP.....2....5L. doi : 10.3389/fphy.2014.00005 . ISSN 2296-424X.
- ^ Растегар, Сомайех Ф.; Хадипур, Нассер Л.; Табар, Мохаммад Бигдели; Солейманабади, Хамед (2013-09-01). "Исследования DFT адсорбции молекул акролеина на чистых и легированных Al графенах". Журнал молекулярного моделирования . 19 (9): 3733–3740. doi :10.1007/s00894-013-1898-5. ISSN 1610-2940. PMID 23793719. S2CID 41375235.
- ^ Kohn, W.; Sham, LJ (1965-11-15). "Самосогласованные уравнения, включающие эффекты обмена и корреляции". Physical Review . 140 (4A): A1133–A1138. Bibcode :1965PhRv..140.1133K. doi : 10.1103/PhysRev.140.A1133 .
- ^ Мишо-Риу, Винсент; Чжан, Лэй; Го, Хун (2016-02-15). «RESCU: Метод электронной структуры реального пространства». Журнал вычислительной физики . 307 : 593–613. arXiv : 1509.05746 . Bibcode : 2016JCoPh.307..593M. doi : 10.1016/j.jcp.2015.12.014. ISSN 0021-9991. S2CID 28836129.
- ^ Мотамарри, Фани; Дас, Самбит; Рудрараджу, Шива; Гош, Кришненду; Давыдов, Денис; Гавини, Викрам (01 января 2020 г.). «DFT-FE - массово-параллельный адаптивный код конечных элементов для крупномасштабных расчетов по теории функционала плотности». Компьютерная физика. Коммуникации . 246 : 106853. arXiv : 1903.10959 . Бибкод : 2020CoPhC.24606853M. дои : 10.1016/j.cpc.2019.07.016. ISSN 0010-4655. S2CID 85517990.
- ^ abcdef Сенгупта, Аркаджоти; Рамабхадран, Рагхунат О.; Рагхавачари, Кришнан (2016-01-15). «Преодоление узкого места: точная экстраполяция к «золотому стандарту» энергий CCSD(T) для больших органических радикалов с открытой оболочкой при сниженных вычислительных затратах». Журнал вычислительной химии . 37 (2): 286–295. doi :10.1002/jcc.24050. ISSN 0192-8651. PMID 26280676. S2CID 23011794.
- ^ ab Whitfield, James Daniel; Love, Peter John; Aspuru-Guzik, Alán (2013). «Вычислительная сложность в электронной структуре». Phys. Chem. Chem. Phys . 15 (2): 397–411. arXiv : 1208.3334 . Bibcode :2013PCCP...15..397W. doi :10.1039/C2CP42695A. ISSN 1463-9076. PMID 23172634. S2CID 12351374.
- ^ Математические проблемы теоретической/вычислительной химии. Вашингтон, округ Колумбия: National Academies Press. 1995-03-29. doi :10.17226/4886. ISBN 978-0-309-05097-5.
- ^ Вишер, Лукас (июнь 2002 г.). «Уравнение Дирака в квантовой химии: стратегии преодоления текущих вычислительных проблем». Журнал вычислительной химии . 23 (8): 759–766. doi :10.1002/jcc.10036. ISSN 0192-8651. PMID 12012352. S2CID 19427995.
- ^ Сакс, Александр Ф. (2008-04-01). «Методы вычислительной химии: охватывающие порядки величин в пространстве, времени и точности». Monatshefte für Chemie - Chemical Monthly . 139 (4): 299–308. doi :10.1007/s00706-007-0827-7. ISSN 1434-4475. S2CID 85451980.
- ^ Friesner, R. (2003-03-01). «Как железосодержащие белки контролируют химию дикислорода: подробное описание на атомном уровне с помощью точных квантово-химических и смешанных квантово-механических/молекулярно-механических расчетов». Coordination Chemistry Reviews . 238–239: 267–290. doi :10.1016/S0010-8545(02)00284-9. ISSN 0010-8545.













