Перетаскивание (физика)

В гидродинамике сопротивление , иногда называемое сопротивлением жидкости , представляет собой силу , действующую противоположно относительному движению любого объекта, движущегося по отношению к окружающей жидкости . ^[1] Это может существовать между двумя слоями жидкости, двумя твердыми поверхностями или между жидкостью и твердой поверхностью. Силы сопротивления имеют тенденцию уменьшать скорость жидкости относительно твердого объекта на пути жидкости.

В отличие от других сил сопротивления, сила сопротивления зависит от скорости. ^{[2] [3]} Сила сопротивления пропорциональна относительной скорости для низкоскоростного потока и пропорциональна квадрату скорости для высокоскоростного потока. Это различие между низкоскоростным и высокоскоростным потоком измеряется числом Рейнольдса .

Примеры сопротивления включают в себя:

• Чистая аэродинамическая или гидродинамическая сила : сопротивление, действующее в направлении, противоположном направлению движения твердого объекта, например, автомобиля, самолета ^[3] и корпуса лодок.
• Вязкое сопротивление жидкости в трубе : сила сопротивления неподвижной трубе ограничивает скорость жидкости в трубе. ^{[4] [5]}
• В физике спорта сила сопротивления необходима для объяснения движения мячей, копий, стрел и фрисби, а также производительности бегунов и пловцов. ^[6] Для лучшего спринтера преодоление сопротивления может потребовать 5% от его выходной энергии. ^[7]

Существует много различных типов сопротивления, вызванных различными физическими взаимодействиями между объектом и жидкостью. Два типа сопротивления актуальны для всех объектов:

• Сопротивление формы , которое вызвано давлением, оказываемым на объект, когда поток жидкости обтекает объект. Сопротивление формы определяется формой поперечного сечения и площадью тела.
• Сопротивление трения поверхности (или вязкостное сопротивление), которое вызвано трением между жидкостью и поверхностью объекта. Поверхность может быть внешней частью объекта, например, корпусом лодки, или внутренней частью объекта, например, отверстием трубы.

Существует два типа, которые в первую очередь актуальны для самолетов:

• Сопротивление, вызванное подъемной силой, возникает у крыльев или несущего корпуса в авиации, а также у полуглиссирующих или глиссирующих корпусов водных транспортных средств.
• Волновое сопротивление ( аэродинамика ) вызвано наличием ударных волн и впервые появляется на дозвуковых скоростях самолета, когда локальные скорости потока становятся сверхзвуковыми. Волновое сопротивление сверхзвукового прототипа самолета Concorde было уменьшено на скорости Маха 2 на 1,8% путем применения правила площади , которое удлинило заднюю часть фюзеляжа на 3,73 м (12,2 фута) на серийном самолете. ^[8]

Волновое сопротивление влияет на плавсредство:

• Волновое сопротивление (гидродинамика судна) возникает, когда твердый объект движется вдоль границы жидкости и создает поверхностные волны .

Наконец, в аэродинамике часто используется термин «паразитное сопротивление». Паразитное сопротивление представляет собой сумму сопротивления формы и сопротивления трения обшивки и является полностью отрицательным для самолета, в отличие от сопротивления, вызванного подъемной силой, которое является следствием создания подъемной силы.

Форма и течение	Форма перетаскивания	Трение кожи
	≈0%	≈100%
	≈10%	≈90%
	≈90%	≈10%
	≈100%	≈0%

Влияние обтекаемости на относительные пропорции трения поверхности и сопротивления формы показано в таблице справа для аэродинамического профиля, который является обтекаемым телом, и цилиндра, который является плохо обтекаемым телом. Также показана плоская пластина в двух различных ориентациях, иллюстрирующая влияние ориентации на относительные пропорции трения поверхности и сопротивления формы, а также показывающая разницу давления между передней и задней частями.

Тело известно как тупое или обтекаемое, когда источником сопротивления являются силы давления, и обтекаемое, если сопротивлением являются силы вязкости. Например, дорожные транспортные средства являются тупыми телами. ^[9] Для самолетов сопротивление давления и трения включено в определение паразитного сопротивления . Паразитное сопротивление часто выражается в терминах гипотетического.

Подъемно-индуцированное сопротивление (также называемое индуцированным сопротивлением ) — это сопротивление, которое возникает в результате создания подъемной силы на трехмерном подъемном теле , таком как крыло или пропеллер самолета. Индуцированное сопротивление состоит в основном из двух компонентов: сопротивления, вызванного созданием хвостовых вихрей ( вихревое сопротивление ); и наличия дополнительного вязкого сопротивления ( вязкое сопротивление, вызванное подъемной силой ), которое отсутствует, когда подъемная сила равна нулю. Хвостовые вихри в поле потока, присутствующие в следе за подъемным телом, возникают из-за турбулентного смешивания воздуха сверху и снизу тела, который течет в несколько разных направлениях вследствие создания подъемной силы .

При прочих равных параметрах, по мере увеличения подъемной силы, создаваемой телом, увеличивается и сопротивление, вызванное подъемной силой. Это означает, что по мере увеличения угла атаки крыла (до максимального значения, называемого углом сваливания), коэффициент подъемной силы также увеличивается, а вместе с ним и сопротивление, вызванное подъемной силой. В начале сваливания подъемная сила резко уменьшается, как и сопротивление, вызванное подъемной силой, но вязкое сопротивление давления, компонент паразитного сопротивления, увеличивается из-за образования турбулентного неприсоединенного потока в следе за телом.

Паразитное сопротивление , или профильное сопротивление, представляет собой сумму вязкого сопротивления давления ( сопротивление формы ) и сопротивления, вызванного шероховатостью поверхности ( сопротивление трения о поверхность ). Кроме того, наличие нескольких тел в относительной близости может вызвать так называемое интерференционное сопротивление , которое иногда описывается как компонент паразитного сопротивления. В аэронавтике паразитное сопротивление и сопротивление, вызванное подъемной силой, часто задаются отдельно.

Для самолета на низкой скорости индуцированное сопротивление имеет тенденцию быть относительно больше паразитного сопротивления, поскольку для поддержания подъемной силы требуется большой угол атаки , что увеличивает индуцированное сопротивление. По мере увеличения скорости угол атаки уменьшается, а индуцированное сопротивление уменьшается. Однако паразитное сопротивление увеличивается, поскольку жидкость быстрее обтекает выступающие объекты, увеличивая трение или сопротивление. На еще более высоких скоростях ( трансзвуковых ) в игру вступает волновое сопротивление . Каждая из этих форм сопротивления изменяется пропорционально другим в зависимости от скорости. Таким образом, объединенная общая кривая сопротивления показывает минимум при некоторой скорости полета — самолет, летящий на этой скорости, будет находиться на оптимальной или близкой к ней эффективности. Пилоты будут использовать эту скорость для максимизации выносливости (минимального расхода топлива) или максимизации дальности планирования в случае отказа двигателя.

Эквивалентная паразитная площадь — это площадь, которую должна была бы иметь плоская пластина, перпендикулярная потоку, чтобы соответствовать паразитному сопротивлению самолета. Это мера, используемая при сравнении сопротивления различных самолетов. Например, Douglas DC-3 имеет эквивалентную паразитную площадь 2,20 м ² (23,7 кв. фута), а McDonnell Douglas DC-9 , с 30-летним опытом в области проектирования самолетов, — площадь 1,91 м ² (20,6 кв. фута), хотя он перевозил в пять раз больше пассажиров. ^[10]

• 
  Concorde с «высоким» волновым сопротивлением хвоста
• 
  Concorde с хвостовым оперением с «низким» волновым сопротивлением (NB хвостовой шип фюзеляжа)
• 
  Самолет Hawk, показывающий базовую зону над круглым выхлопом двигателя

Сопротивление зависит от свойств жидкости и от размера, формы и скорости объекта. Один из способов выразить это — с помощью уравнения сопротивления : где$${\displaystyle F_{\mathrm {D} }\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{\mathrm {D} }\,A }$$

• ${\displaystyle F_{\rm {D}}}$это сила сопротивления ,
• ${\displaystyle \ро}$плотность жидкости, ^[11 ]
• ${\displaystyle v}$это скорость объекта относительно жидкости,
• ${\displaystyle А}$- площадь поперечного сечения , а
• ${\displaystyle C_{\rm {D}}}$коэффициент сопротивления – безразмерное число .

Коэффициент сопротивления зависит от формы объекта и от числа Рейнольдса , где$${\displaystyle \mathrm {Re} = {\frac {vD}{\nu }} = {\frac {\rho vD}{\mu }},}$$

• ${\displaystyle D}$— некоторый характерный диаметр или линейный размер . Фактически, — эквивалентный диаметр объекта. Для сферы — D самой сферы.${\displaystyle D}$ ${\displaystyle D_{e}}$${\displaystyle D_{e}}$
• Для поперечного сечения прямоугольной формы в направлении движения, где a и b — края прямоугольника.${\displaystyle D_{e}=1,30\cdot {\frac {(a\cdot b)^{0,625}}{(a+b)^{0,25}}}}$
• ${\displaystyle {\nu }}$— кинематическая вязкость жидкости (равная динамической вязкости, деленной на плотность ).${\displaystyle {\mu}}$${\displaystyle {\ро}}$

При низком значении асимптотически пропорционально , ​​что означает, что сопротивление линейно пропорционально скорости, т. е. сила сопротивления, действующая на небольшую сферу, движущуюся через вязкую жидкость, определяется законом Стокса : При высоком значении более или менее постоянна, но сопротивление будет изменяться пропорционально квадрату скорости. График справа показывает, как изменяется в случае сферы. Поскольку мощность, необходимая для преодоления силы сопротивления, является произведением силы на скорость, мощность, необходимая для преодоления сопротивления, будет изменяться пропорционально квадрату скорости при низких числах Рейнольдса и пропорционально кубу скорости при высоких числах.${\displaystyle \mathrm {Re} }$${\displaystyle C_{\rm {D}}}$${\displaystyle \mathrm {Re} ^{-1}}$$${\displaystyle F_{\rm {d}}=3\pi \mu Dv}$$${\displaystyle \mathrm {Re} }$${\displaystyle C_{\rm {D}}}$${\displaystyle C_{\rm {D}}}$${\displaystyle \mathrm {Re} }$

Можно продемонстрировать, что сила сопротивления может быть выражена как функция безразмерного числа, которое по размерности идентично числу Бежана . ^[12] Следовательно, сила сопротивления и коэффициент сопротивления могут быть функцией числа Бежана. Фактически, из выражения силы сопротивления было получено: и, следовательно, позволяет выразить коэффициент сопротивления как функцию числа Бежана и отношения между мокрой площадью и площадью фронта : ^[12] где - число Рейнольдса, связанное с длиной пути жидкости L.$${\displaystyle F_{\rm {d}}=\Delta _{\rm {p}}A_{\rm {w}}={\frac {1}{2}}C_{\rm {D}}A_{\rm {f}}{\frac {\nu \mu }{l^{2}}}\mathrm {Re} _{L}^{2}}$$ ${\displaystyle C_{\rm {D}}}$${\displaystyle A_{\rm {w}}}$${\displaystyle A_{\rm {f}}}$$${\displaystyle C_{\rm {D}}=2{\frac {A_{\rm {w}}}{A_{\rm {f}}}}{\frac {\mathrm {Be} }{\mathrm {Re} _{L}^{2}}}}$$${\displaystyle \mathrm {Re} _{L}}$

Как уже упоминалось, уравнение сопротивления с постоянным коэффициентом сопротивления дает силе, движущейся через жидкость , относительно большую скорость, т.е. высокое число Рейнольдса , Re > ~1000. Это также называется квадратичным сопротивлением .

$${\displaystyle F_{D}\,=\,{\tfrac {1}{2}}\,\rho \,v^{2}\,C_{D}\,A,}$$Вывод этого уравнения представлен в разделе Уравнение сопротивления § Вывод .

Опорная площадь A часто является ортогональной проекцией объекта или фронтальной площадью на плоскость, перпендикулярную направлению движения. Для объектов простой формы, таких как сфера, это площадь поперечного сечения . Иногда тело представляет собой композицию из различных частей, каждая из которых имеет различную опорную площадь (необходимо определить коэффициент сопротивления, соответствующий каждой из этих различных областей).

В случае крыла опорные площади одинаковы, а сила сопротивления находится в том же соотношении, что и подъемная сила . ^[13] Поэтому опорной площадью для крыла часто является подъемная площадь, иногда называемая «площадью крыла», а не лобовая площадь. ^[14]

Для объекта с гладкой поверхностью и нефиксированными точками разделения (например , сферы или кругового цилиндра) коэффициент сопротивления может изменяться в зависимости от числа Рейнольдса Re , достигая чрезвычайно высоких значений ( Re порядка 10 ⁷ ). ^{[15] [16]}

Для объекта с четко определенными фиксированными точками разделения, например, круглого диска, плоскость которого перпендикулярна направлению потока, коэффициент сопротивления постоянен при Re  > 3500. ^[16] Более того, коэффициент сопротивления C _d , как правило, является функцией ориентации потока относительно объекта (за исключением симметричных объектов, таких как сфера).

При предположении, что жидкость не движется относительно используемой в настоящее время системы отсчета, мощность , необходимая для преодоления аэродинамического сопротивления, определяется по формуле: Мощность, необходимая для проталкивания объекта через жидкость, увеличивается с увеличением куба скорости. Например, автомобилю, движущемуся по шоссе со скоростью 50 миль в час (80 км/ч), может потребоваться всего 10 лошадиных сил (7,5 кВт) для преодоления аэродинамического сопротивления, но тому же автомобилю на скорости 100 миль в час (160 км/ч) требуется 80 л. с. (60 кВт). ^[17] При удвоении скорости сопротивление/сила увеличивается в четыре раза по формуле. Приложение силы в 4 раза на фиксированном расстоянии производит в 4 раза больше работы . При удвоенной скорости работа (приводящая к перемещению на фиксированном расстоянии) выполняется в два раза быстрее. Поскольку мощность — это скорость выполнения работы, 4 раза работа, выполненная за половину времени, требует в 8 раз больше мощности.$${\displaystyle P_{D}=\mathbf {F} _{D}\cdot \mathbf {v} ={\tfrac {1}{2}}\rho v^{3}AC_{D}}$$

Когда жидкость движется относительно системы отсчета, например, автомобиль движется навстречу ветру, мощность, необходимая для преодоления аэродинамического сопротивления, определяется по следующей формуле:$${\displaystyle P_{D}=\mathbf {F} _{D}\cdot \mathbf {v_{o}} ={\tfrac {1}{2}}C_{D}A\rho (v_{w}+v_{o})^{2}v_{o}}$$

Где - скорость ветра, а - скорость объекта (обе относительно земли).${\displaystyle v_{w}}$${\displaystyle v_{o}}$

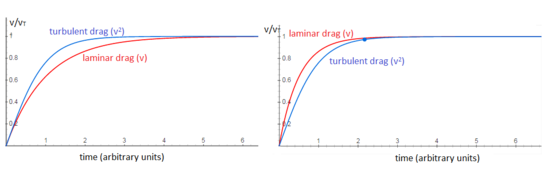
Скорость как функция времени для объекта, падающего через неплотную среду и выпущенного с нулевой относительной скоростью v  = 0 в момент времени t  = 0, приблизительно определяется функцией, содержащей гиперболический тангенс (tanh):$${\displaystyle v(t)={\sqrt {\frac {2mg}{\rho AC_{D}}}}\tanh \left(t{\sqrt {\frac {g\rho C_{D}A}{2m}}}\right).\,}$$

Гиперболический тангенс имеет предельное значение, равное единице, для большого времени t . Другими словами, скорость асимптотически приближается к максимальному значению, называемому конечной скоростью v _t :$${\displaystyle v_{t}={\sqrt {\frac {2mg}{\rho AC_{D}}}}.\,}$$

Для объекта, падающего и выпущенного с относительной скоростью v  = v _i в момент времени t  = 0, при этом v _i < v _t , также определяется через функцию гиперболического тангенса:$${\displaystyle v(t)=v_{t}\tanh \left(t{\frac {g}{v_{t}}}+\operatorname {arctanh} \left({\frac {v_{i}}{v_{t}}}\right)\right).\,}$$

При v _i > v _t функция скорости определяется через функцию гиперболического котангенса :$${\displaystyle v(t)=v_{t}\coth \left(t{\frac {g}{v_{t}}}+\coth ^{-1}\left({\frac {v_{i}}{v_{t}}}\right)\right).\,}$$

Гиперболический котангенс также имеет предельное значение, равное единице, для больших времен t . Скорость асимптотически стремится к конечной скорости v _t , строго сверху v _t .

При v _i = v _t скорость постоянна:$${\displaystyle v(t)=v_{t}.}$$

Эти функции определяются решением следующего дифференциального уравнения :$${\displaystyle g-{\frac {\rho AC_{D}}{2m}}v^{2}={\frac {dv}{dt}}.\,}$$

Или, в более общем виде (где F ( v ) — силы, действующие на объект помимо сопротивления):$${\displaystyle {\frac {1}{m}}\sum F(v)-{\frac {\rho AC_{D}}{2m}}v^{2}={\frac {dv}{dt}}.\,}$$

Для объекта в форме картофеля со средним диаметром d и плотностью ρ _obj конечная скорость составляет около$${\displaystyle v_{t}={\sqrt {gd{\frac {\rho _{obj}}{\rho }}}}.\,}$$

Для объектов с плотностью, подобной плотности воды (капли дождя, град, живые объекты — млекопитающие, птицы, насекомые и т. д.), падающих в воздухе вблизи поверхности Земли на уровне моря, конечная скорость примерно равна с d в метрах и v _t в м/с. Например, для человеческого тела ( ≈0,6 м) ≈70 м/с, для небольшого животного, такого как кошка ( ≈0,2 м) ≈40 м/с, для небольшой птицы ( ≈0,05 м) ≈20 м/с, для насекомого ( ≈0,01 м) ≈9 м/с и т. д. Конечная скорость для очень малых объектов (пыльца и т. д.) при малых числах Рейнольдса определяется законом Стокса.$${\displaystyle v_{t}=90{\sqrt {d}},\,}$$${\displaystyle d}$${\displaystyle v_{t}}$${\displaystyle d}$${\displaystyle v_{t}}$${\displaystyle d}$${\displaystyle v_{t}}$${\displaystyle d}$${\displaystyle v_{t}}$

Короче говоря, конечная скорость выше для более крупных существ, и, таким образом, потенциально более смертоносна. Существо, такое как мышь, падающее с конечной скоростью, имеет гораздо больше шансов выжить при ударе о землю, чем человек, падающий с конечной скоростью. ^[18]

Уравнение для вязкого сопротивления или линейного сопротивления подходит для объектов или частиц, движущихся через жидкость с относительно низкой скоростью (при условии отсутствия турбулентности). Чисто ламинарный поток существует только до Re = 0,1 согласно этому определению. В этом случае сила сопротивления приблизительно пропорциональна скорости. Уравнение для вязкого сопротивления имеет вид: ^[19]

$${\displaystyle \mathbf {F} _{D}=-b\mathbf {v} \,}$$

где:

• ${\displaystyle b}$— константа, зависящая как от материальных свойств объекта и жидкости, так и от геометрии объекта; и
• ${\displaystyle \mathbf {v} }$это скорость объекта.

Когда объект падает из состояния покоя, его скорость будет равна:$${\displaystyle v(t)={\frac {(\rho -\rho _{0})\,V\,g}{b}}\left(1-e^{-b\,t/m}\right)}$$

• ${\displaystyle \rho }$это плотность объекта,
• ${\displaystyle \rho _{0}}$плотность жидкости,
• ${\displaystyle V}$объем объекта,
• ${\displaystyle g}$это ускорение свободного падения (т.е. 9,8 м/с ), и${\displaystyle ^{2}}$
• ${\displaystyle m}$масса объекта.

Скорость асимптотически приближается к конечной скорости . При заданном более плотные объекты падают быстрее.${\displaystyle v_{t}={\frac {(\rho -\rho _{0})Vg}{b}}}$${\displaystyle b}$

Для особого случая небольших сферических объектов, медленно движущихся в вязкой жидкости (и, следовательно, при малых числах Рейнольдса), Джордж Габриэль Стокс вывел выражение для константы сопротивления: где — радиус Стокса частицы, а — вязкость жидкости .$${\displaystyle b=6\pi \eta r\,}$$${\displaystyle r}$${\displaystyle \eta }$

Полученное выражение для сопротивления известно как сопротивление Стокса : ^[20]$${\displaystyle \mathbf {F} _{D}=-6\pi \eta r\,\mathbf {v} .}$$

Например, рассмотрим небольшую сферу с радиусом = 0,5 микрометра (диаметр = 1,0 мкм), движущуюся в воде со скоростью 10 мкм/с. Используя 10−3 ^Па ·с в качестве динамической вязкости воды в единицах СИ, мы находим силу сопротивления 0,09 пН. Это примерно сила сопротивления, которую испытывает бактерия, плывущая в воде.${\displaystyle r}$${\displaystyle v}$

Коэффициент сопротивления сферы можно определить для общего случая ламинарного течения при числах Рейнольдса меньше, используя следующую формулу: ^[21]${\displaystyle 2\cdot 10^{5}}$

$${\displaystyle C_{D}={\frac {24}{Re}}+{\frac {4}{\sqrt {Re}}}+0.4~{\text{;}}~~~~~Re<2\cdot 10^{5}}$$

При числах Рейнольдса меньше 1 применяется закон Стокса, а коэффициент сопротивления приближается к !${\displaystyle {\frac {24}{Re}}}$

В аэродинамике аэродинамическое сопротивление , также известное как сопротивление воздуха , представляет собой силу сопротивления жидкости, которая действует на любое движущееся твердое тело в направлении свободного потока воздуха. ^[22]

• С точки зрения тела (приближение ближнего поля) сопротивление возникает из-за сил, обусловленных распределением давления по поверхности тела, что символизируется .${\displaystyle D_{pr}}$
• Силы, возникающие из-за трения поверхности, которое является результатом вязкости, обозначаются .${\displaystyle D_{f}}$

Альтернативно, при расчете с точки зрения поля потока (подход дальнего поля) сила сопротивления является результатом трех естественных явлений: ударных волн , вихревой пелены и вязкости .

Когда самолет создает подъемную силу, возникает другой компонент сопротивления. Индуцированное сопротивление , обозначенное символом , возникает из-за изменения распределения давления из-за системы вихрей, которая сопровождает создание подъемной силы. Альтернативный взгляд на подъемную силу и сопротивление достигается путем рассмотрения изменения импульса воздушного потока. Крыло перехватывает воздушный поток и заставляет поток двигаться вниз. Это приводит к возникновению равной и противоположной силы, действующей вверх на крыло, которая является подъемной силой. Изменение импульса воздушного потока вниз приводит к уменьшению направленного назад импульса потока, что является результатом силы, действующей вперед на воздушный поток и приложенной крылом к ​​воздушному потоку; равная, но противоположная сила действует на крыло сзади, что является индуцированным сопротивлением. Другой компонент сопротивления, а именно волновое сопротивление , , возникает из-за ударных волн на околозвуковых и сверхзвуковых скоростях полета. Ударные волны вызывают изменения в пограничном слое и распределении давления по поверхности тела.${\displaystyle D_{i}}$${\displaystyle D_{w}}$

Таким образом, существует три способа классификации сопротивления. ^{[23] : 19}

1. Сопротивление давления и сопротивление трения
2. Профильное сопротивление и индуцированное сопротивление
3. Вихревое сопротивление, волновое сопротивление и сопротивление следа

Распределение давления, действующее на поверхность тела, оказывает на тело нормальные силы. Эти силы можно сложить, и компонент этой силы, действующий вниз по потоку, представляет собой силу сопротивления, . Природа этих нормальных сил сочетает в себе эффекты ударной волны, эффекты генерации вихревой системы и механизмы вязкости следа.${\displaystyle D_{pr}}$

Вязкость жидкости оказывает большое влияние на сопротивление. При отсутствии вязкости силы давления, препятствующие движению транспортного средства, нейтрализуются силой давления, действующей дальше сзади, которая толкает транспортное средство вперед; это называется восстановлением давления, и в результате сопротивление равно нулю. То есть работа, которую тело выполняет над потоком воздуха, обратима и восстанавливается, поскольку нет никаких эффектов трения, которые могли бы преобразовать энергию потока в тепло. Восстановление давления действует даже в случае вязкого потока. Однако вязкость приводит к сопротивлению давления и является доминирующим компонентом сопротивления в случае транспортных средств с областями разделенного потока, в которых восстановление давления является заразным.

Сила сопротивления трения, которая является тангенциальной силой на поверхности самолета, существенно зависит от конфигурации пограничного слоя и вязкости. Чистое сопротивление трения, , рассчитывается как проекция вниз по потоку вязких сил, оцененных по поверхности тела. Сумма сопротивления трения и сопротивления давления (формы) называется вязким сопротивлением. Этот компонент сопротивления обусловлен вязкостью. ${\displaystyle D_{f}}$

Идея о том, что движущееся тело, проходящее через воздух или другую жидкость, встречает сопротивление, была известна со времен Аристотеля . По словам Мервина О'Гормана , это было названо «сопротивлением» Арчибальдом Рейтом Лоу . ^{[24] Статья} Луи Шарля Бреге 1922 года положила начало попыткам уменьшить сопротивление путем обтекаемости. ^[25] Бреге продолжил воплощать свои идеи в жизнь, спроектировав несколько рекордных самолетов в 1920-х и 1930-х годах. Теория пограничного слоя Людвига Прандтля в 1920-х годах дала толчок к минимизации трения поверхности. Еще один важный призыв к обтекаемости был сделан сэром Мелвиллом Джонсом , который представил теоретические концепции, чтобы наглядно продемонстрировать важность обтекаемости в проектировании самолетов . ^{[26] [27] [28]} В 1929 году его статья «Обтекаемый самолет», представленная Королевскому авиационному обществу, была основополагающей. Он предложил идеальный самолет, который имел бы минимальное сопротивление, что привело к концепциям «чистого» моноплана и убирающегося шасси . Аспектом статьи Джонса, который больше всего шокировал конструкторов того времени, был его график требуемой мощности в зависимости от скорости для реального и идеального самолета. Рассматривая точку данных для данного самолета и экстраполируя ее горизонтально на идеальную кривую, можно увидеть прирост скорости для той же мощности. Когда Джонс закончил свою презентацию, один из присутствующих описал результаты как имеющие тот же уровень важности, что и цикл Карно в термодинамике. ^{[25] [26]}

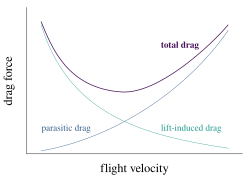
Взаимодействие паразитного и индуцированного сопротивления с воздушной скоростью можно изобразить в виде характеристической кривой, проиллюстрированной здесь. В авиации это часто называют кривой мощности , и она важна для пилотов, поскольку она показывает, что ниже определенной воздушной скорости поддержание воздушной скорости вопреки интуиции требует большей тяги по мере снижения скорости, а не меньшей. Последствия нахождения «за кривой» в полете важны и изучаются как часть обучения пилотов. На дозвуковых воздушных скоростях, где форма «U» этой кривой является значительной, волновое сопротивление еще не стало фактором, и поэтому оно не показано на кривой.

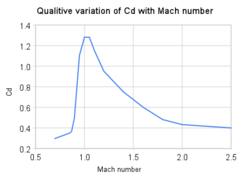
Волновое сопротивление, иногда называемое сопротивлением сжимаемости, — это сопротивление, которое возникает, когда тело движется в сжимаемой жидкости со скоростью, близкой к скорости звука в этой жидкости. В аэродинамике волновое сопротивление состоит из нескольких компонентов, зависящих от скоростного режима полета.

В околозвуковом полете волновое сопротивление является результатом образования ударных волн в жидкости, образующихся при создании локальных областей сверхзвукового (число Маха больше 1,0) потока. На практике сверхзвуковой поток возникает на телах, движущихся значительно ниже скорости звука, поскольку локальная скорость воздуха увеличивается по мере его ускорения над телом до скоростей выше 1,0 Маха. Однако полный сверхзвуковой поток над транспортным средством не разовьется, пока не превысит 1,0 Маха. Самолеты, летящие на околозвуковой скорости, часто подвергаются волновому сопротивлению в ходе нормальной эксплуатации. В околозвуковом полете волновое сопротивление обычно называют сопротивлением околозвуковой сжимаемости . Сопротивление околозвуковой сжимаемости значительно увеличивается по мере увеличения скорости полета до 1,0 Маха, доминируя над другими формами сопротивления на этих скоростях.

В сверхзвуковом полете (числа Маха больше 1,0) волновое сопротивление является результатом ударных волн, присутствующих в жидкости и прикрепленных к телу, обычно косых ударных волн, образующихся на передней и задней кромках тела. В сильно сверхзвуковых потоках или в телах с достаточно большими углами поворота вместо этого образуются неприкрепленные ударные волны или носовые волны . Кроме того, локальные области околозвукового потока за начальной ударной волной могут возникать при более низких сверхзвуковых скоростях и могут приводить к развитию дополнительных, меньших ударных волн, присутствующих на поверхностях других подъемных тел, подобных тем, которые обнаруживаются в околозвуковых потоках. В режимах сверхзвукового потока волновое сопротивление обычно разделяется на два компонента: сверхзвуковое волновое сопротивление, зависящее от подъемной силы , и сверхзвуковое волновое сопротивление, зависящее от объема .

Замкнутая форма решения для минимального волнового сопротивления тела вращения с фиксированной длиной была найдена Сирсом и Хааком и известна как распределение Сирса-Хаака . Аналогично, для фиксированного объема форма для минимального волнового сопротивления — это оживальное уравнение фон Кармана .

Теоретическая концепция биплана Буземана не подвержена волновому сопротивлению при движении на расчетной скорости, но не способна создавать подъемную силу в этих условиях.

В 1752 году Даламбер доказал, что потенциальный поток , современная теория невязкого потока XVIII века , поддающаяся математическим решениям, привела к предсказанию нулевого сопротивления. Это противоречило экспериментальным данным и стало известно как парадокс Даламбера. В XIX веке уравнения Навье-Стокса для описания вязкого потока были разработаны Сен-Венаном , Навье и Стоксом . Стокс вывел сопротивление вокруг сферы при очень низких числах Рейнольдса , результат которого называется законом Стокса . ^[29]

В пределе высоких чисел Рейнольдса уравнения Навье–Стокса приближаются к невязким уравнениям Эйлера , решениями которых являются решения потенциального течения, рассмотренные Даламбером. Однако все эксперименты при высоких числах Рейнольдса показали, что сопротивление есть. Попытки построить невязкие стационарные решения течения для уравнений Эйлера, отличные от решений потенциального течения, не привели к реалистичным результатам. ^[29]

Понятие пограничных слоев , введенное Прандтлем в 1904 году, основанное как на теории, так и на экспериментах, объяснило причины сопротивления при высоких числах Рейнольдса. Пограничный слой — это тонкий слой жидкости вблизи границы объекта, где вязкие эффекты остаются важными, даже когда вязкость очень мала (или, что эквивалентно, число Рейнольдса очень велико). ^[29]

• «Улучшенная эмпирическая модель для прогнозирования сопротивления основания ракетных конфигураций на основе новых данных аэродинамической трубы», Фрэнк Г. Мур и др., NASA Langley Center
• «Расчетное исследование снижения лобового сопротивления снаряда на различных режимах полета», М.А. Сулиман и др. Труды 13-й Международной конференции по аэрокосмическим наукам и авиационным технологиям, ASAT-13, 26–28 мая 2009 г.
• «Сопротивление основания и толстые задние кромки», Зигхард Ф. Хорнер, Командование материально-технического обеспечения ВВС, в: Журнал авиационных наук, октябрь 1950 г., стр. 622–628

• Френч, AP (1970). Ньютоновская механика (серия «Введение в физику» Массачусетского технологического института) (1-е изд.). WW White & Company Inc., Нью-Йорк. ISBN 978-0-393-09958-4.
• Г. Фалькович (2011). Механика жидкости (Краткий курс для физиков). Cambridge University Press. ISBN 978-1-107-00575-4.
• Serway, Raymond A.; Jewett, John W. (2004). Физика для ученых и инженеров (6-е изд.). Brooks/Cole. ISBN 978-0-534-40842-8.
• Типлер, Пол (2004). Физика для ученых и инженеров: механика, колебания и волны, термодинамика (5-е изд.). WH Freeman. ISBN 978-0-7167-0809-4.
• Хантли, Х. Э. (1967). Анализ размеров . LOC 67-17978.
• Бэтчелор, Джордж (2000). Введение в гидродинамику . Кембриджская математическая библиотека (2-е изд.). Cambridge University Press . ISBN 978-0-521-66396-0. МР  1744638.
• LJ Clancy (1975), Аэродинамика , Pitman Publishing Limited, Лондон. ISBN 978-0-273-01120-0 
• Андерсон, Джон Д. младший (2000); Введение в полет , четвертое издание, McGraw Hill Higher Education, Бостон, Массачусетс, США. 8-е изд. 2015, ISBN 978-0078027673 . 

• Образовательные материалы по сопротивлению воздуха
• Аэродинамическое сопротивление и его влияние на ускорение и максимальную скорость транспортного средства.
• Калькулятор аэродинамического сопротивления транспортного средства на основе коэффициента сопротивления, лобовой площади и скорости.
• Сайт Смитсоновского национального музея авиации и космонавтики How Things Fly
• Эффект ямочек на мяче для гольфа и автомобиле