Суммирование

Арифметические операции в т е

Дополнение (+) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{term}}\,+\,{\text{term}}\\\scriptstyle {\text{summand}}\,+\,{\text{summand}}\\\scriptstyle {\text{addend}}\,+\,{\text{addend}}\\\scriptstyle {\text{augend}}\,+\,{\text{addend}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{сумма}}}$ Вычитание (−) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{term}}\,-\,{\text{term}}\\\scriptstyle {\text{minuend}}\,-\,{\text{subtrahend}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{разница}}}$ Умножение (×) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{factor}}\,\times \,{\text{factor}}\\\scriptstyle {\text{multiplier}}\,\times \,{\text{multiplicand}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{продукт}}}$ Деление (÷) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\frac {\scriptstyle {\text{делимое}}}{\scriptstyle {\text{делитель}}}}\\[1ex]\scriptstyle {\frac {\scriptstyle {\text{числитель}}}{\scriptstyle {\text{знаменатель}}}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle \left\{{\begin{matrix}\scriptstyle {\text{fraction}}\\\scriptstyle {\text{quotient}}\\\scriptstyle {\text{ratio}}\end{matrix}}\right.}$ Возведение в степень (^) ${\displaystyle \scriptstyle \left.{\begin{matrix}\scriptstyle {\text{base}}^{\text{exponent}}\\\scriptstyle {\text{base}}^{\text{power}}\end{matrix}}\right\}\,=\,}$ ${\displaystyle \scriptstyle {\text{мощность}}}$ корень n- й степени (√) ${\displaystyle \scriptstyle {\sqrt[{\text{степень}}]{\scriptstyle {\text{подкоренное число}}}}\,=\,}$ ${\displaystyle \scriptstyle {\text{корень}}}$ Логарифм (log) ${\displaystyle \scriptstyle \log _{\text{основание}}({\text{антилогарифм}})\,=\,}$ ${\displaystyle \scriptstyle {\text{логарифм}}}$

в т е

В математике суммирование — это сложение последовательности чисел , называемых слагаемыми или аддендами ; результатом является их сумма или итог . Помимо чисел , можно суммировать и другие типы значений: функции , векторы , матрицы , многочлены и, в общем, элементы любого типа математических объектов, над которыми определена операция, обозначенная «+» .

Суммирование бесконечных последовательностей называется сериями . Они включают в себя понятие предела и не рассматриваются в этой статье.

Суммирование явной последовательности обозначается как последовательность сложений. Например, суммирование [1, 2, 4, 2] обозначается как 1 + 2 + 4 + 2 и дает в результате 9, то есть 1 + 2 + 4 + 2 = 9. Поскольку сложение ассоциативно и коммутативно , скобки не нужны, и результат тот же, независимо от порядка слагаемых. Суммирование последовательности только из одного слагаемого дает в результате само слагаемое. Суммирование пустой последовательности (последовательности без элементов) по соглашению дает в результате 0.

Очень часто элементы последовательности определяются через регулярный шаблон как функция их места в последовательности. Для простых шаблонов суммирование длинных последовательностей может быть представлено с заменой большинства слагаемых многоточиями. Например, суммирование первых 100 натуральных чисел может быть записано как 1 + 2 + 3 + 4 + ⋯ + 99 + 100 . В противном случае суммирование обозначается с помощью обозначения Σ, где — увеличенная заглавная греческая буква сигма . Например, сумму первых n натуральных чисел можно обозначить как${\textstyle \сумма}$

${\displaystyle \sum _{i=1}^{n}i}$

Для длинных сумм и сумм переменной длины (определяемых с помощью многоточия или Σ-обозначения) часто возникает проблема поиска выражений в замкнутой форме для результата. Например, ^[a]

${\displaystyle \sum _{i=1}^{n}i={\frac {n(n+1)}{2}}.}$

Хотя такие формулы не всегда существуют, было обнаружено много формул суммирования, некоторые из наиболее распространенных и элементарных из которых перечислены в оставшейся части этой статьи.

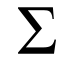
Математическая нотация использует символ, который компактно представляет сумму многих подобных терминов: символ суммы , , увеличенная форма вертикальной заглавной греческой буквы сигма . ^[1] Это определяется как${\textstyle \сумма}$

${\displaystyle \sum _{i\mathop {=} m}^{n}a_{i}=a_{m}+a_{m+1}+a_{m+2}+\cdots +a_{n-1}+a_{n}}$

где i — индекс суммирования ; a _i — индексированная переменная, представляющая каждый член суммы; m — нижняя граница суммирования , а n — верхняя граница суммирования . « i = m » под символом суммирования означает, что индекс i изначально равен m . Индекс i увеличивается на единицу для каждого последующего члена, останавливаясь, когда i = n . ^[b]

Это читается как «сумма a _i , от i = m до n ».

Вот пример, показывающий суммирование квадратов:

${\displaystyle \sum _{i=3}^{6}i^{2}=3^{2}+4^{2}+5^{2}+6^{2}=86.}$

В целом, хотя в качестве индекса суммирования может использоваться любая переменная (при условии отсутствия двусмысленности), некоторые из наиболее распространенных включают в себя такие буквы, как , ^[c] , , и ; последняя также часто используется для верхней границы суммирования.${\displaystyle я}$ ${\displaystyle j}$${\displaystyle к}$${\displaystyle n}$

В качестве альтернативы, индекс и границы суммирования иногда опускаются из определения суммирования, если контекст достаточно ясен. Это применимо, в частности, когда индекс идет от 1 до n . ^[2] Например, можно написать, что:

${\displaystyle \sum a_{i}^{2}=\sum _{i=1}^{n}a_{i}^{2}.}$

Часто используются обобщения этой нотации, в которых задается произвольное логическое условие, а сумма должна быть взята по всем значениям, удовлетворяющим условию. Например:

${\displaystyle \sum _{0\leq k<100}f(k)}$

является альтернативной записью для суммы всех ( целых чисел ) в указанном диапазоне. Аналогично,${\textstyle \sum _{k=0}^{99}f(k),}$${\displaystyle f(k)}$${\displaystyle k}$

${\displaystyle \sum _{x\mathop {\in } S}f(x)}$

это сумма по всем элементам в наборе , и${\displaystyle f(x)}$${\displaystyle x}$${\displaystyle S}$

${\displaystyle \sum _{d\,|\,n}\;\mu (d)}$

это сумма всех положительных целых чисел, делящихся на . ^[d]${\displaystyle \mu (d)}$${\displaystyle d}$ ${\displaystyle n}$

Существуют также способы обобщения использования многих знаков сигмы. Например,

${\displaystyle \sum _{i,j}}$

то же самое, что и

${\displaystyle \sum _{i}\sum _{j}.}$

Аналогичное обозначение используется для произведения последовательности , где вместо используется увеличенная форма греческой заглавной буквы пи .${\textstyle \prod }$${\textstyle \sum .}$

Можно сложить менее 2 чисел:

• Если в сумме имеется одно слагаемое , то оценённая сумма равна .${\displaystyle x}$${\displaystyle x}$
• Если в суммировании нет слагаемых, то оцененная сумма равна нулю , поскольку ноль является тождеством для сложения. Это известно как пустая сумма .

Эти вырожденные случаи обычно используются только тогда, когда запись суммирования дает вырожденный результат в особом случае. Например, если в определении выше, то в сумме есть только один член; если , то нет ни одного.${\displaystyle n=m}$${\displaystyle n=m-1}$

Фраза «алгебраическая сумма» относится к сумме членов, которые могут иметь положительные или отрицательные знаки. Члены с положительными знаками складываются, а члены с отрицательными знаками вычитаются.

Суммирование можно определить рекурсивно следующим образом:

${\displaystyle \sum _{i=a}^{b}g(i)=0}$, для ;${\displaystyle b<a}$

${\displaystyle \sum _{i=a}^{b}g(i)=g(b)+\sum _{i=a}^{b-1}g(i)}$, для .${\displaystyle b\geqslant a}$

В обозначениях теории меры и интегрирования сумма может быть выражена как определенный интеграл ,

${\displaystyle \sum _{k\mathop {=} a}^{b}f(k)=\int _{[a,b]}f\,d\mu }$

где — подмножество целых чисел от до , а где — мера подсчета целых чисел.${\displaystyle [a,b]}$${\displaystyle a}$${\displaystyle b}$${\displaystyle \mu }$

Для функции f , определенной над целыми числами в интервале [ m , n ] , справедливо следующее уравнение:

${\displaystyle f(n)-f(m)=\sum _{i=m}^{n-1}(f(i+1)-f(i)).}$

Это известно как телескопический ряд и является аналогом основной теоремы исчисления в исчислении конечных разностей , которая гласит:

${\displaystyle f(n)-f(m)=\int _{m}^{n}f'(x)\,dx,}$

где

${\displaystyle f'(x)=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}}$

является производной от f .

Примером применения приведенного выше уравнения является следующее:

${\displaystyle n^{k}=\sum _{i=0}^{n-1}\left((i+1)^{k}-i^{k}\right).}$

Используя биномиальную теорему , это можно переписать так:

${\displaystyle n^{k}=\sum _{i=0}^{n-1}{\biggl (}\sum _{j=0}^{k-1}{\binom {k}{j}}i^{j}{\biggr )}.}$

Приведенная выше формула чаще используется для инвертирования оператора разности , определяемого как:${\displaystyle \Delta }$

${\displaystyle \Delta (f)(n)=f(n+1)-f(n),}$

где f — функция, определенная на неотрицательных целых числах. Таким образом, при наличии такой функции f проблема состоит в вычислении антиразности f , функции такой, что . То есть, Эта функция определена с точностью до добавления константы и может быть выбрана как [ ^3]${\displaystyle F=\Delta ^{-1}f}$${\displaystyle \Delta F=f}$${\displaystyle F(n+1)-F(n)=f(n).}$

${\displaystyle F(n)=\sum _{i=0}^{n-1}f(i).}$

Не всегда существует замкнутое выражение для такого суммирования, но формула Фаульхабера дает замкнутую форму в случае, когда и, в силу линейности , для каждой полиномиальной функции от n .${\displaystyle f(n)=n^{k}}$

Многие такие приближения можно получить с помощью следующей связи между суммами и интегралами , которая справедлива для любой возрастающей функции f :

${\displaystyle \int _{s=a-1}^{b}f(s)\ ds\leq \sum _{i=a}^{b}f(i)\leq \int _{s=a}^{b+1}f(s)\ ds.}$

и для любой убывающей функции f :

${\displaystyle \int _{s=a}^{b+1}f(s)\ ds\leq \sum _{i=a}^{b}f(i)\leq \int _{s=a-1}^{b}f(s)\ ds.}$

Для более общих приближений см. формулу Эйлера–Маклорена .

Для сумм, в которых слагаемое задано (или может быть интерполировано) интегрируемой функцией индекса, суммирование можно интерпретировать как сумму Римана, встречающуюся в определении соответствующего определенного интеграла. Поэтому можно ожидать, что, например,

${\displaystyle {\frac {b-a}{n}}\sum _{i=0}^{n-1}f\left(a+i{\frac {b-a}{n}}\right)\approx \int _{a}^{b}f(x)\ dx,}$

поскольку правая часть по определению является пределом для левой части. Однако для заданного суммирования n фиксировано, и мало что можно сказать об ошибке в приведенном выше приближении без дополнительных предположений относительно f : ясно, что для сильно колеблющихся функций сумма Римана может быть сколь угодно далека от интеграла Римана.${\displaystyle n\to \infty }$

Приведенные ниже формулы содержат конечные суммы; для бесконечных сумм или конечных сумм выражений, содержащих тригонометрические функции или другие трансцендентные функции , см. список математических рядов .

${\displaystyle \sum _{n=s}^{t}C\cdot f(n)=C\cdot \sum _{n=s}^{t}f(n)\quad }$( распределительность ) ^[4]

${\displaystyle \sum _{n=s}^{t}f(n)\pm \sum _{n=s}^{t}g(n)=\sum _{n=s}^{t}\left(f(n)\pm g(n)\right)\quad }$( коммутативность и ассоциативность ) ^[4]

${\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=s+p}^{t+p}f(n-p)\quad }$(сдвиг индекса)

${\displaystyle \sum _{n\in B}f(n)=\sum _{m\in A}f(\sigma (m)),\quad }$для биекции σ из конечного множества A на множество B (изменение индекса); это обобщает предыдущую формулу.

${\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=s}^{j}f(n)+\sum _{n=j+1}^{t}f(n)\quad }$(разделение суммы, используя ассоциативность )

${\displaystyle \sum _{n=a}^{b}f(n)=\sum _{n=0}^{b}f(n)-\sum _{n=0}^{a-1}f(n)\quad }$(вариант предыдущей формулы)

${\displaystyle \sum _{n=s}^{t}f(n)=\sum _{n=0}^{t-s}f(t-n)\quad }$(сумма от первого члена до последнего равна сумме от последнего до первого)

${\displaystyle \sum _{n=0}^{t}f(n)=\sum _{n=0}^{t}f(t-n)\quad }$(частный случай формулы выше)

${\displaystyle \sum _{i=k_{0}}^{k_{1}}\sum _{j=l_{0}}^{l_{1}}a_{i,j}=\sum _{j=l_{0}}^{l_{1}}\sum _{i=k_{0}}^{k_{1}}a_{i,j}\quad }$(снова коммутативность и ассоциативность)

${\displaystyle \sum _{k\leq j\leq i\leq n}a_{i,j}=\sum _{i=k}^{n}\sum _{j=k}^{i}a_{i,j}=\sum _{j=k}^{n}\sum _{i=j}^{n}a_{i,j}=\sum _{j=0}^{n-k}\sum _{i=k}^{n-j}a_{i+j,i}\quad }$(еще одно применение коммутативности и ассоциативности)

${\displaystyle \sum _{n=2s}^{2t+1}f(n)=\sum _{n=s}^{t}f(2n)+\sum _{n=s}^{t}f(2n+1)\quad }$(разделение суммы на четную и нечетную части, для четных индексов)

${\displaystyle \sum _{n=2s+1}^{2t}f(n)=\sum _{n=s+1}^{t}f(2n)+\sum _{n=s+1}^{t}f(2n-1)\quad }$(разделение суммы на четную и нечетную части, для нечетных индексов)

${\displaystyle {\biggl (}\sum _{i=0}^{n}a_{i}{\biggr )}{\biggl (}\sum _{j=0}^{n}b_{j}{\biggr )}=\sum _{i=0}^{n}\sum _{j=0}^{n}a_{i}b_{j}\quad }$( распределительность )

${\displaystyle \sum _{i=s}^{m}\sum _{j=t}^{n}{a_{i}}{c_{j}}={\biggl (}\sum _{i=s}^{m}a_{i}{\biggr )}{\biggl (}\sum _{j=t}^{n}c_{j}{\biggr )}\quad }$(дистрибутивность допускает факторизацию)

${\displaystyle \sum _{n=s}^{t}\log _{b}f(n)=\log _{b}\prod _{n=s}^{t}f(n)\quad }$( логарифм произведения равен сумме логарифмов множителей)

${\displaystyle C^{\sum \limits _{n=s}^{t}f(n)}=\prod _{n=s}^{t}C^{f(n)}\quad }$( экспонента суммы — это произведение экспонент слагаемых)

${\displaystyle \sum _{m=0}^{k}\sum _{n=0}^{m}f(m,n)=\sum _{m=0}^{k}\sum _{n=m}^{k}f(n,m),\quad }$для любой функции из .${\textstyle f}$${\textstyle \mathbb {Z} \times \mathbb {Z} }$

${\displaystyle \sum _{i=1}^{n}c=nc\quad }$для каждого c, который не зависит от i

${\displaystyle \sum _{i=0}^{n}i=\sum _{i=1}^{n}i={\frac {n(n+1)}{2}}\qquad }$(Сумма простейшей арифметической прогрессии , состоящей из первых n натуральных чисел.) ^{[3] : 52}

${\displaystyle \sum _{i=1}^{n}(2i-1)=n^{2}\qquad }$(Сумма первых нечетных натуральных чисел)

${\displaystyle \sum _{i=0}^{n}2i=n(n+1)\qquad }$(Сумма первых четных натуральных чисел)

${\displaystyle \sum _{i=1}^{n}\log i=\log n!\qquad }$(Сумма логарифмов равна логарифму произведения)

${\displaystyle \sum _{i=0}^{n}i^{2}=\sum _{i=1}^{n}i^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}}\qquad }$(Сумма первых квадратов , см. квадратное пирамидальное число .) ^{[3] : 52}

${\displaystyle \sum _{i=0}^{n}i^{3}={\biggl (}\sum _{i=0}^{n}i{\biggr )}^{2}=\left({\frac {n(n+1)}{2}}\right)^{2}={\frac {n^{4}}{4}}+{\frac {n^{3}}{2}}+{\frac {n^{2}}{4}}\qquad }$( Теорема Никомаха ) ^{[3] : 52}

В более общем смысле, есть формула Фаульхабера для${\displaystyle p>1}$

${\displaystyle \sum _{k=1}^{n}k^{p}={\frac {n^{p+1}}{p+1}}+{\frac {1}{2}}n^{p}+\sum _{k=2}^{p}{\binom {p}{k}}{\frac {B_{k}}{p-k+1}}\,n^{p-k+1},}$

где обозначает число Бернулли , а — биномиальный коэффициент .${\displaystyle B_{k}}$${\displaystyle {\binom {p}{k}}}$

В следующих вычислениях предполагается, что a отличается от 1.

${\displaystyle \sum _{i=0}^{n-1}a^{i}={\frac {1-a^{n}}{1-a}}}$(сумма геометрической прогрессии )

${\displaystyle \sum _{i=0}^{n-1}{\frac {1}{2^{i}}}=2-{\frac {1}{2^{n-1}}}}$(частный случай для a = 1/2 )

${\displaystyle \sum _{i=0}^{n-1}ia^{i}={\frac {a-na^{n}+(n-1)a^{n+1}}{(1-a)^{2}}}}$( а умножить на производную по а геометрической прогрессии)

${\displaystyle {\begin{aligned}\sum _{i=0}^{n-1}\left(b+id\right)a^{i}&=b\sum _{i=0}^{n-1}a^{i}+d\sum _{i=0}^{n-1}ia^{i}\\&=b\left({\frac {1-a^{n}}{1-a}}\right)+d\left({\frac {a-na^{n}+(n-1)a^{n+1}}{(1-a)^{2}}}\right)\\&={\frac {b(1-a^{n})-(n-1)da^{n}}{1-a}}+{\frac {da(1-a^{n-1})}{(1-a)^{2}}}\end{aligned}}}$

(сумма арифметико–геометрической прогрессии )

Существует очень много тождеств суммирования, включающих биномиальные коэффициенты (целая глава Конкретной математики посвящена только базовым методам). Вот некоторые из самых базовых.

${\displaystyle \sum _{i=0}^{n}{n \choose i}a^{n-i}b^{i}=(a+b)^{n},}$биномиальная теорема

${\displaystyle \sum _{i=0}^{n}{n \choose i}=2^{n},}$особый случай, когда a = b = 1

${\displaystyle \sum _{i=0}^{n}{n \choose i}p^{i}(1-p)^{n-i}=1}$, частный случай, когда p = a = 1 − b , который для выражает сумму биномиального распределения${\displaystyle 0\leq p\leq 1,}$

${\displaystyle \sum _{i=0}^{n}i{n \choose i}=n(2^{n-1}),}$значение при a = b = 1 производной по a биномиальной теоремы

${\displaystyle \sum _{i=0}^{n}{\frac {n \choose i}{i+1}}={\frac {2^{n+1}-1}{n+1}},}$значение при a = b = 1 первообразной по a биномиальной теоремы

В следующих суммированиях — число k -перестановок n .${\displaystyle {}_{n}P_{k}}$

${\displaystyle \sum _{i=0}^{n}{}_{i}P_{k}{n \choose i}={}_{n}P_{k}(2^{n-k})}$

${\displaystyle \sum _{i=1}^{n}{}_{i+k}P_{k+1}=\sum _{i=1}^{n}\prod _{j=0}^{k}(i+j)={\frac {(n+k+1)!}{(n-1)!(k+2)}}}$

${\displaystyle \sum _{i=0}^{n}i!\cdot {n \choose i}=\sum _{i=0}^{n}{}_{n}P_{i}=\lfloor n!\cdot e\rfloor ,\quad n\in \mathbb {Z} ^{+}}$, где и обозначает функцию пола .${\displaystyle \lfloor x\rfloor }$

${\displaystyle \sum _{k=0}^{m}{\binom {n+k}{n}}={\binom {n+m+1}{n+1}}}$

${\displaystyle \sum _{i=k}^{n}{i \choose k}={n+1 \choose k+1}}$

${\displaystyle \sum _{i=0}^{n}i\cdot i!=(n+1)!-1}$

${\displaystyle \sum _{i=0}^{n}{m+i-1 \choose i}={m+n \choose n}}$

${\displaystyle \sum _{i=0}^{n}{n \choose i}^{2}={2n \choose n}}$

${\displaystyle \sum _{i=0}^{n}{\frac {1}{i!}}={\frac {\lfloor n!\;e\rfloor }{n!}}}$

${\displaystyle \sum _{i=1}^{n}{\frac {1}{i}}=H_{n}\quad }$( n- й гармонический номер )

${\displaystyle \sum _{i=1}^{n}{\frac {1}{i^{k}}}=H_{n}^{k}\quad }$( обобщенное гармоническое число )

Ниже приведены полезные приближения (с использованием тета-обозначения ):

${\displaystyle \sum _{i=1}^{n}i^{c}\in \Theta (n^{c+1})}$для вещественного c больше −1

${\displaystyle \sum _{i=1}^{n}{\frac {1}{i}}\in \Theta (\log _{e}n)}$(См. Гармонический номер )

${\displaystyle \sum _{i=1}^{n}c^{i}\in \Theta (c^{n})}$для вещественного c больше 1

${\displaystyle \sum _{i=1}^{n}\log(i)^{c}\in \Theta (n\cdot \log(n)^{c})}$для неотрицательного действительного числа c

${\displaystyle \sum _{i=1}^{n}\log(i)^{c}\cdot i^{d}\in \Theta (n^{d+1}\cdot \log(n)^{c})}$для неотрицательных действительных c , d

${\displaystyle \sum _{i=1}^{n}\log(i)^{c}\cdot i^{d}\cdot b^{i}\in \Theta (n^{d}\cdot \log(n)^{c}\cdot b^{n})}$для неотрицательных действительных b > 1, c , d

• В 1675 году Готфрид Вильгельм Лейбниц в письме Генри Ольденбургу предлагает символ ∫ для обозначения суммы дифференциалов ( лат . calculus summatorius ), отсюда и S-образная форма. ^{[5] [6] [7]} Переименование этого символа в интеграл произошло позже в ходе обмена мнениями с Иоганном Бернулли . ^[7]
• В 1755 году символ суммы Σ был засвидетельствован в труде Леонарда Эйлера « Institutiones calculi Differentis» . ^{[8] [9]} Эйлер использует этот символ в выражениях типа:

${\displaystyle \Sigma \ (2wx+w^{2})=x^{2}}$

• В 1772 году использование Σ и Σ ⁿ засвидетельствовано Лагранжем . ^{[8] [10]}
• В 1823 году заглавная буква S была засвидетельствована как символ суммирования рядов. Такое использование, по-видимому, было широко распространено. ^[8]
• В 1829 году символ суммы Σ был засвидетельствован Фурье и К. Г. Дж. Якоби . ^[8] Использование Фурье включало нижние и верхние границы, например: ^{[11] [12]}

${\displaystyle \sum _{i=1}^{\infty }e^{-i^{2}t}\ldots }$

• Заглавная цифра «пи»
• Обозначение Эйнштейна
• скобка Айверсона
• Итерированная бинарная операция
• Алгоритм суммирования Кахана
• Продукт (математика)
• Суммирование по частям
• Сигма § Кодировка символов

• Каджори, Флориан (1929). История математических обозначений, том II. Open Court Publishing. ISBN 978-0-486-67766-8.

• Медиа, связанные с Summation на Wikimedia Commons