Функция делителя

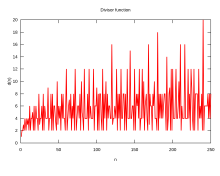
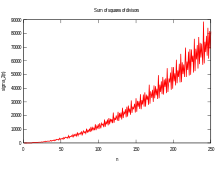
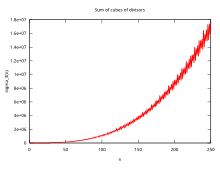
В математике , и в частности в теории чисел , функция делителей — это арифметическая функция, связанная с делителями целого числа . Когда ее называют функцией делителей, она подсчитывает количество делителей целого числа (включая 1 и само число). Она появляется в ряде замечательных тождеств, включая соотношения на дзета-функции Римана и ряд Эйзенштейна модулярных форм . Функции делителей изучались Рамануджаном , который дал ряд важных сравнений и тождеств ; они рассматриваются отдельно в статье Сумма Рамануджана .

Связанной функцией является функция суммирования делителей , которая, как следует из названия, представляет собой сумму по функции делителей.

Сумма положительных делителей функции σ _z ( n ), для действительного или комплексного числа z , определяется как сумма степеней z положительных делителей числа n . Она может быть выражена в сигма - обозначении как

${\displaystyle \sigma _{z}(n)=\sum _{d\mid n}d^{z}\,\!,}$

где — сокращение от « d делит n ». Обозначения d ( n ), ν ( n ) и τ ( n ) (для немецкого Teiler = divisors) также используются для обозначения σ ₀ ( n ) или функции числа делителей ^{[1] [2]} ( OEIS : A000005 ). Когда z равно 1, функция называется сигма-функцией или функцией суммы делителей ^{[1] [3]} и нижний индекс часто опускается, поэтому σ ( n ) совпадает с σ ₁ ( n ) ( OEIS : A000203 ).${\displaystyle {d\mid n}}$

Аликвотная сумма s ( n ) числа n является суммой собственных делителей (то есть делителей, исключая само n , OEIS : A001065 ) и равна σ ₁ ( n ) −  n ; аликвотная последовательность числа n формируется путем многократного применения функции аликвотной суммы.

Например, σ ₀ (12) — число делителей числа 12:

${\displaystyle {\begin{align}\sigma _{0}(12)&=1^{0}+2^{0}+3^{0}+4^{0}+6^{0}+12^{0}\\&=1+1+1+1+1+1=6,\end{align}}}$

в то время как σ ₁ (12) — сумма всех делителей:

${\displaystyle {\begin{align}\sigma _{1}(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}+12^{1}\\&=1+2+3+4+6+12=28,\end{align}}}$

а аликвотная сумма s(12) собственных делителей равна:

${\displaystyle {\begin{align}s(12)&=1^{1}+2^{1}+3^{1}+4^{1}+6^{1}\\&=1+2+3+4+6=16.\end{align}}}$

σ ₋₁ ( n ) иногда называют индексом обилия n , и мы имеем :

${\displaystyle {\begin{aligned}\sigma _{-1}(12)&=1^{-1}+2^{-1}+3^{-1}+4^{-1}+6^{-1}+12^{-1}\\[6pt]&={\tfrac {1}{1}}+{\tfrac {1}{2}}+{\tfrac {1}{3}}+{\tfrac {1}{4}}+{\tfrac {1}{6}}+{\tfrac {1}{12}}\\[6pt]&={\tfrac {12}{12}}+{\tfrac {6}{12}}+{\tfrac {4}{12}}+{\tfrac {3}{12}}+{\tfrac {2}{12}}+{\tfrac {1}{12}}\\[6pt]&={\tfrac {12+6+4+3+2+1}{12}}={\tfrac {28}{12}}={\tfrac {7}{3}}={\tfrac {\sigma _{1}(12)}{12}}\end{выровнено}}}$

Случаи x = от 2 до 5 перечислены в OEIS : A001157 — OEIS : A001160 , x = от 6 до 24 перечислены в OEIS : A013954 — OEIS : A013972 .

Для простого числа p ,

${\displaystyle {\begin{align}\сигма _{0}(p)&=2\\\сигма _{0}(p^{n})&=n+1\\\сигма _{1}(p)&=p+1\end{align}}}$

потому что по определению множители простого числа — это 1 и само число. Кроме того, где p _n # обозначает изначальный элемент ,

${\displaystyle \сигма _{0}(p_{n}\#)=2^{n}}$

поскольку n простых множителей допускают последовательность бинарного выбора ( или 1) из n членов для каждого образованного правильного делителя. Однако, в общем случае, это не наименьшие числа, число делителей которых является степенью двойки ; вместо этого наименьшее такое число может быть получено путем умножения первых n простых чисел Ферми–Дирака , степеней простых чисел, показатель которых является степенью двойки. ^[4]${\displaystyle p_{i}}$

Очевидно, для всех и для всех .${\displaystyle 1<\сигма _{0}(n)<n}$${\displaystyle n>2}$${\displaystyle \сигма _{x}(n)>n}$${\displaystyle n>1}$${\displaystyle х>0}$

Функция делителя является мультипликативной (поскольку каждый делитель c произведения mn по -своему соответствует делителю a числа m и делителю b числа n ), но не полностью мультипликативной :${\displaystyle \НОД(м,п)=1}$

${\displaystyle \gcd(a,b)=1\Longrightarrow \sigma _{x}(ab)=\sigma _{x}(a)\sigma _{x}(b).}$

Следствием этого является то, что если мы напишем

${\displaystyle n=\prod _{i=1}^{r}p_{i}^{a_{i}}}$

где r  =  ω ( n ) — число различных простых множителей числа n , p _i — i- й простой множитель, а a _i — максимальная степень числа p _{i ,} на которую делится n , тогда имеем: ^[5]

${\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}\sum _{j=0}^{a_{i}}p_{i}^{jx}=\prod _{i=1}^{r}\left(1+p_{i}^{x}+p_{i}^{2x}+\cdots +p_{i}^{a_{i}x}\right).}$

что, когда x  ≠ 0, эквивалентно полезной формуле: ^[5]

${\displaystyle \sigma _{x}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{(a_{i}+1)x}-1}{p_{i}^{x}-1}}.}$

Когда x  = 0, это: ^[5]${\displaystyle \sigma _{0}(n)}$

${\displaystyle \sigma _{0}(n)=\prod _{i=1}^{r}(a_{i}+1).}$

Этот результат можно напрямую вывести из того факта, что все делители однозначно определяются различными кортежами целых чисел с (т.е. независимым выбором для каждого ).${\displaystyle n}$${\displaystyle (x_{1},x_{2},...,x_{i},...,x_{r})}$${\displaystyle 0\leq x_{i}\leq a_{i}}$${\displaystyle a_{i}+1}$${\displaystyle x_{i}}$

Например, если n равно 24, то есть два простых множителя ( p ₁ равно 2; p ₂ равно 3); отметим, что 24 является произведением 2 ³ ×3 ¹ , a ₁ равно 3, а a ₂ равно 1. Таким образом, мы можем вычислить следующим образом:${\displaystyle \sigma _{0}(24)}$

${\displaystyle \sigma _{0}(24)=\prod _{i=1}^{2}(a_{i}+1)=(3+1)(1+1)=4\cdot 2=8.}$

Восемь делителей, подсчитываемых по этой формуле, — 1, 2, 4, 8, 3, 6, 12 и 24.

Эйлер доказал замечательную повторяемость: ^{[6] [7] [8]}

${\displaystyle {\begin{aligned}\sigma _{1}(n)&=\sigma _{1}(n-1)+\sigma _{1}(n-2)-\sigma _{1}(n-5)-\sigma _{1}(n-7)+\sigma _{1}(n-12)+\sigma _{1}(n-15)+\cdots \\[12mu]&=\sum _{i\in \mathbb {N} }(-1)^{i+1}\left(\sigma _{1}\left(n-{\frac {1}{2}}\left(3i^{2}-i\right)\right)+\sigma _{1}\left(n-{\frac {1}{2}}\left(3i^{2}+i\right)\right)\right),\end{aligned}}}$

где если это происходит и для , и являются последовательными парами обобщенных пятиугольных чисел ( OEIS : A001318 , начиная со смещения 1). Действительно, Эйлер доказал это логарифмическим дифференцированием тождества в своей теореме о пятиугольных числах .${\displaystyle \sigma _{1}(0)=n}$${\displaystyle \sigma _{1}(x)=0}$${\displaystyle x<0}$${\displaystyle {\tfrac {1}{2}}\left(3i^{2}\mp i\right)}$

Для неквадратного целого числа n каждый делитель d числа n парен делителю n / d числа n и является четным; для квадратного целого числа один делитель (а именно ) не парен отдельному делителю и является нечетным. Аналогично, число является нечетным тогда и только тогда, когда n является квадратом или дважды квадратом. ^[9]${\displaystyle \sigma _{0}(n)}$${\displaystyle {\sqrt {n}}}$${\displaystyle \sigma _{0}(n)}$${\displaystyle \sigma _{1}(n)}$

Отметим также, что s ( n ) = σ ( n ) −  n . Здесь s ( n ) обозначает сумму собственных делителей числа n , то есть делителей числа n , исключая само n . Эта функция используется для распознавания совершенных чисел , то есть таких n , что s ( n ) =  n . Если s ( n ) > n , то n является избыточным числом , а если s ( n ) < n , то n является дефицитным числом .

Если n — степень числа 2 , то и , что делает n почти идеальным .${\displaystyle n=2^{k}}$${\displaystyle \sigma (n)=2\cdot 2^{k}-1=2n-1}$${\displaystyle s(n)=n-1}$

В качестве примера, для двух простых чисел пусть${\displaystyle p,q:p<q}$

${\displaystyle n=p\,q}$.

Затем

${\displaystyle \sigma (n)=(p+1)(q+1)=n+1+(p+q),}$

${\displaystyle \varphi (n)=(p-1)(q-1)=n+1-(p+q),}$

и

${\displaystyle n+1=(\sigma (n)+\varphi (n))/2,}$

${\displaystyle p+q=(\sigma (n)-\varphi (n))/2,}$

где — функция Эйлера .${\displaystyle \varphi (n)}$

Затем корни

${\displaystyle (x-p)(x-q)=x^{2}-(p+q)x+n=x^{2}-[(\sigma (n)-\varphi (n))/2]x+[(\sigma (n)+\varphi (n))/2-1]=0}$

выразить p и q только через σ ( n ) и φ ( n ), не требуя знания n или , как${\displaystyle p+q}$

${\displaystyle p=(\sigma (n)-\varphi (n))/4-{\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\sigma (n)+\varphi (n))/2-1]}},}$

${\displaystyle q=(\sigma (n)-\varphi (n))/4+{\sqrt {[(\sigma (n)-\varphi (n))/4]^{2}-[(\sigma (n)+\varphi (n))/2-1]}}.}$

Кроме того, зная n и либо или , либо , альтернативно, и либо или , можно легко восстановить p и q .${\displaystyle \sigma (n)}$${\displaystyle \varphi (n)}$${\displaystyle p+q}$${\displaystyle \sigma (n)}$${\displaystyle \varphi (n)}$

В 1984 году Роджер Хит-Браун доказал, что равенство

${\displaystyle \sigma _{0}(n)=\sigma _{0}(n+1)}$

верно для бесконечного числа значений n , см. OEIS : A005237 .

По определению: По методу обращения Мёбиуса :$${\displaystyle \sigma =\operatorname {Id} *\mathbf {1} }$$$${\displaystyle \operatorname {Id} =\sigma *\mu }$$

Два ряда Дирихле, включающие функцию делителя: ^[10]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a)\quad {\text{for}}\quad s>1,s>a+1,}$

где — дзета-функция Римана . Ряд для d ( n ) =  σ ₀ ( n ) дает: ^[10]${\displaystyle \zeta }$

${\displaystyle \sum _{n=1}^{\infty }{\frac {d(n)}{n^{s}}}=\zeta ^{2}(s)\quad {\text{for}}\quad s>1,}$

и тождество Рамануджана ^[11]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}},}$

что является частным случаем свертки Ранкина–Сельберга .

Ряд Ламберта , включающий функцию делителя, имеет вид: ^[12]

${\displaystyle \sum _{n=1}^{\infty }q^{n}\sigma _{a}(n)=\sum _{n=1}^{\infty }\sum _{j=1}^{\infty }n^{a}q^{j\,n}=\sum _{n=1}^{\infty }{\frac {n^{a}q^{n}}{1-q^{n}}}}$

для произвольных комплексных | q | ≤ 1 и  a . Это суммирование также появляется как ряд Фурье ряда Эйзенштейна и инварианты эллиптических функций Вейерштрасса .

Для существует явное представление ряда с суммами Рамануджана в виде: ^[13]${\displaystyle k>0}$ ${\displaystyle c_{m}(n)}$

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\sum _{m=1}^{\infty }{\frac {c_{m}(n)}{m^{k+1}}}.}$

Вычисление первых членов показывает их колебания вокруг «среднего значения» :${\displaystyle c_{m}(n)}$${\displaystyle \zeta (k+1)n^{k}}$

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\left[1+{\frac {(-1)^{n}}{2^{k+1}}}+{\frac {2\cos {\frac {2\pi n}{3}}}{3^{k+1}}}+{\frac {2\cos {\frac {\pi n}{2}}}{4^{k+1}}}+\cdots \right]}$

В записи с маленьким о функция делителя удовлетворяет неравенству: ^{[14] [15]}

${\displaystyle {\mbox{for all }}\varepsilon >0,\quad d(n)=o(n^{\varepsilon }).}$

Точнее, Северин Вигерт показал, что: ^[15]

${\displaystyle \limsup _{n\to \infty }{\frac {\log d(n)}{\log n/\log \log n}}=\log 2.}$

С другой стороны, поскольку существует бесконечно много простых чисел , ^[15]

${\displaystyle \liminf _{n\to \infty }d(n)=2.}$

В нотации Big-O Питер Густав Лежен Дирихле показал, что средний порядок функции делителя удовлетворяет следующему неравенству: ^{[16] [17]}

${\displaystyle {\mbox{for all }}x\geq 1,\sum _{n\leq x}d(n)=x\log x+(2\gamma -1)x+O({\sqrt {x}}),}$

где — гамма-константа Эйлера . Улучшение оценки в этой формуле известно как проблема делителей Дирихле .${\displaystyle \gamma }$${\displaystyle O({\sqrt {x}})}$

Поведение сигма-функции нерегулярно. Асимптотическая скорость роста сигма-функции может быть выражена как: ^[18]

${\displaystyle \limsup _{n\rightarrow \infty }{\frac {\sigma (n)}{n\,\log \log n}}=e^{\gamma },}$

где lim sup — верхний предел . Этот результат — теорема Грёнвалля , опубликованная в 1913 году (Grönwall 1913). Его доказательство использует третью теорему Мертенса , которая гласит:

${\displaystyle \lim _{n\to \infty }{\frac {1}{\log n}}\prod _{p\leq n}{\frac {p}{p-1}}=e^{\gamma },}$

где p обозначает простое число.

В 1915 году Рамануджан доказал, что при предположении гипотезы Римана неравенство Робина

${\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n}$(где γ — константа Эйлера–Маскерони )

справедливо для всех достаточно больших n (Ramanujan 1997). Наибольшее известное значение, которое нарушает неравенство, равно n = 5040. В 1984 году Гай Робин доказал, что неравенство верно для всех n > 5040 тогда и только тогда, когда верна гипотеза Римана (Robin 1984). Это теорема Робина , и неравенство стало известно после него. Робин также показал, что если гипотеза Римана ложна, то существует бесконечное число значений n , которые нарушают неравенство, и известно, что наименьшее такое n > 5040 должно быть сверхизбыточным (Akbary & Friggstad 2009). Было показано, что неравенство верно для больших нечетных и свободных от квадратов целых чисел, и что гипотеза Римана эквивалентна неравенству только для n , делящегося на пятую степень простого числа (Choie et al. 2007).

Робин также безоговорочно доказал, что неравенство:

${\displaystyle \ \sigma (n)<e^{\gamma }n\log \log n+{\frac {0.6483\ n}{\log \log n}}}$

справедливо для всех n ≥ 3.

Схожая оценка была дана Джеффри Лагариасом в 2002 году, который доказал, что гипотеза Римана эквивалентна утверждению, что:

${\displaystyle \sigma (n)<H_{n}+e^{H_{n}}\log(H_{n})}$

для каждого натурального числа n > 1, где — n - е гармоническое число , (Лагариас 2002).${\displaystyle H_{n}}$

• Свертки суммы делителей , перечисляет несколько тождеств, включающих функции делителей
• Функция Эйлера тотиент , функция Эйлера фи
• Рефакторинговое число
• Таблица делителей
• Унитарный делитель

• Акбари, Амир; Фриггстад, Закари (2009), «Сверхизобильные числа и гипотеза Римана» (PDF) , American Mathematical Monthly , 116 (3): 273– 275, doi :10.4169/193009709X470128, архивировано из оригинала (PDF) 2014-04-11.
• Апостол, Том М. (1976), Введение в аналитическую теорию чисел , Бакалаврские тексты по математике, Нью-Йорк-Гейдельберг: Springer-Verlag, ISBN 978-0-387-90163-3, MR  0434929, Zbl  0335.10001
• Бах, Эрик ; Шаллит, Джеффри , Алгоритмическая теория чисел , том 1, 1996, MIT Press. ISBN 0-262-02405-5 , см. стр. 234 в разделе 8.8. 
• Кавени, Джеффри; Николя, Жан-Луи ; Сондов, Джонатан (2011), «Теорема Робина, простые числа и новая элементарная переформулировка гипотезы Римана» (PDF) , ЦЕЛЫЕ ЧИСЛА: Электронный журнал комбинаторной теории чисел , 11 : A33, arXiv : 1110.5078 , Bibcode : 2011arXiv1110.5078C
• Чой, ЁнгДжу ; Личиардополь, Николас; Мори, Питер; Соле, Патрик (2007), «О критерии Робина для гипотезы Римана», Journal de théorie des nombres de Bordeaux , 19 (2): 357–372 , arXiv : math.NT/0604314 , doi : 10.5802/jtnb.591, ISSN  1246-7405, МР  2394891, S2CID  3207238, Збл  1163.11059
• Джойя, АА; Вайдья, АM (1967), «Дружественные числа с противоположной четностью», The American Mathematical Monthly , 74 (8): 969–973 , doi :10.2307/2315280, JSTOR  2315280, MR  0220659
• Грёнвалль, Томас Хакон (1913), «Некоторые асимптотические выражения в теории чисел», Труды Американского математического общества , 14 : 113– 122, doi : 10.1090/S0002-9947-1913-1500940-6
• Харди, ГХ ; Райт, ЭМ (2008) [1938], Введение в теорию чисел , пересмотрено Д. Р. Хит-Брауном и Дж. Х. Сильверманом . Предисловие Эндрю Уайлса . (6-е изд.), Оксфорд: Oxford University Press , ISBN 978-0-19-921986-5, MR  2445243, Zbl  1159.11001
• Ивич, Александр (1985), Дзета-функция Римана. Теория дзета-функции Римана с приложениями , A Wiley-Interscience Publication, Нью-Йорк и т. д.: John Wiley & Sons, стр.  385–440 , ISBN 0-471-80634-X, ЗБЛ  0556.10026
• Лагариас, Джеффри К. (2002), «Элементарная задача, эквивалентная гипотезе Римана», The American Mathematical Monthly , 109 (6): 534–543 , arXiv : math/0008177 , doi :10.2307/2695443, ISSN  0002-9890, JSTOR  2695443, MR  1908008, S2CID  15884740
• Лонг, Кэлвин Т. (1972), Элементарное введение в теорию чисел (2-е изд.), Лексингтон: DC Heath and Company , LCCN  77171950
• Петтофреццо, Энтони Дж.; Биркит, Дональд Р. (1970), Элементы теории чисел , Englewood Cliffs: Prentice Hall , LCCN  77081766
• Рамануджан, Шриниваса (1997), «Высокосоставные числа, аннотированные Жаном-Луи Николя и Гаем Робином», The Ramanujan Journal , 1 (2): 119– 153, doi :10.1023/A:1009764017495, ISSN  1382-4090, MR  1606180, S2CID  115619659
• Робин, Гай (1984), «Великие ценности некоторых делителей и гипотез Римана», Journal de Mathématiques Pures et Appliquées , Neuvième Série, 63 (2): 187–213 , ISSN  0021-7824, MR  0774171
• Уильямс, Кеннет С. (2011), Теория чисел в духе Лиувилля , Лондонское математическое общество, студенческие тексты, т. 76, Кембридж: Cambridge University Press , ISBN 978-0-521-17562-3, ЗБЛ  1227.11002

• Вайсштейн, Эрик В. «Функция делителя». MathWorld .
• Вайсштейн, Эрик В. «Теорема Робина». MathWorld .
• Элементарная оценка некоторых сумм сверток, включающих функции делителей PDF статьи Хуарда, Оу, Спирмена и Уильямса. Содержит элементарные (т. е. не опирающиеся на теорию модулярных форм) доказательства сверток сумм делителей, формулы для числа способов представления числа в виде суммы треугольных чисел и связанные с ними результаты.