Пропорционально-интегрально-дифференциальный регулятор
Пропорционально-интегрально-дифференциальный регулятор ( ПИД -регулятор или трехчленный регулятор ) — это механизм управления на основе обратной связи , обычно используемый для управления машинами и процессами, требующими непрерывного управления и автоматической регулировки. Обычно он используется в промышленных системах управления и различных других приложениях, где необходим постоянный контроль посредством модуляции без вмешательства человека. ПИД-регулятор автоматически сравнивает желаемое целевое значение ( уставку или SP) с фактическим значением системы ( переменную процесса или PV). Разница между этими двумя значениями называется значением ошибки , обозначаемым как .
Затем он автоматически применяет корректирующие действия, чтобы привести PV к тому же значению, что и SP, используя три метода: Пропорциональный ( P ) компонент реагирует на текущее значение ошибки, создавая выход , который прямо пропорционален величине ошибки. Это обеспечивает немедленную коррекцию на основе того, насколько далека система от желаемой уставки. Интегральный ( I ) компонент, в свою очередь, учитывает кумулятивную сумму прошлых ошибок, чтобы устранить любые остаточные ошибки установившегося состояния , которые сохраняются с течением времени, устраняя сохраняющиеся несоответствия. Наконец, производный ( D ) компонент предсказывает будущую ошибку, оценивая скорость изменения ошибки, что помогает смягчить перерегулирование и повысить стабильность системы, особенно когда система претерпевает быстрые изменения. ПИД-регулятор снижает вероятность человеческой ошибки и улучшает автоматизацию .
Типичным примером является система круиз-контроля автомобиля . Когда автомобиль сталкивается с холмом, его скорость может снизиться из-за постоянной мощности двигателя. Контроллер ПИД регулирует выходную мощность двигателя, чтобы восстановить желаемую скорость автомобиля, делая это эффективно с минимальной задержкой и перерегулированием.
Теоретическая основа ПИД-регуляторов восходит к началу 1920-х годов с разработкой автоматических систем рулевого управления для судов. Эта концепция была позже принята для автоматического управления процессами в производстве, впервые появившись в пневматических приводах и эволюционировав в электронные контроллеры. ПИД-регуляторы широко используются в многочисленных приложениях, требующих точного, стабильного и оптимизированного автоматического управления , таких как регулирование температуры , управление скоростью двигателя и управление промышленными процессами.
Основная операция

Отличительной особенностью ПИД-регулятора является возможность использования трех членов управления пропорционального, интегрального и производного влияния на выход регулятора для применения точного и оптимального управления. Блок-схема справа показывает принципы того, как эти члены генерируются и применяются. Она показывает ПИД-регулятор, который непрерывно вычисляет значение ошибки как разницу между желаемой уставкой и измеренной переменной процесса : , и применяет коррекцию на основе пропорциональных , интегральных и производных членов. Контроллер пытается минимизировать ошибку с течением времени путем регулировки переменной управления , такой как открытие регулирующего клапана , до нового значения, определяемого взвешенной суммой членов управления.
В этой модели:
- Термин P пропорционален текущему значению ошибки SP − PV . Например, если ошибка велика, выходной сигнал управления будет пропорционально большим при использовании коэффициента усиления "K p ". Использование только пропорционального управления приведет к ошибке между заданным значением и значением процесса, поскольку контроллеру требуется ошибка для генерации пропорционального выходного отклика. В условиях установившегося процесса достигается равновесие с устойчивым "смещением" SP-PV.
- Член I учитывает прошлые значения ошибки SP − PV и интегрирует их с течением времени для получения члена I. Например, если после применения пропорционального управления есть остаточная ошибка SP − PV, интегральный член стремится устранить остаточную ошибку путем добавления эффекта управления из-за исторического кумулятивного значения ошибки. Когда ошибка устранена, интегральный член перестанет расти. Это приведет к уменьшению пропорционального эффекта по мере уменьшения ошибки, но это компенсируется растущим интегральным эффектом.
- Термин D — это наилучшая оценка будущего тренда ошибки SP − PV, основанная на текущей скорости ее изменения. Иногда его называют «упреждающим контролем», поскольку он эффективно стремится уменьшить эффект ошибки SP − PV, оказывая контрольное влияние, создаваемое скоростью изменения ошибки. Чем быстрее изменение, тем больше контрольный или демпфирующий эффект. [1]
Настройка – Баланс этих эффектов достигается настройкой контура для получения оптимальной функции управления. Константы настройки показаны ниже как «K» и должны быть получены для каждого приложения управления, поскольку они зависят от характеристик отклика физической системы, внешней по отношению к контроллеру. Они зависят от поведения измерительного датчика, конечного элемента управления (например, регулирующего клапана), любых задержек сигнала управления и самого процесса. Приблизительные значения констант обычно могут быть изначально введены, зная тип приложения, но они обычно уточняются или настраиваются путем введения изменения уставки и наблюдения за реакцией системы. [2]
Управляющее воздействие – Математическая модель и практический контур выше используют прямое управляющее воздействие для всех членов, что означает, что возрастающая положительная ошибка приводит к возрастающей положительной коррекции выходного управляющего сигнала. Это происходит потому, что термин «ошибка» не является отклонением от заданного значения (фактическое-желаемое), а фактически является необходимой коррекцией (желаемое-фактическое). Система называется обратнодействующей , если необходимо применить отрицательное корректирующее воздействие. Например, если клапан в контуре потока был открыт на 100–0% для управляющего выхода 0–100% – это означает, что действие контроллера должно быть изменено на обратное. Некоторые схемы управления процессами и конечные элементы управления требуют этого обратного действия. Примером может служить клапан для охлаждающей воды, где отказоустойчивый режим в случае потери сигнала будет 100% открытием клапана; поэтому 0% выходного сигнала контроллера должно вызвать 100% открытие клапана.
Математическая форма
Общая функция управления
где , , и , все неотрицательные, обозначают коэффициенты для пропорционального, интегрального и производного членов соответственно (иногда обозначаемые P , I , и D ).
В стандартной форме уравнения (см. далее в статье) и соответственно заменяются на и ; преимущество этого в том, что и имеют некоторый понятный физический смысл, поскольку они представляют собой время интегрирования и время производной соответственно. — постоянная времени, с которой контроллер будет пытаться приблизиться к заданному значению. определяет, как долго контроллер будет допускать, чтобы выходной сигнал постоянно превышал или ниже заданного значения.
Избирательное использование контрольных терминов
Хотя ПИД-регулятор имеет три управляющих члена, некоторым приложениям для обеспечения надлежащего управления достаточно одного или двух членов. Это достигается установкой неиспользуемых параметров на ноль и называется ПИ-, ПД-, П- или И-регулятором при отсутствии других управляющих воздействий. ПИ-регуляторы довольно распространены в приложениях, где производное действие чувствительно к шуму измерения, но интегральный член часто необходим для того, чтобы система достигла своего целевого значения. [ необходима цитата ]
Применимость
Использование алгоритма ПИД не гарантирует оптимального управления системой или ее стабильности управления ( ). Могут возникнуть ситуации, когда имеются чрезмерные задержки: измерение значения процесса задерживается или управляющее воздействие не применяется достаточно быстро. В этих случаях для эффективности требуется компенсация опережения-запаздывания . Реакция контроллера может быть описана с точки зрения его реагирования на ошибку, степени, в которой система превышает заданное значение, и степени любого колебания системы . Но контроллер ПИД широко применим, поскольку он полагается только на реакцию измеренной переменной процесса, а не на знание или модель базового процесса.
История


Происхождение
Непрерывное управление, до того как ПИД-регуляторы были полностью поняты и реализованы, имеет одно из своих истоков в центробежном регуляторе , который использует вращающиеся грузы для управления процессом. Это было изобретено Христианом Гюйгенсом в 17 веке для регулирования зазора между жерновами ветряных мельниц в зависимости от скорости вращения и, таким образом, компенсации переменной скорости подачи зерна. [3] [4]
С изобретением стационарного парового двигателя низкого давления возникла необходимость в автоматическом регулировании скорости, и разработанный Джеймсом Уаттом регулятор « конического маятника », набор вращающихся стальных шариков, прикрепленных к вертикальному шпинделю с помощью рычагов, стал промышленным стандартом. Он был основан на концепции управления зазором жернова. [5]
Однако управление скоростью вращающегося регулятора все еще оставалось переменным в условиях изменяющейся нагрузки, где недостаток того, что сейчас известно как пропорциональное управление, был очевиден. Ошибка между желаемой скоростью и фактической скоростью увеличивалась с увеличением нагрузки. В 19 веке теоретическая основа работы регуляторов была впервые описана Джеймсом Клерком Максвеллом в 1868 году в его ныне знаменитой статье «О регуляторах» . Он исследовал математическую основу устойчивости управления и продвинулся на пути к решению, но обратился к математикам с призывом изучить проблему. [6] [5] Проблема была дополнительно изучена в 1874 году Эдвардом Раутом , Чарльзом Штурмом и в 1895 году Адольфом Гурвицем , каждый из которых внес свой вклад в установление критериев устойчивости управления. [5] В последующих приложениях регуляторы скорости были дополнительно усовершенствованы, в частности, американским ученым Уиллардом Гиббсом , который в 1872 году теоретически проанализировал конический маятниковый регулятор Уатта.
Примерно в это же время изобретение торпеды Уайтхеда поставило проблему управления, которая требовала точного контроля глубины хода. Использование одного только датчика давления глубины оказалось недостаточным, и маятник, измерявший передний и задний наклон торпеды, был объединен с измерением глубины, чтобы стать маятниково-гидростатным управлением . Управление давлением обеспечивало только пропорциональное управление, которое, если усиление управления было слишком высоким, становилось нестабильным и выходило за пределы со значительной нестабильностью удержания глубины. Маятник добавлял то, что сейчас известно как производное управление, которое гасило колебания, определяя угол погружения/подъема торпеды и, таким образом, скорость изменения глубины. [7] Эта разработка (названная Уайтхедом «Секретом», чтобы не давать подсказки о ее действии) была около 1868 года. [8]
Еще один ранний пример регулятора ПИД-типа был разработан Элмером Сперри в 1911 году для управления судном, хотя его работа была скорее интуитивной, чем математически обоснованной. [9]
Однако только в 1922 году формальный закон управления для того, что мы сейчас называем ПИД или трехчленным управлением, был впервые разработан с использованием теоретического анализа русско-американским инженером Николасом Минорским . [10] Минорский исследовал и проектировал автоматическое управление судном для ВМС США и основывал свой анализ на наблюдениях за рулевым . Он отметил, что рулевой управляет судном, основываясь не только на текущей ошибке курса, но и на прошлой ошибке, а также на текущей скорости изменения; [11] затем это было математически обработано Минорским. [5] Его целью была устойчивость, а не общее управление, что значительно упростило задачу. Хотя пропорциональное управление обеспечивало устойчивость против небольших возмущений, его было недостаточно для борьбы с устойчивым возмущением, в частности, с сильным штормом (из-за устойчивой ошибки), что требовало добавления интегрального члена. Наконец, был добавлен производный член для улучшения устойчивости и управления.
Испытания проводились на USS New Mexico , где контроллеры управляли угловой скоростью (а не углом) руля. ПИ-управление дало устойчивое рыскание (угловую ошибку) ±2°. Добавление элемента D дало ошибку рыскания ±1/6°, что лучше, чем могли достичь большинство рулевых. [12]
В конечном итоге ВМС не приняли систему из-за сопротивления персонала. Подобная работа была проведена и опубликована несколькими другими [ кто? ] в 1930-х годах. [ нужна цитата ]
Промышленный контроль
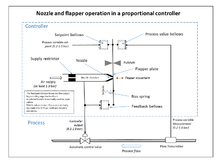
Широкое использование контроллеров обратной связи не стало возможным до разработки широкополосных усилителей с высоким коэффициентом усиления для использования концепции отрицательной обратной связи . Это было разработано в телефонной инженерной электронике Гарольдом Блэком в конце 1920-х годов, но не опубликовано до 1934 года. [5] Независимо от этого, Клессон Э. Мейсон из компании Foxboro в 1930 году изобрел широкополосный пневматический контроллер, объединив пневматический усилитель с высоким коэффициентом усиления сопла и заслонки , который был изобретен в 1914 году, с отрицательной обратной связью от выхода контроллера. Это значительно увеличило линейный диапазон работы усилителя сопла и заслонки, а интегральное управление также могло быть добавлено с помощью прецизионного выпускного клапана и сильфона, генерирующего интегральный член. Результатом стал контроллер «Stabilog», который давал как пропорциональные, так и интегральные функции с использованием сильфонов обратной связи. [5] Интегральный член был назван Reset . [13] Позже производный член был добавлен дополнительным сильфоном и регулируемым отверстием.
Начиная примерно с 1932 года, широкополосные пневматические контроллеры стали быстро использоваться в различных приложениях управления. Давление воздуха использовалось для генерации выходного сигнала контроллера, а также для питания устройств модуляции процесса, таких как регулирующие клапаны с мембранным приводом. Это были простые устройства с низкими требованиями к обслуживанию, которые хорошо работали в суровых промышленных условиях и не представляли опасности взрыва в опасных местах . Они были отраслевым стандартом в течение многих десятилетий до появления дискретных электронных контроллеров и распределенных систем управления (DCS).
С помощью этих контроллеров был установлен стандарт пневматической сигнализации в 3–15 фунтов на квадратный дюйм (0,2–1,0 бар), который имел повышенный ноль, чтобы гарантировать работу устройств в пределах их линейной характеристики и представлял диапазон управления 0–100%.
В 1950-х годах, когда электронные усилители с высоким коэффициентом усиления стали дешевыми и надежными, электронные ПИД-регуляторы стали популярными, а пневматический стандарт был эмулирован сигналами токовой петли 10-50 мА и 4-20 мА (последний стал отраслевым стандартом). Пневматические полевые приводы по-прежнему широко используются из-за преимуществ пневматической энергии для регулирующих клапанов в условиях технологических установок.
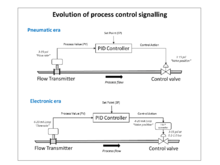
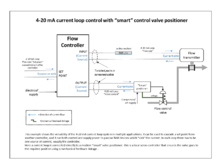
Большинство современных ПИД-регуляторов в промышленности реализованы в виде компьютерного программного обеспечения в РСУ, программируемых логических контроллерах (ПЛК) или дискретных компактных контроллерах .
Электронные аналоговые контроллеры
Электронные аналоговые контуры ПИД-регулирования часто встречаются в более сложных электронных системах, например, позиционирование головки дисковода , кондиционирование питания источника питания или даже схема обнаружения движения современного сейсмометра . Дискретные электронные аналоговые контроллеры были в значительной степени заменены цифровыми контроллерами, использующими микроконтроллеры или ПЛИС для реализации алгоритмов ПИД. Однако дискретные аналоговые ПИД-контроллеры все еще используются в нишевых приложениях, требующих высокой пропускной способности и низкого уровня шума, таких как контроллеры лазерных диодов. [14]
Пример контура управления
Рассмотрим роботизированную руку [15], которая может перемещаться и позиционироваться с помощью контура управления. Электродвигатель может поднимать или опускать руку в зависимости от приложенной прямой или обратной мощности, но мощность не может быть простой функцией положения из-за инерционной массы руки, сил, вызванных гравитацией, внешних сил на руке, таких как груз для подъема или работа, которую нужно выполнить над внешним объектом.
- Измеренное положение является переменной процесса (PV).
- Требуемое положение называется уставкой (УП).
- Разница между PV и SP — это ошибка (e), которая количественно определяет, находится ли рычаг слишком низко или слишком высоко, и насколько.
- Входом в процесс ( электрический ток в двигателе) является выход ПИД-регулятора. Он называется либо управляемой переменной (MV), либо управляющей переменной (CV).
Измеряя положение (PV) и вычитая его из уставки (SP), можно найти ошибку (e), на основе которой контроллер вычисляет величину электрического тока, подаваемого на двигатель (MV).
Пропорциональный
Очевидный метод — пропорциональное управление: ток двигателя устанавливается пропорционально существующей ошибке. Однако этот метод не работает, если, например, рука должна поднимать разные веса: больший вес требует большей силы, приложенной для той же ошибки на нижней стороне, но меньшей силы, если ошибка низкая на верхней стороне. Вот где играют свою роль интегральные и производные члены.
Интеграл
Интегральный член увеличивает действие не только по отношению к ошибке, но и ко времени, в течение которого она сохраняется. Таким образом, если приложенной силы недостаточно, чтобы свести ошибку к нулю, эта сила будет увеличиваться с течением времени. Чистый «I»-контроллер мог бы свести ошибку к нулю, но он будет как слабо реагировать в начале (потому что действие будет небольшим в начале, в зависимости от времени, чтобы стать значительным), так и более агрессивно в конце (действие увеличивается, пока ошибка положительна, даже если ошибка близка к нулю).
Применение слишком большого интеграла, когда ошибка мала и уменьшается, приведет к перерегулированию. Если после перерегулирования контроллер применит большую коррекцию в противоположном направлении и многократно перерегулирует желаемое положение, выход будет колебаться вокруг заданного значения либо по постоянной, либо по растущей, либо по затухающей синусоиде . Если амплитуда колебаний увеличивается со временем, система нестабильна. Если она уменьшается, система стабильна. Если колебания остаются на постоянной величине, система является минимально стабильной .
Производный
Производный член не учитывает величину ошибки (то есть не может свести ее к нулю: чистый D-контроллер не может привести систему к заданному значению), а скорее скорость изменения ошибки, пытаясь свести эту скорость к нулю. Он направлен на выравнивание траектории ошибки в горизонтальную линию, гасит приложенную силу и, таким образом, уменьшает перерегулирование (ошибку с другой стороны из-за слишком большой приложенной силы).
Управление демпфированием
В интересах достижения контролируемого прибытия в желаемое положение (SP) своевременно и точно, контролируемая система должна быть критически демпфирована . Хорошо настроенная система управления положением также будет подавать необходимые токи на управляемый двигатель, чтобы рука толкала и тянула по мере необходимости, чтобы противостоять внешним силам, пытающимся сместить ее из требуемого положения. Сама уставка может быть сгенерирована внешней системой, такой как ПЛК или другая компьютерная система, так что она непрерывно меняется в зависимости от работы, которую, как ожидается, будет выполнять роботизированная рука. Хорошо настроенная система управления ПИД позволит руке соответствовать этим изменяющимся требованиям в меру своих возможностей.
Реакция на нарушения
Если контроллер запускается из стабильного состояния с нулевой ошибкой (PV = SP), то дальнейшие изменения контроллера будут в ответ на изменения других измеренных или неизмеренных входов процесса, которые влияют на процесс, и, следовательно, на PV. Переменные, которые влияют на процесс, отличные от MV, известны как возмущения. Обычно контроллеры используются для отклонения возмущений и для реализации изменений заданных значений. Изменение нагрузки на руку представляет собой возмущение процесса управления рукой робота.
Приложения
Теоретически контроллер может использоваться для управления любым процессом, имеющим измеримый выход (PV), известное идеальное значение для этого выхода (SP) и вход в процесс (MV), который будет влиять на соответствующий PV. Контроллеры используются в промышленности для регулирования температуры , давления , силы , скорости подачи , [16] расхода , химического состава ( концентрации компонентов ), веса , положения , скорости и практически любой другой переменной, для которой существует измерение.
Теория контроллера
- В этом разделе описывается параллельная или невзаимодействующая форма ПИД-регулятора. Для других форм см. § Альтернативная номенклатура и формы.
Схема ПИД-регулирования названа в честь трех ее корректирующих членов, сумма которых составляет управляемую переменную (MV). Пропорциональные, интегральные и производные члены суммируются для расчета выходного сигнала ПИД-регулятора. Определяя как выходной сигнал регулятора, окончательная форма алгоритма ПИД-регулирования имеет вид
где
- это пропорциональный коэффициент усиления, параметр настройки,
- - интегральный коэффициент усиления, параметр настройки,
- это производный коэффициент усиления, параметр настройки,
- — ошибка (SP — уставка, а PV( t ) — переменная процесса),
- это время или мгновенное время (настоящее),
- — переменная интегрирования (принимает значения от момента времени 0 до настоящего момента ).
Эквивалентно, передаточная функция в области Лапласа ПИД-регулятора имеет вид
где - комплексная частота.
Пропорциональный член

Пропорциональный член создает выходное значение, пропорциональное текущему значению ошибки. Пропорциональный ответ можно скорректировать, умножив ошибку на константу K p , называемую константой пропорционального усиления.
Пропорциональный член определяется выражением
Высокий пропорциональный коэффициент усиления приводит к большому изменению выходного сигнала при заданном изменении ошибки. Если пропорциональный коэффициент усиления слишком высок, система может стать нестабильной (см. раздел о настройке контура). Напротив, малый коэффициент усиления приводит к малому выходному отклику на большую входную ошибку и менее отзывчивому или менее чувствительному контроллеру. Если пропорциональный коэффициент усиления слишком низок, управляющее воздействие может быть слишком малым при реагировании на системные возмущения. Теория настройки и промышленная практика показывают, что пропорциональный член должен вносить большую часть изменения выходного сигнала. [ необходима цитата ]
Ошибка устойчивого состояния
Установившаяся ошибка — это разница между желаемым конечным выходом и фактическим. [17] Поскольку для его управления требуется ненулевая ошибка, пропорциональный контроллер обычно работает с установившейся ошибкой. [a] Установившаяся ошибка (SSE) пропорциональна коэффициенту усиления процесса и обратно пропорциональна пропорциональному коэффициенту усиления. SSE можно смягчить, добавив компенсирующий член смещения к заданному значению и выходу или скорректировать динамически, добавив интегральный член.
Интегральный член
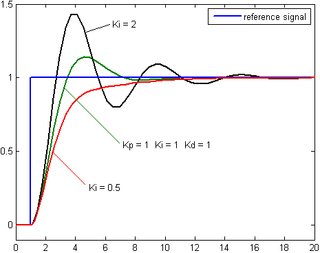
Вклад интегрального члена пропорционален как величине ошибки, так и длительности ошибки. Интеграл в ПИД-регуляторе представляет собой сумму мгновенной ошибки по времени и дает накопленное смещение, которое должно было быть исправлено ранее. Затем накопленная ошибка умножается на интегральный коэффициент усиления ( K i ) и добавляется к выходу контроллера.
Интегральный член определяется выражением
Интегральный член ускоряет движение процесса к заданному значению и устраняет остаточную погрешность установившегося состояния, которая возникает при использовании чистого пропорционального регулятора. Однако, поскольку интегральный член реагирует на накопленные ошибки из прошлого, он может привести к тому, что текущее значение превысит заданное значение (см. раздел о настройке контура).
Производный термин
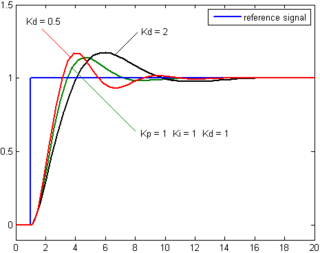
Производная погрешности процесса вычисляется путем определения наклона погрешности во времени и умножения этой скорости изменения на производный коэффициент усиления K d . Величина вклада производного члена в общее управляющее воздействие называется производным коэффициентом усиления, K d .
Производный член определяется как
Производное действие предсказывает поведение системы и, таким образом, улучшает время установления и стабильность системы. [18] [19] Идеальная производная не является причинной , поэтому реализации ПИД-регуляторов включают дополнительную фильтрацию нижних частот для производного члена, чтобы ограничить высокочастотное усиление и шум. Однако производное действие редко используется на практике — по одной из оценок, всего в 25% развернутых контроллеров [ необходима ссылка ] — из-за его переменного влияния на стабильность системы в реальных приложениях.
Настройка петли
Настройка контура управления — это настройка его параметров управления (пропорциональный диапазон/усиление, интегральный коэффициент/сброс, производный коэффициент/скорость) до оптимальных значений для желаемого ответа управления. Устойчивость (отсутствие неограниченных колебаний) является основным требованием, но помимо этого разные системы ведут себя по-разному, разные приложения предъявляют разные требования, и требования могут конфликтовать друг с другом.
Несмотря на то, что есть только три параметра и это просто описать в принципе, настройка ПИД является сложной проблемой, поскольку она должна удовлетворять сложным критериям в рамках ограничений ПИД-регулирования. Соответственно, существуют различные методы настройки контура, а более сложные методы являются предметом патентов; в этом разделе описываются некоторые традиционные ручные методы настройки контура.
Проектирование и настройка ПИД-регулятора кажутся концептуально интуитивными, но на практике могут быть сложными, если необходимо достичь нескольких (и часто противоречивых) целей, таких как короткий переходный процесс и высокая стабильность. ПИД-регуляторы часто обеспечивают приемлемое управление с использованием настроек по умолчанию, но производительность, как правило, можно улучшить путем тщательной настройки, а производительность может быть неприемлемой при плохой настройке. Обычно первоначальные проекты необходимо многократно корректировать с помощью компьютерного моделирования, пока замкнутая система не будет работать или идти на компромиссы так, как требуется.
Некоторые процессы имеют степень нелинейности , поэтому параметры, которые хорошо работают в условиях полной нагрузки, не работают, когда процесс запускается без нагрузки. Это можно исправить с помощью планирования усиления (использование различных параметров в различных рабочих областях).
Стабильность
Если параметры ПИД-регулятора (коэффициенты усиления пропорционального, интегрального и производного членов) выбраны неправильно, управляемый вход процесса может быть нестабильным; т. е. его выход расходится , с колебаниями или без них , и ограничивается только насыщением или механическим поломкой. Нестабильность вызывается избыточным усилением, особенно при наличии значительного запаздывания.
Как правило, требуется стабилизация реакции, и процесс не должен колебаться при любой комбинации условий процесса и уставок, хотя иногда допустима или желательна предельная устойчивость (ограниченные колебания). [ необходима ссылка ]
Математически истоки неустойчивости можно увидеть в области Лапласа . [20]
Передаточная функция замкнутого контура имеет вид
где — передаточная функция ПИД, а — передаточная функция объекта. Система нестабильна , когда передаточная функция замкнутого контура расходится для некоторого . [20] Это происходит в ситуациях, когда . Другими словами, это происходит, когда со сдвигом фаз на 180°. Устойчивость гарантируется, когда для частот, которые испытывают большие сдвиги фаз. Более общий формализм этого эффекта известен как критерий устойчивости Найквиста .
Оптимальное поведение
Оптимальное поведение при изменении процесса или заданного значения зависит от области применения.
Два основных требования — это регулирование (подавление помех — поддержание заданного значения) и отслеживание команд (реализация изменений заданного значения). Эти термины относятся к тому, насколько хорошо контролируемая переменная отслеживает желаемое значение. Конкретные критерии для отслеживания команд включают время нарастания и время установления . Некоторые процессы не должны допускать превышения переменной процесса за пределы заданного значения, если, например, это было бы небезопасно. Другие процессы должны минимизировать затраты энергии на достижение нового заданного значения.
Обзор методов настройки
Существует несколько методов настройки контура ПИД. Наиболее эффективные методы обычно включают разработку некоторой формы модели процесса и последующий выбор P, I и D на основе параметров динамической модели. Методы ручной настройки могут быть относительно трудоемкими, особенно для систем с большим временем цикла.
Выбор метода во многом зависит от того, можно ли отключить контур для настройки, а также от времени отклика системы. Если систему можно отключить, наилучший метод настройки часто включает в себя подвергание системы ступенчатому изменению входного сигнала, измерение выходного сигнала как функции времени и использование этого отклика для определения параметров управления. [ необходима цитата ]
| Метод | Преимущества | Недостатки |
|---|---|---|
| Ручная настройка | Математика не требуется; онлайн. | Это итеративная, основанная на опыте, пробная и ошибочная процедура, которая может быть относительно трудоемкой. Операторы могут обнаружить «плохие» параметры без надлежащего обучения. [21] |
| Циглер–Николс | Онлайн-настройка без каких-либо параметров настройки, поэтому проста в использовании. | Процесс может нарушаться при настройке, может давать очень агрессивные параметры. Не работает хорошо с процессами с задержкой по времени. [ необходима цитата ] |
| Тиреус Луйбен | Онлайн-настройка — это расширение метода Циглера–Николса, которое, как правило, менее агрессивно. | При настройке могут возникнуть сбои в процессе; оператору необходимо выбрать параметр для метода, требующий понимания. |
| Программные инструменты | Последовательная настройка; онлайн или офлайн — может использовать методы проектирования автоматизированных систем управления ( CAutoD ); может включать анализ клапанов и датчиков; позволяет выполнять моделирование перед загрузкой; может поддерживать настройку в нестационарном состоянии (NSS). | «Настройка черного ящика», требующая указания цели, описывающей оптимальное поведение. |
| Коэн–Кун | Хорошие модели процессов [ необходима ссылка ] . | Офлайн; подходит только для процессов первого порядка. [ необходима цитата ] |
| Острём-Хегглунд | В отличие от метода Циглера–Николса, это не приведет к риску нестабильности контура. Требуется мало предварительных знаний о процессе. [22] | Может давать чрезмерное производное действие и вялый ответ. Более поздние расширения решают эти проблемы, но требуют более сложной процедуры настройки. [22] |
| Простое правило управления (SIMC) | Аналитически получено, работает на процессах с задержкой по времени, имеет дополнительный параметр настройки, который обеспечивает дополнительную гибкость. Настройка может быть выполнена с помощью модели с пошаговым откликом. [21] | Оффлайн метод; не может быть применен к колебательным процессам. Оператор должен выбрать дополнительный параметр настройки. [21] |
Ручная настройка
Если система должна оставаться в сети, один из методов настройки — сначала установить значения и на ноль. Увеличивайте до тех пор, пока выходной сигнал контура не начнет колебаться; затем установите примерно половину этого значения для ответа типа «затухание четверти амплитуды». Затем увеличивайте до тех пор, пока любое смещение не будет исправлено за достаточное время для процесса, но не до тех пор, пока слишком большое значение не вызовет нестабильность. Наконец, увеличивайте , если требуется, до тех пор, пока контур не станет приемлемо быстрым для достижения своего опорного значения после возмущения нагрузки. Слишком большое значение вызывает чрезмерный отклик и перерегулирование. Быстрая настройка контура ПИД обычно немного перерегулирована, чтобы быстрее достичь заданного значения; однако некоторые системы не могут принять перерегулирование, в этом случае требуется чрезмерно затухающая система с замкнутым контуром, которая, в свою очередь, требует настройки, значительно меньшей половины настройки , вызывающей колебания. [ необходима цитата ]
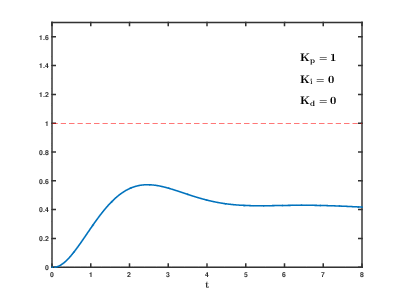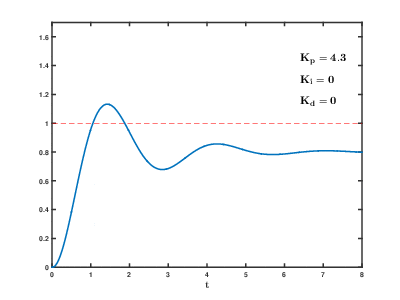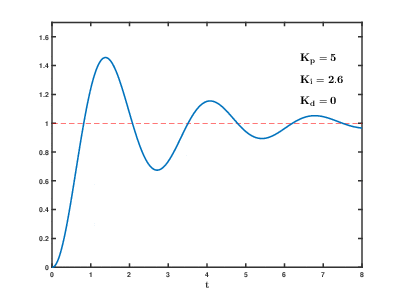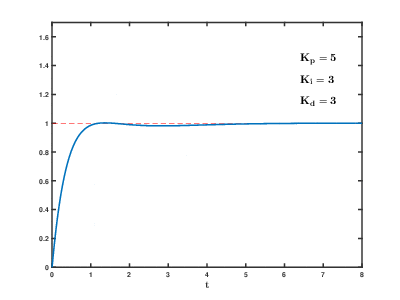
| Параметр | Время подъема | Перелет | Время установления | Ошибка устойчивого состояния | Стабильность |
|---|---|---|---|---|---|
| Снижаться | Увеличивать | Небольшое изменение | Снижаться | Деградировать | |
| Снижаться | Увеличивать | Увеличивать | Устранять | Деградировать | |
| Незначительное изменение | Снижаться | Снижаться | Теоретически никакого эффекта | Улучшить, если маленький |
Метод Циглера–Николса
Другой эвристический метод настройки известен как метод Циглера–Николса , введенный Джоном Г. Циглером и Натаниэлем Б. Николсом в 1940-х годах. Как и в методе выше, коэффициенты усиления и сначала устанавливаются равными нулю. Пропорциональный коэффициент усиления увеличивается до тех пор, пока не достигнет предельного коэффициента усиления, при котором выходной сигнал контура начинает постоянно колебаться. и период колебания используются для установки коэффициентов усиления следующим образом:
| Тип управления | |||
|---|---|---|---|
| П | — | — | |
| ПИ | — | ||
| ПИД |
Вместо этого часто измеряют частоту колебаний, и обратные величины каждого умножения дают тот же результат.
Эти коэффициенты усиления применяются к идеальной, параллельной форме ПИД-регулятора. При применении к стандартной форме ПИД-регулятора только интегральные и производные коэффициенты усиления и зависят от периода колебаний .
Параметры Коэна–Куна
Этот метод был разработан в 1953 году и основан на модели первого порядка + временной задержки. Подобно методу Циглера–Николса , был разработан набор параметров настройки для получения отклика замкнутого контура с коэффициентом затухания . Вероятно, самая большая проблема с этими параметрами заключается в том, что небольшое изменение параметров процесса может потенциально привести к тому, что замкнутая система станет нестабильной.
Релейный метод (Острема – Хэгглунда)
Опубликованный в 1984 году Карлом Йоханом Острёмом и Торе Хэгглундом, [25] релейный метод временно управляет процессом с помощью релейного управления и измеряет результирующие колебания. Выход переключается (как будто с помощью реле , отсюда и название) между двумя значениями управляющей переменной. Значения должны быть выбраны так, чтобы процесс пересекал заданное значение, но они не обязательно должны быть 0% и 100%; выбрав подходящие значения, можно избежать опасных колебаний.
Пока переменная процесса ниже заданного значения, выход управления устанавливается на более высокое значение. Как только он поднимается выше заданного значения, выход управления устанавливается на более низкое значение. В идеале выходная форма волны близка к квадратной, проводя одинаковое время выше и ниже заданного значения. Период и амплитуда результирующих колебаний измеряются и используются для вычисления конечного усиления и периода, которые затем вводятся в метод Циглера–Николса.
В частности, предполагается, что конечный период равен наблюдаемому периоду, а конечный коэффициент усиления вычисляется как, где a — амплитуда колебания переменной процесса, а b — амплитуда изменения выходного сигнала управления, вызвавшего его.
Существует множество вариантов метода реле. [26]
Модель первого порядка с мертвым временем
Передаточная функция для процесса первого порядка с мертвым временем равна
где k p — коэффициент усиления процесса, τ p — постоянная времени, θ — мертвое время, а u ( s ) — входной сигнал с ступенчатым изменением. Преобразование этой передаточной функции во временную область приводит к
используя те же параметры, что и выше.
При использовании этого метода важно применять достаточно большой входной сигнал с ступенчатым изменением, чтобы можно было измерить выходной сигнал; однако слишком большой шаг изменения может повлиять на стабильность процесса. Кроме того, больший шаг изменения гарантирует, что выходной сигнал не изменится из-за помех (для достижения наилучших результатов постарайтесь минимизировать помехи при выполнении шагового теста).
Одним из способов определения параметров для процесса первого порядка является использование метода 63,2%. В этом методе коэффициент усиления процесса ( k p ) равен изменению выхода, деленному на изменение входа. Мертвое время θ — это количество времени между моментом, когда произошло ступенчатое изменение, и моментом, когда выход впервые изменился. Постоянная времени ( τ p ) — это количество времени, которое требуется выходу, чтобы достичь 63,2% от нового стационарного значения после ступенчатого изменения. Одним из недостатков использования этого метода является то, что может потребоваться некоторое время, чтобы достичь нового стационарного значения, если процесс имеет большие временные константы. [27]
Программное обеспечение для настройки
Большинство современных промышленных предприятий больше не настраивают контуры, используя ручные методы расчета, показанные выше. Вместо этого для обеспечения согласованных результатов используется программное обеспечение для настройки ПИД и оптимизации контуров. Эти программные пакеты собирают данные, разрабатывают модели процессов и предлагают оптимальную настройку. Некоторые программные пакеты могут даже разрабатывать настройку, собирая данные из эталонных изменений.
Математическая настройка контура ПИД вызывает импульс в системе, а затем использует частотную характеристику контролируемой системы для проектирования значений контура ПИД. В контурах со временем отклика в несколько минут рекомендуется математическая настройка контура, поскольку пробы и ошибки могут занять дни только для того, чтобы найти стабильный набор значений контура. Оптимальные значения найти сложнее. Некоторые цифровые контроллеры контура предлагают функцию самонастройки, при которой очень небольшие изменения заданного значения отправляются в процесс, что позволяет контроллеру самому вычислять оптимальные значения настройки.
Другой подход вычисляет начальные значения с помощью метода Циглера-Николса и использует технику численной оптимизации для поиска лучших коэффициентов ПИД. [28]
Другие формулы доступны для настройки контура в соответствии с различными критериями производительности. Многие запатентованные формулы теперь встроены в программное обеспечение настройки ПИД и аппаратные модули. [29]
Достижения в области автоматизированного программного обеспечения для настройки контура ПИД также предоставляют алгоритмы для настройки контуров ПИД в динамическом или нестационарном сценарии (NSS). Программное обеспечение моделирует динамику процесса через возмущение и вычисляет параметры управления ПИД в ответ. [30]
Ограничения
Хотя ПИД-регуляторы применимы ко многим проблемам управления и часто работают удовлетворительно без каких-либо улучшений или только грубой настройки, они могут работать плохо в некоторых приложениях и в целом не обеспечивать оптимального управления . Основная трудность ПИД-регулирования заключается в том, что это система управления с обратной связью, с постоянными параметрами и без прямого знания процесса, и, таким образом, общая производительность является реактивной и компромиссной. Хотя ПИД-регулирование является лучшим регулятором для наблюдателя без модели процесса, лучшую производительность можно получить путем открытого моделирования действующего лица процесса, не прибегая к наблюдателю.
Контроллеры PID, используемые в одиночку, могут давать плохую производительность, когда коэффициенты усиления контура PID должны быть уменьшены, чтобы система управления не перерегулирована, не колебалась и не рыскала вокруг значения контрольной уставки. Они также испытывают трудности при наличии нелинейностей, могут идти на компромисс между регулированием и временем отклика, не реагировать на изменение поведения процесса (например, процесс изменяется после того, как он прогрелся) и имеют задержку в реагировании на большие возмущения.
Наиболее значительным улучшением является включение управления прямой связью со знанием о системе и использование ПИД только для управления ошибкой. В качестве альтернативы ПИД можно модифицировать более незначительными способами, например, изменяя параметры (либо планирование усиления в различных вариантах использования, либо адаптивно изменяя их на основе производительности), улучшая измерение (более высокая частота дискретизации, точность и достоверность, а также фильтрация нижних частот при необходимости) или каскадируя несколько ПИД-регуляторов.
Линейность и симметрия
ПИД-регуляторы работают лучше всего, когда контур управления линейный и симметричный. Таким образом, их производительность в нелинейных и асимметричных системах ухудшается.
Нелинейный клапан, например, в приложении управления потоком, приведет к переменной чувствительности контура, требующей демпфирующего действия для предотвращения нестабильности. Одним из решений является использование нелинейной характеристики клапана в алгоритме управления для компенсации этого.
Например, асимметричным применением является регулирование температуры в системах HVAC, использующих только активный нагрев (через нагревательный элемент), где доступно только пассивное охлаждение. Когда требуется снизить контролируемую температуру, выход нагрева отключается, но активного охлаждения нет из-за управляющего выхода. Поэтому любое превышение повышения температуры может быть исправлено только медленно; его нельзя принудительно снизить с помощью управляющего выхода. В этом случае ПИД-регулятор можно настроить на чрезмерное затухание, чтобы предотвратить или уменьшить превышение, но это снижает производительность за счет увеличения времени установления повышения температуры до заданного значения. Присущее этому ухудшение качества управления может быть решено применением активного охлаждения.
Шум в производном выражении
Проблема с производным членом заключается в том, что он усиливает измерение более высокой частоты или шум процесса , что может вызвать большие изменения в выходных данных. Часто бывает полезно отфильтровать измерения с помощью фильтра нижних частот , чтобы удалить компоненты шума более высокой частоты. Поскольку фильтр нижних частот и управление производной могут компенсировать друг друга, объем фильтрации ограничен. Поэтому может быть важна малошумящая аппаратура. Может использоваться нелинейный медианный фильтр , который повышает эффективность фильтрации и практическую производительность. [31] В некоторых случаях дифференциальный диапазон можно отключить с небольшой потерей управления. Это эквивалентно использованию ПИД-регулятора в качестве ПИ-регулятора.
Изменения в алгоритме
Базовый алгоритм ПИД создает некоторые проблемы в приложениях управления, которые были устранены путем внесения незначительных изменений в форму ПИД.
Интегральная намотка
Одной из распространенных проблем, возникающих в результате идеальных реализаций ПИД, является интегральное накручивание . После большого изменения уставки интегральный член может накапливать ошибку, превышающую максимальное значение для переменной регулирования (накручивание), таким образом, система перескакивает и продолжает увеличиваться до тех пор, пока эта накопленная ошибка не будет устранена. Эту проблему можно решить следующим образом:
- Отключение интеграции до тех пор, пока фотоэлектрический модуль не войдет в контролируемую область
- Предотвращение накопления интегрального члена выше или ниже заранее определенных границ
- Обратный расчет интегрального члена для ограничения выходного сигнала регулятора в допустимых пределах. [32]
Выход за пределы известных возмущений
Например, контур ПИД используется для управления температурой электропечи сопротивления, где система стабилизировалась. Теперь, когда дверь открывается и в печь помещается что-то холодное, температура падает ниже заданного значения. Интегральная функция контроллера стремится компенсировать ошибку, вводя другую ошибку в положительном направлении. Этого перерегулирования можно избежать, заморозив интегральную функцию после открытия двери на время, которое обычно требуется контуру управления для повторного нагрева печи.
ПИ-контроллер

ПИ -регулятор (пропорционально-интегральный регулятор) — это частный случай ПИД-регулятора, в котором производная (D) ошибки не используется.
Выход контроллера определяется как
где — погрешность или отклонение фактического измеренного значения ( PV ) от заданного значения ( SP ).
ПИ-регулятор можно легко смоделировать в программном обеспечении, таком как Simulink или Xcos, используя блок «блок-схемы» с операторами Лапласа :
где
- = пропорциональное усиление
- = интегральный коэффициент усиления
Установка значения часто является компромиссом между уменьшением перерегулирования и увеличением времени установления.
Отсутствие производного действия может сделать систему более устойчивой в устойчивом состоянии в случае зашумленных данных. Это происходит потому, что производное действие более чувствительно к высокочастотным термам на входах.
Без производного действия система с ПИ-регулированием менее чувствительна к реальным (не шумовым) и относительно быстрым изменениям состояния, поэтому система будет медленнее достигать заданного значения и медленнее реагировать на возмущения, чем хорошо настроенная ПИД-система.
Мертвая зона
Многие контуры ПИД управляют механическим устройством (например, клапаном). Механическое обслуживание может быть основной статьей расходов, а износ приводит к ухудшению управления в виде заедания или люфта в механическом ответе на входной сигнал. Скорость механического износа в основном зависит от того, как часто устройство активируется для внесения изменений. Если износ является существенной проблемой, контур ПИД может иметь мертвую зону выхода , чтобы уменьшить частоту активации выхода (клапана). Это достигается путем модификации контроллера для поддержания его выхода стабильным, если изменение будет небольшим (в пределах определенного диапазона мертвой зоны). Расчетный выход должен покинуть мертвую зону, прежде чем фактический выход изменится.
Шаг изменения заданного значения
Пропорциональные и производные члены могут вызывать чрезмерное движение на выходе, когда система подвергается мгновенному ступенчатому увеличению ошибки, например, большому изменению уставки. В случае производного члена это происходит из-за взятия производной ошибки, которая очень велика в случае мгновенного ступенчатого изменения. В результате некоторые алгоритмы ПИД включают некоторые из следующих модификаций:
- Изменение заданного значения
- В этой модификации заданное значение постепенно перемещается от своего старого значения к новому указанному значению с использованием линейной или дифференциальной функции первого порядка. Это позволяет избежать разрыва, присутствующего в простом ступенчатом изменении.
- Производная переменной процесса
- В этом случае ПИД-регулятор измеряет производную измеренной PV, а не производную ошибки. Эта величина всегда непрерывна (т.е. никогда не имеет ступенчатого изменения в результате изменения уставки). Эта модификация является простым случаем взвешивания уставки.
- Взвешивание заданного значения
- Взвешивание заданного значения добавляет регулируемые факторы (обычно от 0 до 1) к заданному значению в ошибке в пропорциональном и производном элементе контроллера. Ошибка в интегральном члене должна быть истинной ошибкой управления, чтобы избежать ошибок управления в установившемся режиме. Эти два дополнительных параметра не влияют на реакцию на возмущения нагрузки и шум измерения и могут быть настроены для улучшения реакции заданного значения контроллера.
Прямая связь
Производительность системы управления можно улучшить, объединив управление обратной связью (или замкнутым контуром) ПИД-регулятора с управлением прямой связью (или разомкнутым контуром). Знания о системе (например, желаемое ускорение и инерция) можно передать вперед и объединить с выходом ПИД для улучшения общей производительности системы. Значение прямой связи само по себе часто может обеспечить большую часть выходного сигнала контроллера. ПИД-регулятор в первую очередь должен компенсировать любую разницу или ошибку, оставшуюся между заданным значением (SP) и реакцией системы на управление разомкнутым контуром. Поскольку выход прямой связи не зависит от обратной связи процесса, он никогда не может вызвать колебания системы управления, тем самым улучшая реакцию системы, не влияя на устойчивость. Прямая связь может быть основана на заданном значении и на дополнительных измеренных возмущениях. Взвешивание заданного значения является простой формой прямой связи.
Например, в большинстве систем управления движением для ускорения контролируемой механической нагрузки требуется больше силы от привода. Если ПИД-регулятор контура скорости используется для управления скоростью нагрузки и управления силой, прилагаемой приводом, то полезно взять желаемое мгновенное ускорение, соответствующим образом масштабировать это значение и добавить его к выходу ПИД-регулятора контура скорости. Это означает, что всякий раз, когда нагрузка ускоряется или замедляется, пропорциональное количество силы задается приводом независимо от значения обратной связи. ПИД-контур в этой ситуации использует информацию обратной связи для изменения объединенного выхода с целью уменьшения оставшейся разницы между заданным значением процесса и значением обратной связи. Работая вместе, объединенный контроллер прямой связи с открытым контуром и ПИД-регулятор с закрытым контуром могут обеспечить более отзывчивую систему управления.
Безударная операция
ПИД-регуляторы часто реализуются с функцией инициализации «без ударов», которая пересчитывает интегральный член аккумулятора для поддержания согласованного выходного сигнала процесса при изменении параметров. [33] Частичная реализация заключается в сохранении интегрального коэффициента усиления, умноженного на ошибку, вместо сохранения ошибки и последующего умножения на интегральный коэффициент усиления, что предотвращает прерывистый выходной сигнал при изменении коэффициента усиления I, но не коэффициентов усиления P или D.
Другие улучшения
В дополнение к прямой связи, ПИД-регуляторы часто улучшаются с помощью таких методов, как планирование усиления ПИД (изменение параметров в различных рабочих условиях), нечеткая логика или логика вычислительных глаголов. [34] [35] Дополнительные практические проблемы применения могут возникнуть из-за приборов, подключенных к контроллеру. Для достижения адекватной производительности управления требуются достаточно высокая частота дискретизации, точность измерения и точность измерения. Еще один новый метод улучшения ПИД-регулятора заключается в увеличении степени свободы с помощью дробного порядка . Порядок интегратора и дифференциатора добавляет повышенную гибкость контроллеру. [36]
Каскадное управление
Одним из отличительных преимуществ ПИД-регуляторов является то, что два ПИД-регулятора могут использоваться вместе для получения лучших динамических характеристик. Это называется каскадным ПИД-регулированием. Два контроллера находятся в каскаде, когда они расположены таким образом, что один регулирует заданное значение другого. ПИД-регулятор действует как внешний контроллер контура, который управляет основным физическим параметром, таким как уровень или скорость жидкости. Другой контроллер действует как внутренний контроллер контура, который считывает выходной сигнал внешнего контроллера контура как заданное значение, обычно управляя более быстро изменяющимся параметром, расходом или ускорением. Можно математически доказать [ требуется цитата ] , что рабочая частота контроллера увеличивается, а постоянная времени объекта уменьшается при использовании каскадных ПИД-регуляторов. [ неопределенно ] .
Например, циркуляционная ванна с регулируемой температурой имеет два ПИД-регулятора в каскаде, каждый со своим собственным датчиком температуры термопары . Внешний контроллер регулирует температуру воды с помощью термопары, расположенной далеко от нагревателя, где он точно считывает температуру основной массы воды. Погрешность этого ПИД-регулятора представляет собой разницу между желаемой температурой ванны и измеренной температурой. Вместо того чтобы управлять нагревателем напрямую, внешний ПИД-регулятор устанавливает целевую температуру нагревателя для внутреннего ПИД-регулятора. Внутренний ПИД-регулятор регулирует температуру нагревателя с помощью термопары, прикрепленной к нагревателю. Погрешность внутреннего контроллера представляет собой разницу между заданным значением температуры нагревателя и измеренной температурой нагревателя. Его выход управляет фактическим нагревателем, чтобы он оставался вблизи этого заданного значения.
Пропорциональные, интегральные и дифференциальные члены двух контроллеров будут сильно отличаться. Внешний ПИД-контроллер имеет большую постоянную времени — вся вода в баке должна нагреться или остыть. Внутренний контур реагирует гораздо быстрее. Каждый контроллер можно настроить так, чтобы он соответствовал физике системы, которую он контролирует — теплопередача и тепловая масса всего бака или только нагревателя — что даст лучший общий отклик. [37] [38]
Альтернативная номенклатура и формы
Стандартная и параллельная (идеальная) форма
Форма ПИД-регулятора, наиболее часто встречающаяся в промышленности и наиболее соответствующая алгоритмам настройки, — это стандартная форма . В этой форме коэффициент усиления применяется к , и членам, что дает:
где
- это интегральное время
- производное время
В этой стандартной форме параметры имеют ясный физический смысл. В частности, внутреннее суммирование создает новое значение одиночной ошибки, которое компенсируется будущими и прошлыми ошибками. Пропорциональный член ошибки — это текущая ошибка. Член производных компонентов пытается предсказать значение ошибки в секундах (или выборках) в будущем, предполагая, что управление контуром остается неизменным. Интегральный компонент корректирует значение ошибки, чтобы компенсировать сумму всех прошлых ошибок, с намерением полностью устранить их за секунды (или выборки). Полученное компенсированное значение одиночной ошибки затем масштабируется с помощью одиночного усиления для вычисления управляющей переменной.
В параллельной форме, показанной в разделе теории контроллера
параметры усиления связаны с параметрами стандартной формы через и . Эта параллельная форма, где параметры рассматриваются как простые усиления, является наиболее общей и гибкой формой. Однако это также форма, где параметры имеют самую слабую связь с физическим поведением и, как правило, зарезервирована для теоретического рассмотрения ПИД-регулятора. Стандартная форма, несмотря на то, что она немного сложнее математически, более распространена в промышленности.
Взаимное усиление, также известное как пропорциональный диапазон
Во многих случаях управляемая переменная выходного сигнала ПИД-регулятора представляет собой безразмерную дробь между 0 и 100% некоторого максимально возможного значения, а перевод в реальные единицы (такие как скорость накачки или ватты мощности нагревателя) находится за пределами ПИД-регулятора. Однако переменная процесса находится в размерных единицах, таких как температура. В этом случае обычно выражают усиление не как «выход на градус», а скорее в обратной форме пропорционального диапазона , который является «градусами на полный выход»: диапазон, в котором выход изменяется от 0 до 1 (от 0% до 100%). За пределами этого диапазона выходной сигнал насыщен, полностью выключен или полностью включен. Чем уже этот диапазон, тем выше пропорциональное усиление.
Основание производного иска на PV
В большинстве коммерческих систем управления производное действие основано на переменной процесса, а не на ошибке. То есть изменение заданного значения не влияет на производное действие. Это происходит потому, что оцифрованная версия алгоритма создает большой нежелательный всплеск при изменении заданного значения. Если заданное значение постоянно, то изменения в PV будут такими же, как изменения в ошибке. Следовательно, эта модификация не влияет на то, как контроллер реагирует на нарушения процесса.
Основание пропорционального действия на PV
Большинство коммерческих систем управления предлагают возможность также основывать пропорциональное действие исключительно на переменной процесса. Это означает, что только интегральное действие реагирует на изменения уставки. Изменение алгоритма не влияет на то, как контроллер реагирует на нарушения процесса. Основание пропорционального действия на PV устраняет мгновенное и, возможно, очень большое изменение выходного сигнала, вызванное внезапным изменением уставки. В зависимости от процесса и настройки это может быть полезным для реакции на шаг уставки.
Кинг [39] описывает эффективный метод, основанный на диаграммах.
форма Лапласа
Иногда бывает полезно записать ПИД-регулятор в форме преобразования Лапласа :
Наличие ПИД-регулятора, записанного в форме Лапласа, и передаточной функции регулируемой системы позволяет легко определить передаточную функцию замкнутого контура системы.
Серия/взаимодействующая форма
Другим представлением ПИД-регулятора является ряд, или взаимодействующая форма.
где параметры связаны с параметрами стандартной формы через
- , , и
с
- .
Эта форма по сути состоит из последовательно соединенных PD и PI контроллера. Поскольку интеграл требуется для расчета смещения контроллера, эта форма обеспечивает возможность отслеживания внешнего значения смещения, которое требуется для использования для правильной реализации расширенных схем управления с несколькими контроллерами.
Дискретная реализация
Анализ для проектирования цифровой реализации ПИД-регулятора в микроконтроллере (MCU) или устройстве FPGA требует дискретизации стандартной формы ПИД-регулятора . [40] Аппроксимации для производных первого порядка производятся с помощью обратных конечных разностей и дискретизируются с периодом выборки , k — индекс выборки.
Дифференцируя обе части уравнения ПИД с использованием обозначений Ньютона , получаем:
Производные члены аппроксимируются как,
Так,
Применяя обратную разницу снова, получаем:
Упрощая и перегруппируя члены приведенного выше уравнения, в конечном итоге получаем алгоритм реализации дискретизированного ПИД-регулятора в микроконтроллере:
или:
ул
Примечание: Этот метод фактически решает, где — константа, не зависящая от t. Эта константа полезна, когда вы хотите иметь управление запуском и остановкой в контуре регулирования. Например, установка Kp,Ki и Kd в 0 сохранит u(t) постоянным. Аналогично, когда вы хотите запустить регулирование в системе, где ошибка уже близка к 0 с u(t) не равным нулю, это предотвращает отправку выхода в 0.
Псевдокод
Вот очень простая и понятная группа псевдокода, которую легко поймет неспециалист: [ необходима ссылка ]
- Кр - пропорциональный коэффициент усиления
- Ki - интегральный коэффициент усиления
- Kd - производный прирост
- dt - интервал времени цикла (предполагается разумный масштаб) [b]
предыдущая_ошибка := 0интеграл := 0петля: ошибка := заданное значение − измеренное_значение пропорциональный := ошибка; интеграл := интеграл + ошибка × dt производная := (ошибка - предыдущая_ошибка) / dt выход := Kp × пропорциональный + Ki × интегральный + Kd × производный предыдущая_ошибка := ошибка ждать(дт) перейти к циклу
Ниже приведен псевдокод, иллюстрирующий реализацию ПИД-регулятора, рассматривающего ПИД-регулятор как БИХ- фильтр:
Z -преобразование ПИД можно записать как ( — время выборки):
и выражается в форме БИХ (в соответствии с дискретной реализацией, показанной выше):
Затем мы можем вывести рекурсивную итерацию, часто встречающуюся в реализации ПЛИС [41]
A0 := Kp + Ki*dt + Kd/dtA1 := -Kp - 2*Kd/dtA2 := Кд/дтошибка[2] := 0 // е(t-2)ошибка[1] := 0 // е(t-1)ошибка[0] := 0 // е(т)output := u0 // Обычно текущее значение приводапетля: ошибка[2] := ошибка[1] ошибка[1] := ошибка[0] ошибка[0] := заданное значение − измеренное_значение вывод := вывод + A0 * ошибка[0] + A1 * ошибка[1] + A2 * ошибка[2] ждать(дт) перейти к циклу
Здесь Kp — безразмерное число, Ki выражается в , а Kd выражается в с. При выполнении регулирования, когда привод и измеряемое значение не находятся в одной и той же единице (например, регулирование температуры с использованием двигателя, управляющего клапаном), Kp, Ki и Kd могут быть скорректированы с помощью коэффициента преобразования единиц. Также может быть интересно использовать Ki в его обратной форме (время интегрирования). Вышеуказанная реализация позволяет реализовать контроллер только I, что может быть полезно в некоторых случаях.
В реальном мире это преобразование D-to-A и передача в контролируемый процесс в качестве управляемой переменной (MV). Текущая ошибка сохраняется в другом месте для повторного использования в следующей дифференциации, затем программа ждет, пока не пройдет dt секунд с момента запуска, и цикл начинается снова, считывая новые значения для PV и уставки и вычисляя новое значение для ошибки. [42]
Обратите внимание, что для реального кода использование «wait(dt)» может быть неуместным, поскольку оно не учитывает время, затрачиваемое самим алгоритмом во время цикла, или, что более важно, любые упреждения, задерживающие алгоритм.
Распространенной проблемой при использовании является реакция на производную нарастающего или падающего фронта уставки, как показано ниже:
Типичным решением является фильтрация производного действия с использованием фильтра нижних частот с постоянной времени, где :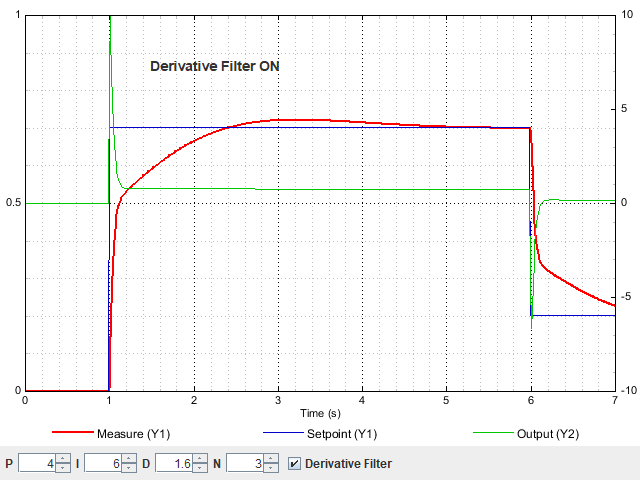
Вариант вышеприведенного алгоритма, использующий фильтр с бесконечной импульсной характеристикой (БИХ) для производной:
A0 := Kp + Ki*dtА1 := -Крошибка[2] := 0 // е(t-2)ошибка[1] := 0 // е(t-1)ошибка[0] := 0 // е(т)output := u0 // Обычно текущее значение приводаA0d := Kd/dtA1d := - 2.0*Kd/dtA2d := Kd/dtН := 5tau := Kd / (Kp*N) // постоянная времени БИХ-фильтраальфа := dt / (2*тау)д0 := 0д1 := 0фд0 := 0фд1 := 0петля: ошибка[2] := ошибка[1] ошибка[1] := ошибка[0] ошибка[0] := заданное значение − измеренное_значение // ПИ вывод := вывод + A0 * ошибка[0] + A1 * ошибка[1] // Фильтрованный D д1 := д0 d0 := A0d * ошибка[0] + A1d * ошибка[1] + A2d * ошибка[2] фд1 := фд0 fd0 := ((альфа) / (альфа + 1)) * (d0 + d1) - ((альфа - 1) / (альфа + 1)) * fd1 выход := выход + fd0 ждать(дт) перейти к циклу
Смотрите также
Примечания
- ^ Единственным исключением является случай, когда целевое значение совпадает со значением, полученным при нулевом выходе контроллера.
- ^ Обратите внимание, что для очень малых интервалов (например, 60 Гц/ сек) результирующее значение производной будет чрезвычайно большим и на порядки больше, чем пропорциональные или интегральные компоненты. Корректировка этого значения для производной (например, умножение на 1000) или изменение деления на умножение, скорее всего, даст желаемые результаты. Это справедливо для всего представленного здесь псевдокода.
Ссылки
- ^ Араки, М. (2009). «Системы управления, робототехника и автоматизация – Том VII - ПИД-регулирование» (PDF) . Япония: Киотский университет.
- ^ "9.3: Настройка ПИД с помощью классических методов". Engineering LibreTexts . 2020-05-19 . Получено 2024-05-31 .
- ^ Хиллс, Ричард Л. (1996), Энергия ветра , Cambridge University Press
- ^ Ричард Э. Беллман (8 декабря 2015 г.). Адаптивные процессы управления: путеводитель. Princeton University Press. ISBN 9781400874668.
- ^ abcdef Беннетт, Стюарт (1996). "Краткая история автоматического управления" (PDF) . Журнал IEEE Control Systems Magazine . 16 (3): 17–25. doi :10.1109/37.506394. Архивировано из оригинала (PDF) 2016-08-09 . Получено 2014-08-21 .
- ^ Максвелл, Дж. К. (1868). «О губернаторах» (PDF) . Труды Королевского общества . 100 .
- ^ Newpower, Anthony (2006). Iron Men and Tin Fish: Гонка за создание лучшей торпеды во время Второй мировой войны . Praeger Security International. ISBN 978-0-275-99032-9.стр. цитируя Грея, Эдвина (1991), «Дьявольское устройство: Роберт Уайтхед и история торпеды» , Аннаполис, Мэриленд: Военно-морской институт США, стр. 33.
- ↑ Sleeman, CW (1880), Torpedoes and Torpedo Warfare, Portsmouth: Griffin & Co., стр. 137–138,
что составляет то, что называется секретом рыбьей торпеды.
- ^ "Краткая история автоматизации зданий". Архивировано из оригинала 2011-07-08 . Получено 2011-04-04 .
- ^ Минорский, Николас (1922). «Курсовая устойчивость автоматически управляемых тел». Журнал Американского общества военно-морских инженеров . 34 (2): 280–309. doi :10.1111/j.1559-3584.1922.tb04958.x.
- ^ Беннетт 1993, стр. 67 harvnb error: no target: CITEREFBennett1993 (help)
- ^ Беннетт, Стюарт (июнь 1986 г.). История техники управления, 1800-1930 гг . IET. стр. 142–148. ISBN 978-0-86341-047-5.
- ^ Шински, Ф. Грег (2004), Сила обратной связи с внешним сбросом (PDF) , Control Global
- ^ Нойхаус, Рудольф. "Diode Laser Locking and Linewidth Narrowing" (PDF) . Получено 8 июня 2015 г.
- ^ "Система управления положением" (PDF) . Кафедра электротехники и электроники Университета Хаджеттепе. Архивировано из оригинала (PDF) 2014-05-13.
- ^ Kebriaei, Reza; Frischkorn, Jan; Reese, Stefanie; Husmann, Tobias; Meier, Horst; Moll, Heiko; Theisen, Werner (2013). «Численное моделирование порошковых металлургических покрытий на кольцевых деталях, интегрированных с прокаткой колец». Material Processing Technology . 213 (1): 2015–2032. doi :10.1016/j.jmatprotec.2013.05.023.
- ^ Липтак, Бела Г. (2003). Справочник инженера-изготовителя приборов: Управление процессами и оптимизация (4-е изд.). CRC Press. стр. 108. ISBN 0-8493-1081-4.
- ^ «Введение: проектирование ПИД-регулятора». Мичиганский университет.
- ^ Тим Уэскотт (октябрь 2000 г.). «ПИД без докторской степени» (PDF) . EE Times-Индия.
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) - ^ ab Bechhoefer, John (2005). «Обратная связь для физиков: учебное эссе по управлению». Reviews of Modern Physics . 77 (3): 783–835. Bibcode : 2005RvMP...77..783B. CiteSeerX 10.1.1.124.7043 . doi : 10.1103/revmodphys.77.783.
- ^ abc Skogestad, Sigurd (2003). "Простые аналитические правила для редукции модели и настройки ПИД-регулятора" (PDF) .
- ^ ab «Обзор методов автонастройки реле для настройки ПИД-регуляторов».
- ^ Киам Хеонг Анг; Чонг, Г.; Юн Ли (2005). «Анализ, проектирование и технология систем ПИД-регулирования» (PDF) . IEEE Transactions on Control Systems Technology . 13 (4): 559–576. doi :10.1109/TCST.2005.847331. S2CID 921620.
- ^ Jinghua Zhong (весна 2006 г.). "PID Controller Tuning: A Short Tutorial" (PDF) . Архивировано из оригинала (PDF) 2015-04-21 . Получено 2011-04-04 .
{{cite journal}}: Цитировать журнал требует|journal=( помощь ) - ^ Острем, К.Дж.; Хэгглунд, Т. (июль 1984 г.). «Автоматическая настройка простых регуляторов». Тома трудов МФБ . 17 (2): 1867–1872. дои : 10.1016/S1474-6670(17)61248-5 .
- ^ Хорнси, Стивен (29 октября 2012 г.). «Обзор методов автонастройки реле для настройки ПИД-регуляторов». Переосмысление . 5 (2).
- ^ Bequette, B. Wayne (2003). Process Control: Modeling, Design, and Simulation . Upper Saddle River, New Jersey: Prentice Hall. стр. 129. ISBN 978-0-13-353640-9.
- ^ Хейнянен, Ээро (октябрь 2018 г.). Метод автоматической настройки ПИД-регулятора с учетом оптимизации Лууса-Яаколы (PDF) (ред. магистерской диссертации). Тампере, Финляндия: Технологический университет Тампере . Получено 1 февраля 2019 г.
- ^ Ли, Юн; Анг, Киам Хеонг; Чонг, Грегори CY (февраль 2006 г.). «Патенты, программное обеспечение и оборудование для ПИД-регулирования: обзор и анализ современного искусства» (PDF) . Журнал IEEE Control Systems . 26 (1): 42–54. doi :10.1109/MCS.2006.1580153. S2CID 18461921.
- ^ Солтес, Кристиан (январь 2012 г.). Об автоматизации процедуры настройки ПИД ( лицензиат theis). Лундский университет . 847ca38e-93e8-4188-b3d5-8ec6c23f2132.
- ^ Li, Y. и Ang, KH и Chong, GCY (2006) Анализ и проектирование систем ПИД-регулирования — проблемы, средства устранения и будущие направления. Журнал IEEE Control Systems, 26 (1). стр. 32-41. ISSN 0272-1708
- ^ Купер, Дуглас. "Интегральное (сброс) намотка, логика оболочки и форма скорости PI" . Получено 18.02.2014 .
- ^ Купер, Дуглас. "ПИ-управление теплообменником". Практическое управление процессами от Control Guru . Получено 27.02.2014 .
- ^ Янг, Т. (июнь 2005 г.). «Архитектуры контроллеров вычислительных глаголов: на пути к новой парадигме интеллектуального управления». Международный журнал вычислительного познания . 3 (2): 74–101. CiteSeerX 10.1.1.152.9564 .
- ^ Лян, Илун; Ян, Тао (2009). «Управление топливным отжигом с использованием вычислительных ПИД-регуляторов глаголов». Труды 3-й Международной конференции по борьбе с подделками, безопасности и идентификации в коммуникациях . Asid'09: 417–420. ISBN 9781424438839.
- ^ Tenreiro Machado JA, et al. (2009). «Некоторые применения дробного исчисления в инженерии». Математические проблемы в инженерии . 2010 : 1–34. doi : 10.1155/2010/639801 . hdl : 10400.22/4306 .
- ^ [1] Основы каскадного управления | Иногда два контроллера могут лучше справляться с поддержанием одной переменной процесса там, где вам нужно. | Вэнс Ван Дорен, доктор наук, инженер-электрик | 17 АВГУСТА 2014 Г.
- ^ [2] | Преимущества каскадного управления | 22 сентября 2020 г. | Уотлоу
- ^ Кинг, Майк (2011). Управление процессами: практический подход . Wiley. стр. 52–78. ISBN 978-0-470-97587-9.
- ^ "Проектирование и анализ дискретных ПИ- и ПИД-регуляторов для цифровой реализации" . Scribd.com . Получено 2011-04-04 .
- ^ Такур, Бхушана. Аппаратная реализация [sic] ПИД-регулятора на базе ПЛИС (PDF) .
- ^ "PID-управление процессом, пример "Круиз-контроля"". CodeProject. 2009 . Получено 4 ноября 2012 .
- Бекетт, Б. Уэйн (2006). Управление процессами: моделирование, проектирование и имитация . Prentice Hall PTR. ISBN 9789861544779.
Дальнейшее чтение
- Липтак, Бела (1995). Справочник инженера-изготовителя приборов: Управление процессами . Раднор, Пенсильвания: Chilton Book Company. стр. 20–29. ISBN 978-0-8019-8242-2.
- Тан, Кок Кионг; Ван Цин-Го; Ханг Чан Чи (1999). Достижения в области ПИД-регулирования . Лондон, Великобритания: Springer-Verlag. ISBN 978-1-85233-138-2.
- King, Myke (2010). Process Control: A Practical Approach. Чичестер, Великобритания: John Wiley & Sons Ltd. ISBN 978-0-470-97587-9.
- Ван Дорен, Вэнс Дж. (1 июля 2003 г.). «Основы настройки контуров». Control Engineering .
- Селлерс, Дэвид. "Обзор пропорционального, интегрального и производного управления и предложения по его успешному применению и внедрению" (PDF) . Архивировано из оригинала (PDF) 7 марта 2007 г. . Получено 2007-05-05 .
- Грэм, Рон; Майк Макхью (2005-10-03). "FAQ по настройке ПИД-регулятора". Майк Макхью. Архивировано из оригинала 6 февраля 2005 г. Получено 2009-01-05 .
- Эйдан О'Двайер (2009). Справочник правил настройки ПИ- и ПИД-регуляторов (PDF) (3-е изд.). Imperial College Press. ISBN 978-1-84816-242-6.
Внешние ссылки
- Настройка ПИД с помощью Mathematica
- Настройка ПИД с использованием Python
- Принципы ПИД-регулирования и настройки
- Введение в ключевые термины, связанные с ПИД-регулированием температуры
Учебники PID
- ПИД-регулирование в MATLAB/Simulink и Python с TCLab
- Что вообще такое этот ПИД-регулятор? Статья в разделе «Электронный дизайн»
- Показывает, как построить ПИД-регулятор с помощью базовых электронных компонентов (стр. 22)
- PID без степени доктора наук
- ПИД-регулирование с помощью MATLAB и Simulink
- ПИД с одним операционным усилителем
- Проверенные методы и передовой опыт ПИД-регулирования
- Принципы ПИД-регулирования и настройки
- Руководство по настройке ПИД-регулятора: передовой подход к пониманию и настройке ПИД-регуляторов
- Майкл Барр (2002-07-30), Введение в замкнутый контур управления, программирование встраиваемых систем, архивировано из оригинала 2010-02-09
- Jinghua Zhong, Машиностроение, Университет Пердью (весна 2006 г.). "Настройка ПИД-регулятора: краткое руководство" (PDF) . Архивировано из оригинала (PDF) 2015-04-21 . Получено 2013-12-04 .
{{cite web}}: CS1 maint: multiple names: authors list (link) - Введение в P,PI,PD и PID-регуляторы с MATLAB










































































![{\displaystyle u(t_{k})=u(t_{k-1})+K_{p}\left[\left(1+{\dfrac {\Delta t}{T_{i}}}+{\dfrac {T_{d}}{\Delta t}}\right)e(t_{k})+\left(-1-{\dfrac {2T_{d}}{\Delta t}}\right)e(t_{k-1})+{\dfrac {T_{d}}{\Delta t}}e(t_{k-2})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)






![{\displaystyle u[n]=u[n-1]+\left(K_{p}+K_{i}\Delta _{t}+{\dfrac {K_{d}}{\Delta _{t}}}\right)\epsilon [n]+\left(-K_{p}-{\dfrac {2K_{d}}{\Delta _{t}}}\right)\epsilon [n-1]+{\dfrac {K_{d}}{\Delta _{t}}}\epsilon [n-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a1135841f70c0c0173ec9271971f6bea3c20830)




