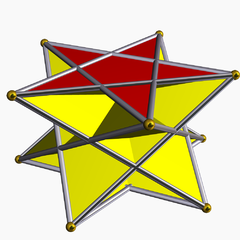
Пентаграмма скрещенная антипризма
| Равномерная пентаграмма скрещенная антипризма | |
|---|---|
 | |
| Тип | Призматический однородный многогранник |
| Элементы | F = 12, E = 20 В = 10 (χ = 2) |
| Лица по сторонам | 10{3}+2{ 5 / 2 } |
| Символ Шлефли | с{2, 10 / 3 } ср{2, 5 / 3 } |
| Символ Витхоффа | | 2 2 5 / 3 |
| Диаграмма Коксетера |       =  |
| Симметрия | D 5h , [5,2], (*522), порядок 20 |
| Группа вращения | D 5 , [5,2] + , (552), порядок 10 D 5d |
| Индекс ссылок | У 80(а) |
| Двойной | Пентаграммный вогнутый трапецоэдр |
| Характеристики | невыпуклый |
 Вершинная фигура 3.3.3.5 / 3 или 3.3.3.- 5 / 2 | |
В геометрии пентаграммная скрещенная антипризма является одной из бесконечного множества невыпуклых антипризм, образованных сторонами треугольников и двумя правильными звездчатыми многоугольниками , в данном случае двумя пентаграммами .
Она отличается от пентаграммной антипризмы тем, что имеет противоположную ориентацию двух пентаграмм.
Этот многогранник идентифицируется индексированным именем U 80 как однородный многогранник .
 Альтернативное изображение с полыми пентаграммами. |
Пентаграммная скрещенная антипризма может быть вписана в икосаэдр и имеет десять треугольных граней, общих с большим икосаэдром . Она имеет то же расположение вершин , что и пентагональная антипризма . Фактически, ее можно рассматривать как парабидоуменьшенный большой икосаэдр .
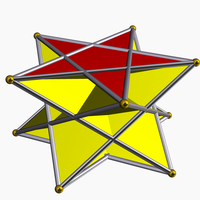Пентаграмма скрещенная антипризма |  Большой икосаэдр , раскрашенный с симметрией D 5d |
Смотрите также
Внешние ссылки
- Вайсштейн, Эрик В. "Пентаграмматическая скрещенная антипризма". MathWorld .
- http://www.mathconsult.ch/showroom/unipoly/80.html
- http://bulatov.org/polyhedra/uniform/u05.html
- https://web.archive.org/web/20050313234519/http://www.math.technion.ac.il/~rl/kaleido/data/05.html
 | Эта статья о многогранниках — заглушка . Вы можете помочь Википедии, расширив ее. |
