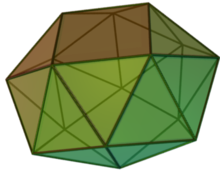
Плосконосая квадратная антипризма
85-й Джонсон солидный (26 граней)
Плосконосая квадратная антипризма
ТипДжонсон
Дж 84 – Дж 85 – Дж 86
Лица24 треугольника
2 квадрата
Края40
Вершины16
Конфигурация вершины 8 × 3 5 + 8 × 3 4 × 4 {\displaystyle 8\times 3^{5}+8\times 3^{4}\times 4}
Группа симметрии Д 4 г {\displaystyle D_{4d}}
Характеристикивыпуклый
Сеть
3D модель плосконосой квадратной антипризмы

В геометрии плосконосая квадратная антипризма — это тело Джонсона , которое может быть построено путем плосконосой квадратной антипризмы . Это одно из элементарных тел Джонсона, которые не возникают из манипуляций «вырезать и вставить» Платоновых и Архимедовых тел , хотя оно является родственником икосаэдра , который имеет четырехкратную симметрию вместо трехкратной.

Строительство и недвижимость

Плосконосый — это процесс построения многогранников путем отрезания граней ребер, их скручивания, а затем присоединения равносторонних треугольников к их ребрам. [1] Как следует из названия, плосконосая квадратная антипризма строится путем придавливания квадратной антипризмы , [2] и это построение приводит к 24 равносторонним треугольникам и 2 квадратам в качестве ее граней. [3] Тела Джонсона — это выпуклые многогранники, грани которых являются правильными, и плосконосая квадратная антипризма является одним из них, обозначенным как , 85-е тело Джонсона. [4] Дж. 85 {\displaystyle J_{85}}

Пусть будет положительным корнем кубического многочлена Кроме того, пусть определяется как Тогда декартовы координаты плосконосой квадратной антипризмы с длиной ребра 2 задаются объединением орбит точек под действием группы, порожденной поворотом вокруг оси - на 90° и поворотом на 180° вокруг прямой, перпендикулярной оси - и составляющей угол 22,5° с осью - . [5] Она имеет трехмерную симметрию диэдральной группы порядка 16. [2] к ≈ 0,82354 {\displaystyle k\приблизительно 0,82354} 9 х 3 + 3 3 ( 5 − 2 ) х 2 − 3 ( 5 − 2 2 ) х − 17 3 + 7 6 . {\displaystyle 9x^{3}+3{\sqrt {3}}\left(5-{\sqrt {2}}\right)x^{2}-3\left(5-2{\sqrt {2}}\right)x-17{\sqrt {3}}+7{\sqrt {6}}.} час ≈ 1.35374 {\displaystyle h\приблизительно 1,35374} час = 2 + 8 + 2 3 к − 3 ( 2 + 2 ) к 2 4 3 − 3 к 2 . {\displaystyle h={\frac {{\sqrt {2}}+8+2{\sqrt {3}}k-3\left(2+{\sqrt {2}}\right)k^{2}}{4{\sqrt {3-3k^{2}}}}}.} ( 1 , 1 , час ) , ( 1 + 3 к , 0 , час − 3 − 3 к 2 ) {\displaystyle (1,1,h),\,\left(1+{\sqrt {3}}k,0,h-{\sqrt {3-3k^{2}}}\right)} з {\displaystyle z} з {\displaystyle z} х {\displaystyle x} Д 4 г {\displaystyle D_{4d}}

Площадь поверхности и объем плосконосой квадратной антипризмы с длиной ребра можно рассчитать следующим образом: [3] а {\displaystyle а} А = ( 2 + 6 3 ) а 2 ≈ 12.392 а 2 , В ≈ 3.602 а 3 . {\displaystyle {\begin{aligned}A=\left(2+6{\sqrt {3}}\right)a^{2}&\approx 12.392a^{2},\\V&\approx 3.602a^{3}.\end{aligned}}}

Ссылки

  1. ^ Холм, Одун (2010). Геометрия: наше культурное наследие. Springer. стр. 99. doi :10.1007/978-3-642-14441-7. ISBN 978-3-642-14441-7.
  2. ^ ab Johnson, Norman W. (1966). «Выпуклые многогранники с правильными гранями». Canadian Journal of Mathematics . 18 : 169– 200. doi :10.4153/cjm-1966-021-8. MR  0185507. Zbl  0132.14603.
  3. ^ ab Берман, Мартин (1971). «Выпуклые многогранники с правильными гранями». Журнал Института Франклина . 291 (5): 329– 352. doi :10.1016/0016-0032(71)90071-8. MR  0290245.
  4. ^ Фрэнсис, Даррил (2013). "Твердые тела Джонсона и их аббревиатуры". Word Ways . 46 (3): 177.
  5. ^ Тимофеенко, АВ (2009). "Неплатоновы и неархимедовы несоставные многогранники". Журнал математических наук . 162 (5): 725. doi :10.1007/s10958-009-9655-0. S2CID  120114341.
Retrieved from "https://en.wikipedia.org/w/index.php?title=Snub_square_antiprism&oldid=1234006160"