Runcinated 120-клеточный

Четыре бега
Ортогональные проекции в плоскости Коксетера H ₃
120-ячеечный	Runcinated 120-ячеечный (Расширенный 120-ячеечный)	Runcitucated 120-ячеечный
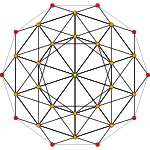600-ячеечный	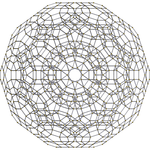Runcitucated 600-ячеечный	Усеченный 120-ячеечный

В четырехмерной геометрии многогранник из 120 ячеек (или многогранник из 600 ячеек ) представляет собой выпуклый однородный 4-мерный многогранник , являющийся многогранником из 120 ячеек (усечением 3-го порядка) .

Существует 4 степени рунцинаций 120-клеточного ряда, включая перестановки, усечения и кантелляции.

Свернутый 120-ячеечный многогранник можно рассматривать как расширение, примененное к обычному 4-ячеистому многограннику, 120-ячеистому или 600-ячеистому.

Runcinated 120-ячеечный

Runcinated 120-ячеечный
Тип	Однородный 4-многогранник
Единый индекс	38
Диаграмма Коксетера
Клетки	2640 всего: 120 5.5.5 720 4.4.5 1200 4.4.3 600 3.3.3
Лица	7440: 2400{3}+3600{4}+ 1440{5}
Края	7200
Вершины	2400
Вершинная фигура	Равносторонний треугольный антиподий
Символ Шлефли	т _0,3 {5,3,3}
Группа симметрии	H ₄ , [3,3,5], порядок 14400
Характеристики	выпуклый

Runcinated 120-ячейковый или малый disprismatohexacosihecatonicosachoron является однородным 4-политопом . Он имеет 2640 ячеек: 120 додекаэдров , 720 пятиугольных призм , 1200 треугольных призм и 600 тетраэдров . Его вершинная фигура — неоднородная треугольная антипризма (равносторонний треугольный антиподий): ее основания представляют собой додекаэдр и тетраэдр, а его боковые стороны — три треугольные призмы и три пятиугольные призмы.

Альтернативные названия

Runcinated 120-cell / Runcinated 600-cell ( Норман В. Джонсон )
- Runcinated hecatonicosachoron / Runcinated dodecacontachoron / Runcinated hexacosichoron / Runcinated polydodecahedron / Runcinated polytetrahedron
Малый диприматогексакосихекатоникосохорон (сокращенно: sidpixhi) (Джордж Ольшевский, Джонатан Бауэрс) ^[1]

Изображения

Диаграмма Шлегеля (показаны только тетраэдрические ячейки)

Многогранные кольца
Клетки на 5-кратной оси	Клетки на 3-й оси	Клетки на 2-й оси

Ортогональные проекции в плоскостях Кокстера
Н3	А2/В3	А3/В2

Runcitucated 120-ячеечный

Runcitucated 120-ячеечный
Тип	Однородный 4-многогранник
Единый индекс	43
Диаграмма Коксетера
Клетки	2640 всего: 120 (3.10.10) 720 (4.4.10) 1200 (3.4.4) 600 (3.4.3.4)
Лица	13440: 4800{3}+7200{4}+ 1440{10}
Края	18000
Вершины	7200
Вершинная фигура	Неправильная прямоугольная пирамида
Символ Шлефли	т _0,1,3 {5,3,3}
Группа симметрии	H ₄ , [3,3,5], порядок 14400
Характеристики	выпуклый

Runciturcated 120-ячейковый или призматоромбатированный гексакосихорон является однородным 4-политопом . Он содержит 2640 ячеек: 120 усеченных додекаэдров , 720 десятиугольных призм , 1200 треугольных призм и 600 кубооктаэдров . Его вершинная фигура — неправильная прямоугольная пирамида с одним усеченным додекаэдром, двумя десятиугольными призмами, одной треугольной призмой и одним кубооктаэдром.

Альтернативные названия

Runcicantellated 600-клеточный ( Норман В. Джонсон )
Призматоромбатированный гексакосихорон (сокращение: prix) (Джордж Ольшевский, Джонатан Бауэрс) ^[2]

Изображения

Диаграмма Шлегеля (показаны только треугольные призмы)

Ортогональные проекции в плоскостях Кокстера
Н3	А2/В3	А3/В2

Runcitucated 600-ячеечный

Runcitucated 600-ячеечный
Тип	Однородный 4-многогранник
Единый индекс	44
Диаграмма Коксетера
Клетки	2640 всего: 120 3.4.5.4 720 4.4.5 1200 4.4.6 600 3.6.6
Лица	13440: 2400{3}+7200{4}+ 1440{5}+2400{6}
Края	18000
Вершины	7200
Вершинная фигура	Трапециевидная пирамида
Символ Шлефли	т _0,1,3 {3,3,5}
Группа симметрии	H ₄ , [3,3,5], порядок 14400
Характеристики	выпуклый

Runciturcated 600-ячеечный или призматоромбатированный гекатонико-сахорон является однородным 4-политопом . Он состоит из 2640 ячеек : 120 ромбоикосододекаэдров , 600 усеченных тетраэдров , 720 пятиугольных призм и 1200 шестиугольных призм . Он имеет 7200 вершин, 18000 ребер и 13440 граней (2400 треугольников, 7200 квадратов и 2400 шестиугольников).

Альтернативные названия

Runcicantellated 120-клеточный ( Норман В. Джонсон )
Призматоромбатный гекатоникосохорон (сокращение: prahi) (Джордж Ольшевский, Джонатан Бауэрс) ^[3]

Изображения

Диаграмма Шлегеля

Ортогональные проекции в плоскостях Кокстера
Н3	А2/В3	А3/В2

Усеченный 120-ячеечный

Усеченный 120-ячеечный
Тип	Однородный 4-многогранник
Единый индекс	46
Диаграмма Коксетера
Клетки	2640 всего: 120 4.6.10 720 4.4.10 1200 4.4.6 600 4.6.6
Лица	17040 всего: 10800 {4} , 4800 {6} 1440 {10}
Края	28800
Вершины	14400
Вершинная фигура	Хиральный разносторонний тетраэдр
Символ Шлефли	т _0,1,2,3 {3,3,5}
Группа симметрии	H ₄ , [3,3,5], порядок 14400
Характеристики	выпуклый

Омнитрусцированный 120-ячейковый или большой диспризматогексакосигектоникосахорон является выпуклым однородным 4-многогранником , состоящим из 2640 ячеек : 120 усеченных икосододекаэдров , 600 усеченных октаэдров , 720 десятиугольных призм и 1200 шестиугольных призм . Он имеет 14400 вершин, 28800 ребер и 17040 граней (10800 квадратов, 4800 шестиугольников и 1440 десятиугольников). Это самый большой непризматический выпуклый однородный 4-многогранник .

Вершины и ребра образуют граф Кэли группы Коксетера H ₄ .

Альтернативные названия

Omnitruncated 120-cell / Omnitruncated 600-cell ( Норман В. Джонсон )
Всеусеченный гекатоникосохорон / Всеусеченный гексакосихорон / Всеусеченный полидодекаэдр / Всеусеченный политетраэдр
Большой диприсматогексакосихекатоникосохорон (сокращение gidpixhi) (Джордж Ольшевский, Джонатан Бауэрс) ^[4]

Изображения

Диаграмма Шлегеля (в центре усеченный икосододекаэдр ) (Ортогональный вид, в центре ячейка десятиугольной призмы .)	Стереографическая проекция (с центром на усеченном икосододекаэдре )

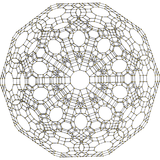Ортогональные проекции в плоскостях Кокстера
Н3	А2/В3	А3/В2

Многогранные кольца
Клетки на 5-кратной оси	Клетки на 3-й оси	Клетки на 2-й оси

Сеть
Усеченный 120-ячеечный	Двойной к усеченному 120-элементному

Модели

Первая полная физическая модель трехмерной проекции усеченной 120-ячеечной системы была создана командой под руководством Дэниела Дадди и Дэвида Рихтера 9 августа 2006 года с использованием системы Zome в Лондонской лаборатории знаний для конференции Bridges Conference 2006 года. ^[5]

Полный курносый 120-элементный

Полный плосконосый 120-клеточный или омнисконосый 120-клеточный , определяемый как чередование омниусеченного 120-клеточного, не может быть сделан однородным, но ему можно придать диаграмму Коксетера, и симметрия [5,3,3] ⁺ , и построенный из 1200 октаэдров , 600 икосаэдров , 720 пятиугольных антипризм , 120 плосконосых додекаэдров , и 7200 тетраэдров , заполняющих пробелы в удаленных вершинах. Он имеет 9840 ячеек, 35040 граней, 32400 ребер и 7200 вершин. ^[6]

Связанные многогранники

Эти многогранники являются частью набора из 15 однородных 4-мерных многогранников с симметрией _H4 :

Многогранники семейства H ₄
120-ячеечный	выпрямленный 120-ячеечный	усеченный 120-ячеечный	кантеллированный 120-ячеечный	120- клеточный	кантит-усеченный 120-ячеечный	runcitucated 120-ячеечный	усеченный 120-ячеечный

{5,3,3}	г{5,3,3}	т{5,3,3}	рр{5,3,3}	т _0,3 {5,3,3}	тр{5,3,3}	т _0,1,3 {5,3,3}	т _0,1,2,3 {5,3,3}


600-ячеечный	выпрямленный 600-элементный	усеченный 600-ячеечный	кантеллированный 600-ячеечный	битусжатый 600-ячеечный	усеченный 600-ячеечный	runcitucated 600-ячейковый	усеченный 600-ячеечный

{3,3,5}	г{3,3,5}	т{3,3,5}	рр{3,3,5}	2т{3,3,5}	тр{3,3,5}	т _0,1,3 {3,3,5}	т _0,1,2,3 {3,3,5}

Примечания

^ Клитизация, (x3o3o5x - sidpixhi)
^ Клитизация, (x3o3x5x - prix)
^ Клитизинг, (x3x3o5x - прахи)
^ Клитизация, (x3x3x5x - gidpixhi)
^ Фотографии модели Zome с усеченной 120/600 ячейкой
^ "S3s3s5s".

Ссылки

Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Документ 22) HSM Coxeter, Правильные и полуправильные многогранники I , [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Документ 23) HSM Coxeter, Правильные и полуправильные многогранники II , [Math. Zeit. 188 (1985) 559-591]
- (Документ 24) HSM Coxeter, Правильные и полуправильные многогранники III , [Math. Zeit. 200 (1988) 3-45]
JH Conway и MJT Guy : Четырехмерные архимедовы многогранники , Труды коллоквиума по выпуклости в Копенгагене, стр. 38 и 39, 1965 г.
NW Johnson : Теория однородных многогранников и сот , докторская диссертация, Университет Торонто, 1966 г.
Четырехмерные архимедовы многогранники (на немецком языке), Марко Мёллер, 2004 г. Кандидатская диссертация [1] m55 m62 m60 m64
Выпуклая однородная полихора на основе гекатоникосахора (120-клеточного) и гексакосихора (600-клеточного) - Модель 38, 44, 47, Георгий Ольшевский.
Клитцинг, Ричард. «Четырехмерные однородные многогранники (полихоры)».x3o3o5x - sidpixhi, x3o3x5x - prix, x3x3o5x - prahi, x3x3x5x - gidpixhi

Внешние ссылки

Однородные многогранники H4 с координатами: t03{5,3,3} t013{3,3,5} t013{5,3,3} t0123{5,3,3}

в т е Фундаментальные выпуклые правильные и однородные многогранники в размерностях 2–10
Семья	А _н	Б _н	Я ₂ (п) / Д _н	Е ₆ / Е ₇ / Е ₈ / Ф ₄ / Соль ₂	Н _н
Правильный многоугольник	Треугольник	Квадрат	п-гон	Шестиугольник	Пентагон
Однородный многогранник	Тетраэдр	Октаэдр • Куб	Демикуб		Додекаэдр • Икосаэдр
Равномерный полихорон	Пентахорон	16-ячеечный • Тессеракт	Демитессеракт	24-ячеечный	120-ячеечный • 600-ячеечный
Однородный 5-многогранник	5-симплекс	5-ортоплекс • 5-куб	5-демикуб
Однородный 6-многогранник	6-симплекс	6-ортоплекс • 6-куб	6-демикуб	1 ₂₂ • 2 ₂₁
Однородный 7-многогранник	7-симплекс	7-ортоплекс • 7-куб	7-демикуб	1 ₃₂ • 2 ₃₁ • 3 ₂₁
Однородный 8-многогранник	8-симплекс	8-ортоплекс • 8-куб	8-демикуб	1 ₄₂ • 2 ₄₁ • 4 ₂₁
Однородный 9-многогранник	9-симплекс	9-ортоплекс • 9-куб	9-демикуб
Однородный 10-многогранник	10-симплекс	10-ортоплекс • 10-куб	10-демикуб
Однородный n - многогранник	н - симплекс	n - ортоплекс • n - куб	н - демикуб	1 _к2 • 2 _к1 • к ₂₁	n - пятиугольный многогранник
Темы: Семейства многогранников • Правильный многогранник • Список правильных многогранников и соединений

[1] Клитизация, (x3o3o5x - sidpixhi)

[2] Клитизация, (x3o3x5x - prix)

[3] Клитизинг, (x3x3o5x - прахи)

[4] Клитизация, (x3x3x5x - gidpixhi)

[5] Фотографии модели Zome с усеченной 120/600 ячейкой

[6] "S3s3s5s".