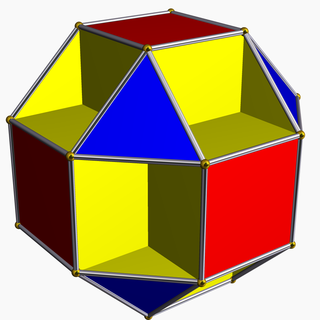
Малый кубокубооктаэдр

Малый кубокубооктаэдр
Тип	Однородный звездчатый многогранник
Элементы	F = 20, E = 48 V = 24 (χ = −4)
Лица по сторонам	8{3}+6{4}+6{8}
Диаграмма Коксетера
Символ Витхоффа	3/2 4 | 4 3 4/3 | 4
Группа симметрии	О , ч , [4,3], *432
Индекс ссылок	У 13 , С 38 , Ж 69
Двойной многогранник	Малый гексахронный икоситетраэдр
Вершинная фигура	4.8.3/2.8
Акроним Bowers	Сокко

В геометрии малый кубокубооктаэдр — это однородный звездчатый многогранник , индексируемый как U ₁₃ . Он имеет 20 граней (8 треугольников , 6 квадратов и 6 восьмиугольников ), 48 ребер и 24 вершины. ^[1] Его вершинная фигура — перекрещенный четырехугольник .

Малый кубокубооктаэдр является огранкой ромбокубооктаэдра . Его квадратные грани и восьмиугольные грани параллельны граням куба , в то время как треугольные грани параллельны граням октаэдра : отсюда и название кубокубооктаэдр . Маленький суффикс служит для того, чтобы отличать его от большого кубокубооктаэдра , который также имеет грани в вышеупомянутых направлениях. ^[2]

Он разделяет расположение вершин со звездчатым усеченным гексаэдром . Кроме того, он разделяет расположение ребер с ромбокубооктаэдром (имеющим общие треугольные грани и 6 квадратных граней) и с малым ромбогексаэдром (имеющим общие восьмиугольные грани).

Ромбокубооктаэдр

Малый кубокубооктаэдр

Малый ромбогексаэдр

Звездчатый усеченный шестигранник

Как предполагает характеристика Эйлера, малый кубикубооктаэдр является тороидальным многогранником рода 3 (топологически это поверхность рода 3), и, таким образом, может быть интерпретирован как (полиэдральное) погружение полиэдральной поверхности рода 3 в дополнение к ее 24 вершинам в 3-пространство. (Окрестность любой вершины топологически является конусом на восьмерке, что не может произойти при погружении. Обратите внимание, что ссылка Рихтера игнорирует этот факт.) Базовый многогранник (игнорируя самопересечения) определяет равномерную мозаику этой поверхности, и поэтому малый кубикубооктаэдр является равномерным многогранником. На языке абстрактных многогранников малый кубикубооктаэдр является точной реализацией этого абстрактного тороидального многогранника, что означает, что он является невырожденным многогранником и что они имеют одну и ту же группу симметрии. Фактически, каждый автоморфизм абстрактной поверхности рода 3 с этой мозаикой реализуется изометрией евклидова пространства.

Поверхности более высокого рода (род 2 или выше) допускают метрику отрицательной постоянной кривизны (по теореме об униформизации ), и универсальное покрытие полученной римановой поверхности является гиперболической плоскостью . Соответствующая мозаика гиперболической плоскости имеет вершинную фигуру 3.8.4.8 (треугольник, восьмиугольник, квадрат, восьмиугольник). Если поверхности задана соответствующая метрика кривизны = −1, покрывающее отображение является локальной изометрией и, таким образом, абстрактная вершинная фигура та же самая. Эта мозаика может быть обозначена символом Витхоффа 3 4 | 4 и изображена справа.

Альтернативно и более тонко, разрезая каждую квадратную грань на 2 треугольника и каждую восьмиугольную грань на 6 треугольников, малый кубикубооктаэдр можно интерпретировать как нерегулярную раскраску комбинаторно регулярной (а не просто равномерной ) мозаики поверхности рода 3 56 равносторонними треугольниками, встречающимися в 24 вершинах, каждая из которых имеет степень 7. ^[3] Эта регулярная мозаика важна, поскольку она является мозаикой квартики Клейна , поверхности рода 3 с наиболее симметричной метрикой (автоморфизмы этой мозаики равны изометриям поверхности), а группа автоморфизмов, сохраняющих ориентацию, этой поверхности изоморфна проективной специальной линейной группе PSL(2,7), что эквивалентно GL(3,2) (группа порядка 168 всех сохраняющих ориентацию изометрий). Обратите внимание, что малый кубокубооктаэдр не является реализацией этого абстрактного многогранника, поскольку он имеет только 24 симметрии, сохраняющие ориентацию (не каждый абстрактный автоморфизм реализуется евклидовой изометрией) – изометрии малого кубокубооктаэдра сохраняют не только треугольную мозаику, но и раскраску, и, следовательно, являются собственной подгруппой полной группы изометрий.

Соответствующая мозаика гиперболической плоскости (универсальное покрытие) — это треугольная мозаика порядка 7. Группа автоморфизмов квартики Клейна может быть расширена (симметрией, которая не реализуется симметрией многогранника, а именно «заменой двух конечных точек ребер, которые делят пополам квадраты и октаэдры»), чтобы получить группу Матье M ₂₄ . ^[4]

• Соединение пяти малых кубокубооктаэдров
• Список однородных многогранников

• Вайсштейн, Эрик В. , «Малый кубикубооктаэдр» («Однородный многогранник») на MathWorld .