Баланс оболочки

Эта статья включает список ссылок , связанных материалов или внешних ссылок , но ее источники остаются неясными, поскольку в ней отсутствуют встроенные цитаты . Пожалуйста, помогите улучшить эту статью, введя более точные цитаты. ( Январь 2020 г. ) ( Узнайте, как и когда удалять это сообщение )

В механике жидкости баланс оболочки может использоваться для определения профиля скорости движущейся жидкости, т. е. того, как скорость жидкости изменяется в зависимости от положения в поперечном сечении потока.

«Оболочка» — это дифференциальный элемент потока. Рассматривая импульс и силы на одной небольшой части, можно интегрировать по потоку, чтобы увидеть более широкую картину потока в целом. Баланс определяет, что входит в оболочку и выходит из нее. Импульс создается внутри оболочки посредством входящей и выходящей из нее жидкости и касательного напряжения . Кроме того, на оболочку действуют давление и гравитационные силы. Из этого можно найти скорость для любой точки поперек потока.

Баланс оболочки может использоваться во многих ситуациях. Например, поток в трубе, поток нескольких жидкостей вокруг друг друга или поток из-за разницы давления. Хотя термины в балансе оболочки и граничных условиях изменятся, базовая настройка и процесс останутся прежними.

Жидкость должна обладать:

• Ламинарный поток
• Никаких изгибов и кривых
• Устойчивое состояние
• Два граничных условия

Граничные условия используются для нахождения констант интегрирования.

• Граница жидкость - твердое тело: Условие прилипания , скорость жидкости у твердого тела равна скорости твердого тела.
• Граница жидкость - газ : напряжение сдвига = 0.
• Граница раздела жидкость-жидкость: одинаковая скорость и касательное напряжение в обеих жидкостях.

Жидкость течет между двумя горизонтальными поверхностями с площадью контакта A и находится с ними в контакте. Используется дифференциальная оболочка высотой Δy (см. схему ниже).

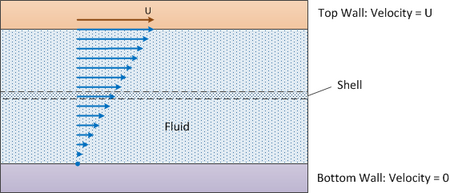
Верхняя поверхность движется со скоростью U, а нижняя поверхность неподвижна.

• Плотность жидкости = ρ
• Вязкость жидкости = μ
• Скорость в направлении x = , показанная диагональной линией выше. Это то, что решает баланс оболочки.${\displaystyle V_{x}}$

• (Скорость импульса на входе) - (скорость импульса на выходе) + (сумма всех сил) = 0

Для выполнения балансировки оболочки выполните следующие основные шаги:

1. Найти импульс от касательного напряжения. (Импульс от касательного напряжения в систему) - (Импульс от касательного напряжения из системы). Импульс от касательного напряжения переходит в оболочку в точке y и покидает систему в точке y  + Δ y . Касательное напряжение = τ _yx , площадь = A , импульс = τ _yx A .
2. Найти импульс из потока. Импульс втекает в систему при x  = 0 и вытекает при x  = L. Поток стационарный. Следовательно, поток импульса при x  = 0 равен моменту потока при x  = L. Следовательно, они сокращаются.
3. Найдите силу тяжести, действующую на оболочку.
4. Найдите силы давления .
5. Подставим в закон сохранения импульса и решим для τ _yx .
6. Применим закон вязкости Ньютона для ньютоновской жидкости τ _yx = - μ ( dV _x / dy ).
7. Интегрируйте, чтобы найти уравнение скорости, и используйте граничные условия, чтобы найти константы интегрирования.

Граница 1: Верхняя поверхность: y = 0 и V _x = U

Граница 2: Нижняя поверхность: y = D и V _x = 0

• "Решения проблем в явлениях переноса: проблемы механики жидкости" . Получено 2007-10-06 .

• Харриотт, Питер; В. МакКейб; Дж. Смит (2004). Операции подразделений химической инженерии: Седьмое издание. McGraw-Hill Professional. С.  68–132 . ISBN 9780072848236.