Уравнение рендеринга

Интегральное уравнение

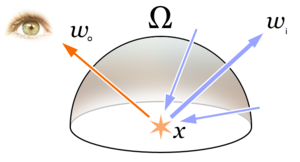
В компьютерной графике уравнение рендеринга представляет собой интегральное уравнение , в котором равновесная яркость , покидающая точку, задается как сумма испускаемой и отраженной яркости в приближении геометрической оптики . Оно было одновременно введено в компьютерную графику Дэвидом Иммелем и др. ^[1] и Джеймсом Каджией ^[2] в 1986 году. Различные реалистичные методы рендеринга в компьютерной графике пытаются решить это уравнение.

Физической основой уравнения рендеринга является закон сохранения энергии . Предполагая, что L обозначает яркость , мы имеем, что в каждом конкретном положении и направлении исходящий свет (L _o ) является суммой испускаемого света (L _e ) и отраженного света (L _r ). Сам отраженный свет является суммой со всех направлений входящего света (L _i ), умноженного на отражение поверхности и косинус угла падения.

Форма уравнения

Уравнение рендеринга можно записать в виде

L_{\text{o}}(\mathbf {x},\omega _{\text{o}},\lambda ,t)=L_{\text{e}}(\mathbf {x},\omega _{\text{o}},\lambda ,t)+L_{\text{r}}(\mathbf {x},\omega _{\text{o}},\lambda ,t)

L_{\text{r}}(\mathbf {x},\omega _{\text{o}},\lambda,t)=\int _{\Omega }f_{\text{r}}(\mathbf {x},\omega _{\text{i}},\omega _{\text{o}},\lambda,t)L_{\text{i}}(\mathbf {x},\omega _{\text{i}},\lambda,t)(\omega _{\text{i}}\cdot \mathbf {n})\operatorname {d} \omega _{\text{i}}

где

$L_{\text{o}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ это полная спектральная яркость длины волны, направленная наружу вдоль направления во времени , из определенного положения $\лямбда$ $\omega _{\text{o}}$ $т$ $\mathbf {x}$
$\mathbf {x}$ это местоположение в пространстве
$\omega _{\text{o}}$ это направление исходящего света
$\лямбда$ это определенная длина волны света
$т$ время
$L_{\text{e}}(\mathbf {x},\omega _{\text{o}},\lambda,t)$ испускается спектральное излучение
$L_{\text{r}}(\mathbf {x} ,\omega _{\text{o}},\lambda ,t)$ это отраженное спектральное излучение
$\int _{\Omega }\dots \operatorname {d} \omega _{\text{i}}$ является интегралом по $\Омега$
$\Омега$ представляет собой единичную полусферу , центрированную вокруг которой , содержащую все возможные значения для где $\mathbf {н}$ $\omega _{\text{i}}$ $\omega _{\text{i}}\cdot \mathbf {n} >0$
$f_{\text{r}}(\mathbf {x} ,\omega _{\text{i}},\omega _{\text{o}},\lambda ,t)$ - это функция распределения двунаправленной отражательной способности , доля света, отраженного от в в определенном положении , времени и на определенной длине волны. $\omega _{\text{i}}$ $\omega _{\text{o}}$ $\mathbf {x}$ $т$ $\лямбда$
$\omega _{\text{i}}$ отрицательное направление входящего света
$L_{\text{i}}(\mathbf {x} ,\omega _{\text{i}},\lambda ,t)$ спектральная яркость длины волны, приходящая внутрь по направлению от направления во времени $\лямбда$ $\mathbf {x}$ $\omega _{\text{i}}$ $т$
$\mathbf {н}$ нормаль к поверхности $\mathbf {x}$
$\omega _{\text{i}}\cdot \mathbf {n}$ - фактор ослабления внешнего излучения из-за угла падения , поскольку световой поток размазывается по поверхности, площадь которой больше площади проекции, перпендикулярной лучу. Это часто записывается как . $\cos \theta _{i}$

Две заслуживающие внимания особенности: его линейность — оно состоит только из умножений и сложений, и его пространственная однородность — оно одинаково во всех положениях и ориентациях. Это означает, что возможен широкий диапазон факторизаций и перестановок уравнения. Это интегральное уравнение Фредгольма второго рода, подобное тем, которые возникают в квантовой теории поля . ^[3]

Обратите внимание на спектральную и временную зависимость этого уравнения — может быть выбрано или интегрировано по разделам видимого спектра для получения, например, трехцветного образца цвета. Значение пикселя для одного кадра в анимации может быть получено путем исправления размытия движения , которое может быть получено путем усреднения по некоторому заданному интервалу времени (путем интегрирования по интервалу времени и деления на длину интервала). ^[4] $L_{\text{o}}$ $т;$ $L_{\text{o}}$

Обратите внимание, что решением уравнения рендеринга является функция . Функция связана с посредством операции трассировки лучей: входящее излучение с некоторого направления в одной точке является исходящим излучением в некоторой другой точке в противоположном направлении. $L_{\text{o}}$ $L_{\text{i}}$ $L_{\text{o}}$

Приложения

Решение уравнения рендеринга для любой заданной сцены является основной проблемой в реалистичном рендеринге . Один из подходов к решению уравнения основан на методах конечных элементов , что приводит к алгоритму излучательности . Другой подход, использующий методы Монте-Карло, привел к появлению множества различных алгоритмов, включая трассировку пути , картографирование фотонов и перенос света Metropolis , среди прочих.

Ограничения

Хотя уравнение является очень общим, оно не охватывает все аспекты отражения света. Некоторые недостающие аспекты включают следующее:

Пропускание , которое происходит, когда свет проходит через поверхность, например, когда он попадает на стеклянный предмет или поверхность воды ,
Рассеивание под поверхностью , где пространственное расположение входящего и исходящего света различно. Поверхности, визуализированные без учета рассеивания под поверхностью, могут выглядеть неестественно непрозрачными — однако, нет необходимости учитывать это, если передача включена в уравнение, поскольку это будет эффективно включать также свет, рассеянный под поверхностью,
Поляризация , при которой различные поляризации света иногда будут иметь разное распределение отражения, например, когда свет отражается от поверхности воды,
Фосфоресценция , которая происходит, когда свет или другое электромагнитное излучение поглощается в один момент и испускается в более поздний момент, обычно с большей длиной волны (если только поглощенное электромагнитное излучение не является очень интенсивным) ,
Интерференция , где проявляются волновые свойства света,
Флуоресценция , где поглощенный и испускаемый свет имеют разные длины волн ,
Нелинейные эффекты, при которых очень интенсивный свет может повысить уровень энергии электрона с большей энергией, чем у одного фотона (это может произойти, если электрон одновременно сталкивается с двумя фотонами), и излучение света с более высокой частотой, чем частота света, который ударяет по поверхности, внезапно становится возможным, и
Эффект Доплера , когда свет, отражающийся от объекта, движущегося с очень высокой скоростью, изменяет свою длину волны: если свет отражается от объекта, движущегося к нему, свет будет смещен в синюю область спектра , а фотоны будут упакованы более плотно, поэтому поток фотонов увеличится; если он отражается от объекта, движущегося от него, он будет смещен в красную область спектра , а поток фотонов уменьшится. Этот эффект становится заметным только на скоростях, сравнимых со скоростью света , что не относится к большинству приложений рендеринга.

Для сцен, которые либо не состоят из простых поверхностей в вакууме, либо для которых время прохождения света является важным фактором, исследователи обобщили уравнение рендеринга, чтобы получить уравнение объемного рендеринга ^[5], подходящее для объемного рендеринга , и уравнение переходного рендеринга ^[6] для использования с данными с камеры времени пролета .

Ссылки

^ Иммел, Дэвид С.; Коэн, Майкл Ф.; Гринберг, Дональд П. (1986). "Метод излучения для недиффузных сред" (PDF) . В Дэвид К. Эванс; Рассел Дж. Атай (ред.). SIGGRAPH '86 . Труды 13-й ежегодной конференции по компьютерной графике и интерактивным технологиям. стр. 133–142. doi :10.1145/15922.15901. ISBN 978-0-89791-196-2. S2CID 7384510.
^ Каджия, Джеймс Т. (1986). "Уравнение рендеринга" (PDF) . В Дэвид К. Эванс; Рассел Дж. Атай (ред.). SIGGRAPH '86 . Труды 13-й ежегодной конференции по компьютерной графике и интерактивным технологиям. стр. 143–150. doi :10.1145/15922.15902. ISBN 978-0-89791-196-2. S2CID 9226468.
^ Уотт, Алан; Уотт, Марк (1992). "12.2.1 Решение трассировки пути для уравнения рендеринга". Advanced Animation and Rendering Techniques: Theory and Practice . Addison-Wesley Professional. стр. 293. ISBN 978-0-201-54412-1.
↑ Оуэн, Скотт (5 сентября 1999 г.). «Отражение: теория и математическая формулировка» . Получено 22 июня 2008 г.
^ Каджия, Джеймс Т.; Фон Герцен, Брайан П. (1984), «Объемные плотности трассировки лучей», ACM SIGGRAPH Computer Graphics , 18 (3): 165–174, CiteSeerX 10.1.1.128.3394 , doi :10.1145/964965.808594
^ Смит, Адам М.; Скорупски, Джеймс; Дэвис, Джеймс (2008). Transient Rendering (PDF) (Технический отчет). Калифорнийский университет в Санта-Крузе. UCSC-SOE-08-26.

Внешние ссылки

Конспект лекций курса Стэнфордского университета CS 348B, Компьютерная графика: Методы синтеза изображений

[1] Иммел, Дэвид С.; Коэн, Майкл Ф.; Гринберг, Дональд П. (1986). "Метод излучения для недиффузных сред" (PDF) . В Дэвид К. Эванс; Рассел Дж. Атай (ред.). SIGGRAPH '86 . Труды 13-й ежегодной конференции по компьютерной графике и интерактивным технологиям. стр. 133–142. doi :10.1145/15922.15901. ISBN 978-0-89791-196-2. S2CID 7384510.

[2] Каджия, Джеймс Т. (1986). "Уравнение рендеринга" (PDF) . В Дэвид К. Эванс; Рассел Дж. Атай (ред.). SIGGRAPH '86 . Труды 13-й ежегодной конференции по компьютерной графике и интерактивным технологиям. стр. 143–150. doi :10.1145/15922.15902. ISBN 978-0-89791-196-2. S2CID 9226468.

[3] Уотт, Алан; Уотт, Марк (1992). "12.2.1 Решение трассировки пути для уравнения рендеринга". Advanced Animation and Rendering Techniques: Theory and Practice . Addison-Wesley Professional. стр. 293. ISBN 978-0-201-54412-1.

[4] Оуэн, Скотт (5 сентября 1999 г.). «Отражение: теория и математическая формулировка» . Получено 22 июня 2008 г.

[5] Каджия, Джеймс Т.; Фон Герцен, Брайан П. (1984), «Объемные плотности трассировки лучей», ACM SIGGRAPH Computer Graphics , 18 (3): 165–174, CiteSeerX 10.1.1.128.3394 , doi :10.1145/964965.808594

[6] Смит, Адам М.; Скорупски, Джеймс; Дэвис, Джеймс (2008). Transient Rendering (PDF) (Технический отчет). Калифорнийский университет в Санта-Крузе. UCSC-SOE-08-26.