Теорема Рамсея
В комбинаторике теорема Рамсея в одной из своих теоретико-графовых форм утверждает, что можно найти одноцветные клики в любой маркировке ребер (цветами) достаточно большого полного графа . Чтобы продемонстрировать теорему для двух цветов (скажем, синего и красного), пусть r и s будут любыми двумя положительными целыми числами . [a] Теорема Рамсея утверждает, что существует наименьшее положительное целое число R ( r , s ), для которого каждая сине-красная раскраска ребер полного графа на R ( r , s ) вершинах содержит синюю клику на r вершинах или красную клику на s вершинах. (Здесь R ( r , s ) обозначает целое число, которое зависит как от r , так и от s .)
Теорема Рамсея является основополагающим результатом в комбинаторике. Первая версия этого результата была доказана Фрэнком Рамсеем . Это положило начало комбинаторной теории, которая теперь называется теорией Рамсея и ищет регулярность среди беспорядка: общие условия для существования подструктур с регулярными свойствами. В этом приложении речь идет о существовании монохроматических подмножеств , то есть подмножеств связанных ребер только одного цвета.
Расширение этой теоремы применимо к любому конечному числу цветов, а не только к двум. Точнее, теорема утверждает, что для любого заданного числа цветов c и любых заданных целых чисел n 1 , …, n c существует число R ( n 1 , …, n c ) такое, что если ребра полного графа порядка R ( n 1 , …, n c ) раскрашены в c различных цветов, то для некоторого i между 1 и c он должен содержать полный подграф порядка n i , все ребра которого имеют цвет i . В частном случае выше c = 2 (и n 1 = r и n 2 = s ).
Примеры
Р(3, 3) = 6

Из-за принципа ящика, есть по крайней мере 3 ребра одного цвета (пунктирный фиолетовый) из произвольной вершины v . Называя 3 вершины, заканчивающие эти ребра x , y и z , если ребро xy , yz или zx (сплошной черный) имело этот цвет, это завершило бы треугольник с v . Но если нет, каждое должно быть противоположно окрашено, завершая треугольник xyz этого цвета.
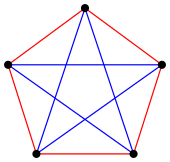
Предположим, что ребра полного графа на 6 вершинах окрашены в красный и синий цвета. Выберите вершину v . Имеется 5 ребер, инцидентных v , и поэтому (по принципу ящика ) по крайней мере 3 из них должны быть одного цвета. Без потери общности мы можем предположить, что по крайней мере 3 из этих ребер, соединяющих вершину v с вершинами r , s и t , являются синими. (Если нет, поменяйте местами красный и синий в дальнейшем.) Если какие-либо из ребер, ( rs ) , ( rt ) , ( st ) , также являются синими, то мы имеем полностью синий треугольник. Если нет, то все эти три ребра красные, и мы имеем полностью красный треугольник. Поскольку это рассуждение работает для любой раскраски, любой K 6 содержит одноцветный K 3 , и поэтому R (3, 3) ≤ 6 . Популярная версия этого называется теоремой о друзьях и незнакомцах .
Альтернативное доказательство работает с помощью двойного подсчета . Оно выглядит следующим образом: подсчитайте количество упорядоченных троек вершин x , y , z , таких, что ребро ( xy ) красное, а ребро ( yz ) синее. Во-первых, любая заданная вершина будет серединой либо 0 × 5 = 0 (все ребра из вершины одного цвета), 1 × 4 = 4 (четыре одного цвета, одно другого цвета) или 2 × 3 = 6 (три одного цвета, два другого цвета) таких троек. Следовательно, существует не более 6 × 6 = 36 таких троек. Во-вторых, для любого неодноцветного треугольника ( xyz ) существует ровно две такие тройки. Следовательно, существует не более 18 неодноцветных треугольников. Следовательно, по крайней мере 2 из 20 треугольников в K 6 являются одноцветными.
Наоборот, можно раскрасить K 5 в 2 цвета , не создавая ни одного монохромного K 3 , показывая, что R (3, 3) > 5 . Уникальная раскраска [b] показана справа. Таким образом, R (3, 3) = 6 .
Задача доказательства того, что R (3, 3) ≤ 6, была одной из задач математического конкурса Уильяма Лоуэлла Патнэма в 1953 году, а также Венгерской математической олимпиады в 1947 году.
Многоцветный пример:Р(3, 3, 3) = 17
Многоцветное число Рамсея — это число Рамсея, использующее 3 или более цветов. Существует (с точностью до симметрии) только два нетривиальных многоцветных числа Рамсея, для которых известно точное значение, а именно R (3, 3, 3) = 17 и R (3, 3, 4) = 30. [ 1]
Предположим, что у нас есть раскраска ребер полного графа с использованием 3 цветов: красного, зеленого и синего. Предположим далее, что раскраска ребер не имеет одноцветных треугольников. Выберите вершину v . Рассмотрим множество вершин, имеющих красное ребро к вершине v . Это называется красной окрестностью v . Красная окрестность v не может содержать никаких красных ребер, так как в противном случае был бы красный треугольник, состоящий из двух конечных точек этого красного ребра и вершины v . Таким образом, индуцированная раскраска ребер в красной окрестности v имеет ребра, окрашенные только в два цвета, а именно в зеленый и синий. Поскольку R (3, 3) = 6 , красная окрестность v может содержать не более 5 вершин. Аналогично зеленая и синяя окрестности v могут содержать не более 5 вершин каждая. Поскольку каждая вершина, за исключением самой v , находится в одной из красных, зеленых или синих окрестностей v , весь полный граф может иметь не более 1 + 5 + 5 + 5 = 16 вершин. Таким образом, мы имеем R (3, 3, 3) ≤ 17 .
Чтобы увидеть, что R (3, 3, 3) = 17 , достаточно нарисовать раскраску рёбер на полном графе с 16 вершинами в 3 цвета, которая избегает одноцветных треугольников. Оказывается, что существует ровно две таких раскраски на K 16 , так называемые нескрученная и скрученная раскраски. Обе раскраски показаны на рисунках справа, с нескрученной раскраской слева, а скрученной справа.
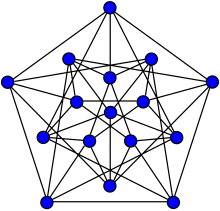
Если мы выберем любой цвет из нескрученной или скрученной раскраски на K 16 и рассмотрим граф, ребра которого — это именно те ребра, которые имеют указанный цвет, мы получим граф Клебша .
Известно, что существует ровно две раскраски рёбер тремя цветами на K 15 , которые избегают одноцветных треугольников, и которые можно построить, удалив любую вершину из нескрученной и скрученной раскраски на K 16 соответственно.
Известно также, что существует ровно 115 раскрасок ребер тремя цветами на квадрате K 14 , которые позволяют избежать одноцветных треугольников, при условии, что мы считаем раскраски ребер, отличающиеся перестановкой цветов, одинаковыми.
Доказательство
2-цветный корпус
Теорема для случая 2 цветов может быть доказана индукцией по r + s . [2] Из определения ясно, что для всех n , R ( n , 2) = R (2, n ) = n . Это начинает индукцию. Мы доказываем, что R ( r , s ) существует, находя для него явную границу. По индуктивному предположению R ( r − 1, s ) и R ( r , s − 1) существуют.
- Лемма 1.
Доказательство. Рассмотрим полный граф на R ( r − 1, s ) + R ( r , s − 1) вершинах, ребра которого раскрашены в два цвета. Выберите вершину v из графа и разбейте оставшиеся вершины на два множества M и N , так что для каждой вершины w , w принадлежит M , если ребро ( vw ) синее, и w принадлежит N , если ( vw ) красное. Поскольку граф имеет вершины, следует, что либо , либо В первом случае, если M имеет красный K s , то и исходный граф тоже, и мы закончили. В противном случае M имеет синий K r − 1 и, следовательно, имеет синий K r по определению M . Последний случай аналогичен. Таким образом, утверждение верно, и мы завершили доказательство для 2 цветов.
В этом двухцветном случае, если R ( r − 1, s ) и R ( r , s − 1) оба четные, неравенство индукции можно усилить до: [3]
Доказательство . Предположим, что p = R ( r − 1, s ) и q = R ( r , s − 1) оба четные. Пусть t = p + q − 1 и рассмотрим двухцветный граф из t вершин. Если d i — степень i -й вершины в синем подграфе, то по лемме о рукопожатии , четно. Учитывая, что t нечетно, должно быть четное d i . Предположим без потери общности, что d 1 четно, а M и N — вершины, инцидентные вершине 1 в синем и красном подграфах соответственно. Тогда и четны. По принципу Пиджеонхола либо либо Поскольку четно, а p – 1 нечетно, первое неравенство можно усилить, так что либо либо Предположим, Тогда либо подграф M имеет красный K s и доказательство завершено, либо он имеет синий K r – 1 , который вместе с вершиной 1 составляет синий K r . Случай рассматривается аналогично.
Корпус большего количества цветов
Лемма 2. Если c > 2 , то
Доказательство. Рассмотрим полный граф вершин и раскрасим его ребра в c цветов. Теперь «становимся дальтониками» и притворимся, что c − 1 и c имеют один и тот же цвет. Таким образом, граф теперь ( c − 1) -цветный. В силу определения такого графа содержит либо K n i , монохромно раскрашенный в цвет i для некоторого 1 ≤ i ≤ c − 2, либо K R ( n c − 1 , n c ) -цветный в «размытый цвет». В первом случае мы закончили. Во втором случае мы снова прозреваем и видим из определения R ( n c − 1 , n c ) , что у нас должен быть либо ( c − 1) -монохромный K n c − 1 , либо c -монохромный K n c . В любом случае доказательство завершено.
Из леммы 1 следует, что любое R ( r , s ) конечно. Правая часть неравенства в лемме 2 выражает число Рамсея для c цветов через числа Рамсея для меньшего числа цветов. Следовательно, любое R ( n 1 , …, n c ) конечно для любого числа цветов. Это доказывает теорему.
числа Рамсея
Числа R ( r , s ) в теореме Рамсея (и их расширения на более чем два цвета) известны как числа Рамсея. Число Рамсея R ( m , n ) дает решение задачи о вечеринке, в которой спрашивается минимальное количество гостей R ( m , n ) , которых нужно пригласить, чтобы по крайней мере m знали друг друга или по крайней мере n не знали друг друга. На языке теории графов число Рамсея — это минимальное количество вершин v = R ( m , n ) , такое, что все неориентированные простые графы порядка v содержат клику порядка m или независимое множество порядка n . Теорема Рамсея утверждает, что такое число существует для всех m и n .
По симметрии верно, что R ( m , n ) = R ( n , m ) . Верхняя граница для R ( r , s ) может быть извлечена из доказательства теоремы, а другие аргументы дают нижние границы. (Первая экспоненциальная нижняя граница была получена Полом Эрдёшем с использованием вероятностного метода .) Однако существует огромный разрыв между самыми точными нижними границами и самыми точными верхними границами. Существует также очень мало чисел r и s , для которых мы знаем точное значение R ( r , s ) .
Вычисление нижней границы L для R ( r , s ) обычно требует демонстрации синей/красной раскраски графа K L −1 без синего подграфа K r и красного подграфа K s . Такой контрпример называется графом Рамсея . Брендан Маккей ведет список известных графов Рамсея. [4] Верхние границы часто значительно сложнее установить: нужно либо проверить все возможные раскраски, чтобы подтвердить отсутствие контрпримера, либо представить математический аргумент в пользу его отсутствия.
Сложность вычислений
Эрдёш просит нас представить себе инопланетную силу, намного более могущественную, чем мы, приземлившуюся на Земле и требующую значение R (5, 5), иначе они уничтожат нашу планету. В этом случае, утверждает он, мы должны мобилизовать все наши компьютеры и всех наших математиков и попытаться найти значение. Но предположим, что вместо этого они просят R (6, 6) . В этом случае, считает он, мы должны попытаться уничтожить инопланетян. [5]
Сложной компьютерной программе не нужно просматривать все раскраски по отдельности, чтобы исключить их все; тем не менее, это очень сложная вычислительная задача, с которой существующее программное обеспечение может справиться только на небольших размерах. Каждый полный граф K n имеет 1/2 n ( n − 1) ребер, поэтому в общей сложности будет c n ( n -1)/2 графов для поиска (для c цветов), если использовать грубую силу. [6] Таким образом, сложность поиска всех возможных графов (с помощью грубой силы ) составляет O ( c n 2 ) для c раскрасок и не более чем n узлов.
Ситуация вряд ли улучшится с появлением квантовых компьютеров . Один из самых известных алгоритмов поиска неструктурированных наборов данных демонстрирует только квадратичное ускорение (ср. алгоритм Гровера ) по сравнению с классическими компьютерами, так что время вычислений по-прежнему экспоненциально зависит от числа узлов. [7] [8]
Известные значения
Как описано выше, R (3, 3) = 6. Легко доказать, что R (4, 2) = 4 , и, в более общем смысле, что R ( s , 2) = s для всех s : граф на s − 1 узлах со всеми ребрами, окрашенными в красный цвет, служит контрпримером и доказывает, что R ( s , 2) ≥ s ; среди раскрасок графа на s узлах раскраска со всеми ребрами, окрашенными в красный цвет, содержит красный подграф с s узлами, а все другие раскраски содержат синий подграф с 2 узлами (то есть пару узлов, соединенных синим ребром).
Используя неравенства индукции и лемму о рукопожатии , можно заключить, что R (4, 3) ≤ R (4, 2) + R (3, 3) − 1 = 9 , и, следовательно, R (4, 4) ≤ R (4, 3) + R (3, 4) ≤ 18. Существует только два графа (4, 4, 16) (то есть 2-раскраски полного графа на 16 узлах без 4-узловых красных или синих полных подграфов) среди 6,4 × 1022 различных 2-раскрасок 16-узловых графов, и только один граф (4, 4, 17) ( граф Пейли порядка 17) среди 2,46 × 1026 раскрасок. [4] Из этого следует, что R (4, 4) = 18 .
Тот факт, что R (4, 5) = 25, был впервые установлен Бренданом Маккеем и Станиславом Радзишовским в 1995 году. [9]
Точное значение R (5, 5) неизвестно, хотя известно, что оно лежит в диапазоне от 43 (Джеффри Эксу (1989) [10] ) до 46 (Ангельтвейт и Маккей (2024) [11] ) включительно.
В 1997 году Маккей, Радзишовски и Эксу использовали методы компьютерной генерации графов, чтобы предположить, что R (5, 5) = 43. Они смогли построить ровно 656 (5, 5, 42) графов, придя к одному и тому же набору графов разными путями. Ни один из 656 графов не может быть расширен до графа (5, 5, 43) . [12]
Для R ( r , s ) с r , s > 5 доступны только слабые границы. Нижние границы для R (6, 6) и R (8, 8) не были улучшены с 1965 и 1972 годов соответственно. [1]
R ( r , s ) при r , s ≤ 10 показаны в таблице ниже. Если точное значение неизвестно, в таблице перечислены наиболее известные границы. R ( r , s ) при r < 3 задаются как R (1, s ) = 1 и R (2, s ) = s для всех значений s .
The standard survey on the development of Ramsey number research is the Dynamic Survey 1 of the Electronic Journal of Combinatorics, by Stanisław Radziszowski, which is periodically updated.[1][13] Where not cited otherwise, entries in the table below are taken from the June 2024 edition. (Note there is a trivial symmetry across the diagonal since R(r, s) = R(s, r).)
s r | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 3 | 6 | 9 | 14 | 18 | 23 | 28 | 36 | 40–41[14] | ||
| 4 | 18 | 25[9] | 36–40 | 49–58 | 59[15]–79 | 73–105 | 92–135 | |||
| 5 | 43–46[11] | 59[16]–85 | 80–133 | 101–193 | 133–282 | 149[15]–381 | ||||
| 6 | 102–160 | 115[15]–270 | 134[15]–423 | 183–651 | 204–944 | |||||
| 7 | 205–492 | 219–832 | 252–1368 | 292–2119 | ||||||
| 8 | 282–1518 | 329–2662 | 343–4402 | |||||||
| 9 | 565–4956 | 581–8675 | ||||||||
| 10 | 798–16064 |
Asymptotics
The inequality R(r, s) ≤ R(r − 1, s) + R(r, s − 1) may be applied inductively to prove that
In particular, this result, due to Erdős and Szekeres, implies that when r = s,
An exponential lower bound,
was given by Erdős in 1947 and was instrumental in his introduction of the probabilistic method. There is a huge gap between these two bounds: for example, for s = 10, this gives 101 ≤ R(10, 10) ≤ 48,620. Nevertheless, the exponential growth factors of either bound were not improved for a long time, and for the lower bound it still stands at √2. There is no known explicit construction producing an exponential lower bound. The best known lower and upper bounds for diagonal Ramsey numbers are
due to Spencer and Conlon, respectively; a 2023 preprint by Campos, Griffiths, Morris and Sahasrabudhe claims to have made exponential progress using an algorithmic construction relying on a graph structure called a "book",[17][18] improving the upper bound to
with and where it is believed these parameters could be optimized, in particular .
For the off-diagonal Ramsey numbers R(3, t), it is known that they are of order t2/log t; this may be stated equivalently as saying that the smallest possible independence number in an n-vertex triangle-free graph is
The upper bound for R(3, t) is given by Ajtai, Komlós, and Szemerédi,[19] the lower bound was obtained originally by Kim,[20] and the implicit constant was improved independently by Fiz Pontiveros, Griffiths and Morris,[21] and Bohman and Keevash,[22] by analysing the triangle-free process. Furthermore, studying the more general "H-free process" has set the best known asymptotic lower bounds for general off-diagonal Ramsey numbers,[23] R(s, t)
For the bounds become , but a 2023 preprint[24][25] has improved the lower bound to which settles a question of Erdős who offered 250 dollars for a proof that the lower limit has form .[26][27]
Formal verification of Ramsey numbers
The Ramsey number has been formally verified to be 28.[28] This verification was achieved using a combination of Boolean satisfiability (SAT) solving and computer algebra systems (CAS). The proof was generated automatically using the SAT+CAS approach, marking the first certifiable proof of . The verification process required 96 hours of computation on a high-performance processor, producing a 30 GB DRAT (Deletion Resolution Asymmetric Tautology) file. This file was independently verified using the DRAT-trim proof checker in 63 hours.
The Ramsey number has been formally verified to be 25.[29] The original proof, developed by McKay and Radziszowski in 1995, combined high-level mathematical arguments with computational steps and used multiple independent implementations to reduce the possibility of programming errors. This new formal proof was carried out using the HOL4 interactive theorem prover, limiting the potential for errors to the HOL4 kernel. Rather than directly verifying the original algorithms, the authors utilized HOL4's interface to the MiniSat SAT solver to formally prove key gluing lemmas.
Induced Ramsey
There is a less well-known yet interesting analogue of Ramsey's theorem for induced subgraphs. Roughly speaking, instead of finding a monochromatic subgraph, we are now required to find a monochromatic induced subgraph. In this variant, it is no longer sufficient to restrict our focus to complete graphs, since the existence of a complete subgraph does not imply the existence of an induced subgraph. The qualitative statement of the theorem in the next section was first proven independently by Erdős, Hajnal and Pósa, Deuber and Rödl in the 1970s.[30][31][32] Since then, there has been much research in obtaining good bounds for induced Ramsey numbers.
Statement
Let H be a graph on n vertices. Then, there exists a graph G such that any coloring of the edges of G using two colors contains a monochromatic induced copy of H (i.e. an induced subgraph of G such that it is isomorphic to H and its edges are monochromatic). The smallest possible number of vertices of G is the induced Ramsey number rind(H).
Sometimes, we also consider the asymmetric version of the problem. We define rind(X,Y) to be the smallest possible number of vertices of a graph G such that every coloring of the edges of G using only red or blue contains a red induced subgraph of X or blue induced subgraph of Y.
History and bounds
Similar to Ramsey's theorem, it is unclear a priori whether induced Ramsey numbers exist for every graph H. In the early 1970s, Erdős, Hajnal and Pósa, Deuber and Rödl independently proved that this is the case.[30][31][32] However, the original proofs gave terrible bounds (e.g. towers of twos) on the induced Ramsey numbers. It is interesting to ask if better bounds can be achieved. In 1974, Paul Erdős conjectured that there exists a constant c such that every graph H on k vertices satisfies rind(H) ≤ 2ck.[33] If this conjecture is true, it would be optimal up to the constant c because the complete graph achieves a lower bound of this form (in fact, it's the same as Ramsey numbers). However, this conjecture is still open as of now.
In 1984, Erdős and Hajnal claimed that they proved the bound[34]
However, that was still far from the exponential bound conjectured by Erdős. It was not until 1998 when a major breakthrough was achieved by Kohayakawa, Prömel and Rödl, who proved the first almost-exponential bound of rind(H) ≤ 2ck(log k)2 for some constant c. Their approach was to consider a suitable random graph constructed on projective planes and show that it has the desired properties with nonzero probability. The idea of using random graphs on projective planes have also previously been used in studying Ramsey properties with respect to vertex colorings and the induced Ramsey problem on bounded degree graphs H.[35]
Kohayakawa, Prömel and Rödl's bound remained the best general bound for a decade. In 2008, Fox and Sudakov provided an explicit construction for induced Ramsey numbers with the same bound.[36] In fact, they showed that every (n,d,λ)-graph G with small λ and suitable d contains an induced monochromatic copy of any graph on k vertices in any coloring of edges of G in two colors. In particular, for some constant c, the Paley graph on n ≥ 2ck log2k vertices is such that all of its edge colorings in two colors contain an induced monochromatic copy of every k-vertex graph.
In 2010, Conlon, Fox and Sudakov were able to improve the bound to rind(H) ≤ 2ck log k, which remains the current best upper bound for general induced Ramsey numbers.[37] Similar to the previous work in 2008, they showed that every (n,d,λ)-graph G with small λ and edge density 1⁄2 contains an induced monochromatic copy of every graph on k vertices in any edge coloring in two colors. Currently, Erdős's conjecture that rind(H) ≤ 2ck remains open and is one of the important problems in extremal graph theory.
For lower bounds, not much is known in general except for the fact that induced Ramsey numbers must be at least the corresponding Ramsey numbers. Some lower bounds have been obtained for some special cases (see Special Cases).
Special cases
While the general bounds for the induced Ramsey numbers are exponential in the size of the graph, the behaviour is much different on special classes of graphs (in particular, sparse ones). Many of these classes have induced Ramsey numbers polynomial in the number of vertices.
If H is a cycle, path or star on k vertices, it is known that rind(H) is linear in k.[36]
If H is a tree on k vertices, it is known that rind(H) = O(k2 log2k).[38] It is also known that rind(H) is superlinear (i.e. rind(H) = ω(k)). Note that this is in contrast to the usual Ramsey numbers, where the Burr–Erdős conjecture (now proven) tells us that r(H) is linear (since trees are 1-degenerate).
For graphs H with number of vertices k and bounded degree Δ, it was conjectured that rind(H) ≤ cnd(Δ), for some constant d depending only on Δ. This result was first proven by Łuczak and Rödl in 1996, with d(Δ) growing as a tower of twos with height O(Δ2).[39] More reasonable bounds for d(Δ) were obtained since then. In 2013, Conlon, Fox and Zhao showed using a counting lemma for sparse pseudorandom graphs that rind(H) ≤ cn2Δ+8, where the exponent is best possible up to constant factors.[40]
Generalizations
Similar to Ramsey numbers, we can generalize the notion of induced Ramsey numbers to hypergraphs and multicolor settings.
More colors
We can also generalize the induced Ramsey's theorem to a multicolor setting. For graphs H1, H2, …, Hr, define rind(H1, H2, …, Hr) to be the minimum number of vertices in a graph G such that any coloring of the edges of G into r colors contain an induced subgraph isomorphic to Hi where all edges are colored in the i-th color for some 1 ≤ i ≤ r. Let rind(H;q) := rind(H, H, …, H) (q copies of H).
It is possible to derive a bound on rind(H;q) which is approximately a tower of two of height ~ log q by iteratively applying the bound on the two-color case. The current best known bound is due to Fox and Sudakov, which achieves rind(H;q) ≤ 2ck3, where k is the number of vertices of H and c is a constant depending only on q.[41]
Hypergraphs
We can extend the definition of induced Ramsey numbers to d-uniform hypergraphs by simply changing the word graph in the statement to hypergraph. Furthermore, we can define the multicolor version of induced Ramsey numbers in the same way as the previous subsection.
Let H be a d-uniform hypergraph with k vertices. Define the tower function tr(x) by letting t1(x) = x and for i ≥ 1, ti+1(x) = 2ti(x). Using the hypergraph container method, Conlon, Dellamonica, La Fleur, Rödl and Schacht were able to show that for d ≥ 3, q ≥ 2, rind(H;q) ≤ td(ck) for some constant c depending on only d and q. In particular, this result mirrors the best known bound for the usual Ramsey number when d = 3.[42]
Extensions of the theorem
Infinite graphs
A further result, also commonly called Ramsey's theorem, applies to infinite graphs. In a context where finite graphs are also being discussed it is often called the "Infinite Ramsey theorem". As intuition provided by the pictorial representation of a graph is diminished when moving from finite to infinite graphs, theorems in this area are usually phrased in set-theoretic terminology.[43]
- Theorem. Let be some infinite set and colour the elements of (the subsets of of size ) in different colours. Then there exists some infinite subset of such that the size subsets of all have the same colour.
Proof: The proof is by induction on n, the size of the subsets. For n = 1, the statement is equivalent to saying that if you split an infinite set into a finite number of sets, then one of them is infinite. This is evident. Assuming the theorem is true for n ≤ r, we prove it for n = r + 1. Given a c-colouring of the (r + 1)-element subsets of X, let a0 be an element of X and let Y = X \ {a0}. We then induce a c-colouring of the r-element subsets of Y, by just adding a0 to each r-element subset (to get an (r + 1)-element subset of X). By the induction hypothesis, there exists an infinite subset Y1 of Y such that every r-element subset of Y1 is coloured the same colour in the induced colouring. Thus there is an element a0 and an infinite subset Y1 such that all the (r + 1)-element subsets of X consisting of a0 and r elements of Y1 have the same colour. By the same argument, there is an element a1 in Y1 and an infinite subset Y2 of Y1 with the same properties. Inductively, we obtain a sequence {a0, a1, a2, …} such that the colour of each (r + 1)-element subset (ai(1), ai(2), …, ai(r + 1)) with i(1) < i(2) < … < i(r + 1) depends only on the value of i(1). Further, there are infinitely many values of i(n) such that this colour will be the same. Take these ai(n)'s to get the desired monochromatic set.
A stronger but unbalanced infinite form of Ramsey's theorem for graphs, the Erdős–Dushnik–Miller theorem, states that every infinite graph contains either a countably infinite independent set, or an infinite clique of the same cardinality as the original graph.[44]
Infinite version implies the finite
It is possible to deduce the finite Ramsey theorem from the infinite version by a proof by contradiction. Suppose the finite Ramsey theorem is false. Then there exist integers c, n, T such that for every integer k, there exists a c-colouring of [k](n) without a monochromatic set of size T. Let Ck denote the c-colourings of [k](n) without a monochromatic set of size T.
For any k, the restriction of a colouring in Ck+1 to [k](n) (by ignoring the colour of all sets containing k + 1) is a colouring in Ck. Define to be the colourings in Ck which are restrictions of colourings in Ck+1. Since Ck+1 is not empty, neither is .
Similarly, the restriction of any colouring in is in , allowing one to define as the set of all such restrictions, a non-empty set. Continuing so, define for all integers m, k.
Now, for any integer k,
and each set is non-empty. Furthermore, Ck is finite as
It follows that the intersection of all of these sets is non-empty, and let
Then every colouring in Dk is the restriction of a colouring in Dk+1. Therefore, by unrestricting a colouring in Dk to a colouring in Dk+1, and continuing doing so, one constructs a colouring of without any monochromatic set of size T. This contradicts the infinite Ramsey theorem.
If a suitable topological viewpoint is taken, this argument becomes a standard compactness argument showing that the infinite version of the theorem implies the finite version.[45]
Hypergraphs
The theorem can also be extended to hypergraphs. An m-hypergraph is a graph whose "edges" are sets of m vertices – in a normal graph an edge is a set of 2 vertices. The full statement of Ramsey's theorem for hypergraphs is that for any integers m and c, and any integers n1, …, nc, there is an integer R(n1, …, nc; m) such that if the hyperedges of a complete m-hypergraph of order R(n1, …, nc; m) are coloured with c different colours, then for some i between 1 and c, the hypergraph must contain a complete sub-m-hypergraph of order ni whose hyperedges are all colour i. This theorem is usually proved by induction on m, the 'hyper-ness' of the graph. The base case for the proof is m = 2, which is exactly the theorem above.
For m = 3 we know the exact value of one non-trivial Ramsey number, namely R(4, 4; 3) = 13. This fact was established by Brendan McKay and Stanisław Radziszowski in 1991.[46] Additionally, we have: R(4, 5; 3) ≥ 35,[47] R(4, 6; 3) ≥ 63 and R(5, 5; 3) ≥ 88.[47]
Directed graphs
It is also possible to define Ramsey numbers for directed graphs; these were introduced by P. Erdős and L. Moser (1964). Let R(n) be the smallest number Q such that any complete graph with singly directed arcs (also called a "tournament") and with ≥ Q nodes contains an acyclic (also called "transitive") n-node subtournament.
This is the directed-graph analogue of what (above) has been called R(n, n; 2), the smallest number Z such that any 2-colouring of the edges of a complete undirected graph with ≥ Z nodes, contains a monochromatic complete graph on n nodes. (The directed analogue of the two possible arc colours is the two directions of the arcs, the analogue of "monochromatic" is "all arc-arrows point the same way"; i.e., "acyclic.")
We have R(0) = 0, R(1) = 1, R(2) = 2, R(3) = 4, R(4) = 8, R(5) = 14, R(6) = 28, and 34 ≤ R(7) ≤ 47.[48][49]
Uncountable cardinals
In terms of the partition calculus, Ramsey's theorem can be stated as for all finite n and k. Wacław Sierpiński showed that the Ramsey theorem does not extend to graphs of size by showing that . In particular, the continuum hypothesis implies that . Stevo Todorčević showed that in fact in ZFC, , a much stronger statement than . Justin T. Moore has strengthened this result further. On the positive side, a Ramsey cardinal, , is a large cardinal axiomatically defined to satisfy the related formula: . The existence of Ramsey cardinals cannot be proved in ZFC.
Relationship to the axiom of choice
In reverse mathematics, there is a significant difference in proof strength between the version of Ramsey's theorem for infinite graphs (the case n = 2) and for infinite multigraphs (the case n ≥ 3). The multigraph version of the theorem is equivalent in strength to the arithmetical comprehension axiom, making it part of the subsystem ACA0 of second-order arithmetic, one of the big five subsystems in reverse mathematics. In contrast, by a theorem of David Seetapun, the graph version of the theorem is weaker than ACA0, and (combining Seetapun's result with others) it does not fall into one of the big five subsystems.[50] Over ZF, however, the graph version implies the classical Kőnig's lemma, whereas the converse implication does not hold,[51] since Kőnig's lemma is equivalent to countable choice from finite sets in this setting.[52]
See also
- Ramsey cardinal
- Paris–Harrington theorem
- Sim (pencil game)
- Infinite Ramsey theory
- Van der Waerden number
- Ramsey game
- Erdős–Rado theorem
Notes
- ^ Some authors restrict the values to be greater than one, for example (Brualdi 2010) and (Harary 1972), thus avoiding a discussion of edge colouring a graph with no edges, while others rephrase the statement of the theorem to require, in a simple graph, either an r-clique or an s-independent set, see (Gross 2008) or (Erdős & Szekeres 1935). In this form, the consideration of graphs with one vertex is more natural.
- ^ Up to automorphisms of the graph.
- ^ a b c Radziszowski, Stanisław (2011). "Small Ramsey Numbers". Dynamic Surveys. Electronic Journal of Combinatorics. 1000. doi:10.37236/21.
- ^ Do, Norman (2006). "Party problems and Ramsey theory" (PDF). Austr. Math. Soc. Gazette. 33 (5): 306–312.
- ^ "Party Acquaintances".
- ^ a b "Ramsey Graphs".
- ^ Joel H. Spencer (1994), Ten Lectures on the Probabilistic Method, SIAM, p. 4, ISBN 978-0-89871-325-1
- ^ 2.6 Ramsey Theory from Mathematics Illuminated
- ^ Montanaro, Ashley (2016). "Quantum algorithms: an overview". npj Quantum Information. 2 (1): 15023. arXiv:1511.04206. Bibcode:2016npjQI...215023M. doi:10.1038/npjqi.2015.23. S2CID 2992738 – via Nature.
- ^ Wang, Hefeng (2016). "Determining Ramsey numbers on a quantum computer". Physical Review A. 93 (3): 032301. arXiv:1510.01884. Bibcode:2016PhRvA..93c2301W. doi:10.1103/PhysRevA.93.032301. S2CID 118724989.
- ^ a b McKay, Brendan D.; Radziszowski, Stanislaw P. (May 1995). "R(4,5) = 25" (PDF). Journal of Graph Theory. 19 (3): 309–322. doi:10.1002/jgt.3190190304.
- ^ Exoo, Geoffrey (March 1989). "A lower bound for R(5, 5)". Journal of Graph Theory. 13 (1): 97–98. doi:10.1002/jgt.3190130113.
- ^ a b Vigleik Angeltveit; Brendan McKay (September 2024). "". arXiv:2409.15709 [math.CO].
- ^ Brendan D. McKay, Stanisław P. Radziszowski (1997). "Subgraph Counting Identities and Ramsey Numbers" (PDF). Journal of Combinatorial Theory. Series B. 69 (2): 193–209. doi:10.1006/jctb.1996.1741.
- ^ Stanisław Radziszowski. "DS1". Retrieved 17 August 2023.
- ^ Angeltveit, Vigleik (31 Dec 2023). "". arXiv:2401.00392 [math.CO].
- ^ a b c d Exoo, Geoffrey; Tatarevic, Milos (2015). "New Lower Bounds for 28 Classical Ramsey Numbers". Electronic Journal of Combinatorics. 22 (3): 3. arXiv:1504.02403. Bibcode:2015arXiv150402403E. doi:10.37236/5254.
- ^ Exoo, Geoffrey (26 Oct 2023). "A Lower Bound for R(5,6)". arXiv:2310.17099 [math.CO].
- ^ Campos, Marcelo; Griffiths, Simon; Morris, Robert; Sahasrabudhe, Julian (2023). "An exponential improvement for diagonal Ramsey". arXiv:2303.09521 [math.CO].
- ^ Sloman, Leila (2 May 2023). "A Very Big Small Leap Forward in Graph Theory". Quanta Magazine.
- ^ Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1980-11-01). "A note on Ramsey numbers". Journal of Combinatorial Theory, Series A. 29 (3): 354–360. doi:10.1016/0097-3165(80)90030-8. ISSN 0097-3165.
- ^ Kim, Jeong Han (1995), "The Ramsey Number R(3,t) has order of magnitude t2/log t", Random Structures and Algorithms, 7 (3): 173–207, CiteSeerX 10.1.1.46.5058, doi:10.1002/rsa.3240070302
- ^ "The Triangle-Free Process and the Ramsey Number R(3,k)". bookstore.ams.org. Retrieved 2023-06-27.
- ^ Bohman, Tom; Keevash, Peter (2020-11-17). "Dynamic concentration of the triangle-free process". Random Structures and Algorithms. 58 (2): 221–293. arXiv:1302.5963. doi:10.1002/rsa.20973.
- ^ Bohman, Tom; Keevash, Peter (2010-08-01). "The early evolution of the H-free process". Inventiones Mathematicae. 181 (2): 291–336. arXiv:0908.0429. Bibcode:2010InMat.181..291B. doi:10.1007/s00222-010-0247-x. ISSN 1432-1297.
- ^ Mattheus, Sam; Verstraete, Jacques (5 Mar 2024). "The asymptotics of r(4,t)". Annals of Mathematics. 199 (2). arXiv:2306.04007. doi:10.4007/annals.2024.199.2.8.
- ^ Cepelewicz, Jordana (22 June 2023). "Mathematicians Discover Novel Way to Predict Structure in Graphs". Quanta Magazine.
- ^ Erdös, Paul (1990), Nešetřil, Jaroslav; Rödl, Vojtěch (eds.), "Problems and Results on Graphs and Hypergraphs: Similarities and Differences", Mathematics of Ramsey Theory, Algorithms and Combinatorics, vol. 5, Berlin, Heidelberg: Springer, pp. 12–28, doi:10.1007/978-3-642-72905-8_2, ISBN 978-3-642-72905-8, retrieved 2023-06-27
- ^ "Erdős Problems". www.erdosproblems.com. Retrieved 2023-07-12.
- ^ Duggan, Conor; Li, Zhengyu; Bright, Curtis; Ganesh, Vijay (2024), "A SAT+ Computer Algebra System Verification of the Ramsey Problem R(3,8) (Student Abstract)", Proceedings of the AAAI Conference on Artificial Intelligence, vol. 38, no. 21, pp. 23480–23481
- ^ Gauthier, Thibault; Brown, Chad E (2024), "A formal proof of R(4,5)=25", arXiv preprint, arXiv:2404.01761
- ^ a b Erdős, P.; Hajnal, A.; Pósa, L. (1975). "Strong embeddings of graphs into colored graphs". Infinite and Finite Sets, Vol. 1. Colloquia Mathematica Societatis János Bolyai. Vol. 10. North-Holland, Amsterdam/London. pp. 585–595.
- ^ a b Deuber, W. (1975). "A generalization of Ramsey's theorem". Infinite and Finite Sets, Vol. 1. Colloquia Mathematica Societatis János Bolyai. Vol. 10. North-Holland, Amsterdam/London. pp. 323–332.
- ^ a b Rödl, V. (1973). The dimension of a graph and generalized Ramsey theorems (Master's thesis). Charles University.
- ^ Erdős, P. (1975). "Problems and results on finite and infinite graphs". Recent advances in graph theory (Proceedings of the Second Czechoslovak Symposium, Prague, 1974). Academia, Prague. pp. 183–192.
- ^ Erdős, Paul (1984). "On some problems in graph theory, combinatorial analysis and combinatorial number theory" (PDF). Graph Theory and Combinatorics: 1–17.
- ^ Kohayakawa, Y.; Prömel, H.J.; Rödl, V. (1998). "Induced Ramsey Numbers" (PDF). Combinatorica. 18 (3): 373–404. doi:10.1007/PL00009828.
- ^ a b Fox, Jacob; Sudakov, Benny (2008). "Induced Ramsey-type theorems". Advances in Mathematics. 219 (6): 1771–1800. arXiv:0706.4112. doi:10.1016/j.aim.2008.07.009.
- ^ Conlon, David; Fox, Jacob; Sudakov, Benny (2012). "On two problems in graph Ramsey theory". Combinatorica. 32 (5): 513–535. arXiv:1002.0045. doi:10.1007/s00493-012-2710-3.
- ^ Beck, József (1990). "On Size Ramsey Number of Paths, Trees and Circuits. II". In Nešetřil, J.; Rödl, V. (eds.). Mathematics of Ramsey Theory. Algorithms and Combinatorics. Vol. 5. Springer, Berlin, Heidelberg. pp. 34–45. doi:10.1007/978-3-642-72905-8_4. ISBN 978-3-642-72907-2.
- ^ Łuczak, Tomasz; Rödl, Vojtěch (March 1996). "On induced Ramsey numbers for graphs with bounded maximum degree". Journal of Combinatorial Theory. Series B. 66 (2): 324–333. doi:10.1006/jctb.1996.0025.
- ^ Conlon, David; Fox, Jacob; Zhao, Yufei (May 2014). "Extremal results in sparse pseudorandom graphs". Advances in Mathematics. 256: 206–29. arXiv:1204.6645. doi:10.1016/j.aim.2013.12.004.
- ^ Fox, Jacob; Sudakov, Benny (2009). "Density theorems for bipartite graphs and related Ramsey-type results". Combinatorica. 29 (2): 153–196. arXiv:0707.4159v2. doi:10.1007/s00493-009-2475-5.
- ^ Conlon, David; Dellamonica Jr., Domingos; La Fleur, Steven; Rödl, Vojtěch; Schacht, Mathias (2017). "A note on induced Ramsey numbers". In Loebl, Martin; Nešetřil, Jaroslav; Thomas, Robin (eds.). A Journey Through Discrete Mathematics. Springer, Cham. pp. 357–366. arXiv:1601.01493. doi:10.1007/978-3-319-44479-6_13. ISBN 978-3-319-44478-9.
- ^ Gould, Martin. "Ramsey Theory" (PDF). Mathematical Institute, University of Oxford. Archived from the original (PDF) on 2022-01-30.
- ^ Dushnik, Ben; Miller, E. W. (1941). "Partially ordered sets". American Journal of Mathematics. 63 (3): 600–610. doi:10.2307/2371374. hdl:10338.dmlcz/100377. JSTOR 2371374. MR 0004862.. See in particular Theorems 5.22 and 5.23.
- ^ Diestel, Reinhard (2010). "Chapter 8, Infinite Graphs". Graph Theory (4 ed.). Heidelberg: Springer-Verlag. pp. 209–2010. ISBN 978-3-662-53621-6.
- ^ McKay, Brendan D.; Radziszowski, Stanislaw P. (1991). "The First Classical Ramsey Number for Hypergraphs is Computed". Proceedings of the Second Annual ACM-SIAM Symposium on Discrete Algorithms, SODA'91: 304–308.
- ^ a b Dybizbański, Janusz (2018-12-31). "A lower bound on the hypergraph Ramsey number R(4,5;3)". Contributions to Discrete Mathematics. 13 (2). doi:10.11575/cdm.v13i2.62416. ISSN 1715-0868.
- ^ Smith, Warren D.; Exoo, Geoff, Partial Answer to Puzzle #27: A Ramsey-like quantity, retrieved 2020-06-02
- ^ Neiman, David; Mackey, John; Heule, Marijn (2020-11-01). "Tighter Bounds on Directed Ramsey Number R(7)". arXiv:2011.00683 [math.CO].
- ^ Hirschfeldt, Denis R. (2014). Slicing the Truth. Lecture Notes Series of the Institute for Mathematical Sciences, National University of Singapore. Vol. 28. World Scientific.
- ^ Blass, Andreas (September 1977). "Ramsey's theorem in the hierarchy of choice principles". The Journal of Symbolic Logic. 42 (3): 387–390. doi:10.2307/2272866. ISSN 1943-5886. JSTOR 2272866.
- ^ Forster, T.E.; Truss, J.K. (January 2007). "Ramsey's theorem and König's Lemma". Archive for Mathematical Logic. 46 (1): 37–42. doi:10.1007/s00153-006-0025-z. ISSN 1432-0665.
References
- Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1980), "A note on Ramsey numbers", J. Combin. Theory Ser. A, 29 (3): 354–360, doi:10.1016/0097-3165(80)90030-8.
- Bohman, Tom; Keevash, Peter (2010), "The early evolution of the H-free process", Invent. Math., 181 (2): 291–336, arXiv:0908.0429, Bibcode:2010InMat.181..291B, doi:10.1007/s00222-010-0247-x, S2CID 2429894
- Brualdi, Richard A. (2010), Introductory Combinatorics (5th ed.), Prentice-Hall, pp. 77–82, ISBN 978-0-13-602040-0
- Conlon, David (2009), "A new upper bound for diagonal Ramsey numbers", Annals of Mathematics, 170 (2): 941–960, arXiv:math/0607788v1, doi:10.4007/annals.2009.170.941, MR 2552114, S2CID 9238219.
- Erdős, Paul (1947), "Some remarks on the theory of graphs", Bull. Amer. Math. Soc., 53 (4): 292–294, doi:10.1090/S0002-9904-1947-08785-1.
- Erdős, P.; Moser, L. (1964), "On the representation of directed graphs as unions of orderings" (PDF), A Magyar Tudományos Akadémia, Matematikai Kutató Intézetének Közleményei, 9: 125–132, MR 0168494
- Erdős, Paul; Szekeres, George (1935), "A combinatorial problem in geometry" (PDF), Compositio Mathematica, 2: 463–470, doi:10.1007/978-0-8176-4842-8_3, ISBN 978-0-8176-4841-1.
- Exoo, G. (1989), "A lower bound for R(5,5)", Journal of Graph Theory, 13: 97–98, doi:10.1002/jgt.3190130113.
- Graham, R.; Rothschild, B.; Spencer, J. H. (1990), Ramsey Theory, New York: John Wiley and Sons.
- Gross, Jonathan L. (2008), Combinatorial Methods with Computer Applications, CRC Press, p. 458, ISBN 978-1-58488-743-0
- Harary, Frank (1972), Graph Theory, Addison-Wesley, pp. 16–17, ISBN 0-201-02787-9
- Ramsey, F. P. (1930), "On a problem of formal logic", Proceedings of the London Mathematical Society, 30: 264–286, doi:10.1112/plms/s2-30.1.264.
- Spencer, J. (1975), "Ramsey's theorem – a new lower bound", J. Combin. Theory Ser. A, 18: 108–115, doi:10.1016/0097-3165(75)90071-0.
- Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank (2013), "Experimental determination of Ramsey numbers", Physical Review Letters, 111 (13): 130505, arXiv:1201.1842, Bibcode:2013PhRvL.111m0505B, doi:10.1103/PhysRevLett.111.130505, PMID 24116761, S2CID 1303361.
External links
- "Ramsey theorem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Ramsey@Home is a distributed computing project designed to find new lower bounds for various Ramsey numbers using a host of different techniques.
- The Electronic Journal of Combinatorics dynamic survey of small Ramsey numbers (by Stanisław Radziszowski)
- Ramsey Number – from MathWorld (contains lower and upper bounds up to R(19, 19))
- Ramsey Number – Geoffrey Exoo (Contains R(5, 5) > 42 counter-proof)





















![{\displaystyle [1+o(1)]{\frac {{\sqrt {2}}s}{e}}2^{\frac {s}{2}}\leq R(s,s)\leq s^{-(c\log s)/(\log \log s)}4^{s},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98d3d42edf70185ccfa40a6b0153b034f595e9e1)















![{\displaystyle [X]^{n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eba2dbab7c22faa180f674d89ae74d3f2a778337)















![{\displaystyle \aleph _{1}\nrightarrow [\aleph _{1}]_{\aleph _{1}}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ecac308e6d102699ff81ec9d125bed772486ae6)




