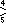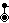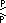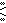Квазиправильный многогранник
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В геометрии квазиправильный многогранник — это однородный многогранник , имеющий ровно два вида правильных граней , которые чередуются вокруг каждой вершины . Они являются вершинно-транзитивными и рёберно-транзитивными , следовательно, на шаг ближе к правильным многогранникам , чем полуправильные , которые являются просто вершинно-транзитивными.
Их двойственные фигуры являются гранно-транзитивными и рёберно-транзитивными; они имеют ровно два вида правильных вершинных фигур , которые чередуются вокруг каждой грани . Иногда их также считают квазиправильными.
Существует только два выпуклых квазиправильных многогранника: кубооктаэдр и икосододекаэдр . Их названия, данные Кеплером , происходят от признания того, что их грани являются всеми гранями (повернутыми по-разному) парного куба и октаэдра в первом случае и парного икосаэдра и додекаэдра во втором случае.
Этим формам, представляющим пару правильной фигуры и ее двойственной фигуры, можно присвоить вертикальный символ Шлефли или r{p,q} , чтобы обозначить, что их грани являются всеми гранями (повернутыми по-разному) как правильной {p,q} , так и двойственной правильной {q,p} . Квазиправильный многогранник с этим символом будет иметь конфигурацию вершин p.qpq (или (pq) 2 ).
В более общем случае квазиправильная фигура может иметь конфигурацию вершины (pq) r , представляющую собой r (2 или более) последовательностей граней вокруг вершины.
Мозаики плоскости также могут быть квазирегулярными, в частности, тригексагональная мозаика с конфигурацией вершин (3.6) 2 . Другие квазирегулярные мозаики существуют на гиперболической плоскости, например, тригептагональная мозаика , (3.7) 2 . Или, в более общем случае: (pq) 2 , с 1/p + 1/q < 1/2 .
Правильные многогранники и мозаики с четным числом граней в каждой вершине также можно считать квазиправильными, различая грани одного порядка, представляя их по-разному, например, раскрашивая их попеременно (без определения какой-либо ориентации поверхности). Правильную фигуру с символом Шлефли {p,q} можно считать квазиправильной с конфигурацией вершин (pp) q/2 , если q четно.
Примеры:
Правильный октаэдр с символом Шлефли {3,4} и четным числом 4 можно считать квазиправильным как тетратетраэдр (2 набора по 4 треугольника тетраэдра ) с конфигурацией вершин (3.3) 4/2 = (3 a .3 b ) 2 , чередующим два цвета треугольных граней.
Квадратную мозаику с конфигурацией вершин 4 4 и 4 четными числами можно считать квазиправильной с конфигурацией вершин (4.4) 4/2 = (4 a .4 b ) 2 , раскрашенной в шахматном порядке .
Треугольную мозаику с четной конфигурацией вершин 3 6 и 6 можно считать квазиправильной с конфигурацией вершин (3.3) 6/2 = (3 a .3 b ) 3 , чередующей два цвета треугольных граней.
Строительство Витхофф
 Правильные ( p | 2 q ) и квазиправильные многогранники ( 2 | pq ) создаются с помощью конструкции Витхоффа с точкой-генератором в одном из 3 углов фундаментальной области. Это определяет одно ребро внутри фундаментальной области. |
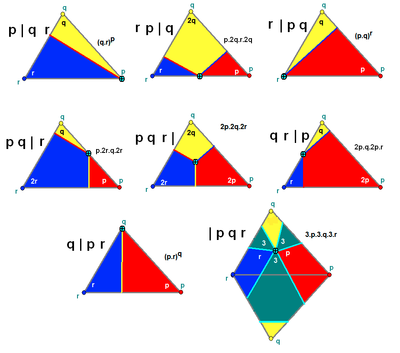
q | 2 p , p | 2 q , 2 | pq
Коксетер определяет квазиправильный многогранник как имеющий символ Витхоффа в форме p | qr , и он является правильным, если q=2 или q=r. [1]
Диаграмма Коксетера-Дынкина — это еще одно символическое представление, показывающее квазирегулярное отношение между двумя дуально-регулярными формами:
| Символ Шлефли | Диаграмма Коксетера | Символ Витхоффа | |
|---|---|---|---|
| {п,д} |      | д | 2 п | |
| {д,п} |      | п | 2 д | |
| г{п,д} |      или или 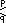  | 2 | пк | |
Выпуклые квазиправильные многогранники
Существуют два однородных выпуклых квазиправильных многогранника:
- Кубооктаэдр , конфигурация вершины (3.4) 2 , диаграмма Коксетера- Дынкина





- Икосододекаэдр , конфигурация вершин (3.5) 2 , диаграмма Коксетера - Дынкина





Кроме того, октаэдр , который также является правильным , , конфигурация вершин (3.3) 2 , может считаться квазиправильным, если чередующимся граням приданы разные цвета. В этой форме его иногда называют тетратетраэдром . Остальные выпуклые правильные многогранники имеют нечетное число граней в каждой вершине, поэтому не могут быть окрашены таким образом, чтобы сохранить транзитивность ребер. Он имеет диаграмму Коксетера-Дынкина 




Каждый из них образует общее ядро двойственной пары правильных многогранников . Названия двух из них дают ключ к соответствующей двойственной паре: соответственно кубооктаэдр и икосаэдр додекаэдр . Октаэдр является общим ядром двойственной пары тетраэдров (соединение, известное как звездчатая октаэдрическая форма ); когда он получен таким образом, октаэдр иногда называют тетратетраэдром , как тетраэдр тетраэдр .
| Обычный | Двойной регулярный | Квазирегулярное общее ядро | Вершинная фигура |
|---|---|---|---|
 Тетраэдр {3,3}      3 | 2 3 |  Тетраэдр {3,3}      3 | 2 3 |  Тетратетраэдр r{3,3}      2 | 3 3 |  3.3.3.3 |
 Куб {4,3}      3 | 2 4 |  Октаэдр {3,4}      4 | 2 3 |  Кубооктаэдр r{3,4}      2 | 3 4 |  3.4.3.4 |
 Додекаэдр {5,3}      3 | 2 5 |  Икосаэдр {3,5}      5 | 2 3 |  Икосододекаэдр r{3,5}      2 | 3 5 |  3.5.3.5 |
Каждый из этих квазиправильных многогранников может быть построен с помощью операции ректификации любого из правильных родительских многогранников, полностью усекая вершины, пока каждое исходное ребро не сведется к своей средней точке.
Квазирегулярные мозаики
Эта последовательность продолжается как тригексагональная мозаика , вершинная фигура (3.6) 2 - квазиправильная мозаика , основанная на треугольной мозаике и шестиугольной мозаике .
| Обычный | Двойной регулярный | Квазирегулярная комбинация | Вершинная фигура |
|---|---|---|---|
 Шестиугольная мозаика {6,3}      6 | 2 3 |  Треугольная мозаика {3,6}      3 | 2 6 |  Тригексагональная мозаика r{6,3}      2 | 3 6 |  (3,6) 2 |
Узор шахматной доски — это квазирегулярная раскраска квадратной мозаики , вершинная фигура (4.4) 2 :
| Обычный | Двойной регулярный | Квазирегулярная комбинация | Вершинная фигура |
|---|---|---|---|
 {4,4}      4 | 2 4 |  {4,4}      4 | 2 4 |  г{4,4}      2 | 4 4 |  (4.4) 2 |
Треугольную мозаику также можно считать квазиправильной, с тремя наборами чередующихся треугольников в каждой вершине, (3.3) 3 :
 ч{6,3} 3 | 3 3    = =     |
На гиперболической плоскости эта последовательность продолжается дальше, например, тригептагональная мозаика , вершинная фигура (3.7) 2 - квазиправильная мозаика, основанная на треугольной мозаике порядка 7 и семиугольной мозаике .
| Обычный | Двойной регулярный | Квазирегулярная комбинация | Вершинная фигура |
|---|---|---|---|
 Семиугольная мозаика {7,3}      7 | 2 3 |  Треугольная мозаика {3,7}      3 | 2 7 |  Тригептагональная мозаика r{3,7}      2 | 3 7 |  (3,7) 2 |
Невыпуклые примеры
Коксетер, Х.С.М. и др. (1954) также классифицируют некоторые звездчатые многогранники , имеющие те же характеристики, как квазиправильные.
Два из них основаны на двойственных парах правильных тел Кеплера–Пуансо , так же, как и для выпуклых примеров:
большой икосододекаэдр и додекододекаэдр :
| Обычный | Двойной регулярный | Квазирегулярное общее ядро | Вершинная фигура |
|---|---|---|---|
 Большой звездчатый додекаэдр { 5 / 2 ,3}        3 | 2 5/2 |  Большой икосаэдр {3, 5 / 2 }        5/2 | 2 3 |  Большой икосододекаэдр r{3, 5 / 2 }        2 | 3 5/2 |  3. 5 / 2 .3. 5 / 2 |
 Малый звездчатый додекаэдр { 5 / 2 ,5}        5 | 2 5/2 |  Большой додекаэдр {5, 5 / 2 }        5/2 | 2 5 |  Додекадодекаэдр r{5, 5 / 2 }        2 | 5 5/2 |  5. 5 / 2 .5. 5 / 2 |
Еще девять — это полумногогранники , которые являются гранеными формами вышеупомянутых квазиправильных многогранников, полученных путем ректификации правильных многогранников. Они включают экваториальные грани, проходящие через центр многогранников:
| Квазирегулярный (выпрямленный) |  Тетратетраэдр |  Кубооктаэдр |  Икосододекаэдр |  Большой икосододекаэдр |  Додекадодекаэдр |
|---|---|---|---|---|---|
| Квазиправильные (гемимногогранники) |  Тетрагемигексаэдр 3 / 2 3 | 2 |  Октагемиоктаэдр 3 / 2 3 | 3 |  Малый икосигемидодекаэдр 3 / 2 3 | 5 |  Большой икосигемидодекаэдр 3 / 2 3 | 5 / 3 |  Малый додекагемикосаэдр 5 / 3 5 / 2 | 3 |
| Вершинная фигура |  3.4.3 / 2 .4 |  3.6.3 / 2 .6 |  3.10.3 / 2 .10 |  3. 10 / 3 . 3 / 2 . 10 / 3 |  5 / 2 .6. 5 / 3 .6 |
| Квазиправильные (гемимногогранники) |  Кубогемиоктаэдр 4 / 3 4 | 3 |  Малый додекагемидодекаэдр 5 / 4 5 | 5 |  Большой додекагемидодекаэдр 5 / 3 5 / 2 | 5 / 3 |  Большой додекагемикосаэдр 5 / 4 5 | 3 | |
| Вершинная фигура |  4.6.4 / 3 .6 |  5.10.5 / 4 .10 |  5/2 . 10 / 3 . 5 / 3 . 10 / 3 |  5.6.5 / 4 .6 |
Наконец, существуют три дитригональные формы, все из которых являются гранями правильного додекаэдра, вершинные фигуры которого содержат три чередования двух типов граней:
| Изображение | Граненая форма символа Витхоффа Диаграмма Коксетера | Вершинная фигура |
|---|---|---|
 | Дитригональный додекадодекаэдр 3 | 5/3 5  или или   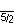  |  (5.5/3) 3 |
 | Малый дитригональный икосододекаэдр 3 | 5/2 3 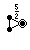 или или     | 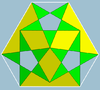 (3.5/2) 3 |
 | Большой дитригональный икосододекаэдр 3/2 | 3 5 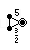 или или 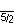    |  ((3,5) 3 )/2 |
На евклидовой плоскости последовательность полумногогранников продолжается следующими четырьмя звездными мозаиками, где апейрогоны появляются как вышеупомянутые экваториальные многоугольники:
Квазирегулярные дуальные
Некоторые авторитеты утверждают, что, поскольку двойственные квазирегулярным телам обладают теми же симметриями, эти двойственные тела также следует называть квазирегулярными. Но не все используют эту терминологию. Эти двойственные тела транзитивны на своих ребрах и гранях (но не на своих вершинах); они являются транзитивными по ребрам каталонскими телами . Выпуклые тела, в соответствующем порядке, как указано выше:
- Ромбический додекаэдр с двумя типами чередующихся вершин: 8 с тремя ромбическими гранями и 6 с четырьмя ромбическими гранями.
- Ромбический триаконтаэдр с двумя типами чередующихся вершин: 20 с тремя ромбическими гранями и 12 с пятью ромбическими гранями.
Кроме того, по двойственности с октаэдром куб , который обычно является правильным , можно сделать квазиправильным, если придать его чередующимся вершинам разные цвета.
Их конфигурации лица имеют вид V3.n.3.n, а диаграмма Коксетера-Дынкина 




 |  |  |  |  |  |
| Куб V(3.3) 2      | Ромбический додекаэдр V(3,4) 2      | Ромбический триаконтаэдр V(3,5) 2      | Ромбическая мозаика V(3.6) 2      | В(3,7) 2     | В(3,8) 2     |
Эти три квазирегулярных дуальных многогранника также характеризуются наличием ромбических граней.
Этот узор с ромбическими гранями продолжается как V(3.6) 2 , ромбическая мозаика .
Квазиправильные многогранники и соты
В более высоких измерениях Коксетер определил квазирегулярный многогранник или соту, имеющую регулярные грани и квазирегулярные вершинные фигуры. Из этого следует, что все вершинные фигуры конгруэнтны и что существует два вида граней, которые чередуются. [2]
В евклидовом 4-мерном пространстве правильный 16-ячейник также можно рассматривать как квазиправильный, как чередующийся тессеракт , h{4,3,3}, диаграммы Коксетера :





 =
=



 , состоящий из чередующихся тетраэдров и тетраэдрических ячеек . Его вершинная фигура — квазиправильный тетратетраэдр (октаэдр с тетраэдрической симметрией),
, состоящий из чередующихся тетраэдров и тетраэдрических ячеек . Его вершинная фигура — квазиправильный тетратетраэдр (октаэдр с тетраэдрической симметрией),



 .
.
Единственные квазирегулярные соты в евклидовом 3-мерном пространстве — это чередующиеся кубические соты , h{4,3,4}, диаграммы Коксетера:





 =
=



 , составленный из чередующихся тетраэдрических и октаэдрических ячеек . Его вершинная фигура — квазиправильный кубооктаэдр ,
, составленный из чередующихся тетраэдрических и октаэдрических ячеек . Его вершинная фигура — квазиправильный кубооктаэдр ,



 . [2]
. [2]
В гиперболическом 3-мерном пространстве одна квазирегулярная сотовая структура представляет собой чередующиеся кубические соты 5-го порядка , h{4,3,5}, диаграммы Кокстера:





 =
=



 , составленный из чередующихся тетраэдрических и икосаэдрических ячеек . Его вершинная фигура — квазиправильный икосододекаэдр ,
, составленный из чередующихся тетраэдрических и икосаэдрических ячеек . Его вершинная фигура — квазиправильный икосододекаэдр ,



 [3] Связанная паракомпактная чередующаяся кубическая сота порядка 6 , h{4,3,6} имеет чередующиеся тетраэдрические и шестиугольные ячейки мозаики с вершинной фигурой, является квазиправильной тригексагональной мозаикой ,
[3] Связанная паракомпактная чередующаяся кубическая сота порядка 6 , h{4,3,6} имеет чередующиеся тетраэдрические и шестиугольные ячейки мозаики с вершинной фигурой, является квазиправильной тригексагональной мозаикой ,



 .
.
| Квазирегулярные полихоры и соты: h{4,p,q} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Космос | Конечный | Аффинный | Компактный | Паракомпактный | |||||||
Символ Шлефли | ч{4,3,3} | ч{4,3,4} | ч{4,3,5} | ч{4,3,6} | ч{4,4,3} | ч{4,4,4} | |||||
Диаграмма Коксетера |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     |        ↔ ↔     | |||||
     ↔ ↔       |    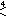  |      |      |      |      ↔ ↔       | ||||||
| Изображение |  |  |  |  | |||||||
| Вершинная фигура r{p,3} |       |       |       |       |       |       | |||||
Правильные полихоры или соты формы {p,3,4} или





 можно уменьшить симметрию вдвое, как
можно уменьшить симметрию вдвое, как





 в квазирегулярную форму
в квазирегулярную форму



 , создавая попеременно окрашенные ячейки {p,3}. Эти случаи включают евклидовы кубические соты {4,3,4} с кубическими ячейками, и компактные гиперболические {5,3,4} с додекаэдрическими ячейками, и паракомпактные {6,3,4} с бесконечными шестиугольными ячейками мозаики. Они имеют четыре ячейки вокруг каждого ребра, чередующиеся в 2 цветах. Их вершинные фигуры — квазиправильные тетратетраэдры,
, создавая попеременно окрашенные ячейки {p,3}. Эти случаи включают евклидовы кубические соты {4,3,4} с кубическими ячейками, и компактные гиперболические {5,3,4} с додекаэдрическими ячейками, и паракомпактные {6,3,4} с бесконечными шестиугольными ячейками мозаики. Они имеют четыре ячейки вокруг каждого ребра, чередующиеся в 2 цветах. Их вершинные фигуры — квазиправильные тетратетраэдры,



 =
=

 .
.



 , то же, что и правильный октаэдр
, то же, что и правильный октаэдр| Регулярные и квазирегулярные соты: {p,3,4} и {p,3 1,1 } | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Космос | Евклидово 4-мерное пространство | Евклидово 3-пространство | Гиперболическое 3-пространство | ||||||||
| Имя | {3,3,4} {3,3 1,1 } = | {4,3,4} {4,3 1,1 } = | {5,3,4} {5,3 1,1 } = | {6,3,4} {6,3 1,1 } = | |||||||
Диаграмма Коксетера |        = =     |        = =     |        = =     |        = =     | |||||||
| Изображение |  |  |  |  | |||||||
| Клетки {p,3} |       |       |       |       | |||||||
Аналогично правильные гиперболические соты вида {p,3,6} или





 можно уменьшить симметрию вдвое, как
можно уменьшить симметрию вдвое, как





 в квазирегулярную форму
в квазирегулярную форму



 , создавая поочередно окрашенные ячейки {p,3}. Они имеют шесть ячеек вокруг каждого края, поочередно окрашенных в 2 цвета. Их вершинные фигуры — квазиправильные треугольные мозаики ,
, создавая поочередно окрашенные ячейки {p,3}. Они имеют шесть ячеек вокруг каждого края, поочередно окрашенных в 2 цвета. Их вершинные фигуры — квазиправильные треугольные мозаики ,

 .
.





 =
=


| Форма | Паракомпактный | Некомпактный | |||||
|---|---|---|---|---|---|---|---|
| Имя | {3,3,6} {3,3 [3] } | {4,3,6} {4,3 [3] } | {5,3,6} {5,3 [3] } | {6,3,6} {6,3 [3] } | {7,3,6} {7,3 [3] } | {8,3,6} {8,3 [3] } | ... {∞,3,6} {∞,3 [3] } |
            |             |             |             |             |             |             |             |
| Изображение |  |  |  |  |  |  |  |
| Клетки |  {3,3}      |  {4,3}      |  {5,3}      |  {6,3}      |  {7,3}      |  {8,3}      |  {∞,3}      |
Смотрите также
Примечания
- ^ Коксетер, Х. С. М. , Лонге-Хиггинс, М. С. и Миллер, Дж. К. П. Однородные многогранники, Философские труды Лондонского королевского общества 246 A (1954), стр. 401–450. (Раздел 7, Правильные и квазиправильные многогранники p | qr )
- ^ ab Coxeter, Regular Polytopes, 4.7 Другие соты. стр.69, стр.88
- ^ Coxeter, HSM; Whitrow, GJ (26 апреля 1950 г.). «Структура мира и неевклидовы соты». Труды Лондонского королевского общества. Серия A, Математические и физические науки . 201 (1066): 417– 437. doi :10.1098/rspa.1950.0070.
Ссылки
- Кромвель, П. Многогранники , Издательство Кембриджского университета (1977).
- Коксетер , Правильные многогранники , (3-е издание, 1973), издание Дувра, ISBN 0-486-61480-8 , 2.3 Квазиправильные многогранники. (стр. 17), Квазиправильные соты, стр. 69
Внешние ссылки
- Вайсштейн, Эрик В. «Квазиправильный многогранник». Математический мир .
- Вайсштейн, Эрик В. «Однородный многогранник». MathWorld .Квазиправильные многогранники: (pq) r
- Джордж Харт, Квазиправильные многогранники