Квази-расслоение

В алгебраической топологии квазирасслоение является обобщением расслоений и расслоений, введенных Альбрехтом Дольдом и Рене Томом . Грубо говоря, это непрерывное отображение p : E → B, имеющее то же поведение, что и расслоение относительно (относительных) гомотопических групп E , B и p −1 ⁽ x ) . Эквивалентно, можно определить квазирасслоение как непрерывное отображение, такое что включение каждого слоя в его гомотопический слой является слабой эквивалентностью . Одно из основных приложений квазирасслоений заключается в доказательстве теоремы Дольда-Тома .

Непрерывное сюръективное отображение топологических пространств p : E → B называется квазирасслоением , если оно индуцирует изоморфизмы

${\displaystyle p_{*}\colon \пи _{i}(E,p^{-1}(x),y)\to \пи _{i}(B,x)}$

для всех x ∈ B , y ∈ p ⁻¹ ( x ) и i ≥ 0. При i = 0,1 можно говорить только о биекциях между двумя множествами.

По определению, квазирасслоения обладают ключевым свойством расслоений, а именно, что квазирасслоение p : E → B индуцирует длинную точную последовательность гомотопических групп

${\displaystyle {\begin{align}\dots \to \pi _{i+1}(B,x)\to \pi _{i}(p^{-1}(x),y)\to \pi _{i}(E,y)&\to \pi _{i}(B,x)\to \dots \\&\to \pi _{0}(B,x)\to 0\end{align}}}$

как следует непосредственно из длинной точной последовательности для пары ( E , p ⁻¹ ( x )).

Эта длинная точная последовательность также функториальна в следующем смысле: любое послойное отображение f : E → E′ индуцирует морфизм между точными последовательностями пар ( E , p ⁻¹ ( x )) и ( E′ , p′ ⁻¹ ( x )) и, следовательно, морфизм между точными последовательностями квазирасслоения. Следовательно, диаграмма

коммутирует с f _{0 ,} являющимся ограничением f на p ⁻¹ ( x ), и x′ , являющимся элементом формы p′ ( f ( e )) для e ∈ p ⁻¹ ( x ).

Эквивалентное определение гласит, что сюръективное отображение p : E → B является квазирасслоением, если включение слоя p ⁻¹ ( b ) в гомотопический слой F _b отображения p над b является слабой эквивалентностью для всех b ∈ B . Чтобы увидеть это, напомним, что F _b является слоем q относительно b , где q : E _p → B является обычной конструкцией расслоения путей . Таким образом, имеем

${\displaystyle E_{p}=\{(e,\gamma)\in E\times B^{I}:\gamma (0)=p(e)\}}$

и q задается как q ( e , γ) = γ(1). Теперь рассмотрим естественную гомотопическую эквивалентность φ : E → E _p , заданную как φ( e ) = ( e , p ( e )), где p ( e ) обозначает соответствующий постоянный путь. По определению, p пропускается через E _p таким образом, что получается коммутативная диаграмма

Применение π _n дает альтернативное определение.

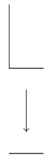
• Каждое расслоение Серра является квазирасслоением. Это следует из свойства подъема гомотопии .
• Проекция буквы L на ее базовый интервал является квазирасслоением, но не расслоением. В более общем смысле, проекция M _f → I цилиндра отображения f : X → Y между связными комплексами CW на единичный интервал является квазирасслоением тогда и только тогда, когда π i ₍ M f _, p −1 ⁽ b ) ) = 0 = π _i ( I , b ) выполняется для всех i ∈ I и b ∈ B . Но по длинной точной последовательности пары ( M _f , p ⁻¹ ( b )) и по теореме Уайтхеда это эквивалентно тому, что f является гомотопической эквивалентностью . Для топологических пространств X и Y в общем случае это эквивалентно тому, что f является слабой гомотопической эквивалентностью. Более того, если f не сюръективно, то непостоянные пути в I , начинающиеся в 0, не могут быть подняты до путей, начинающихся в точке Y вне образа f в M _f . Это означает, что в этом случае проекция не является расслоением.
• Отображение SP( p ) : SP( X ) → SP( X / A ), индуцированное проекцией p : X → X / A , является квазирасслоением для пары CW ( X , A ), состоящей из двух связных пространств. Это одно из основных утверждений, используемых в доказательстве теоремы Дольда-Тома . В общем случае это отображение также не является расслоением.

Следующее является прямым следствием альтернативного определения расслоения с использованием гомотопического слоя:

Теорема. Каждое квазирасслоение p : E → B пропускается через расслоение, слои которого слабо гомотопически эквивалентны слоям p .

Следствием этой теоремы является то, что все слои квазирасслоения слабо гомотопически эквивалентны, если базовое пространство линейно связно , как это имеет место для расслоений.

Проверка того, является ли заданное отображение квазирасслоением, как правило, довольно утомительна. Следующие две теоремы призваны облегчить эту задачу. Они будут использовать следующее понятие: Пусть p : E → B — непрерывное отображение. Подмножество U ⊂ p ( E ) называется выделенным (относительно p ), если p : p ⁻¹ ( U ) → U — квазирасслоение.

Теорема. Если открытые подмножества U,V и U ∩ V различаются относительно непрерывного отображения p : E → B , то также различается и U ∪ V . ^[1]

Теорема. Пусть p : E → B — непрерывное отображение, где B — индуктивный предел последовательности B ₁ ⊂ B ₂ ⊂ ... Более того, предполагается, что все B _n удовлетворяют первой аксиоме разделения. Если все B _n различимы, то p — квазирасслоение.

Чтобы увидеть, что последнее утверждение верно, нужно только иметь в виду, что непрерывные образы компактных множеств в B уже лежат в некотором B _n . Таким образом, можно свести его к случаю, когда утверждение известно. Эти две теоремы означают, что достаточно показать, что заданное отображение является квазирасслоением на определенных подмножествах. Затем можно склеить их вместе, чтобы увидеть, что это справедливо на больших подмножествах, и, наконец, используя предельный аргумент, можно увидеть, что отображение является квазирасслоением на всем пространстве. Эта процедура, например, использовалась в доказательстве теоремы Дольда-Тома.

• Агилар, Марсело; Гитлер, Самуэль; Прието, Карлос (2008). Алгебраическая топология с гомотопической точки зрения . Springer Science & Business Media. ISBN 978-0-387-22489-3.
• Дольд, Альбрехт; Лашоф, Ричард ( 1959 ), «Главные квазирасслоения и гомотопическая эквивалентность расслоений», Illinois Journal of Mathematics , 2 (2): 285–305
• Дольд, Альбрехт; Том, Рене (1958), «Quasifaserungen und unendliche symmetrische Produkte», Annals of Mathematics , Second Series, 67 (2): 239–281 , doi : 10.2307/1970005, ISSN  0003-486X, JSTOR  1970005, MR  0097062
• Хэтчер, Аллен (2002). Алгебраическая топология. Cambridge University Press . ISBN 978-0-521-79540-1.
• Мэй, Дж. Питер (1990), «Слабые эквивалентности и квазирасслоения», Springer Lecture Notes , 1425 : 91–101
• Piccinini, Renzo A. (1992). Лекции по теории гомотопии . Elsevier. ISBN 9780080872827.

• Квазифибрилляции и гомотопические обратные пути на MathOverflow
• Квазифибры от Университета Лехай