Группа квазидиэдра

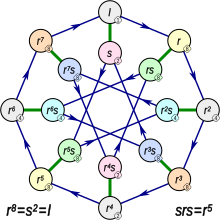
В математике квазидиэдральные группы , также называемые полудиэдральными группами , являются некоторыми неабелевыми группами порядка степени 2. Для каждого положительного целого числа n, большего или равного 4, существует ровно четыре класса изоморфизма неабелевых групп порядка 2 ^{n ,} которые имеют циклическую подгруппу индекса 2. Две из них хорошо известны: обобщенная группа кватернионов и диэдральная группа . Одна из оставшихся двух групп часто считается особенно важной, поскольку она является примером 2-группы максимального класса нильпотентности . В тексте Бертрама Хупперта Endliche Gruppen эта группа называется «Quasidiedergruppe». В тексте Даниэля Горенштейна Finite Groups эта группа называется «полудиэдральной группой». Даммит и Фут называют ее «квазидиэдральной группой»; мы принимаем это название в этой статье. Все дают одну и ту же презентацию для этой группы:

${\displaystyle \langle r,s\mid r^{2^{n-1}}=s^{2}=1, \ srs=r^{2^{n-2}-1}\rangle \, \!}$.

Другая неабелева 2-группа с циклической подгруппой индекса 2 не имеет специального названия ни в одном из текстов, а обозначается просто как G или M _m (2). Когда эта группа имеет порядок 16, Даммит и Фут называют эту группу «модулярной группой порядка 16», поскольку ее решетка подгрупп является модулярной . В этой статье эта группа будет называться модулярной максимальной циклической группой порядка . Ее представление таково:${\displaystyle 2^{n}}$

${\displaystyle \langle r,s\mid r^{2^{n-1}}=s^{2}=1, \ srs=r^{2^{n-2}+1}\rangle \, \!}$.

Обе эти группы и группа диэдра являются полупрямыми произведениями циклической группы < r > порядка 2 ^{n −1} с циклической группой < s > порядка 2. Такое неабелево полупрямое произведение однозначно определяется элементом порядка 2 в группе единиц кольца , и существует ровно три таких элемента, , и , соответствующие группе диэдра, квазидиэдральной и модулярной максимально-циклической группе.${\displaystyle \mathbb {Z} /2^{n-1} \mathbb {Z} }$${\displaystyle 2^{n-1}-1}$${\displaystyle 2^{n-2}-1}$${\displaystyle 2^{n-2}+1}$

Обобщенная группа кватернионов, диэдральная группа и квазидиэдральная группа порядка 2 ⁿ имеют класс нильпотентности n − 1 и являются единственными классами изоморфизма групп порядка 2 ⁿ с классом нильпотентности n − 1. Группы порядка p ⁿ и класса нильпотентности n − 1 были началом классификации всех p -групп через кокласс . Модулярная максимально-циклическая группа порядка 2 ⁿ всегда имеет класс нильпотентности 2. Это делает модулярную максимально-циклическую группу менее интересной, поскольку большинство групп порядка p ⁿ для больших n имеют класс нильпотентности 2 и оказались сложными для непосредственного понимания.

Обобщенный кватернион, диэдральная и квазидиэдральная группы являются единственными 2-группами, производная подгруппа которых имеет индекс 4. Теорема Альперина–Брауэра–Горенштейна классифицирует простые группы и, в некоторой степени , конечные группы с квазидиэдральными силовскими 2-подгруппами.

Силовские 2-подгруппы следующих групп являются квазидиэдральными:

• PSL ₃ ( F _q ) для q ≡ 3 mod 4,
• PSU ₃ ( F _q ) для q ≡ 1 mod 4,
• Группа Матье М ₁₁ ,
• GL ₂ ( F _q ) для q ≡ 3 mod 4.

• Даммит, Д.С.; Фут, Р. (2004). Абстрактная алгебра (3-е изд.). Wiley. стр.  71–72 . ISBN 9780471433347.
• Юпперт, Б. (1967). Эндличе Группен . Спрингер. С.  90–93 . МР  0224703.
• Горенштейн, Д. (1980). Конечные группы . Челси. С.  188–195 . ISBN 0-8284-0301-5. МР  0569209.