Проекция (математика)

Отображение равно его площади под композицией отображения

В математике проекция — это идемпотентное отображение множества (или другой математической структуры ) в подмножество (или подструктуру). В этом случае идемпотентность означает, что проецирование дважды равнозначно проецированию один раз. Ограничение на подпространство проекции также называется проекцией , даже если свойство идемпотентности теряется. Повседневным примером проекции является отбрасывание тени на плоскость (лист бумаги): проекция точки — это ее тень на листе бумаги, а проекция (тень) точки на листе бумаги — это сама эта точка (идемпотентность). Тень трехмерной сферы — это диск. Первоначально понятие проекции было введено в евклидовой геометрии для обозначения проекции трехмерного евклидова пространства на плоскость в нем, как в примере с тенью. Две основные проекции такого рода:

Проекция из точки на плоскость или центральная проекция : Если $C$ — точка, называемая центром проекции , то проекция точки $P,$ отличной от $C,$ на плоскость, не содержащую $C,$ является пересечением прямой CP $с$ плоскостью. Точки $P,$ такие, что прямая $CP$ параллельна плоскости , не имеют никакого изображения при проекции, но часто говорят, что они проецируются в точку, находящуюся в бесконечности плоскости (формализацию этой терминологии см. в Проективной геометрии ). Проекция самой точки $C$ не определена.
Проекция , параллельная направлению $D$ , на плоскость или параллельная проекция : Изображение точки $P$ является пересечением плоскости с прямой, параллельной $D$ , проходящей через $P.$ См. Аффинное пространство § Проекция для точного определения, обобщенного на любое измерение. ^{[ необходима ссылка ]}

Концепция проекции в математике очень старая и, скорее всего, берет свое начало в явлении теней, отбрасываемых реальными объектами на землю. Эта элементарная идея была уточнена и абстрагирована, сначала в геометрическом контексте, а затем в других разделах математики. Со временем развивались различные версии этой концепции, но сегодня, в достаточно абстрактной обстановке, мы можем объединить эти вариации. ^{[ необходима цитата ]}

В картографии проекция карты — это отображение части поверхности Земли на плоскость, которая в некоторых случаях, но не всегда, является ограничением проекции в указанном выше значении. 3D-проекции также лежат в основе теории перспективы . ^{[ требуется цитата ]}

Необходимость объединения двух видов проекций и определения изображения центральной проекцией любой точки, отличной от центра проекции, лежит в основе проективной геометрии .

Определение

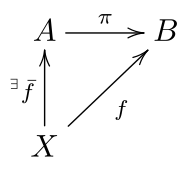
Коммутативность этой диаграммы заключается в универсальности проекции $π$ для любого отображения $f$ и множества $X.$

В общем случае отображение, в котором область и область значений являются одним и тем же множеством (или математической структурой ), является проекцией, если отображение идемпотентно , что означает, что проекция равна своей композиции с собой. Проекция может также относиться к отображению, которое имеет правое обратное . Оба понятия тесно связаны следующим образом. Пусть $p$ — идемпотентное отображение из множества $A$ в себя (таким образом, $p \circ p = p$ ), а $B = p (A)$ — образ $p$ . Если мы обозначим через $π$ отображение $p,$ рассматриваемое как отображение из $A$ на $B$ , а через $i —$ инъекцию B в A $($ так что $p$ $=$ $i$ $\circ$ $π$ ), то мы имеем $π$ $\circ$ $i$ $= Id$ $B$ (так что $π имеет$ $правое$ обратное). Наоборот, если $π$ имеет правый обратный $i$ , то $π$ $\circ$ $i$ $= Id$ $B$ подразумевает, что $i$ $\circ$ $π$ $\circ$ $i$ $\circ$ $π$ $=$ $i$ $\circ Id$ $B$ $\circ$ $π$ $=$ $i$ $\circ$ $π$ ; то есть $p$ $=$ $i$ $\circ$ $π$ является идемпотентом. ^[^{требуется ссылка}^]

Приложения

Первоначальное понятие проекции было расширено или обобщено на различные математические ситуации, часто, но не всегда, связанные с геометрией, например:

В теории множеств :
- Операция, характеризуемая $j$ - ^й проекцией , обозначаемая $proj j$ , которая переводит элемент $x = (x 1, ..., x j, ..., x n)$ декартова произведения $X 1 \times \dots \times X j \times \dots \times X n$ в значение $proj j (x) = x j .$ ^[1] Это отображение всегда сюръективно , и когда каждое пространство $X k$ имеет топологию , это отображение также непрерывно и открыто . ^[2]
- Отображение, которое переводит элемент в его класс эквивалентности при заданном отношении эквивалентности, называется канонической проекцией . ^[3]
- Карта оценки отправляет функцию $f$ к значению $f (x)$ для фиксированного $x$ . Пространство функций $Y X$ можно отождествить с декартовым произведением , а карта оценки является проекционной картой из декартового произведения. ^[^{необходима цитата}^] ${\textstyle \prod _{i\in X}Y}$
Для реляционных баз данных и языков запросов проекция представляет собой унарную операцию, записанную как , где — набор имен атрибутов. Результат такой проекции определяется как набор , который получается, когда все кортежи в $R$ ограничиваются набором . ^[4]^[5]^[6]^[^{требуется проверка}^] $R$ — это отношение базы данных . ^[^{требуется цитата}^] $\Pi _{a_{1},\ldots ,a_{n}}(R)$ $a_{1},\ldots ,a_{n}$ $\{a_{1},\ldots ,a_{n}\}$
В сферической геометрии проекция сферы на плоскость использовалась Птолемеем (~150) в его Planisphaerium . ^[7] Метод называется стереографической проекцией и использует плоскость, касательную к сфере, и полюс C, диаметрально противоположный точке касания. Любая точка $P$ на сфере, кроме $C,$ определяет прямую $CP$ , пересекающую плоскость в проецируемой точке для $P.$ ^[8] Соответствие делает сферу одноточечной компактификацией для плоскости, когда включена точка на бесконечности, соответствующая $C$ , которая в противном случае не имеет проекции на плоскость. Обычным примером является комплексная плоскость , где компактификация соответствует сфере Римана . В качестве альтернативы, полусфера часто проецируется на плоскость с использованием гномонической проекции . ^{[ требуется ссылка ]}
В линейной алгебре — линейное преобразование , которое остается неизменным, если применяется дважды: $p (u) = p (p (u))$ . Другими словами, идемпотентный оператор. Например, отображение, которое переводит точку $(x, y, z)$ в трех измерениях в точку $(x, y, 0),$ является проекцией. Этот тип проекции естественным образом обобщается на любое число измерений $n$ для области и $k \leq n$ для области определения отображения. См. Ортогональная проекция , Проекция (линейная алгебра) . В случае ортогональных проекций пространство допускает разложение в виде произведения, и оператор проекции также является проекцией в этом смысле. ^[9]^[10]^{[ требуется проверка ]}
В дифференциальной топологии любое расслоение волокон включает проекционную карту как часть своего определения. Локально, по крайней мере, эта карта выглядит как проекционная карта в смысле топологии продукта и, следовательно, открыта и сюръективна. ^{[ необходима цитата ]}
В топологии ретракция — это непрерывное отображение $r$ $:$ $X$ $\to$ $X$ , которое ограничивается тождественным отображением на своем образе. ^[11] Это удовлетворяет аналогичному условию идемпотентности $r$ $2$ $=$ $r$ и может считаться обобщением проекционного отображения. Изображение ретракции называется ретрактом исходного пространства. Ретракция, гомотопная тождеству , известна как деформационная ретракция . Этот термин также используется в теории категорий для обозначения любого расщепленного эпиморфизма. ^[^{необходима цитата}^]
Скалярная проекция (или резольвента) одного вектора на другой.
В теории категорий указанное выше понятие декартова произведения множеств может быть обобщено на произвольные категории. Произведение некоторых объектов имеет канонический морфизм проекции на каждый фактор. Особые случаи включают проекцию из декартова произведения множеств , топологию произведения топологических пространств ( которая всегда сюръективна и открыта ) или из прямого произведения групп и т. д. Хотя эти морфизмы часто являются эпиморфизмами и даже сюръективны, они не обязаны быть таковыми. ^[12][ ^{требуется}^{проверка}^]

Ссылки

^ "Прямой продукт - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .
^ Ли, Джон М. (2012). Введение в гладкие многообразия. Graduate Texts in Mathematics. Том 218 (Второе изд.). С. 606. doi :10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5. Упражнение A.32. Предположим, что — топологические пространства. Покажите, что каждая проекция — открытое отображение. $X_{1},\ldots ,X_{k}$ $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$
^ Браун, Арлен; Пирси, Карл (1994-12-16). Введение в анализ. Springer Science & Business Media. ISBN 978-0-387-94369-5.
^ Alagic, Suad (2012-12-06). Технология реляционных баз данных. Springer Science & Business Media. ISBN 978-1-4612-4922-1.
^ Дата, CJ (2006-08-28). Словарь реляционных баз данных: полный глоссарий реляционных терминов и концепций с иллюстративными примерами. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.
^ "Relational Algebra". www.cs.rochester.edu . Архивировано из оригинала 30 января 2004 года . Получено 29 августа 2021 года .
^ Сидоли, Натан; Берггрен, Дж. Л. (2007). «Арабская версия Птолемеевской планисферы или уплощение поверхности сферы: текст, перевод, комментарий» (PDF) . Sciamvs . 8 . Получено 11 августа 2021 г. .
^ "Стереографическая проекция - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .
^ "Проекция - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .
^ Роман, Стивен (2007-09-20). Продвинутая линейная алгебра. Springer Science & Business Media. ISBN 978-0-387-72831-5.
^ "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org . Получено 2021-08-11 .
^ "Произведение семейства объектов в категории - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .

Дальнейшее чтение

Томас Крейг (1882) Трактат о проекциях из коллекции исторической математики Мичиганского университета .

[1] "Прямой продукт - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .

[2] Ли, Джон М. (2012). Введение в гладкие многообразия. Graduate Texts in Mathematics. Том 218 (Второе изд.). С. 606. doi :10.1007/978-1-4419-9982-5. ISBN 978-1-4419-9982-5. Упражнение A.32. Предположим, что — топологические пространства. Покажите, что каждая проекция — открытое отображение. $X_{1},\ldots ,X_{k}$ $\pi _{i}:X_{1}\times \cdots \times X_{k}\to X_{i}$

[3] Браун, Арлен; Пирси, Карл (1994-12-16). Введение в анализ. Springer Science & Business Media. ISBN 978-0-387-94369-5.

[4] Alagic, Suad (2012-12-06). Технология реляционных баз данных. Springer Science & Business Media. ISBN 978-1-4612-4922-1.

[5] Дата, CJ (2006-08-28). Словарь реляционных баз данных: полный глоссарий реляционных терминов и концепций с иллюстративными примерами. "O'Reilly Media, Inc.". ISBN 978-1-4493-9115-7.

[6] "Relational Algebra". www.cs.rochester.edu . Архивировано из оригинала 30 января 2004 года . Получено 29 августа 2021 года .

[7] Сидоли, Натан; Берггрен, Дж. Л. (2007). «Арабская версия Птолемеевской планисферы или уплощение поверхности сферы: текст, перевод, комментарий» (PDF) . Sciamvs . 8 . Получено 11 августа 2021 г. .

[8] "Стереографическая проекция - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .

[9] "Проекция - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .

[10] Роман, Стивен (2007-09-20). Продвинутая линейная алгебра. Springer Science & Business Media. ISBN 978-0-387-72831-5.

[11] "Retraction - Encyclopedia of Mathematics". encyclopediaofmath.org . Получено 2021-08-11 .

[12] "Произведение семейства объектов в категории - Энциклопедия математики". encyclopediaofmath.org . Получено 2021-08-11 .