Биекция

| Функция |
|---|
| х ↦ f ( х ) |
| История концепции функции |
| Типы по домену и кодомумену |
| Классы/свойства |
| Конструкции |
| Обобщения |
| Список конкретных функций |
Биекция , биективная функция или взаимно однозначное соответствие между двумя математическими множествами — это функция , при которой каждый элемент второго множества ( области значений ) является образом ровно одного элемента первого множества ( области значений ). Эквивалентно, биекция — это отношение между двумя множествами, при котором каждый элемент любого множества сопоставляется ровно одному элементу другого множества.
Функция является биективной тогда и только тогда, когда она обратима; то есть функция является биективной тогда и только тогда, когда существует функция, обратная функции f , такая , что каждый из двух способов составления двух функций создает тождественную функцию : для каждого в и для каждого в
Например, умножение на два определяет биекцию целых чисел на четные числа , которая имеет деление на два в качестве своей обратной функции.
Функция является биективной тогда и только тогда, когда она является как инъективной (или взаимно-однозначной ) — что означает, что каждый элемент в кодомене отображается в из не более чем одного элемента домена — так и сюръективной (или на ) — что означает, что каждый элемент кодомена отображается в из по крайней мере одного элемента домена. Термин соответствие один-к-одному не следует путать с функцией один-к-одному , что означает инъективность, но не обязательно сюръективность.
Элементарная операция подсчета устанавливает биекцию из некоторого конечного множества на первые натуральные числа (1, 2, 3, ...) с точностью до числа элементов в подсчитанном множестве. Это приводит к тому, что два конечных множества имеют одинаковое число элементов тогда и только тогда, когда между ними существует биекция. В более общем смысле говорят, что два множества имеют одинаковое кардинальное число , если между ними существует биекция.
Биективная функция из множества в себя также называется перестановкой [ 1], а множество всех перестановок множества образует его симметрическую группу .
Некоторые биекции с дополнительными свойствами получили специальные названия, которые включают автоморфизмы , изоморфизмы , гомеоморфизмы , диффеоморфизмы , группы перестановок и большинство геометрических преобразований . Соответствия Галуа являются биекциями между множествами математических объектов , по-видимому, очень разной природы.
Определение
Для того чтобы бинарное отношение, соединяющее элементы множества X с элементами множества Y , было биекцией, должны выполняться четыре свойства:
- каждый элемент X должен быть сопряжен по крайней мере с одним элементом Y ,
- ни один элемент X не может быть сопряжен более чем с одним элементом Y ,
- каждый элемент Y должен быть сопряжен по крайней мере с одним элементом X , и
- ни один элемент Y не может быть сопряжен более чем с одним элементом X.
Удовлетворение свойств (1) и (2) означает, что спаривание является функцией с областью X. Чаще всего свойства (1) и (2) записываются в виде одного утверждения: Каждый элемент X спаривается ровно с одним элементом Y. Функции, удовлетворяющие свойству (3), называются « на Y » и называются сюръекциями (или сюръективными функциями ). Функции, удовлетворяющие свойству (4), называются « один-к-одному функциями » и называются инъекциями (или инъективными функциями ). [2] Согласно этой терминологии, биекция — это функция, которая является как сюръекцией, так и инъекцией, или, другими словами, биекция — это функция, которая является как «один-к-одному», так и «на». [3]
Примеры
Состав отбивающих в бейсбольной или крикетной команде
Рассмотрим состав отбивающих бейсбольной или крикетной команды (или любой список всех игроков любой спортивной команды, где каждый игрок занимает определенное место в составе). Набор X будет игроками команды (размером девять в случае бейсбола), а набор Y будет позициями в порядке отбивания (1-й, 2-й, 3-й и т. д.). «Сочетание» задается тем, какой игрок находится на какой позиции в этом порядке. Свойство (1) выполняется, поскольку каждый игрок находится где-то в списке. Свойство (2) выполняется, поскольку ни один игрок не отбивает на двух (или более) позициях в порядке. Свойство (3) говорит, что для каждой позиции в порядке есть некоторый игрок, отбивающий на этой позиции, а свойство (4) говорит, что два или более игроков никогда не отбивают на одной и той же позиции в списке.
Места и ученики в классе
В классе есть определенное количество мест. Группа студентов входит в комнату, и преподаватель просит их сесть. После быстрого осмотра комнаты преподаватель заявляет, что существует биекция между набором студентов и набором мест, где каждый студент связан с местом, на котором он сидит. Чтобы прийти к такому выводу, преподаватель наблюдал следующее:
- Каждый студент сидел на своем месте (никто не стоял),
- Ни один студент не сидел более чем на одном месте,
- На каждом месте кто-то сидел (пустых мест не было), и
- Ни на одном месте не сидело больше одного студента.
Преподаватель смог сделать вывод, что мест было столько же, сколько и учеников, не считая ни одного из комплектов.
Больше математических примеров
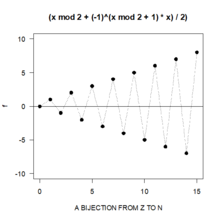
- Для любого множества X функция тождества 1 X : X → X , 1 X ( x ) = x является биекцией.
- Функция f : R → R , f ( x ) = 2 x + 1 является биекцией, поскольку для каждого y существует уникальный x = ( y − 1)/2 такой, что f ( x ) = y . В более общем смысле, любая линейная функция над действительными числами, f : R → R , f ( x ) = ax + b (где a не равно нулю) является биекцией. Каждое действительное число y получается из (или спаривается с) действительного числа x = ( y − b )/ a .
- Функция f : R → (−π/2, π/2), заданная как f ( x ) = arctan( x ), является биективной, поскольку каждое действительное число x сопряжено ровно с одним углом y в интервале (−π/2, π/2), так что tan( y ) = x (то есть y = arctan( x )). Если бы область значений (−π/2, π/2) была увеличена, чтобы включить целое число, кратное π/2, то эта функция больше не была бы сюръективной, поскольку нет действительного числа, которое могло бы быть сопряжено с кратным π/2 этой функцией arctan.
- Экспоненциальная функция , g : R → R , g ( x ) = e x , не является биективной: например, нет x в R такого, что g ( x ) = −1, показывая, что g не является онто (сюръективной). Однако, если область значений ограничена положительными действительными числами , то g будет биективной; ее обратная функция (см. ниже) является функцией натурального логарифма ln.
- Функция h : R → R + , h ( x ) = x 2 не является биективной: например, h (−1) = h (1) = 1, показывая, что h не является взаимно-однозначной (инъективной). Однако, если область ограничена , то h будет биективной; ее обратная функция — это положительная функция квадратного корня.
- По теореме Шредера–Бернштейна , если заданы любые два множества X и Y и две инъективные функции f : X → Y и g : Y → X , то существует биективная функция h : X → Y .
Обратные
Биекция f с областью определения X (обозначаемая как f : X → Y в функциональной нотации ) также определяет обратное отношение , начинающееся в Y и идущее к X (поворачивая стрелки). Процесс «поворота стрелок» для произвольной функции, в общем случае , не дает функцию, но свойства (3) и (4) биекции говорят, что это обратное отношение является функцией с областью определения Y. Более того, свойства (1) и (2) затем говорят, что эта обратная функция является сюръекцией и инъекцией, то есть обратная функция существует и также является биекцией. Функции, которые имеют обратные функции, называются обратимыми . Функция обратима тогда и только тогда, когда она является биекцией.
Выражаясь кратко в математической нотации, функция f : X → Y является биективной тогда и только тогда, когда она удовлетворяет условию
- для каждого y в Y существует уникальный x в X с y = f ( x ).
Продолжая пример с расстановкой игроков в бейсболе, определяемая функция принимает в качестве входных данных имя одного из игроков и выводит позицию этого игрока в порядке отбивания. Поскольку эта функция является биекцией, у нее есть обратная функция, которая принимает в качестве входных данных позицию в порядке отбивания и выводит игрока, который будет отбивать в этой позиции.
Состав

Композиция двух биекций f : X → Y и g : Y → Z является биекцией, обратная которой задается соотношением is .
Наоборот, если композиция двух функций биективна, то отсюда следует только, что f инъективна , а g сюръективна .
Мощность
Если X и Y являются конечными множествами , то существует биекция между двумя множествами X и Y тогда и только тогда, когда X и Y имеют одинаковое количество элементов. Действительно, в аксиоматической теории множеств это принимается как определение «одинакового количества элементов» ( равночисленности ), и обобщение этого определения на бесконечные множества приводит к концепции кардинального числа , способа различать различные размеры бесконечных множеств.
Характеристики
- Функция f : R → R является биективной тогда и только тогда, когда ее график пересекает каждую горизонтальную и вертикальную линию ровно один раз.
- Если X — множество, то биективные функции из X в себя вместе с операцией функциональной композиции (∘) образуют группу , симметрическую группу X , которая обозначается по-разному как S( X ), S X или X ! ( X factorial ).
- Биекции сохраняют мощности множеств: для подмножества A области с мощностью | A | и подмножества B области значений с мощностью | B | выполняются следующие равенства:
- | f ( A )| = | A | и | f −1 ( B )| = | B |.
- Если X и Y — конечные множества с одинаковой мощностью и f : X → Y , то следующие условия эквивалентны:
- Для конечного множества S существует биекция между множеством возможных полных упорядочений элементов и множеством биекций из S в S. То есть число перестановок элементов S совпадает с числом полных упорядочений этого множества, а именно, n !.
Теория категорий
Биекции — это в точности изоморфизмы в категории Set множеств и функций множеств. Однако биекции не всегда являются изоморфизмами для более сложных категорий. Например, в категории Grp групп морфизмы должны быть гомоморфизмами , поскольку они должны сохранять структуру группы, поэтому изоморфизмы являются групповыми изоморфизмами, которые являются биективными гомоморфизмами.
Обобщение на частичные функции
Понятие взаимно-однозначного соответствия обобщается на частичные функции , где они называются частичными биекциями , хотя от частичных биекций требуется только быть инъективными. Причина этого ослабления заключается в том, что (собственная) частичная функция уже не определена для части своей области определения; таким образом, нет убедительных причин ограничивать ее обратную функцию полной функцией , т.е. определенной всюду на своей области определения. Множество всех частичных биекций на заданном базовом множестве называется симметричной инверсной полугруппой . [4]
Другой способ определения того же понятия — сказать, что частичная биекция из A в B — это любое отношение R (которое оказывается частичной функцией) со свойством, что R является графиком биекции f : A′ → B′ , где A′ — подмножество A , а B′ — подмножество B . [5]
Когда частичная биекция находится на том же множестве, ее иногда называют частичным преобразованием один к одному . [6] Примером является преобразование Мёбиуса, просто определенное на комплексной плоскости, а не его завершение на расширенной комплексной плоскости. [7]
Галерея
Смотрите также
- Теорема Акса–Гротендика
- Биекция, инъекция и сюръекция
- Биективная нумерация
- Биективное доказательство
- Теория категорий
- Многозначная функция
Примечания
- ^ Холл 1959, стр. 3
- ^ Существуют также имена, связанные со свойствами (1) и (2). Отношение, которое удовлетворяет свойству (1), называется полным отношением , а отношение, удовлетворяющее (2), является однозначным отношением .
- ^ «Биекция, инъекция и сюръекция | Brilliant Math & Science Wiki». brilliant.org . Получено 7 декабря 2019 г. .
- ^ Кристофер Холлингс (16 июля 2014 г.). Математика через железный занавес: история алгебраической теории полугрупп. Американское математическое общество. стр. 251. ISBN 978-1-4704-1493-1.
- ^ Фрэнсис Борсе (1994). Справочник по категориальной алгебре: Том 2, Категории и структуры. Cambridge University Press. стр. 289. ISBN 978-0-521-44179-7.
- ^ Пьер А. Грийе (1995). Полугруппы: Введение в теорию структур. CRC Press. стр. 228. ISBN 978-0-8247-9662-4.
- ^ Джон Микин (2007). "Группы и полугруппы: связи и контрасты". В CM Campbell; MR Quick; EF Robertson; GC Smith (ред.). Группы St Andrews 2005 Том 2. Cambridge University Press. стр. 367. ISBN 978-0-521-69470-4.препринт, цитирующий Lawson, MV (1998). "Обратный моноид Мёбиуса". Журнал алгебры . 200 (2): 428–438. doi : 10.1006/jabr.1997.7242 .
Ссылки
Эта тема является базовой концепцией в теории множеств и может быть найдена в любом тексте, который включает введение в теорию множеств. Почти все тексты, которые имеют дело с введением в написание доказательств, будут включать раздел о теории множеств, поэтому тему можно найти в любом из них:
- Холл, Маршалл-младший (1959). Теория групп . Макмиллан.
- Вольф (1998). Доказательство, логика и гипотеза: набор инструментов математика . Фримен.
- Sundstrom (2003). Математическое обоснование: написание и доказательство . Prentice-Hall.
- Смит; Эгген; Сент-Андре (2006). Переход к высшей математике (6-е изд.) . Томсон (Брукс/Коул).
- Шумахер (1996). Глава нулевая: основные понятия абстрактной математики . Эддисон-Уэсли.
- О'Лири (2003). Структура доказательства: с логикой и теорией множеств . Prentice-Hall.
- Мораш. Мост к абстрактной математике . Random House.
- Мэддокс (2002). Математическое мышление и письмо . Harcourt/Academic Press.
- Лэй (2001). Анализ с введением в доказательство . Prentice Hall.
- Гилберт; Ванстоун (2005). Введение в математическое мышление . Пирсон Прентис-Холл.
- Флетчер; Пэтти. Основы высшей математики . PWS-Кент.
- Иглевич; Стойл. Введение в математическое мышление . Макмиллан.
- Девлин, Кит (2004). Множества, функции и логика: введение в абстрактную математику . Chapman & Hall/ CRC Press.
- D'Angelo; West (2000). Математическое мышление: решение проблем и доказательства . Prentice Hall.
- Купиллари (1989). Основы доказательств . Уодсворт. ISBN 9780534103200.
- Бонд. Введение в абстрактную математику . Брукс/Коул.
- Барнье; Фельдман (2000). Введение в высшую математику . Prentice Hall.
- Эш. Учебник абстрактной математики . MAA.
Внешние ссылки
- «Биекция», Энциклопедия математики , EMS Press , 2001 [1994]
- Вайсштейн, Эрик В. «Биекция». MathWorld .
- Самые ранние случаи использования некоторых слов из математики: статья об инъекции, сюръекции и биекции содержит историю инъекции и связанных с ней терминов.

















