Параболический отражатель


Параболический (или параболоидный или параболоидальный ) отражатель (или тарелка или зеркало ) — это отражающая поверхность , используемая для сбора или проецирования энергии, такой как свет , звук или радиоволны . Его форма является частью кругового параболоида , то есть поверхности, образованной параболой, вращающейся вокруг своей оси. Параболический отражатель преобразует входящую плоскую волну, распространяющуюся вдоль оси, в сферическую волну, сходящуюся к фокусу. И наоборот, сферическая волна, образованная точечным источником, помещенным в фокус, отражается в плоскую волну, распространяющуюся как коллимированный пучок вдоль оси.
Параболические отражатели используются для сбора энергии из удаленного источника (например, звуковых волн или входящего звездного света). Поскольку принципы отражения обратимы, параболические отражатели также могут использоваться для коллимации излучения из изотропного источника в параллельный пучок . [1] В оптике параболические зеркала используются для сбора света в отражательных телескопах и солнечных печах , а также для проецирования луча света в фонариках , прожекторах , сценических прожекторах и автомобильных фарах . В радио параболические антенны используются для излучения узкого пучка радиоволн для связи точка-точка в спутниковых антеннах и микроволновых ретрансляционных станциях, а также для обнаружения самолетов, кораблей и транспортных средств в радиолокационных установках. В акустике параболические микрофоны используются для записи далеких звуков, таких как крики птиц , в спортивных репортажах и для подслушивания частных разговоров в шпионаже и правоохранительных органах.
Теория
Строго говоря, трехмерная форма отражателя называется параболоидом . Парабола — это двумерная фигура. (Различие такое же, как между сферой и кругом.) Однако в неформальном языке слово парабола и связанное с ним прилагательное параболический часто используются вместо параболоида и параболоидного . [2]
Если парабола расположена в декартовых координатах с вершиной в начале координат и осью симметрии вдоль оси y, так что парабола ветвится вверх, ее уравнение имеет вид , где - ее фокусное расстояние. (См. " Парабола # В декартовой системе координат ".) Соответственно, размеры симметричной параболоидной тарелки связаны уравнением: , где - фокусное расстояние, - глубина тарелки (измеряется вдоль оси симметрии от вершины до плоскости обода), а - радиус тарелки от центра. Все единицы, используемые для радиуса, фокусной точки и глубины, должны быть одинаковыми. Если известны две из этих трех величин, это уравнение можно использовать для вычисления третьей.
Для нахождения диаметра тарелки, измеренного вдоль ее поверхности , требуется более сложный расчет . Иногда его называют «линейным диаметром», и он равен диаметру плоского круглого листа материала, обычно металла, который имеет правильный размер для резки и гибки для изготовления тарелки. Для расчета полезны два промежуточных результата: (или эквивалент: ) и , где F , D , и R определены, как указано выше. Диаметр тарелки, измеренный вдоль поверхности, затем определяется по формуле: , где означает натуральный логарифм x , т. е. его логарифм по основанию « e » .
Объем тарелки определяется по формуле , где символы определены так же, как указано выше. Это можно сравнить с формулами для объемов цилиндра, полушария , где и конуса — площадь апертуры тарелки, площадь, заключенная в ободок, которая пропорциональна количеству солнечного света, которое может перехватить отражающая тарелка. Площадь вогнутой поверхности тарелки можно найти с помощью формулы площади для поверхности вращения, которая дает . обеспечивая . Доля света, отраженного тарелкой от источника света в фокусе, определяется по формуле , где и определяются так же, как указано выше.
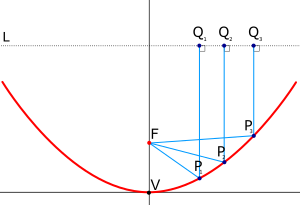
Параболический отражатель функционирует благодаря геометрическим свойствам параболоидальной формы: любой входящий луч , параллельный оси тарелки, будет отражаться в центральную точку, или « фокус ». (Для геометрического доказательства нажмите здесь .) Поскольку многие типы энергии могут отражаться таким образом, параболические отражатели могут использоваться для сбора и концентрации энергии, поступающей в отражатель под определенным углом. Аналогично, энергия, излучаемая из фокуса в тарелку, может передаваться наружу в виде луча, параллельного оси тарелки.
В отличие от сферических рефлекторов , которые страдают от сферической аберрации , которая становится сильнее по мере увеличения отношения диаметра луча к фокусному расстоянию, параболические рефлекторы могут быть сделаны для размещения лучей любой ширины. Однако, если входящий луч образует ненулевой угол с осью (или если излучающий точечный источник не находится в фокусе), параболические рефлекторы страдают от аберрации, называемой комой . Это в первую очередь представляет интерес для телескопов, поскольку большинство других приложений не требуют резкого разрешения вне оси параболы.
Точность, с которой параболическая тарелка должна быть сделана для того, чтобы хорошо фокусировать энергию, зависит от длины волны энергии. Если тарелка неправильная на четверть длины волны, то отраженная энергия будет неправильной на половину длины волны, что означает, что она будет деструктивно мешать энергии, которая была правильно отражена от другой части тарелки. Чтобы предотвратить это, тарелка должна быть сделана правильно с точностью около 1/20 длины волны. Диапазон длин волн видимого света составляет от 400 до 700 нанометров (нм), поэтому для того, чтобы хорошо сфокусировать весь видимый свет, отражатель должен быть точным с точностью до 20 нм. Для сравнения, диаметр человеческого волоса обычно составляет около 50 000 нм, поэтому требуемая точность для отражателя, чтобы сфокусировать видимый свет, примерно в 2500 раз меньше диаметра волоса. Например, дефект в зеркале космического телескопа Хаббл (слишком плоское примерно на 2200 нм по периметру) вызывал серьезную сферическую аберрацию, пока ее не исправили с помощью COSTAR . [3]
Микроволны, используемые, например, для передачи сигналов спутникового телевидения, имеют длину волны порядка десяти миллиметров, поэтому антенны, фокусирующие эти волны, могут ошибаться примерно на полмиллиметра и все равно работать хорошо.
Вариации
Фокусно-сбалансированный рефлектор

Иногда бывает полезно, если центр масс отражающей тарелки совпадает с ее фокусом . Это позволяет легко поворачивать ее так, чтобы ее можно было направить на движущийся источник света, например, Солнце в небе, в то время как ее фокус, где находится цель, неподвижен. Тарелка вращается вокруг осей, которые проходят через фокус и вокруг которых она сбалансирована. Если тарелка симметрична и сделана из однородного материала постоянной толщины, и если F представляет собой фокусное расстояние параболоида, это «фокусно-сбалансированное» состояние возникает, если глубина тарелки, измеренная вдоль оси параболоида от вершины до плоскости обода тарелки, составляет 1,8478 F . Радиус обода равен 2,7187 F . [a] Угловой радиус обода, видимый из фокусной точки, составляет 72,68 градуса.
Рефлектор Шеффлера
Конфигурация с балансировкой фокуса (см. выше) требует, чтобы глубина тарелки рефлектора была больше ее фокусного расстояния, поэтому фокус находится внутри тарелки. Это может привести к тому, что фокус будет труднодоступным. Альтернативный подход иллюстрируется рефлектором Шеффлера , названным в честь его изобретателя Вольфганга Шеффлера . Это параболоидное зеркало, которое вращается вокруг осей, проходящих через его центр масс, но это не совпадает с фокусом, который находится снаружи тарелки. Если бы рефлектор был жестким параболоидом, фокус перемещался бы по мере поворота тарелки. Чтобы избежать этого, рефлектор гибкий и изгибается при вращении, чтобы удерживать фокус неподвижным. В идеале рефлектор должен быть точно параболоидным все время. На практике этого невозможно достичь в точности, поэтому рефлектор Шеффлера не подходит для целей, требующих высокой точности. Он используется в таких приложениях, как солнечная кулинария , где солнечный свет должен быть сфокусирован достаточно хорошо, чтобы попасть на кастрюлю, но не в точную точку. [4]
Внеосевые отражатели

Круговой параболоид теоретически не ограничен по размеру. Любой практический отражатель использует только его сегмент. Часто сегмент включает вершину параболоида, где его кривизна наибольшая, и где ось симметрии пересекает параболоид. Однако, если отражатель используется для фокусировки входящей энергии на приемник, тень приемника падает на вершину параболоида, которая является частью отражателя, поэтому часть отражателя тратится впустую. Этого можно избежать, сделав отражатель из сегмента параболоида, который смещен относительно вершины и оси симметрии. Весь отражатель получает энергию, которая затем фокусируется на приемнике. Это часто делается, например, в спутниковых телевизионных приемных антеннах, а также в некоторых типах астрономических телескопов ( например , телескоп Грин-Бэнк , космический телескоп Джеймса Уэбба ).
Точные внеосевые отражатели для использования в солнечных печах и других некритических приложениях можно изготовить довольно просто, используя вращающуюся печь , в которой контейнер с расплавленным стеклом смещен относительно оси вращения. Для изготовления менее точных, подходящих в качестве спутниковых антенн, форма проектируется на компьютере, затем несколько тарелок штампуются из листового металла.
Внеосевые рефлекторы, направляющиеся из средних широт к геостационарному телевизионному спутнику где-то над экватором, стоят круче, чем коаксиальный рефлектор. Эффект в том, что рычаг, удерживающий тарелку, может быть короче, и снег имеет тенденцию меньше накапливаться в (нижней части) тарелки.

История
Принцип параболических отражателей известен со времен классической античности , когда математик Диокл описал их в своей книге «О зажигательных зеркалах» и доказал, что они фокусируют параллельный луч в точку. [5] Архимед в третьем веке до н. э. изучал параболоиды в рамках своего исследования гидростатического равновесия , [6] и утверждалось , что он использовал отражатели, чтобы поджечь римский флот во время осады Сиракуз . [7] Однако это кажется маловероятным, поскольку это утверждение не появляется в источниках до II века н. э., и Диокл не упоминает его в своей книге. [8] Параболические зеркала и отражатели также широко изучались физиком Роджером Бэконом в 13 веке н. э. [9] Джеймс Грегори в своей книге 1663 года Optica Promota (1663) указал, что рефлекторный телескоп с параболическим зеркалом исправит сферическую аберрацию , а также хроматическую аберрацию, наблюдаемую в рефракторных телескопах . Конструкция, которую он придумал, носит его имя: « Грегорианский телескоп »; но, по его собственному признанию, у Грегори не было практических навыков, и он не мог найти оптика, способного фактически построить его. [10] Исаак Ньютон знал о свойствах параболических зеркал, но выбрал сферическую форму для своего ньютоновского телескопического зеркала, чтобы упростить конструкцию. [11] Маяки также обычно использовали параболические зеркала для коллимации точки света от фонаря в луч, прежде чем их заменили более эффективные линзы Френеля в 19 веке. В 1888 году Генрих Герц , немецкий физик, построил первую в мире параболическую рефлекторную антенну. [12]
Приложения

Наиболее распространенными современными применениями параболического рефлектора являются спутниковые антенны , рефлекторные телескопы , радиотелескопы , параболические микрофоны , солнечные плиты и многие осветительные приборы, такие как прожекторы , автомобильные фары , лампы PAR и корпуса светодиодов. [14]

Олимпийский огонь традиционно зажигается в Олимпии, Греция , с помощью параболического отражателя, концентрирующего солнечный свет , а затем транспортируется к месту проведения Игр. Параболические зеркала являются одной из многих форм зажигательного стекла .
Параболические отражатели популярны для создания оптических иллюзий . Они состоят из двух противостоящих параболических зеркал с отверстием в центре верхнего зеркала. Когда объект помещается на нижнее зеркало, зеркала создают реальное изображение , которое является практически идентичной копией оригинала, который появляется в отверстии. Качество изображения зависит от точности оптики. Некоторые такие иллюзии изготавливаются с допусками в миллионные доли дюйма.
Параболический рефлектор, направленный вверх, может быть сформирован вращением отражающей жидкости, например ртути, вокруг вертикальной оси. Это делает возможным жидкозеркальный телескоп . Та же техника используется во вращающихся печах для изготовления твердых рефлекторов.
Параболические рефлекторы также являются популярной альтернативой для увеличения мощности беспроводного сигнала. Даже с простыми рефлекторами пользователи сообщали о 3 дБ и более приросте. [15] [16]
Смотрите также
- Джон Д. Краус
- Телескоп с жидкостным зеркалом , параболоиды, полученные вращением
- Параболическая антенна
- Параболический желоб
- Солнечная печь
- Тороидальный отражатель
Сноски
- ^ Близость этого числа к значению «e», основанию натуральных логарифмов, является всего лишь случайным совпадением, но оно представляет собой полезный мнемонический прием.
Ссылки
- ^ Фицпатрик, Ричард (2007-07-14). "Сферические зеркала". Farside.ph.utexas.edu . Получено 2012-11-08 .
- ^ «3D-печать с использованием сегментированной параболической отражательной изогнутой антенны миллиметрового диапазона 60 ГГц».
- ^ "Servicing Mission 1". NASA. Архивировано из оригинала 20 апреля 2008 года . Получено 26 апреля 2008 года .
- ^ Администратор. «Рефлектор Шеффлера». www.solare-bruecke.org .
- ↑ стр. 162–164, «Коника» Аполлония Пергского: текст, контекст, подтекст , Майкл Н. Фрид и Сабетай Унгуру , Brill, 2001, ISBN 90-04-11977-9 .
- ↑ стр. 73–74, Забытая революция: как зародилась наука в 300 г. до н. э. и почему ее пришлось возродить , Лучио Руссо, Birkhäuser, 2004, ISBN 3-540-20068-1 .
- ^ "Оружие Архимеда". Журнал Time . 26 ноября 1973 г. Архивировано из оригинала 12 октября 2007 г. Получено 12 августа 2007 г.
- ↑ стр. 72, Геометрия зажигательных зеркал в античности, Уилбур Кнорр , Isis 74 #1 (март 1983 г.), стр. 53–73, doi :10.1086/353176.
- ↑ С. 465, 468, 469, Пионер анакластики: Ибн Сахл о сжигании зеркал и линз, Рошди Рашед, Isis , 81 , № 3 (сентябрь 1990 г.), с. 464–491, doi :10.1086/355456.
- ^ Чемберс, Роберт (1875). Биографический словарь выдающихся шотландцев. Оксфордский университет. С. 175.
- ^ Маклин, Ян С. (2008-07-29). Электронная визуализация в астрономии: детекторы и приборы. ISBN 9783540765820. Получено 2012-11-08 .
- ^ «Предыстория радиоастрономии». www.nrao.edu .
- ^ "ALMA удваивает свою мощность в новой фазе более продвинутых наблюдений". Объявление ESO . Получено 11 января 2013 г.
- ^ Фицпатрик, Ричард (2007-07-14). "Сферические зеркала". Farside.ph.utexas.edu . Получено 2012-11-08 .
- ^ "Parabolic Reflector Free WiFi Booster". Обновление "Сделай сам" по беспроводным антеннам и центр ресурсов Wi-Fi | Вопросы и ответы по беспроводному WiFi . Binarywolf.com. 2009-08-26. Архивировано из оригинала 2019-06-09 . Получено 2012-11-08 .
- ^ "Слайд-шоу: Wi-Fi Shootout в пустыне". Wired. 2004-08-03 . Получено 2012-11-08 .
Внешние ссылки
- Демонстрация параболического рефлектора на Java
- Параболические рефлекторные антенны www.antenna-theory.com
- Анимации, демонстрирующие параболическое зеркало от QED
- Изготовление больших параболоидных рефлекторов с использованием плоских сегментов























