Октаграмма
| Правильная октаграмма | |
|---|---|
 Правильная октаграмма | |
| Тип | Правильный звездчатый многоугольник |
| Ребра и вершины | 8 |
| Символ Шлефли | {8/3} т{4/3} |
| Диаграммы Кокстера–Дынкина |       |
| Группа симметрии | Двугранный (D 8 ) |
| Внутренний угол ( градусы ) | 45° |
| Характеристики | звезда , циклическая , равносторонняя , изогональная , изотоксальная |
| Двойной полигон | себя |
| Звездные многоугольники |
|---|
В геометрии октаграмма — это восьмиугольный звездчатый многоугольник .
Название октаграмма объединяет греческий префикс числа , окта- , с греческим суффиксом -грам . Суффикс -грам происходит от γραμμή ( grammḗ ), что означает «линия». [1]
Деталь
В общем случае октаграмма — это любой самопересекающийся восьмиугольник ( многоугольник с восемью сторонами ).
Правильная октаграмма обозначается символом Шлефли {8/3}, что означает восьмиконечную звезду, соединенную каждой третьей точкой.
Вариации
Эти вариации имеют нижнюю двугранную симметрию Dih 4 :
 Узкий  Широкий (поворот на 45 градусов) |   Изотоксальный |  Старый флаг Чили содержал эту геометрию восьмиугольной звезды со срезанными краями ( Гуньельве ). |  Правильная восьмиугольная звезда очень популярна как символ гребных клубов Кельнской низменности , как видно на флаге Кельнской ассоциации гребцов . |  Геометрию можно настроить так, чтобы три ребра пересекались в одной точке, как символ Аусеклиса. |  Восьмилучевую розу компаса можно рассматривать как восьмиконечную звезду с 4 основными и 4 второстепенными лучами. |
Символ Руб эль Хизб — это глиф Unicode ۞ в позиции U+06DE.
Как квазиусеченный квадрат
Более глубокие усечения квадрата могут производить изогональные (вершинно-транзитивные) промежуточные формы звездного многоугольника с равноотстоящими вершинами и двумя длинами ребер. Усеченный квадрат — это восьмиугольник, t{4}={8}. Квазиусеченный квадрат, инвертированный как {4/3}, — это октаграмма, t{4/3}={8/3}. [2]
Равномерный звездчатый многогранник, звездчатый усеченный гексаэдр , t'{4,3}=t{4/3,3} имеет грани октаграммы, построенные из куба таким образом. По этой причине его можно рассматривать как трехмерный аналог октаграммы.
| Обычный | Квазирегулярный | Изогональный | Квазирегулярный |
|---|---|---|---|
 {4} |  т{4}={8} |  | 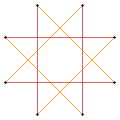 т'{4}=т{4/3}={8/3} |
| Обычный | Униформа | Изогональный | Униформа |
 {4,3} |  т{4,3} |  |  т'{4,3}=т{4/3,3} |
Другой трехмерной версией октаграммы является невыпуклый большой ромбокубооктаэдр (квазиромбокубооктаэдр), который можно рассматривать как квазиконусный (квазирасширенный) куб, t 0,2 {4/3,3}.
Соединения звездчатых многоугольников
Существуют две правильные октаграммические звездные фигуры (соединения) формы {8/k}, первая из которых построена как два квадрата {8/2}=2{4}, а вторая как четыре вырожденных двуугольника , {8/4}=4{2}. Существуют и другие изогональные и изотоксальные соединения, включая прямоугольные и ромбические формы.
| Обычный | Изогональный | Изотоксальный | ||
|---|---|---|---|---|
.svg/1280px-Regular_star_figure_2(4,1).svg.png) а{8}={8/2}=2{4} | .svg/1280px-Regular_star_figure_4(2,1).svg.png) {8/4}=4{2} |  |  |  |
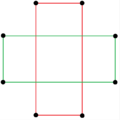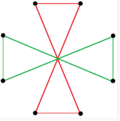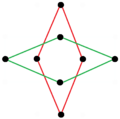{8/2} или 2{4}, как диаграммы Коксетера +, можно рассматривать как двумерный эквивалент трехмерного соединения куба и октаэдра ,
+, 4D соединение тессеракта и 16-ячеечной структуры,+и 5D соединение 5-куба и 5-ортоплекса ; то есть соединение n-куба и кросс-политопа в их соответствующих дуальных положениях.
Другие представления восьмиугольной звезды
Восьмиугольную звезду можно рассматривать как вогнутый гексадекагон , внутренняя пересекающаяся геометрия которого стерта. Ее также можно рассечь радиальными линиями.
| звездный многоугольник | Вогнутый | Центральные диссекции | ||
|---|---|---|---|---|
 Соединение 2{4} |  |8/2| |  |  |  |
 Регулярный {8/3} |  |8/3| |  |  |  |
 Изогональный |  |  |  |  |
 Изотоксальный |  |  |  |  |
Другие применения
_Commissioning_Image_(jupiter-hi-res-rings).tiff/lossless-page1-1280px-Jupiter%E2%80%99s_Rings_And_Moons_(NIRCam)_Commissioning_Image_(jupiter-hi-res-rings).tiff.png)
- Восьмиконечные дифракционные пики на изображениях звезд, полученных с помощью космического телескопа Джеймса Уэбба, возникают из-за дифракции , вызванной шестиугольной формой секций зеркала и распорок, удерживающих вторичное зеркало. [3]
- Используется в качестве условного обозначения или звезды для идентификатора Рождественской станции ABS-CBN 2010 года Ngayong Pasko Magninning Ang Pilipino ( букв. « В это Рождество филиппинцы будут сиять » ) из-за использования солнца на филиппинском флаге , что делает ее также песней на тему национализма и патриотизма, помимо рождественской песни.
Смотрите также
.svg){kind=link}
.svg){kind=link}
- Использование
- Руб эль Хизб – исламский персонаж
- звезда сельджуков
- Шамса
- Звезда Иштар – символ древней шумерской богини Инанны и ее восточносемитской аналогии Иштар и римской Венеры .
- Сешат – иероглиф этой древнеегипетской богини изображает цветок с семью лепестками, образующий со стеблем восьмиугольник.
- Звезда Лакшми – индийский персонаж
- Сурья Маджапахит – использовался во времена Маджапахита в Индонезии для обозначения индуистских богов сторон света.
- Компасная роза – используется в компасах для обозначения сторон света для восьми главных ветров.
- Аусеклис – использование латышами правильной октаграммы
- Гунельве — изображение Венеры в иконографии мапуче .
- Selburose – использование правильной восьмиугольной формы в норвежском дизайне
- Уту – древний месопотамский божественный символ и символ бога Солнца
- Звезды в целом
- Другие
Ссылки
- ^ «Генри Джордж Лидделл, Роберт Скотт, Греко-английский лексикон, γραμμή» . www.perseus.tufts.edu . Проверено 31 октября 2024 г.
- ^ Более светлая сторона математики: Труды конференции памяти Эжена Стренса по занимательной математике и ее истории, (1994), Метаморфозы многоугольников , Бранко Грюнбаум
- ^ Лоуренс, Пит (13 сентября 2022 г.). «Почему все звезды имеют 8 точек на снимках Джеймса Уэбба? Объясняет астроном». Журнал BBC Science Focus . Получено 1 марта 2023 г.
- Грюнбаум, Б. и GC Шепард; Мозаики и узоры , Нью-Йорк: WH Freeman & Co., (1987), ISBN 0-7167-1193-1 .
- Грюнбаум, Б.; Многогранники с полыми гранями, Труды конференции НАТО-АСИ по многогранникам ... и т. д. (Торонто, 1993) , под ред. Т. Бистрицки и др., Kluwer Academic (1994) стр. 43–70.
- Джон Х. Конвей , Хайди Бергиел, Хаим Гудман-Штраус, Симметрии вещей 2008, ISBN 978-1-56881-220-5 (Глава 26. стр. 404: Правильные звездчатые многогранники, измерение 2)
Внешние ссылки
- Вайсштейн, Эрик В. «Октаграмма». MathWorld .
